Тема Ряды динамики Все явления изменяются во времени, вместе с этим изменяются и их количественные (в частности, статистические) показатели

Вид материала

Документы

Содержание Тема 8. Индексы 8.1. Индивидуальные и общие индексы 8.2. Агрегатные индексы

Подобный материал:

• Ряды динамики, 73.43kb.
• Лекция №6 «Ряды динамики», 196.16kb.
• Внешняя трудовая миграция, 178.75kb.
• Задачи и виды группировок Статистические ряды распределения Абсолютные показатели, 18.57kb.
• Содержание Обобщенная модель управления запасами, 372.31kb.
• 1 измерение температуры. Шкалы температур. Классификация методов и приборов температурой, 948.25kb.
• Конспект лекций по дисциплине Статистика Модуль, 213.5kb.
• Кыргызско-турецкий университет «манас» силлабус, 108.52kb.
• Анализ работы районного методического кабинета управления образования администрации, 1331.86kb.
• Методика лечебного голодания по Бухингеру, 67.58kb.

^

Тема 8. Индексы

Индекс – это относительная величина, характеризующая изменение уровня статистического показателя во времени, в пространстве, по сравнению с какой-либо нормой или стандартом.

Наиболее распространенными являются индексы цен, объема продаж (производства), товарооборота, себестоимости, индексы динамики курсов ценных бумаг и др.
^

8.1. Индивидуальные и общие индексы

Индивидуальный индекс – это отношение, характеризующее изменение отдельного показателя по сравнению с базисным уровнем.

П
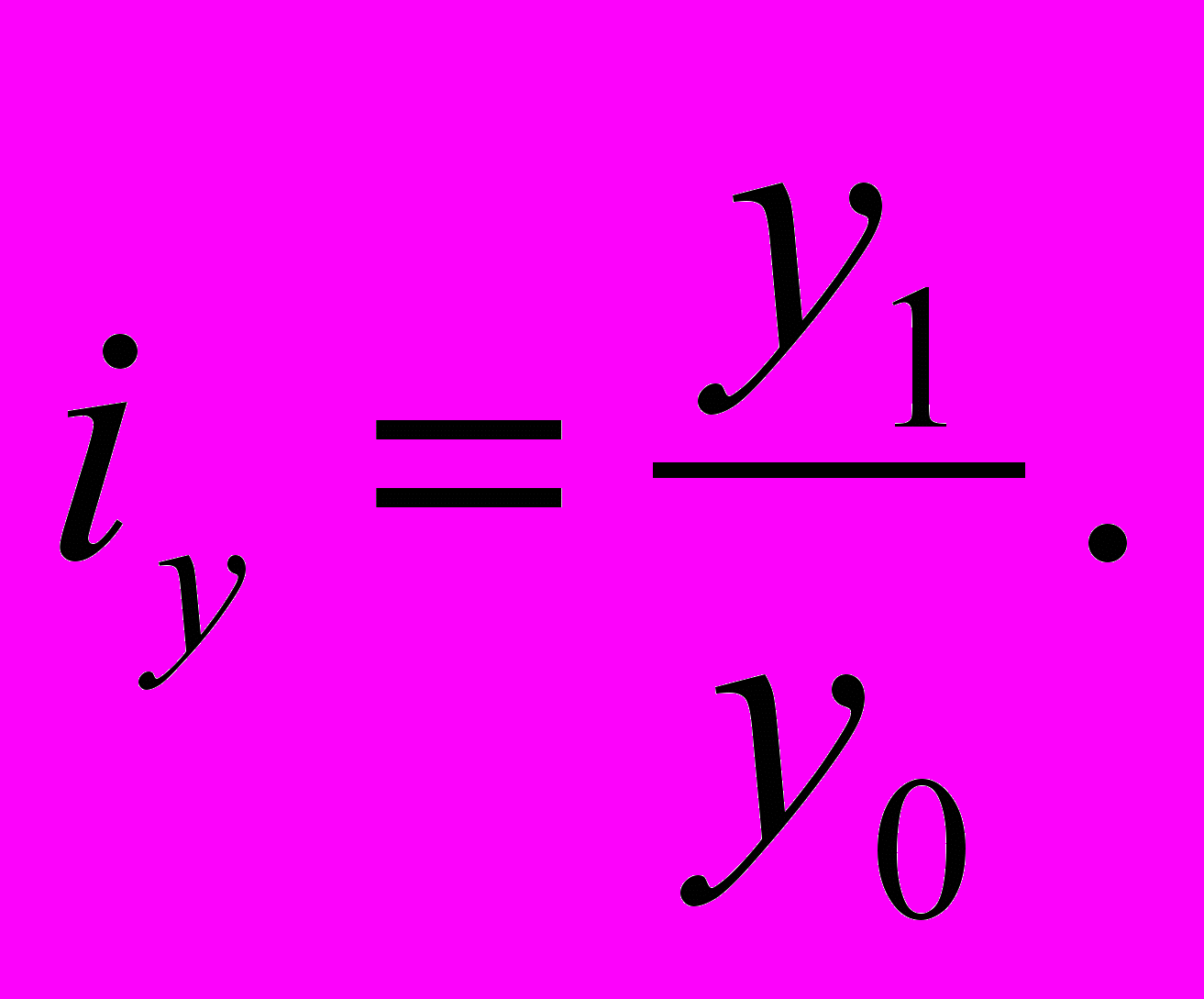
усть 0 – подстрочный символ базисного уровня, 1 – символ текущего уровня (или фактического, отчетного уровня), тогда у₀ – базисный уровень показателя, у₁ – отчетный уровень. Индивидуальный индекс показателя у равен

Н
апример, если р_0,1 – цены на определенный товар соответственно в базовый и отчетный периоды, то индивидуальный индекс цен

А
налогично, обозначая q_0,1 – объемы реализованного товара в базовый и отчетный периоды, получим индивидуальный индекс объема реализации

Очевидно, произведение введенных выше индексов дает индивидуальный индекс товарооборота

Д
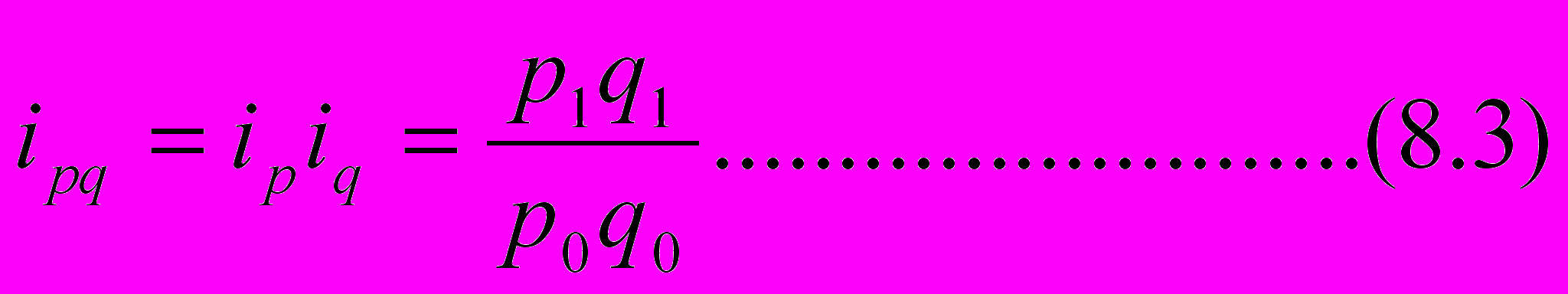
ругие часто встречающиеся индексы:

• индекс себестоимости i_z=z_1/z₀;
  
• индекс трудозатрат i_t=t₁/t₀;
  

• индекс энергозатрат i_e=e₁/e₀.
  

Если символы 0 и 1 обозначают временные интервалы, то индексы совпадают с базисными темпами роста (тема 7). В других случаях индексы дают сравнительную характеристику, например, региональных показателей. Скажем, индекс энергозатрат на производство в Украине по сравнению с Японией можно оценить величиной 1,6. Это несомненное свидетельство нашего богатства и расточительности!

Общий индекс – это относительная величина изменения показателя, определяемого для разнородных элементов после введения единой меры. Очень часто такой мерой в экономике является денежная единица. Различные товары, например, можно интегрировать после введения товарооборота как единого денежного эквивалента.


Пример 8.1. В 1997-1998 гг. показатели цен, объема реализации и товарооборота по двум группам товаров – телевизорам (ТВ) и микроволновым печам (МВП) сведены в таблицу 8.1


Таблица 8.1

Товар	Цена, т. грн.		Объем		товарооборот, т. грн.
	p0	p1	q0	q1	p0q0	p1q1	p0q1
TB	0,6	0,5	1000	1200	600	600	720
МВП	0,4	0,3	500	600	200	180	240
					800	780	960

О
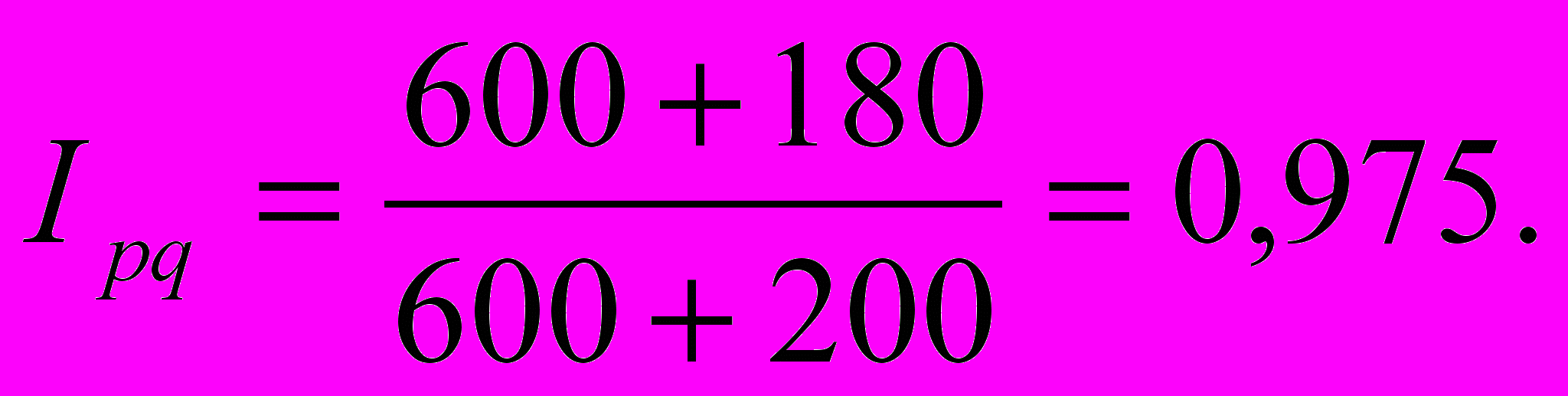
бщий индекс товарооборота здесь определяется как

Суммирование в этой формуле осуществляется по столбцам товарооборотов. Величина I_pq также называется общим агрегатным индексом товарооборота. Кроме них, бывают общие индексы средних величин (см.п. 8.5)
^

8.2. Агрегатные индексы

Агрегатные индексы являются наиболее распространенной разновидностью общих индексов. Общий индекс называется агрегатным, если он рассчитывается с помощью сумм произведений показателей (агрегатов), приведенных к эквивалентной мере. Обычно один из показателей является количественным (объемным, взвешивающим), другой – качественным. В приведенном выше примере р (цена) – качественный показатель, q – количественный,

pq – товарооборот как эквивалентная денежная мера. Сравнение товарооборота в отчетном и базовом периодах и с интегрированием разнородных товаров можно производить с помощью агрегатного и
ндекса товарооборота

В
озникает вопрос, можно ли произвести декомпозицию факторов (цены и объема продаж), влияющих на общий результат – товарооборот. Оказывается, это несложно сделать, помножив и разделив (8.4) на одну и ту же свертку и выделив сомножители

г

де

агрегатный индекс цен, и

• а
  грегатный индекс объема реализации. Как видно из (8.6), агрегатный индекс цены (качественного показателя) определяется при фиксированном количественном показателе q₁ в отчетном периоде, а агрегатный индекс (8.7) объема реализации – при фиксированном качественном показателе р₀ в базисном периоде. Разумеется, такой выбор фиксированных параметров является условным, но общепринятым, хотя можно было бы принять обратные периоды и изменить определения (8.6) и (8.7).
  

Пример 8.2. Определить агрегатные индексы цен и объема реализации для данных примера 8.1.

И
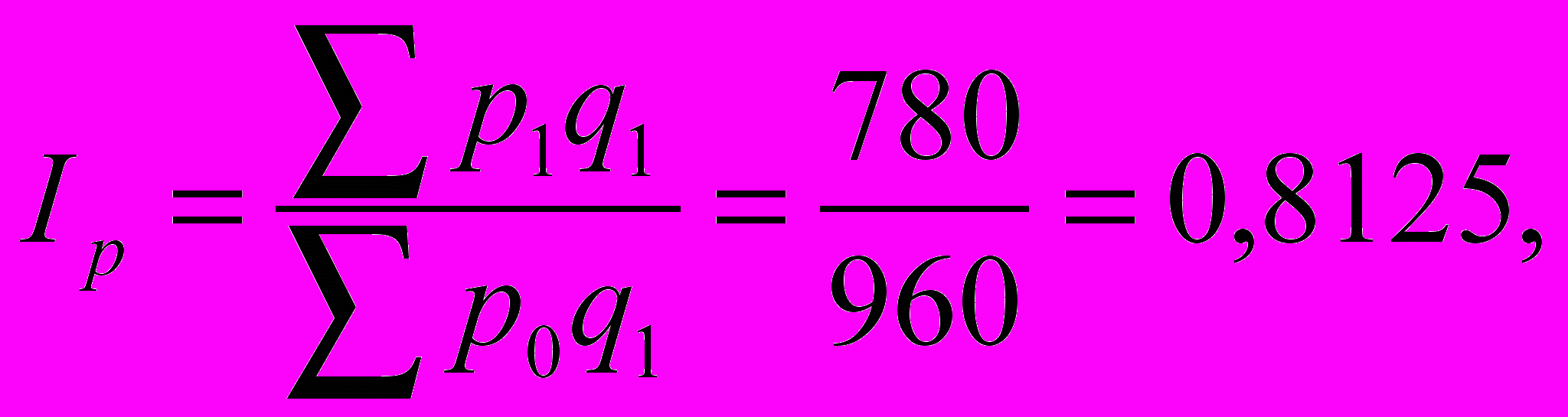
сходные данные для расчета дают последние столбцы и строки таблицы 8.1. Согласно (8.6), (8.7)


В
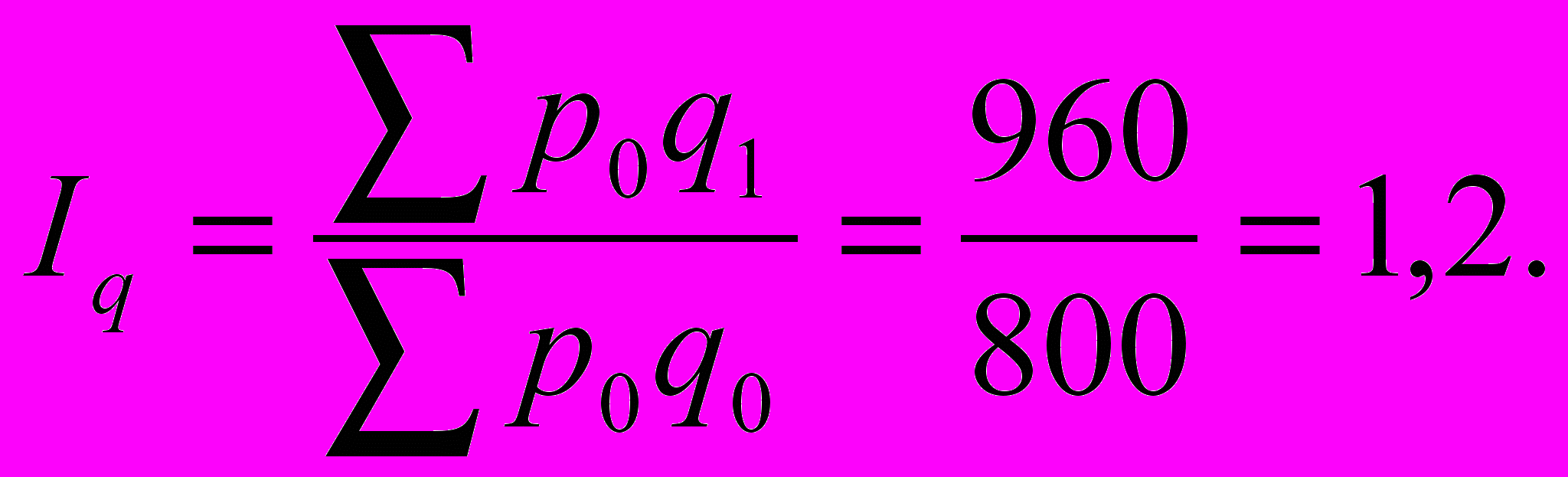
ывод: несмотря на существенное снижение цен (с индексом 0,8125) товарооборот ТВ и МВП почти не сократился (индекс 0,975) в связи с увеличением объема продаж на 20% (или в 1,2 раза).

Таким образом, агрегатные индексы I_p, I_q позволяют судить, как составляющие факторы (цены и объемы продаж) влияют на общий товарооборот. Это помогает делать обоснованные выводы и принимать верные экономические решения.