Тема Ряды динамики Все явления изменяются во времени, вместе с этим изменяются и их количественные (в частности, статистические) показатели

Вид материала

Документы

Содержание 8.3. Расчет агрегатных индексов путем усреднения индивидуальных 8.4. Факторный анализ 8.5. Общий индекс средних величин Себестоимость, грн./шт. Индекс объема Затраты труда на 1 изд,час

Подобный материал:

• Ряды динамики, 73.43kb.
• Лекция №6 «Ряды динамики», 196.16kb.
• Внешняя трудовая миграция, 178.75kb.
• Задачи и виды группировок Статистические ряды распределения Абсолютные показатели, 18.57kb.
• Содержание Обобщенная модель управления запасами, 372.31kb.
• 1 измерение температуры. Шкалы температур. Классификация методов и приборов температурой, 948.25kb.
• Конспект лекций по дисциплине Статистика Модуль, 213.5kb.
• Кыргызско-турецкий университет «манас» силлабус, 108.52kb.
• Анализ работы районного методического кабинета управления образования администрации, 1331.86kb.
• Методика лечебного голодания по Бухингеру, 67.58kb.

^

8.3. Расчет агрегатных индексов путем усреднения индивидуальных

И
зменив форму записи агрегатных индексов (8.6), (8.7), их можно выразить через среднее гармоническое и среднее арифметическое индивидуальных индексов. Действительно, из (8.1), (8.2) имеем

Подставляя эти выражения в (8.6), (8.7), получим

П

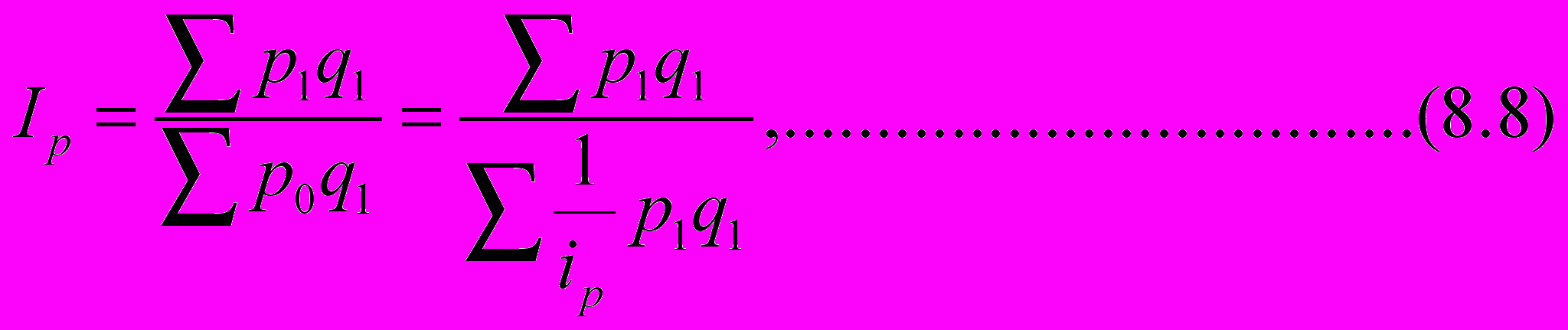
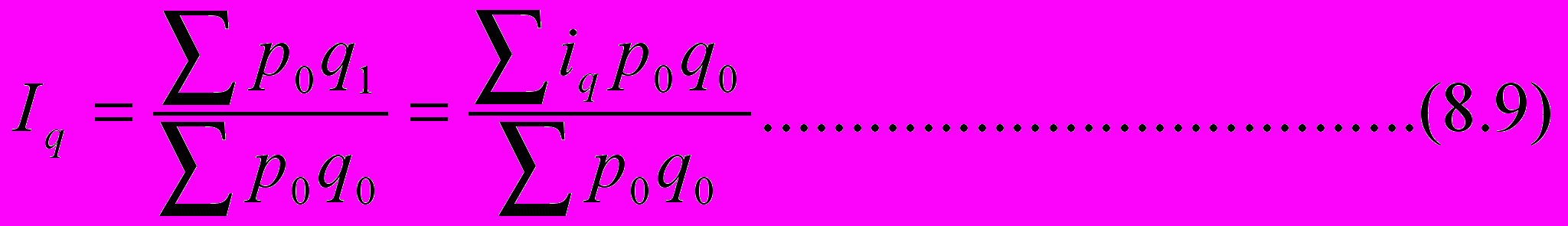
равая часть (8.8) является не чем иным, как средним гармоническим индивидуального индекса цен с усреднением по товарооборотам в отчетный период. Агрегатный индекс объема реализации (8.9) выражается уже как среднее арифметическое индивидуального индекса объема с усреднением в базовый период.


П
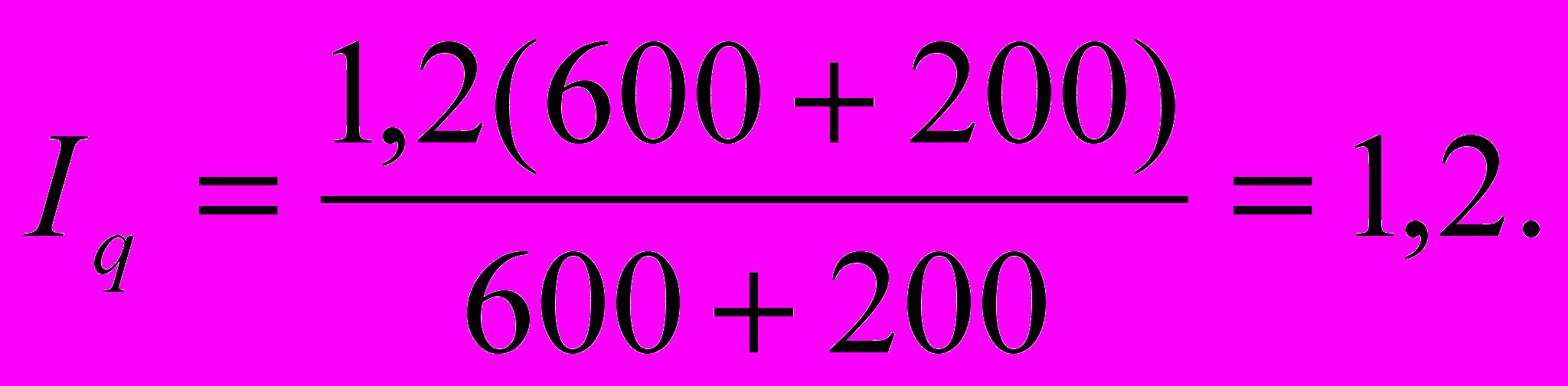
ример 8.3. Определим агрегатный индекс объема реализации по (8.9) с использованием данных примера 8.1. Индивидуальные индексы объема реализации ТВ и МВП одинаковы и равны i_q=q₁/q₀=1,2. Пользуясь столбцом p₀q₀ таблицы 8.1, получим

Естественно, результат тот же, что и по формуле (8.7).

Формулы усреднения удобны в тех случаях, когда известны индивидуальные индексы и данные за один период.
^

8.4. Факторный анализ

Часто производится параллельный расчет как относительных темпов роста (индексов), так и абсолютных приростов, которые на примере товарооборота выражаются в денежных единицах и потому важны. Такой параллельный расчет называют факторным анализом. Мы рассмотрим его на том же примере 8.1.

Если для индексов определяются отношения суммарных товарооборотов, то для абсолютных приростов из значений сумм в числителях вычитаются значения сумм в знаменателях, а произведения в индексах преобразуются в сумму для приростов. Итак, по данным табл.8.1 и
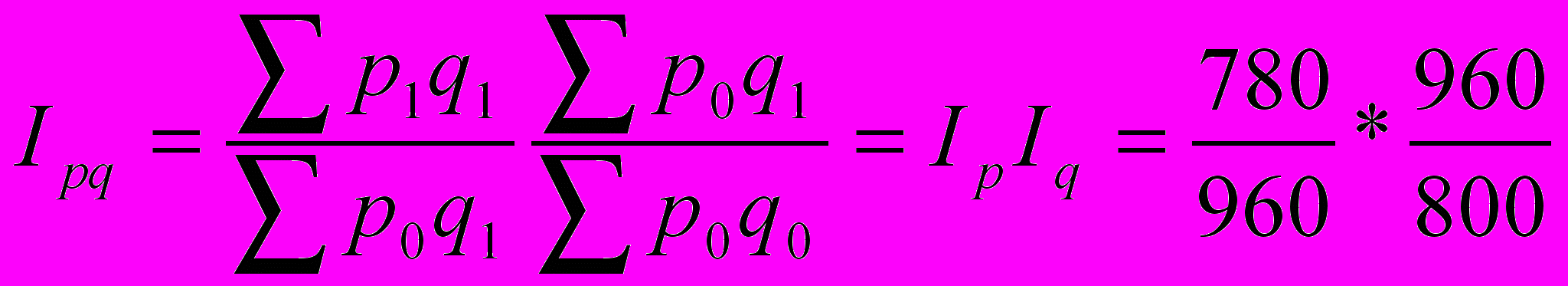
(8.5)

Тогда абсолютные приросты товарооборота за счет индексов цен и объема





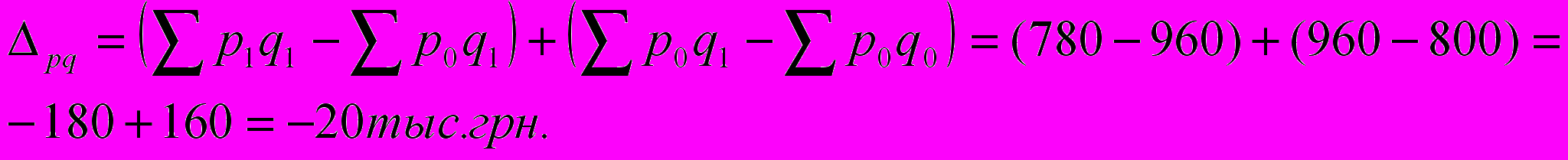
Отсюда нетрудно заключить, что за счет снижения цен товарооборот упал на 180 тыс. грн., но потери почти удалось компенсировать приростом товарооборота за счет объема продаж на 160 тыс.грн. В целом товарооборот в 1998 г снизился на 20 тыс.грн. по сравнению с 1997 г.

В более общем случае вместо 2-х сомножителей в агрегатном индексе может быть n сомножителей. Тогда факторный анализ проводится аналогично рассмотренному, но вместо суммирования двух разностей таких сумм будет n.
^

8.5. Общий индекс средних величин

Часто индексации подвергаются средние показатели в каждом периоде, тогда вводится общий индекс средних величин.

В качестве примера рассмотрим расчет индекса себестоимости продукции. Пусть z_0,1 – себестоимость единицы продукции в базовом и отчетном периодах (грн.), q_0,1 – объем произведенной продукции. Тогда средняя себестоимость в соответствующие периоды определяется как


И
х отношение

н
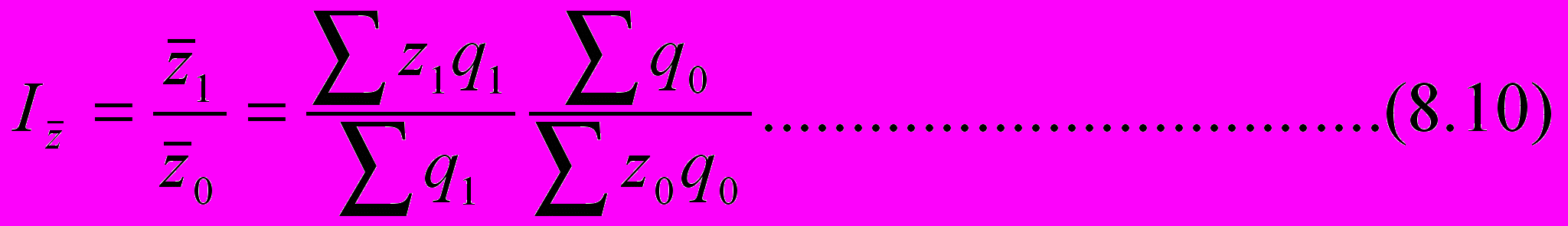
азывают общим индексом средних величин или индексом переменного состава. Последний термин связан с тем, что взвешивающие показатели q_i в каждом периоде меняются. Суммирование в (8.10) может производиться по разным видам продукции или по разным предприятиям.

Е
сли необходимо произвести анализ динамики себестоимости как таковой при неизменных весах q₁, используется индекс фиксированного состава

к
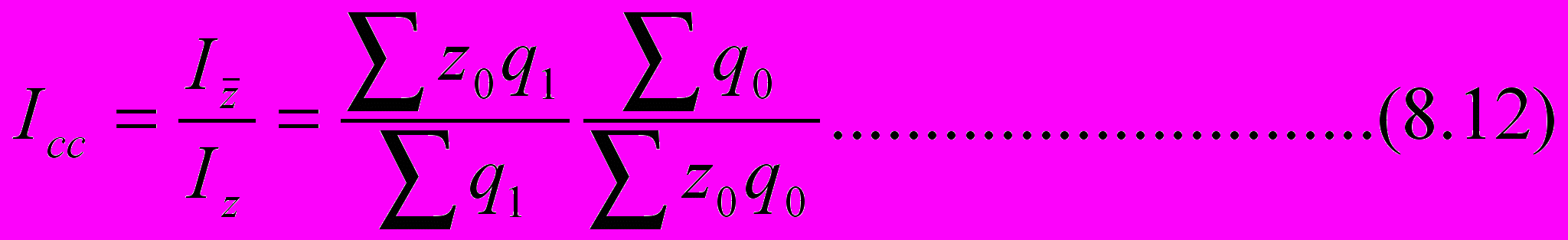
оторый является не чем иным, как агрегатным индексом себестоимости (аналогичным индексу цен (8.6)). Поскольку индекс (8.10) зависит от изменения весовой структуры продукции, а индекс (8.11) – не зависит, то отношение этих индексов

может характеризовать степень влияния структурных изменений на себестоимость продукции. Коэффициент (8.12) называется индексом структурных сдвигов.


Пример 8.4. Данные по объему производства и себестоимости продукции, производимой по двум технологиям А и В, приведены в таблице

Технология	Объем производства, шт.		^ Себестоимость, грн./шт.
	I полугодие	II полугодие	I полугодие	II полугодие
А	300	500	4,2	4,0
В	200	200	3,0	2,6

Определить индексы себестоимости переменного, фиксированного состава и индекс структурных сдвигов.

С
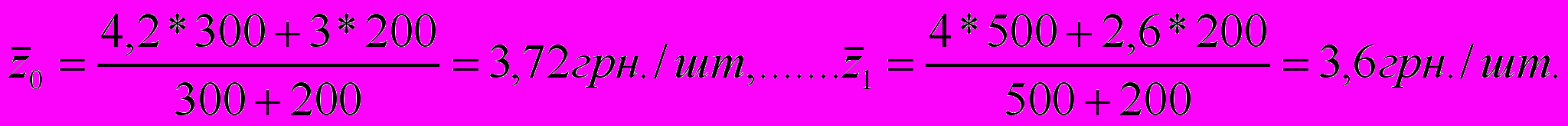
редние значения себестоимости для обеих технологий за два полугодия равны


О
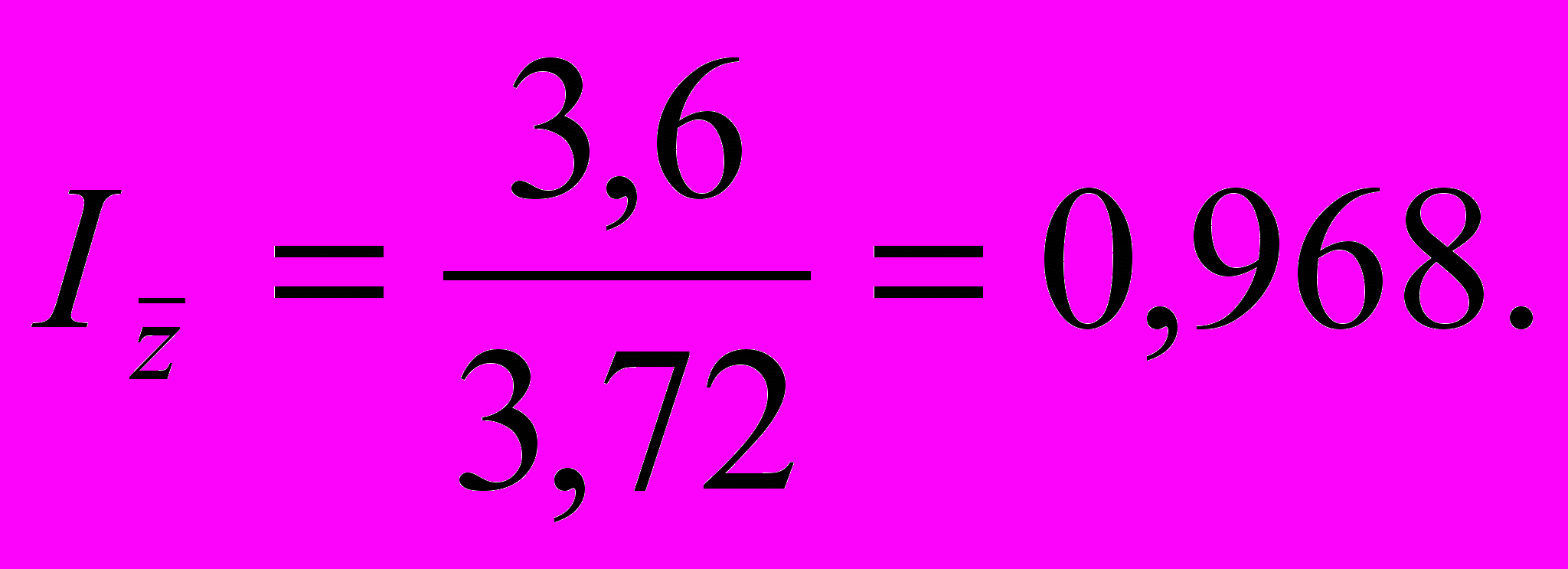
тсюда индекс переменного состава (8.10)

А
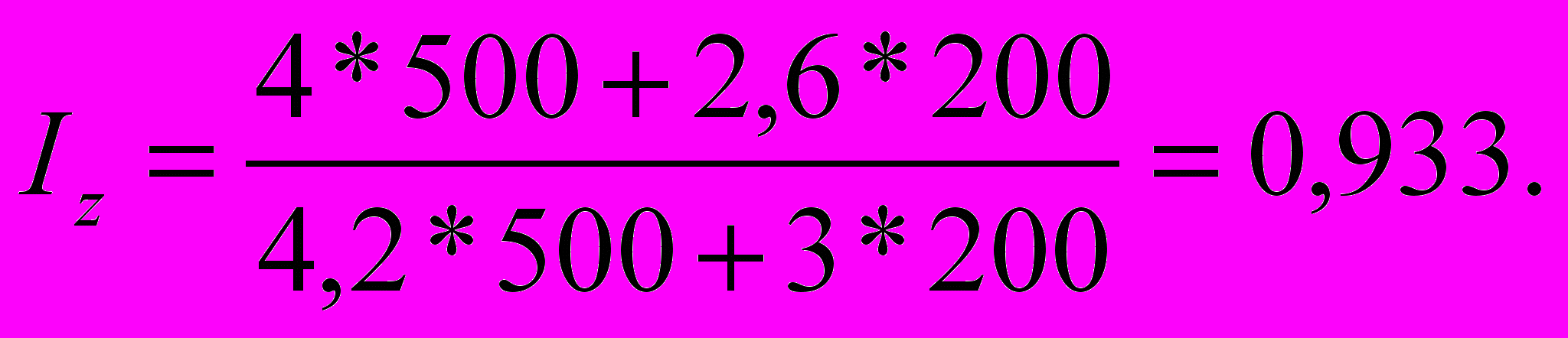
грегатный индекс себестоимости (фиксированного состава) согласно (8.11)


Т
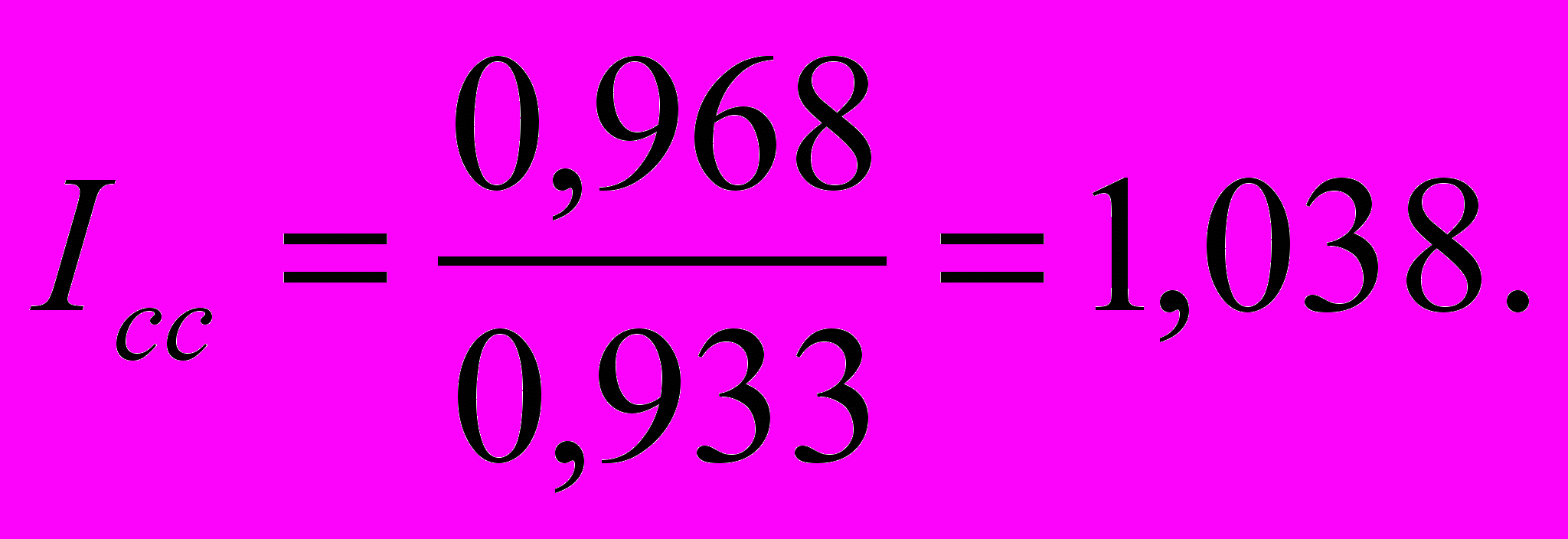
аким образом, индекс структурных сдвигов

Итак, динамика средней себестоимости ( с индексом 0,968) существенно зависит от влияния перспективной технологии В (средний индекс по технологиям 0,933) и несколько ухудшается (растет приблизительно на 4%) за счет нерационального распределения производства по технологиям (удельный вес старой технологии А вдвое выше, чем новой В).


Задачи

1. Производство и себестоимость металлопродукции характеризуется данными

Металл	Себестоимость, т. грн./тонна		Произведено, т. тонн
	1997 г	1998 г	1997 г	1998 г
Сталь	100	96	4	5
Чугун	52	50	12	10
Легир.сталь	145	140	3	5

Рассчитать:

• агрегатные индексы производства и себестоимости продукции;
  
• сводный индекс затрат производства;
  
• экономию средств за счет снижения себестоимости и за счет роста производства.
  

2. Импорт горючего в регион в 1996-1998 гг составил (в млн. грн.)

Годы	1996 г	1997 г	1998 г
В текущих ценах	310	360	490
В ценах 1996 г	310	305	330

Определить за 1997 и 1998 гг индексы цен и объема продаж.

3. Объемы продаж и индексы биржевых цен акций трех эмитентов приведены в таблице

Эмитент	Объемы продаж, млн. грн.		Индекс цен
	Январь	Март
А	450	500	1,3
В	250	150	0,9
С	300	400	1,2

Определить общий индекс биржевых цен и абсолютный прирост объема продаж.

4. Имеются данные по затратам на производство и индексам объема производства завода бытовой техники

Продукция	Затраты на производство, млн.гр.		^ Индекс объема производства
	Июль	Август
Холодильники	34	29	0,95
Стиральн. маш.	18	15	0,8

Определить:

• общий индекс объема производства;
  
• общий индекс себестоимости продукции;
  
• абсолютный прирост затрат на производство за счет динамики себестоимости.
  

5. Данные об объеме производства и трудоемкости продукции, произведенной по разным технологиям, приведены в таблице

Технология	Объем производства, шт.		^ Затраты труда на 1 изд,час
	Баз.период	Отч. период	Баз. период	Отч. период
А	500	800	2	1,8
В	500	200	3	3

Определить:

• среднюю трудоемкость в базисном и отчетном периодах;
  
• индекс средней трудоемкости (переменного состава);
  
• агрегатный индекс трудоемкости (фиксированного состава);
  
• индекс структурных сдвигов.
  

Сделать выводы о влиянии технологии и структуры производства на трудоемкость продукции.