Лекция Случайные процессы и временные ряды. Типы стационарности случайных процессов. Оператор запаздывания. Теорема Вольда

Вид материала

Лекция

Подобный материал:

• Московский институт радиотехники, электроники и автоматики, 121.14kb.
• Методические указания [2], 102.07kb.
• Тема Введение в эконометрику, 220.73kb.
• Случайные процессы и динамические системы, 34.5kb.
• Кыргызско-турецкий университет «манас» силлабус, 108.52kb.
• 9 Воспроизводственные циклы и временные лага Типы воспроизводственных циклов и их продолжительность, 62.98kb.
• Утверждаю, 166.99kb.
• Примерная рабочая программа по дисциплине: «теория вероятностей, математическая статистика, 83.07kb.
• Тем Введение в моделирование, 34.05kb.
• Задачи по теории вероятностей и математической статистике, 57.05kb.

Планы лекций

Лекция 1. Случайные процессы и временные ряды. Типы стационарности случайных процессов. Оператор запаздывания. Теорема Вольда

1. Введение: зачем все это нужно?

2. Случайные процессы и временные ряды

• определение временного ряда
  
• определение дискретного случайного процесса
  

3. Сильная и слабая стационарность случайных процессов

• определение строго стационарного процесса
  
• 3 следствия строгой стационарности
  
• определение автоковариационной функции случайного процесса
  
• определение слабо стационарного случайного процесса
  
• причинно-следственные связи между строго и слабо стационарными случайными процессами
  
• примеры (белый шум)
  

4. Оператор запаздывания и его свойства

5. Теорема Вольда и ее применение

Лекция 2. Обратимость и слабая стационарность случайных процессов. Однородные разностные уравнения.

1. Обратимость дискретных случайных процессов

• определение обратимого дискретного случайного процесса
  
• МА(1) в общем виде  условия на
  
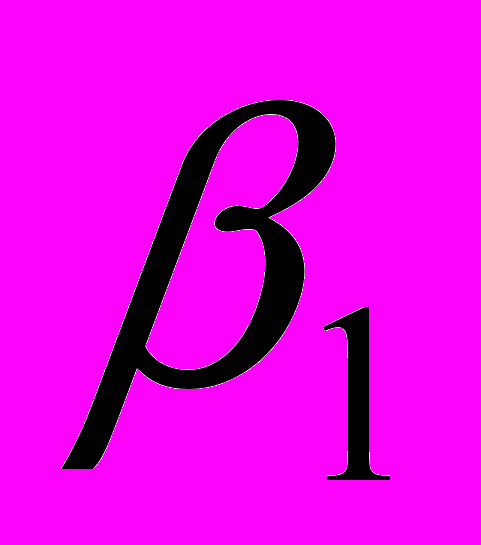
• МА(2) в общем виде  условия на корни
  
• МА(q) в общем виде  условия на корни
  
• характеристическое/обратное характеристическое уравнение  условия на корни
  

2. Слабая стационарность дискретных случайных процессов

• определение слабо стационарного дискретного случайного процесса
  
• AR(1) в общем виде  условия на
  
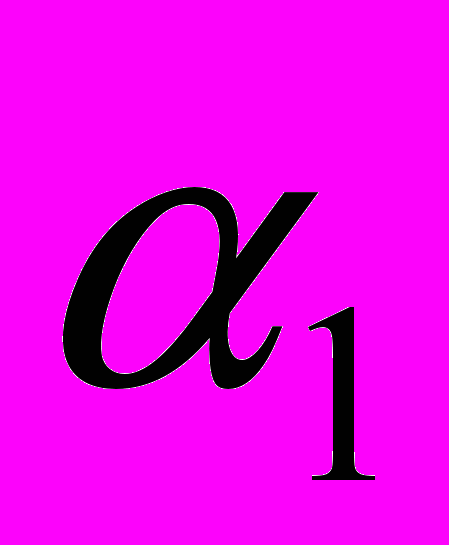
• AR(2) в общем виде  условия на корни
  
• AR(p) в общем виде  условия на корни
  
• характеристическое/обратное характеристическое уравнение  условия на корни
  
• разностные уравнения  условия устойчивости и их эквивалентность условиям слабой стационарности
  

3. APMA(p, q): обратимость и слабая стационарность

• схема: условия на корни характеристических и обратных характеристических уравнений
  

4. Связь однородных разностных уравнений процесса и соответствующей автоковариационной функции

• вывод автоковариационной функции (метод Юла-Уокера)
  

Лекция 3. Автокорреляционная функция и метод Юла-Уокера

1. Автокорреляционная функция

• определение автокорреляционной функции
  
• примеры: скользящее среднее – МА(1), МА(2), МА(q)
  

2. Метод Юла-Уокера

• понятие о методе и системе уравнений Юла-Уокера
  
• примеры: авторегрессия – AR(1), AR(2), AR(p)
  
• примеры: ARMA(p, q)
  

3. Основной вывод

• идентификация процессов скользящего среднего по ACF
  
• невозможность идентификации процессов авторегрессии по ACF
  

Лекция 4. Частная автокорреляционная функция

1. Частная автокорреляционная функция (PACF)

• определение частной автокорреляционной функции
  

2. Метод Юла-Уокера при выводе частной автокорреляционной функции

• понятие о методе и системе уравнений Юла-Уокера
  
• примеры: авторегрессия – AR(1), AR(2), AR(p)
  
• примеры: скользящее среднее – МА(1), МА(2), МА(q)
  
• примеры: ARMA(p, q)
  

3. Основной вывод

• идентификация процессов авторегрессии по PACF
  
• невозможность идентификации процессов скользящего среднего по PACF
  

4. Общая таблица для ACF и PACF различных случайных процессов

5. Свойства ACF и PACF слабо стационарных случайных процессов

• сходимость к нулю ACF и PACF слабо стационарных случайных процессов
  

Лекция 5. Метод Бокса-Дженкинса (этап 1)

1. Случайные процессы ARIMA(p, d, q)

• определение процесса ARIMA(p, d, q)
  
• примеры: RW, RWD, TS
  

2. Эргодичные случайные процессы

• определение эргодичного случайного процесса
  

3. Метод Бокса-Дженкинса (4 этапа)

• Этап 1. Идентификация параметров модели ARIMA(p, d, q)
  
• Этап 2. Оценивание параметров модели ARIMA(p, d, q)
  
• Этап 3. Тестирование модели ARIMA(p, d, q)
  
• Этап 4. Прогнозирование в модели ARIMA(p, d, q)
  

4. Этап 1. Идентификация параметров модели ARIMA(p, d, q)

• выборочные автокорреляционная и частная автокорреляционная функции
  

• определение выборочной автокорреляционной функции
  
• определение выборочной частной автокорреляционной функции
  
• свойства выборочных моментов случайного процесса
  

• идентификация параметров модели ARIMA(p, d, q)
  

Лекция 6. Метод Бокса-Дженкинса (этапы 2-3)

1. Этап 2. Оценивание параметров модели ARIMA(p, d, q)

• оценивание модели AR(p)
  

• свойства оценок модели AR(p)
  

• оценивание модели МА(q)
  

• метод максимального правдоподобия
  
• метод поиска на сетке
  
• свойства оценок модели МА(q)
  

• оценивание модели ARMA(p, q)
  

2. Этап 3. Тестирование модели ARIMA(p, d, q)

• информационные критерии (AIC, BIC)
  
• тесты на отсутствие автокоррелированности (в остатках модели) – Q*(s), Q(s), BG-LM
  
• тест на нормальность (JB)
  
• тест на отсутствие условной гетероскедастичности в остатках (ARCH)
  

Лекция 7. Метод Бокса-Дженкинса (этап 4)

1. Схема оценки модели ARIMA(p, d, q) (этапы 1-3)

• идентификация параметров модели d, p, q
  
• оценивание модели ARMA(p*, q*) для ряда
  
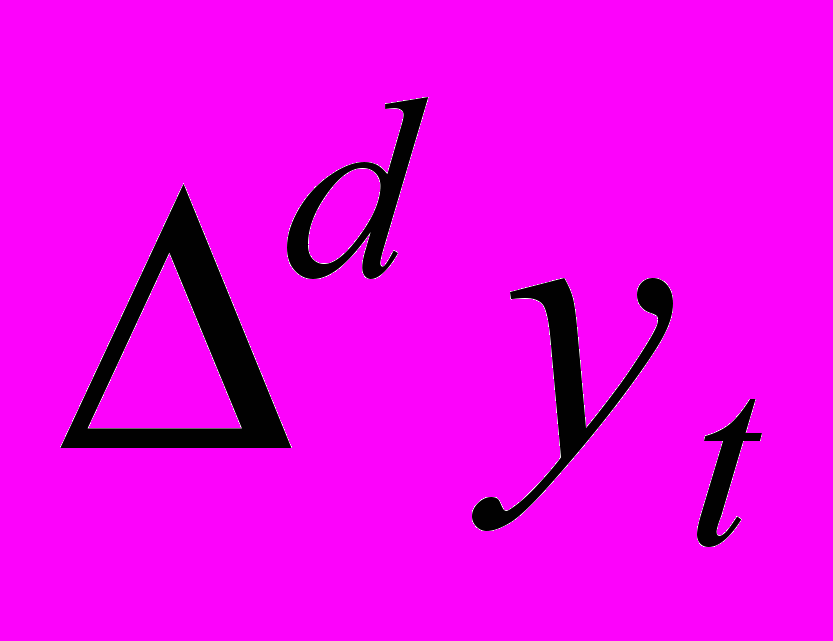
• тестирование модели и сужение класса получаемых моделей
  

2. Этап 4. Прогнозирование в модели ARIMA(p, d, q)

• прогноз как условное математическое ожидание
  
• ошибка прогнозирования и дисперсия ошибки прогнозирования
  
• статистики качества прогнозов (RMSE, МАЕ, МАРЕ)
  
• примеры: AR(1), MA(1), ARMA(1, 1)
  

Лекция 8+Семинар 8: Контрольная работа

Лекция 9. Случайные процессы с детерминированным и стохастическим трендом

1. Понятие нестационарного процесса

• нарушение условий слабой стационарности случайного процесса
  
• примеры не стационарных временных рядов (TS, DS)
  
• результаты Нельсона и Плоссера (Nelson, Plosser, 1982)
  
• понятие «кажущейся регрессии»
  

2. Случайные процессы, стационарные около тренда

• определение
  
• свойства первых и вторых моментов
  
• передифференцирование и его последствия
  

3. Случайные процессы, стационарные в разностях

• определение
  
• свойства первых и вторых моментов
  
• недодифференцирование и его последствия
  

4. Сравнение свойств стационарных и нестационарных случайных процессов (таблица)

Лекция 10-12. Тесты на единичные корни. Процедура Доладо-Дженкинсона-Сосвилла-Риверо

1. Тест Дикки-Фуллера на единичные корни

• свойства оценок МНК модели при наличии единичных корней в данных
  
• три спецификации теста Дикки-Фуллера: оцениваемые модели, нулевые и альтернативные гипотезы
  
• ADF-тест
  

2. Особенности (недостатки) теста Дикки-Фуллера

• условия на остатки модели
  
• низкая мощность
  
• предположения о детерминированном тренде
  
• зависимость результатов от выбора числа запаздывающих разностей
  

3. Методы борьбы с недостатками теста Дикки-Фуллера

• понятие о тесте Филлипаса-Перрона и др.
  
• использование тестов, обладающих более высокой мощностью (примеры)
  
• понятие о тестах Перрона и Зивота-Эндрюса
  
• методы выбора числа запаздывающих разностей
  

4. Процедура Доладо-Дженкинсона-Сосвилла-Риверо

5. Другие тесты на единичные корни (тест Филлипса-Перрона, тест Перрона, тест Зивота-Эндрюса)

Лекция 13. Коинтеграция. Процедура Энгла-Гренджера. Тест на причинность по Гренджеру

1. Определение интегрированного случайного процесса

2. Коинтегрированные случайные процессы

• определение коинтегрированных случайных процессов, коинтеграционного соотношения и коинтегрирующего вектора
  
• примеры
  

3. Процедура Энгла-Гренджера

• 1 этап – тест на отсутствие коинтеграция
  
• 2 этап – построение модели коррекции ошибками (ЕСМ)
  

4. Тест на причинность по Гренджеру

Лекция 14. Векторная авторегрессия. Функция импульсного отклика

1. Векторная авторегрессия

• Определение, различные формы записи
  
• слабая стационарность процесса векторной авторегрессии: определение, условия слабой стационарной
  
• математическое ожидание векторной авторегрессии (для слабо стационарного случая)
  
• оценивание векторной авторегрессии
  

2. Функция импульсного отклика

• определение
  
• свойства
  
• примеры
  

Лекция 15. Векторная модель коррекции ошибками. Тест Йохансена

1. Векторная модель коррекции ошибками

• связь между VAR и VECM
  
• условия наличия коинтеграции
  

Тест Йохансена (схема)

• схема теста
  
• trace statistic
  
• max statistic
  
• 5 случаев для теста Йохансена