Случайные процессы и динамические системы
| Вид материала | Документы |
- Программа курса лекций, 51.42kb.
- О некоторых особенностях интегрирования обыкновенных дифференциальных уравнений, описывающих, 18.79kb.
- Примерная рабочая программа по дисциплине: «теория вероятностей, математическая статистика, 83.07kb.
- 14. Лекция: Позиционно-силовое управление в системе робота-станка, 113.23kb.
- Московский институт радиотехники, электроники и автоматики, 121.14kb.
- Программа дисциплины «Динамические системы» Направление, 73.11kb.
- Рабочая программа дисциплины «Дискретные динамические системы», 110.59kb.
- Лекция Случайные процессы и временные ряды. Типы стационарности случайных процессов., 91.21kb.
- Программа государственного экзамена по направлению (магистерская подготовка) 230100., 37.35kb.
- Линейная регрессия и метод наименьших квадратов, 177.63kb.
СЛУЧАЙНЫЕ ПРОЦЕССЫ И ДИНАМИЧЕСКИЕ СИСТЕМЫ
(в рамках с/к “Теория вероятностей и математическая статистика”)
проф. В.И. Оселедец
1/2 года, 5 курс
1. Обобщенные случайные процессы. Белый гауссовский шум как производная от винеровского процесса. Ковариационная функция белого шума. Характеристический функционал белого шума. [1, гл. 3, § 1-4], [2, § 3.1, 3.3, 3.4].
2. Производящий функционал процесса. Моменты и семиинварианты процесса. Связь моментов и семиинвариантов процесса. [3, гл. 2, § 1].
3. Гауссовские процессы. Производящий функционал. Моменты [3, гл. 2, § 1].
4. Критерий эргодичности для гауссовского процесса [9, лекция 13].
5. Критерий перемешивания для гауссовского процесса [9, лекция 13].
6. Преобразования, сохраняющие меру и стационарные (в узком смысле) процессы [5, гл. 5, § 1], [6, гл. XVI, § 1, 2], [10, лекция 1], [9, лекция 2], [7, § 2.12-13].
7. Оператор (изометрический, унитарный) динамической системы в
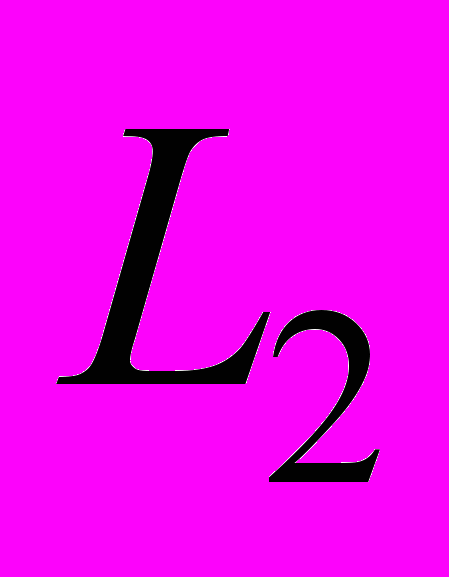. Инвариантные векторы и эргодичность [6, гл. XVI, § 3], [5, гл. 5, §2].8. Инвариантная
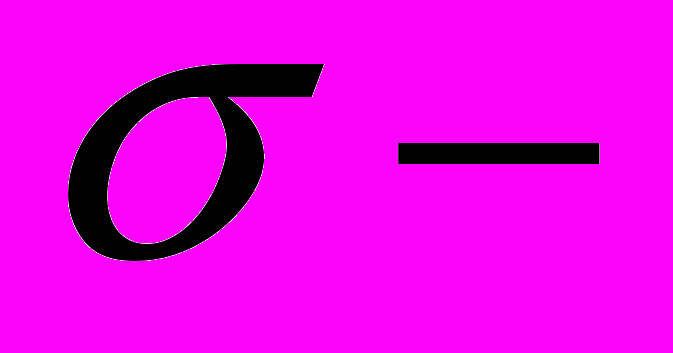алгебра и эргодичность.9. Спектральное представление стационарного процесса как следствие спектральной теоремы для унитарного оператора [6, гл. XVI, § 5].
10. Перемешивание, убывание ковариационных функций. Слабое перемешивание, непрерывность спектральных мер и критерий Винера. [10, лекция 2].
11. Нормальное упорядочение и экспонента Вика для гауссовской величины. Полиномы Эрмита как виковские степени. Их ортогональность. Дисперсия виковской степени. Базисность виковских степеней [3, гл. 2, § 2].
12. Виковская экспонента для двумерного гауссовского вектора. Виковские степени. Задача о максимальном коэффициенте корреляции. [3, гл. 2, § 2], [лекции].
13. Виковская экспонента и виковские степени для гауссовского процесса. Разложение Фока в ортогональную прямую сумму
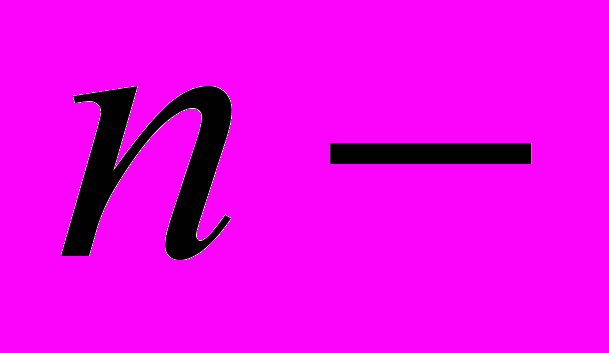частичных подпространств [лекции].14. Спектральное представление
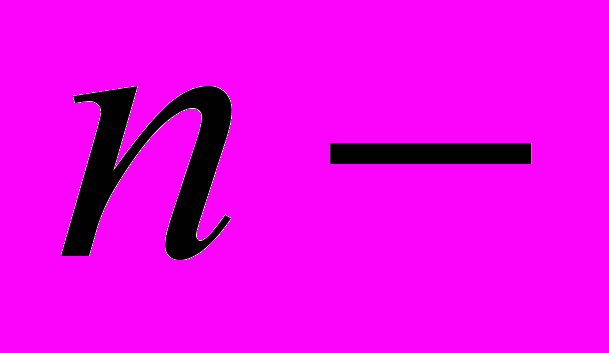частичного подпространства для гауссовского стационарного процесса. Спектральное представление унитарного оператора динамической системы в 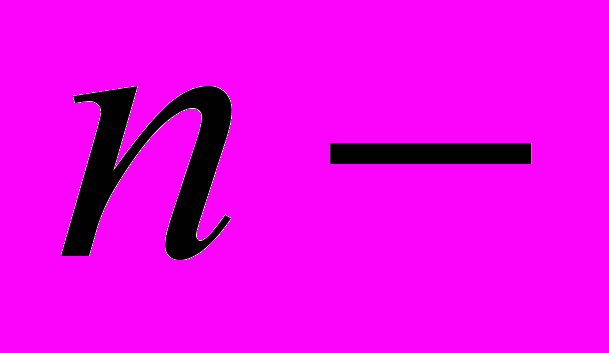частичном подпространстве [лекции].15. Спектр виковской степени
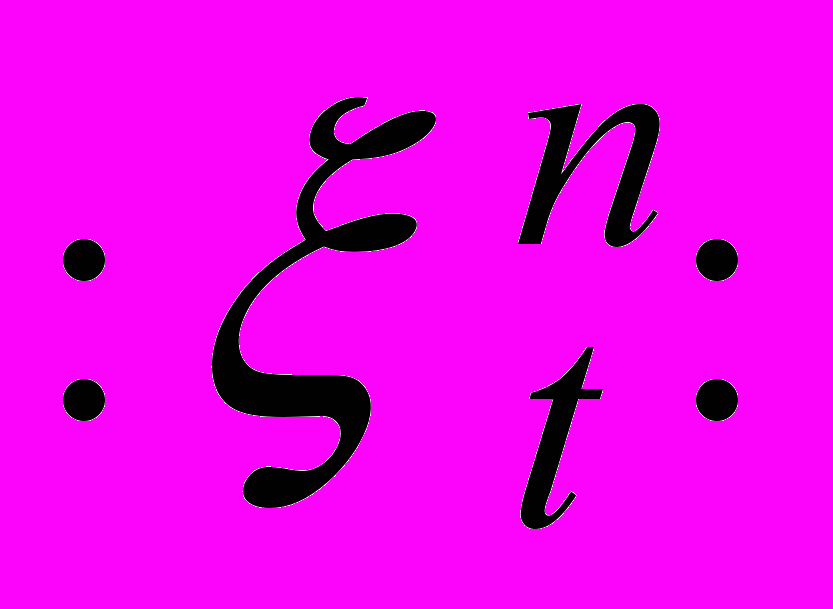для гауссовского стационарного процесса [лекции].16. Максимальный спектральный тип динамической системы [лекции].
17. Максимальный спектральный тип гауссовской динамической системы [лекции].
18. Нормальное упорядочение и кратные стохастические интегралы, представление нелинейных функционалов от гауссовского процесса. [лекции]
19. Операторы рождения-уничтожения. Канонические коммутационные соотношения и гауссовские процессы и поля. Нормальное упорядочение. Свободные квантовые поля. Некоммутативные гауссовские процессы и квази-свободные состояния [лекции].
20. Операторы рождения-уничтожения. Канонические антикоммутационные соотношения. Нормальное упорядочение. Фермиевские квазисвободные состояния [лекции].
21.
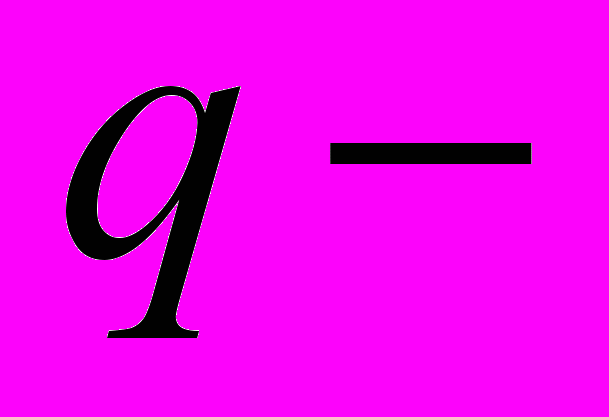коммутационные соотношения, 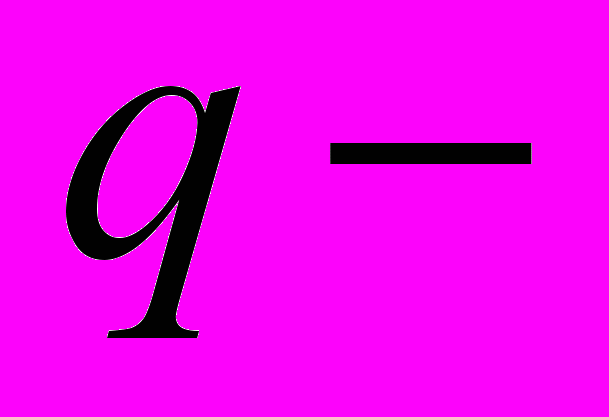многочлены Эрмита. 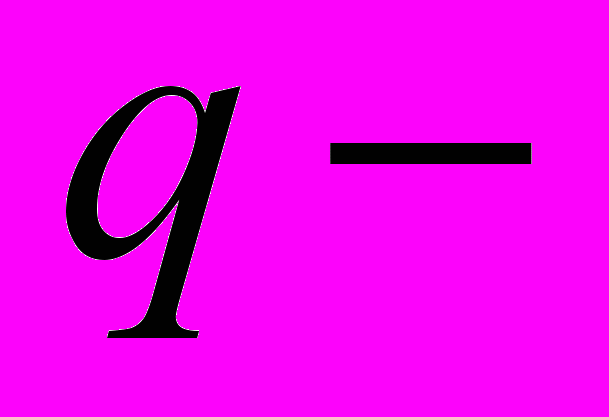гауссовские величины. Нормальное упорядочение.22. Свободные (
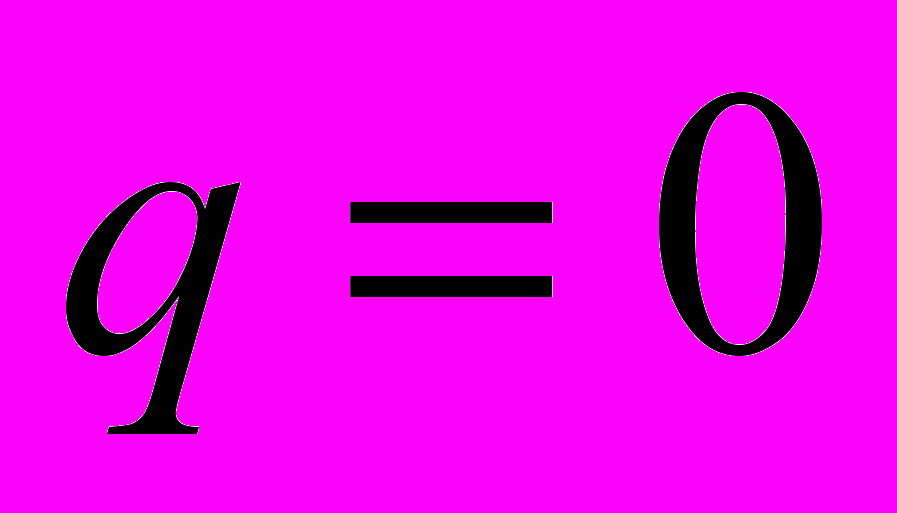) случайные процессы. Свободные гауссовские величины. Правило вычисления моментов, числа Каталана. Случайные матрицы большого порядка, сходимость к свободному гауссовскому распределению (полукруговой закон Вигнера) [8].23. Свободная свертка мер, свободные моменты и семиинварианты, преобразование Коши-Стилтьеса [8].
24. Свободные сверточные полугруппы, уравнение Бюргерса и дайсоновское броуновское движение. Свободное броуновское движение [8].
25. Алгебра фон Неймана. Фактор. Типы факторов. Конструкция фон Неймана алгебры фон Неймана по динамической системе [12].
26. Спиновые системы, гиперфинитные факторы и конструкция фон Неймана. Факторы Пауерса [12].
27. Модулярный оператор и меры Гиббса для спиновых систем.
28. Подфакторы. Индекс Джонса подфактора. Подфакторы Джонса и модели статистической механики [11].
Литература
1. Гельфанд И.М., Виленкин Н.Я. Некоторые применения гармонического анализа. Оснащенные гильбертовы пространства (Обобщенные функции, выпуск 4). М., Физматгиз, 1961.
2. Хида Т. Броуновское движение. М., Мир, 1988.
3. Малышев В.А., Минлос Р.А. Гиббсовские случайные поля. М., Наука, 1985.
4. Корнфельд И.П., Синай Я.Г., Фомин С.В. Эргодическая теория. М., Наука, 1980.
5. Ширяев А.Н. Вероятность. М., Наука, 1989.
6. Ибрагимов И.А., Линник Ю.В. Независимые и стационарно связанные случайные величины. М., Наука, 1965.
7. Биллингслей П. Эргодическая теория и информация. М., Мир, 1969.
8. Voiculescu D.V., Dykema K., Nica A. Free random variables. CRM Monograth Series, № 1, Amer. Math. Soc., Providence, 1992.
9. Синай Я.Г. Введение в эргодическую теорию. М., Фазис, 1966.
10. Синай Я.Г. Современные проблемы эргодической теории. М., Физматгиз, 1995.
11. Jones V.F. Index for subfactors. Invent. math., 72, 1-15, 1983.
12. Sunders V.S. Invitation to von Neumann algebras. Springer-Verlag, 1986.