Анализ финансового состояния предприятия

Вид материала

Реферат

Содержание 2.4. Расчет корреляции по конкретным показателям

Подобный материал:

• Использование экономико-математических методов для определения финансового состояния, 47.07kb.
• Методические основы проведения анализа финансового состояния предприятия правовое обеспечение, 29.74kb.
• Анализ финансового состояния предприятия по данным бухгалтерской отчетности Введение, 39.4kb.
• Методика анализа финансового состояния 14 2 анализ финансового состояния ООО «Аллегро», 1391.2kb.
• Методические основы стабилизации деятельности предприятия 26 Исследование причин кризисного, 61.35kb.
• Анализ финансового состояния предприятия 10 Сущность, значение и задачи анализа финансового, 289.44kb.
• Методика анализа финансового состояния предприятия. Экспресс-анализ. Анализ экономической, 26.41kb.
• Анализ и планирование денежных потоков предприятия Анализ финансового состояния и бюджетирование, 91.78kb.
• Темы курсовых работ по дисциплине «Финансовый анализ в менеджменте». Анализ финансовой, 26.59kb.
• Анализ финансовой устойчивости предприятия, 141.45kb.

2.4. Расчет корреляции по конкретным показателям

Если связь между показателем не является строго детерминированной, то она корреляционная. Она характеризуется тем, что, помимо изучаемых условных факторов, на результативный показатель оказывают влияние и побочные факторы, искажающие влияние основного.

Обязательным условием применения корреляционного метода является массовость значений изучаемых показателей, позволяющая выявить тенденцию, закономерность развития.

Корреляция может быть парной и множественной.

Парная корреляция – это связь между двумя показателями, один из которых является фактором, другой – результативным показателем.

Множественная корреляция – связь между несколькими факторами и одним результативным показателем.

Алгоритм расчёта при корреляционном анализе связи парной корреляции состоит из ряда этапов.[7, c.35]

Этап 1. Производится отбор наиболее важных существенных факторов, влияющих на результативный показатель. При отборе факторов учитываются причинно-следственные связи между показателями, причём все факторы должны быть количественно измеримы.

Этап 2. Данные из таблицы наносятся на плоскость координат – строится корреляционное поле.

Этап 3. Производится обоснование формы связи:

• по форме корреляционного поля;
  
• путём визуального анализа ранжирования ряда.
  

Этап 4. Выбор и решение уравнения регрессии осуществляется с применением ПЭВМ.

Метод множественной корреляции применяется в случаях, когда результирующий показатель зависит от нескольких взаимно независимых факторов. При этом применяется уравнение множественной регрессии:

Коэффициент корреляции находится по формуле:



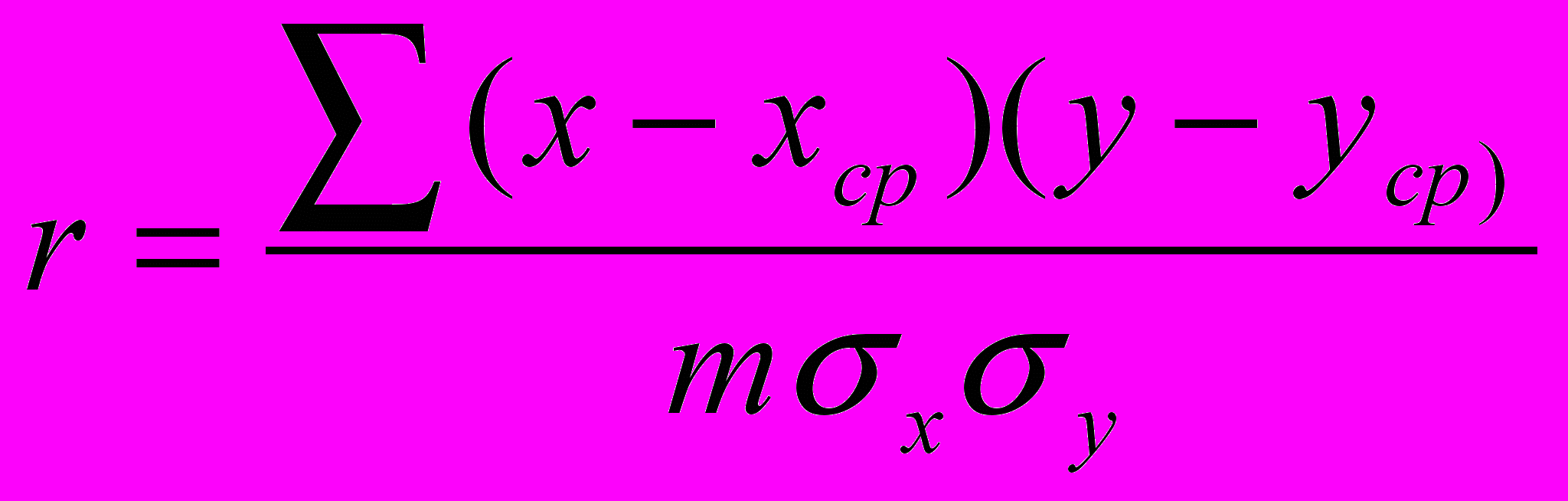
где: x_ср и y_ср – средние арифметические значения величин x и y:

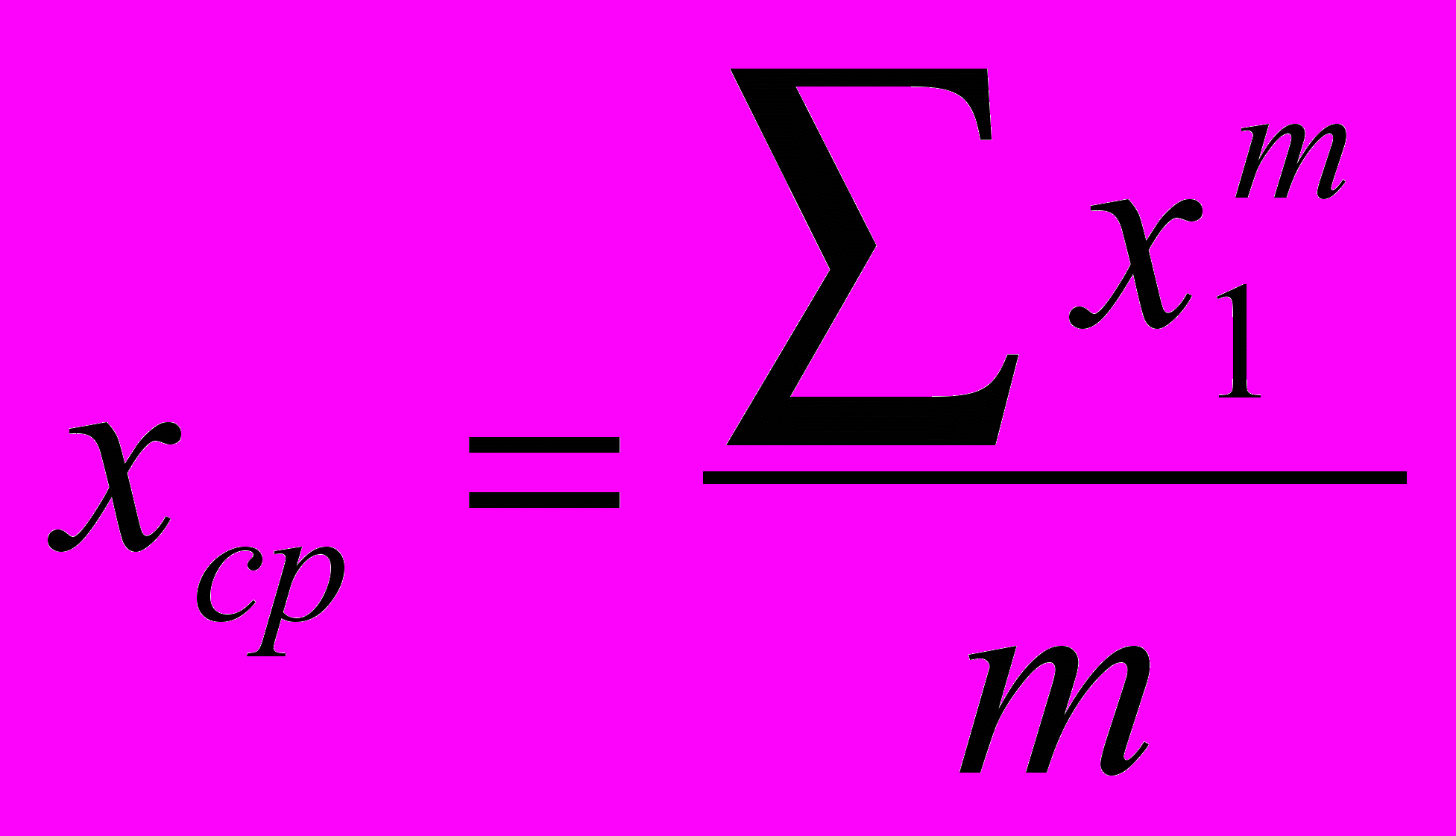
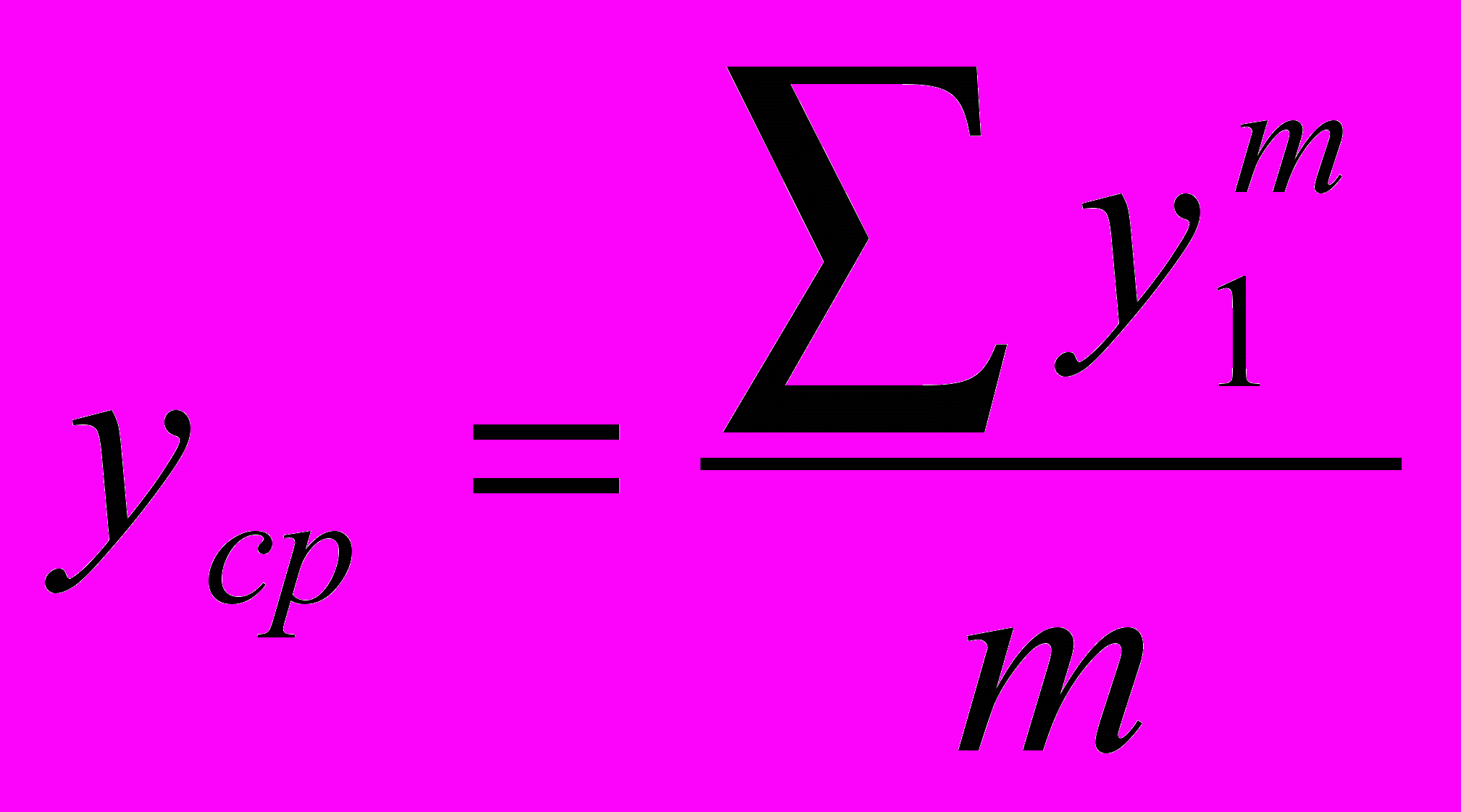(36)

m – количество показателей; σ_x σ_y – средние квадратические отклонения х и у от х_ср и у_ср. Они рассчитываются по формулам:

σ_x = √∑(х – х_ср)²/m; σ_y = √∑(у – У_ср)²/m; (37)

С помощью парного линейного коэффициента корреляции измеряется теснота связи между двумя признаками. Линейный коэффициент корреляции чаще всего рассчитывается по формуле:



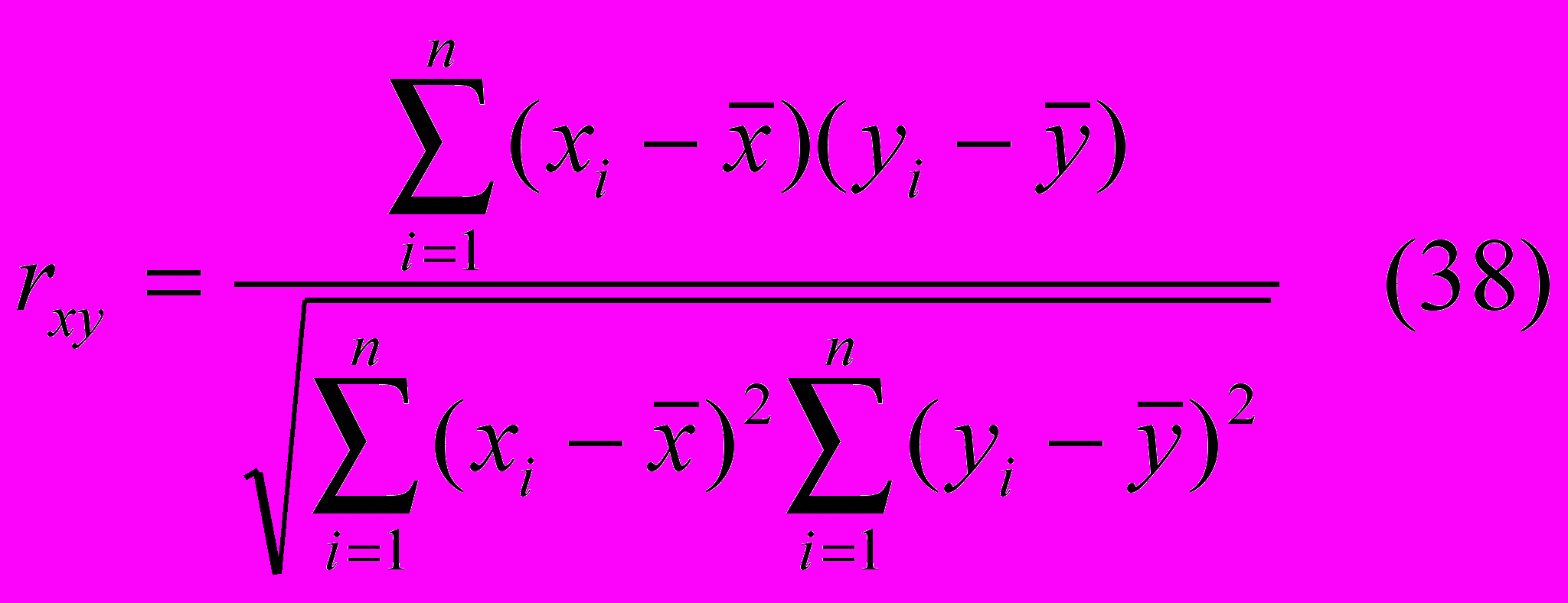
где x_i и y_i — значения признаков х и у соответственно для i-ro объекта, i=1,.., n; n — число объектов; 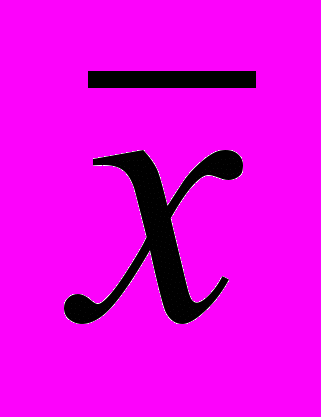и 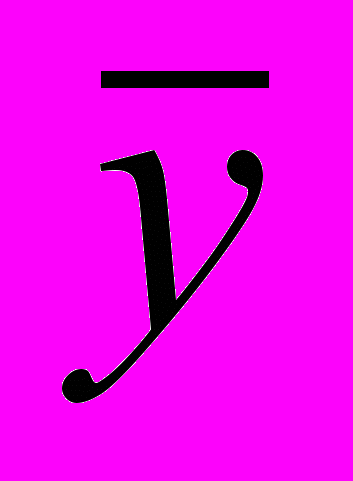— средние арифметические значения признаков х и у соответственно.

Линейный коэффициент корреляции изменяется в пределах от —1 до +1. Равенство коэффициента нулю свидетельствует об отсутствии линейной связи. Равенство коэффициента —1 или +1 показывает наличие функциональной связи. Знак «+» указывает на связь прямую (увеличение или уменьшение одного признака сопровождается аналогичным изменением другого признака), знак «—» — на связь обратную (увеличение или уменьшение одного признака сопровождается противоположным по направлению изменением другого признака).

Линейный коэффициент корреляции является показателем взаимной связи между признаками и не дает представления о том, какой из признаков является факторным, а какой — результативным (в формуле (3.1) признаки х и у совершенно равноправны).

С помощью парного линейного коэффициента корреляции выявляется связь между двумя признаками, один из которых можно рассматривать как результативный, другой — как факторный. Но в действительности на результат воздействуют несколько факторов. В связи с этим возникают два типа задач: задачи измерения комплексного влияния на результативную переменную нескольких переменных и задачи определения тесноты связи между двумя переменными при фиксированных значениях остальных переменных. Задачи первого типа решаются с помощью множественных коэффициентов корреляции, задачи второго типа — с помощью частных коэффициентов корреляции.

Частный, или чистый, коэффициент корреляции между двумя признаками при исключении влияния третьего признака (обозначим его символом r_12.3) рассчитывается по формуле:

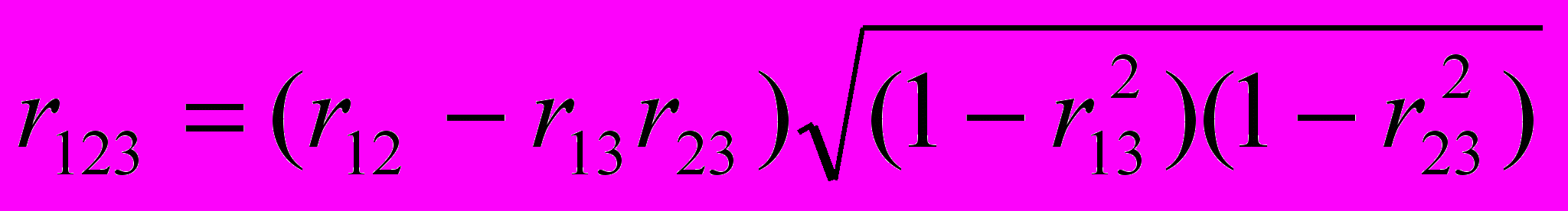, (39)

где индексы при r показывают номера признаков, связь между которыми оценивается.

Частный коэффициент корреляции первого и второго признаков при исключении влияния третьего оценивает тесноту линейной корреляционной связи между первым и вторым признаками при фиксированном значении третьего признака. Другими словами, он оценивает влияние на результативный (первый) признак изменения лишь второго признака.

Значения частных коэффициентов корреляции заключаются в тех же пределах от —1 до +1, что и значения парных коэффициентов корреляции, и так же интерпретируются.

Множественный, или совокупный, коэффициент корреляции для случая трех признаков, один из которых — результативный (с номером 1) и два —факторных (с порядковыми номерами 2 и 3) рассчитывается по формуле:

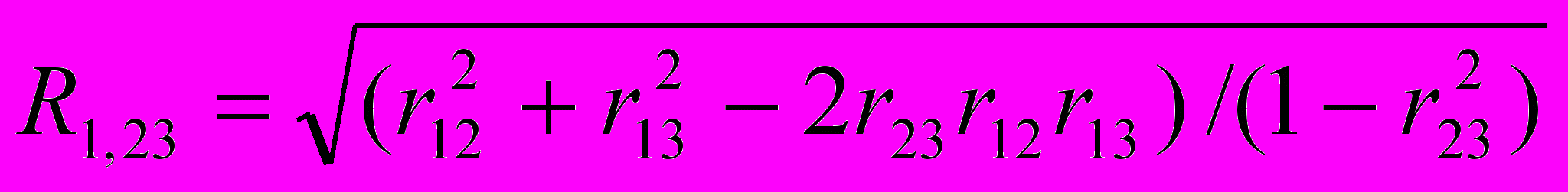(40)

Множественный коэффициент корреляции является показателем тесноты линейной связи между результативным признаком и совокупностью факторных признаков.

Множественный коэффициент корреляции изменяется в пределах от 0 до 1. Равенство его нулю говорит об отсутствии линейной связи, равенство единице — о функциональной связи. Указаний на то, является ли связь прямой или обратной, коэффициент не дает.

Линейный коэффициент корреляции оценивает тесноту взаимосвязи между признаками и показывает, является ли связь прямой или обратной. Но понятие тесноты взаимосвязи часто может быть недостаточным при содержательном анализе взаимосвязей. В частности, коэффициент корреляции не показывает степень воздействия факторного признака на результативный. Таким показателем является коэффициент детерминации (обозначим его D), для случая линейной связи представляющий собой квадрат парного линейного коэффициента корреляции (D=r²) или квадрат множественного коэффициента корреляции. Его значение определяет долю (в процентах) изменений, обусловленных влиянием факторного признака, в общей изменчивости результативного признака.