Федеральная программа книгоиздания России Рецензенты: канд психол наук С. А. Исайчев, доктор биол наук И. И. Полетаева Равич-Щербо И. В. и др. Р12
| Вид материала | Программа |
- Вестник балтийской педагогической академии вып. 94. – 2010 г. Актуальные проблемы нравственного, 2431.92kb.
- Рецензенты: профессор, доктор психол наук Филонов Л. Б., вед науч сотрудник, канд психол, 2609.63kb.
- Научный выпуск вестник балтийской педагогической академии вып. 29. – 2000 г. Поиск, 1745.18kb.
- Общеобразовательная программа дошкольного образования Авторский коллектив, 5619.19kb.
- Образовательная программа дошкольного образования Москва «Просвещение», 5670.3kb.
- Введенским Игорем Витальевичем Рецензенты доктор психол наук В. А. Лабунская канд психол, 375.9kb.
- Отчет о проведении Международной научной конференции-семинара «Современные методы психологии», 97.76kb.
- Приглашение и программа разнообразие почв и биоты северной и центральной азии, 521.14kb.
- Пояснительная записка, 12621.4kb.
- В организации совместных отношений, 1137.14kb.
13- 1432
193
2. МЕТОДЫ АНАЛИЗА ПСИХОГЕНЕТИЧЕСКИХ ЭМПИРИЧЕСКИХ ДАННЫХ
Как говорилось в гл. VII, психогенетиками была разработана система методов, которые позволяют оценить составляющие фенотипи-ческой дисперсии; все они построены на решении систем уравнений, описывающих сходство родственников различных степеней родства. К их анализу мы теперь и переходим.
КЛАССИЧЕСКИЙ АНАЛИЗ РОДСТВЕННЫХ КОРРЕЛЯЦИЙ
Сходство родственников, принадлежащих к разным поколениям (предки — потомки), обычно оценивается коэффициентом корреляции Пирсона, который называют также межклассовым коэффициентом корреляции. В случае близнецов и сиблингов применяется коэффициент внутриклассовой корреляции, подсчитываемый на основе дисперсионного анализа:
где х1' и х1j — значения одного и того же признака у близнецов одной пары.
Использование внутриклассовой корреляции в данном случае обусловлено тем, что нет генетического критерия для отнесения того или иного члена пары в тот или другой вариационный ряд. В табл. 8.4 приведен пример вычисления внутриклассовой корреляции для МЗ близнецов.
Таблица 8.4 Вычисление внутриклассового коэффициента корреляции
| Значение признака | х1 - х2 | (х1 - х2) | х1+ х2 | (х1 + х2) | ||
| Пары | близнец 1 х1 | близнец 2 | ||||
| 1 | 9 | 1 | 2 | 4 | 16 | 256 |
| 2 i 4 5 | 4 i 2 4 | 6 2 1 i | -2 1 1 1 | 4 1 1 1 | 10 5 J 7 | 100 25 9 49 |
| СУММЫ 11 41 439 | | | | | |
194
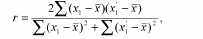
W = 11/2/5 = 1,1; 5 = {[439-41/5]/2/4-1,1}/2 = {[439-1681/5]/8-1,1}/2 =
= 5,875 R = 5,875 /(5,875 +1,1) = 0,842.
Внутриклассовый коэффициент корреляции, в отличие от межклассового, не изменяется при перемене мест членов пары.
При подсчете коэффициента корреляции обычно вычисляется и ошибка его измерения. Это важно, так как наличие ошибок измерения ведет к искажению коэффициента корреляции и, следовательно, при проведении генетического анализа по коэффициентам корреляции между родственниками будут получаться смещенные оценки компонентов дисперсии признака. В связи с этим производится поправка коэффициентов корреляции на дисперсию ошибки измерения, для чего проводят повторные измерения признаков у одних и тех же индивидов. Дисперсия ошибки измерения равна внутрипарной дисперсии (V0 = W), вычисленной по повторным измерениям. Когда дисперсия ошибки подсчитана, коррекция межклассовых коэффициентов корреляции осуществляется с использованием следующей формулы:
R = R [1+Ve1 /(S12 - Ve1 )][1+Ve2 /(S22 - Ve2)],
где Я — исходный коэффициент корреляции между первыми и вторыми родственниками по изучаемому признаку: Sb S2 — дисперсии признака у соответствующих родственников.
Использование индексов 1-й (например, родители) и 2-й (например, дети) групп родственников обусловлено тем, что указанные группы могут отличаться друг от друга по изучаемым признакам вследствие половых, возрастных и тому подобных различий.
Коррекция коэффициентов внутриклассовой корреляции (между близнецами, сиблингами) на дисперсию ошибки измерения проводится по формуле:
R = B/(B + W-Ve)
где В — межпарная дисперсия, W— внутрипарная дисперсия. Если приведенные в табл. 8.5 данные рассматривать как повторные измерения одних и тех же индивидов, то дисперсия ошибки измерения VС = W = 1,1, а внутриклассовая корреляция в данном случае соответствует коэффициенту воспроизводимости.
Корреляции разных типов родственников несут в себе специфическую информацию о разных составляющих фенотипической дисперсии в популяции (табл. 8.5). Например, при изучении пары приемный родитель — усыновленный ребенок можно получить оценку вклада
13*
195
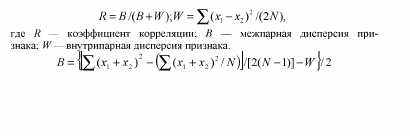
общей семейной и родительско-детской среды. При изучении же только корреляций биологических родителей и детей разделить составляющие генетической аддитивной дисперсии и родительско-детской среды невозможно, поскольку их объединяет и общая среда, и 50% общих генов. Этот метод применим только в сочетании по крайней мере с одним другим методом, который позволил бы разделить влияния генетических и средовых компонентов.
Таблица 8.5
Вклады аддитивного (Va), доминантного (Vd) и общего средового (VEC) компонентов фенотипической дисперсии в фенотипические корреляции разных типов родственников
| Типы родственников | VA | VD | Vec |
| Биологические родители и дети | 1/2 | 0 | Vc(bpo) |
| Приемные родители и дети | 0 | 0 | VС(АРО) |
| Сиблинги с одним общим родителем | 1/4 | 0 | Cc(hs) |
| Сиблинги | 1/2 | 1/4 | VС(FS) |
| Двуяйцевые близнецы | 1/2 | 1/4 | VC(DZ) |
| Однояйцевые близнецы | 1,0 | 1,0 | Vc(mz) |
Примечание. Здесь и далее:
ВРО — родители Х дети (biological parent-offspring); AP O — приемные родители Х дети (adopted parent-offspring); HS — полусиблинги (half-sibling); FS — полные сиблинги (full-sibling); DZ— ДЗ близнецы (dizygotic twins); MZ — МЗ близнецы (monozygotic twins).
С целью максимизации информации, полученной при анализе разных типов родственников, ученые совмещают несколько методов в рамках одного исследования. Выбор методов для исследования того или иного признака является специальной задачей. Главное правило здесь заключается в том, что количество независимых исходных статистик (т.е. количество корреляций между родственниками) должно превышать количество неизвестных в системе уравнений. Если это правило не выдерживается, система уравнений однозначного решения не имеет.
Например, представим себе, что мы исследуем по некоторому признаку биологические семьи, каждая из которых растит по крайней мере двух детей. Соответственно, мы можем определить корреляции по исследуемому признаку как между родителями и детьми, так и между сиблингами в данных семьях. Любая из этих пар будет иметь в среднем 50% общих генов, что позволяет, используя информацию из табл. 8.5, записать следующую систему уравнений:
ГВРО ~1 ' 2 * А ~"~ *С (ВРО) J ' " Р '
rFS ~Y ' 2 VA ' '4 V D +V C(FS) ] / V P .
196
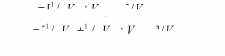
Чем больше различных пар родственников включено в анализ, тем больше компонентов дисперсии может быть определено однозначно и тем более сложные и разветвленные модели могут оцениваться.
В качестве иллюстрации рассмотрим два метода, используемых для разделения генетической и средовой составляющих фенотипической дисперсии в популяции (подробнее о методах психогенетики — в гл. VII).
Метод близнецов. Этот метод, без сомнения, был и до сих пор является одним из ведущих методов психогенетики. Классический вариант метода близнецов основывается на том, что монозиготные (МЗ) и дизиготные (ДЗ) близнецы характеризуются различной степенью генетического сходства, в то время как их среда может считаться приблизительно одинаковой. На языке составляющих фенотипической дисперсии (см. табл. 8.2 и 8.3) это можно выразить так:

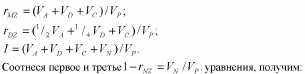
МЗ близнецы представляют собой идентичные генетические копии друг друга, поэтому теоретически корреляция МЗ близнецов по признаку, вариативность которого в популяции находится полностью под генетическим контролем, должна равняться 1,0. Разницу между 1,0 и реальной корреляцией МЗ близнецов можно объяснить влияниями индивидуальной среды или ошибки измерения (компонент Vn содержит в нерасчлененном виде обе эти составляющие).
Отметим, что приведенные закономерности соотношения МЗ и ДЗ близнецов справедливы только при следующих условиях (частично речь о них шла в гл. VII):
197
1. Центральным допущением при использовании метода близнецов в любом его варианте является допущение о равенстве среды МЗ и ДЗ близнецов. Важно отметить, что оно подразумевает не одинаковость близнецовых сред, а тот факт, что распределение (частота встречаемости и разброс) средовых компонентов монозиготных близнецов не превышает разнообразия сред дизиготных. Правомерность этого допущения до сих пор исследуется и обсуждается психогенетиками; если оно не справедливо, то получаемые этим методом оценки коэффициента наследуемости искажены. Как уже говорилось, это допущение касается не всей близнецовой среды, а только тех ее аспектов, которые связаны с изучаемым признаком (если они известны).
2. VgxЕ = 0, т.е. принимается допущение об отсутствии ГС-взаимодействия. Заметим, что в некоторых случаях такое допущение вполне правомерно, в большинстве же случаев оно требует тщательной эмпирической проверки.
3. Cov(g)(e) = 0, т.е. принимается допущение об отсутствии геyотип-средовой ковариации. Прямо проверить это допущение в рамках классического близнецового метода невозможно. Поэтому, как и в случае двух предыдущих допущений, отсутствие ГС-ковариации и корреляции при использовании классического метода близнецов принимается на веру.
4. Ассортативность по исследуемому признаку не отличается от нуля (т.е. ц. = 0). Как уже говорилось, это допущение для большинства исследуемых в психогенетике признаков неверно: неслучайность подбора супружеских пар у человека — скорее правило, чем исключение. Поэтому допущение об отсутствии ассортативности надо обязательно проверять (в том случае, если в литературе отсутствуют необходимые сведения) по данным о супружеских парах. В общем случае корреляция между супругами включает в себя компонент, обусловленный ассортативностью брака, и компонент, обусловленный влиянием семейных систематических средовых факторов. Самым простым и надежным способом проверки этого допущения является обследование родителей близнецов. Не имея данных о родителях (т.е. корреляций между родителями по исследуемому признаку), исследователь не может «развести» эффекты ассортативности и эффекты семейной среды. Наличие же значимой ассортативности повышает возможность получения ДЗ одинаковых генов от обоих родителей (у МЗ и без этого фактора их 100%), повышая rДЗ и тем самым снижая разность rМЗ - rДЗ и, следовательно, величину коэффициента наследуемости (о нем речь пойдет ниже).
5. В генетическом механизме изучаемого признака отсутствуют эпи-статические взаимодействия (Vt). Это условие принимается как должное практически во всех психологических исследованиях (многие исследователи принимают данное допущение a priori, даже не обсуждая его правомерность). Однако в ситуациях, когда это допущение не-
198
справедливо, оценки составляющих фенотипической дисперсии могут быть сильно искажены, поскольку эпистатическое взаимодействие генов может значительно уменьшить генетическое сходство ДЗ близнецов, тем самым увеличивая разницу между rМЗ и rДЗ и приводя к завышенным оценкам коэффициента наследуемости.
Однако даже в том (весьма неправдоподобном!) случае, когда исследуется психологический признак, для которого соблюдаются все вышеперечисленные условия, оценить все четыре компонента фенотипической дисперсии (VA,Vd ,Vc ,VN ) в рамках метода близнецов невозможно, так как четыре независимых величины не могут быть определены из трех линейных уравнений. Ученые, тем не менее, сделав несколько упрощающих допущений, разработали несколько способов оценки коэффициента наследуемости на основе метода близнецов. Отметим, что ни один из этих методов не является «правильным» или «неправильным» — каждый из них обладает определенными достоинствами и недостатками. Рассмотрим кратко хотя бы три наиболее часто встречающихся в литературе метода оценки коэффициента наследуемости.
КОЭФФИЦИЕНТ ХОЛЬЦИНГЕРА
К. Хольцингер предложил следующую формулу для оценки наследуемости:

КОЭФФИЦИЕНТ ИГНАТЬЕВА*
В качестве первой оценки величины генетической составляющей фенотипической дисперсии часто используется коэффициент Игнатьева, вычисляемый следующим образом:
* Данный способ оценки генетического компонента дисперсии и зарубежной психогенетике связан с именем Д. Фальконера, работа которого вышла в I960 г. Однако этот коэффициент был предложен еще в 1934 г. М.В. Игнатьевым. Кратко об этом см. во Введении, а также в работах В.М. Гиндилиса [97] и Б.И. Кочубея [132, гл. I]. В формуле Игнатьева используются иные символы, но, поскольку в современной науке утвердились приводимые далее обозначения, будем пользоваться ими и мы. В приводимой ниже формуле Еобщ — то же, что ЕС, a Eинд — то же, что EN в предыдущем тексте (см. табл. 8.3).
199
При наличии доминантного компонента дисперсии VD оценка наследуемости будет завышена.
Очевидно, что влияние любых факторов, изменяющих разницу между корреляциями двух типов близнецов (например, завышение корреляции между МЗ близнецами, возникающее в результате действия специфической для этого типа близнецов среды), будет влиять на эту оценку наследуемости. Хотя в последние годы появились и все чаще употребляются более современные и сложные методы статистического анализа, этот коэффициент, в силу своей аргументированности и простоты получения, остается в арсенале психогенетики. Более того, Р. Пломин предложил с помощью этой формулы оценивать — тоже в первом приближении, конечно, — и долю средовых компонентов:
где С — значение со-близнеца по исследуемому признаку (данный метод подразумевает выделение в каждой паре одного близнеца — условного пробанда, тогда второй близнец называется со-близнецом); Р — значение близнеца-пробанда по тому же признаку; R — коэффициент родства (1 для МЗ и 0,5 для ДЗ близнецов); PR — произведение
200
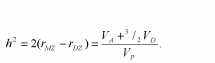
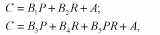
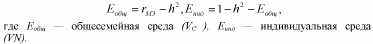
Правда, в оценку индивидуальной среды неизбежно включается часть дисперсии, вызванная ошибкой измерения. Возможность коррекции этого дефекта обсуждена выше.
МЕТОД ДЕ ФРИЗА И ФУЛКЕРА (ДФ-МЕТОД)
Дж. де Фриз и Д. Фулкер разработали две регрессионные модели: 1) классическую регрессионную модель, в которой частная регрессия значения со-близнеца на значение близнеца—условного пробанда и коэффициент родства представляет собой тест генетической этиологии исследуемого признака, и 2) расширенную регрессионную модель, предоставляющую прямое свидетельство того, насколько индивидуальные различия внутри исследуемой группы объясняются генетическими и средовыми влияниями. Эти два регрессионных уравнения записываются следующим образом:
значения пробанда по исследуемому признаку на коэффициент родства; А — константа регрессионного уравнения.
Решение этих уравнений позволяет оценить следующие параметры: Вь представляет собой показатель среднего сходства между МЗ и ДЗ близнецами; В2 — оценку удвоенной разницы между средними в группах МЗ и ДЗ близнецов (с учетом ковариации между значениями МЗ и ДЗ пробандов); В3 оценивает долю дисперсии, объясняемую сре-довыми влияниями, общими для членов близнецовой пары (VС /VР или С ); В4, отражает разницу h g - h2 , где h2 — коэффициент наследуемости в широком смысле и h g — коэффициент наследуемости в определенной группе (например, коэффициенты наследуемости IQ в группах здоровых людей и людей, страдающих ФКУ, отличаются друг от друга; В4 показывает разницу коэффициентов наследуемости, полученных в генеральной популяции и специфической выборке); и, наконец, В5 оценивает коэффициент наследуемости (h ), т. е. показатель того, насколько индивидуальные различия в исследуемой выборке объясняются наследуемыми влияниями.
Интересной особенностью ДФ-метода является то, что он позволяет тестировать гипотезу о сходстве или различии этиологии нормально распределенных и экстремальных значений. Сравнение регрессионных коэффициентов В2 и В5 позволяет проверить гипотезу о том, сходны ли этиологии девиантных и «средних» значений, например, по тесту на математические способности. Если этиология неспособности к математике отличается от этиологии средних математических способностей, то В2 и В5 должны статистически надежно отличаться друг от друга. Если же дети, которые имеют трудности в овладении математикой, представляют собой не отдельную группу, а край нормального распределения, то В2 и В5 статистически отличаться друг от друга не должны,
Разные формулы для вычисления коэффициентов наследуемости характеризуются разного рода допущениями и ограничениями. В нескольких исследованиях было продемонстрировано, что применение разных формул на одном и том же эмпирическом материале дает разные результаты. Поэтому интерпретация данных, полученных одним методом близнецов, должна проводиться с учетом всех ограничений, свойственных этому методу. Ф. Фогель и А. Мотульски [159] отмечают, что даже при сильно упрощающих допущениях (например, отсутствия ассортативности, доминирования и т.д.) все равно остаются систематические ошибки, которые невозможно полностью проконтролировать. Они рекомендуют вычислять из одних и тех же эмпирических данных альтернативные оценки и сравнивать, насколько хорошо они совпадают.
Метод приемных детей. При допущении, что среда семей-усыновителей не коррелирует со средой тех биологических семей, из которых данные дети усыновляются, корреляции детей с их биологичес-
201
кими родителями представляют собой «чистые» генетические корреляции (т.е. прямую оценку h2 или VG /VP, а с родителями-усыновителями — «чистые» средовые корреляции (с2 или VС /VP). Однако в том случае, если среды биологических и приемных семей похожи, допущение о «чистоте» полученных оценок генетической и средовой составляющих чаще всего неправомерно (по крайней мере в тех случаях, когда корреляция сред неизвестна). Методологически адекватным, хотя практически и не всегда возможным решением в подобной ситуации служит получение нескольких оценок генетического и средово-го компонентов при разных значениях корреляции сред.
Таким образом, главной причиной беспокойства при использовании метода приемных детей является допущение об отсутствии корреляции между биологическими и приемными семьями. Кроме того, исследователи должны убедиться в том, что семьи-усыновители репрезентативны общей популяции, т.е. не отличаются от среднепопуля-ционной семьи по уровню благосостояния, образования и т.п. Если семьи-усыновители нерепрезентативны, закономерности, полученные в результате их анализа, не могут считаться справедливыми для генеральной популяции.
АНАЛИЗ ПУТЕЙ
Приведенная выше логика разложения фенотипической дисперсии на ее составляющие, реализованная в нескольких эмпирических методах, представляет собой один из способов определения коэффициента наследуемости того или иного признака. Но понятие наследуемости можно также проанализировать при помощи «анализа путей».
Анализ путей в последние десятилетия широко используется и в психогенетике, и в науках о поведении вообще. Он был предложен генетиком С, Райтом еще в 30-х годах и затем им же и другими исследователями детально разработан. Четкое изложение его основ и правил использования содержится в упоминавшемся труде М. Нила и Л. Кардона [342], которые характеризуют этот метод следующим образом.
Диаграмма путей — эвристичный способ наглядного графического представления причинных и корреляционных связей (путей) между переменными, позволяющий дать полное математическое описание линейной модели, которую применяют исследователи. Тем самым диаграмма путей способствует ее пониманию, верификации или представлению результатов. В целом путевые модели — «экстремально обобщенный» способ анализа, один из многих мультивариативных методов (к ним же относятся методы множественной регрессии, факторный и дискриминантный анализы и т.д.).
Существуют определенные правила построения диаграмм путей (рис. 8.4). Прямоугольники (или квадраты) обозначают наблюда-
202
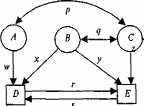
Рис. 8.4. Диаграмма путей, объединяющая три латентных (А, В, С) и две наблюдаемых (D и Е) переменных.
риq — корреляции; r, s, w, х, у, z — путевые коэффициенты.
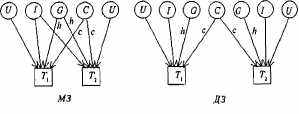
Рис. 8.5. Диаграмма путей для корреляций совместно живущих пар МЗ и ДЗ близнецов.
Th т2 — близнецы одной пары. G — генотип; С— общая среда; U — индивидуальная (уникальная) среда; I— эпистаз. Пути h, с — влияния G, С на исследуемую черту.
емые переменные; круги (или эллипсы) — латентные, неизмеряе-мые переменные (на рис. 8.4. D и Е; А, В, С соответственно).
Связи между переменными обозначаются стрелками: постулированные исследователем причинно-следственные — направленной в одну сторону («путь» от причины к следствию); наблюдаемые ассоциации — двусторонней. На рис. 8.4 первые — w, x, у, z, r, s (путевые коэффициенты); вторые — р и q (коэффициенты корреляции). Иначе говоря, модель выделяет зависимые переменные (D и Е), подлежащие объяснению или прогнозированию, и независимые (А, В, С), действие которых должно объяснить или предсказать зависимые переменные и их связи. Есть и другие, более детальные, правила оформления и чтения путевых диаграмм, но мы их рассматривать не будем.
На рис. 8.5 даны модели путей для корреляций совместно живущих пар МЗ и ДЗ близнецов по экстраверсии, из которых следует, что
203
корреляция МЗ близнецов T1 и Т2 может быть выражена через сумму путей, связывающих их, т.е. hh и сс; иначе говоря, rМЗ = h2 +с2 . Для ДЗ это будут пути h х 1/2 х h и cc, т.е. rДЗ = 1/2 h2 + с2 . Вычитая, получим rМЗ — rДЗ = h2 + с2 — 1/2 h2 — с2 = 1/2 h ; чтобы получить полную генетическую дисперсию (а не половину ее), удваиваем разность корреляций h2 = 2(rMЗ — rДЗ ) и получаем описанный выше коэффициент наследуемости, справедливый для близнецовых исследований. Аналогичным образом могут быть построены путевые диаграммы для семейных и любых других данных.
Единицы измерения, используемые в анализе путей, отличаются от тех, которыми мы оперировали тогда, когда рассматривали понятие наследуемости на примере разложения фенотипической дисперсии. Если при разложении дисперсии мы пользовались квадратичными единицами (например, h2 , VG ), то в данном случае наследуемость описывается на языке стандартных отклонений. Тогда путевые коэффициенты являются коэффициентами регрессии, полученными для переменных не в исходных единицах, а для стандартизованных переменных.
Несмотря на широкое использование этого метода и его достоинства, которые заключаются прежде всего в наглядной демонстрации представлений о компонентах, влияющих на исследуемый признак, он имеет и своих критиков. Так, Ф. Фогель и А. Мотульски «не уверены в том, что этот метод биометрического анализа внесет существенный вклад в наше понимание генетических факторов» [159]. Одно из главных сомнений вызывает тот факт, что в диаграмму путей и, следовательно, в дальнейший математический анализ закладываются уже имеющиеся у исследователя предположения о влияющих на признак факторах, их причинно-следственных отношениях и т.д., и результат анализа зависит, таким образом, от корректности заранее имеющихся исходных позиций.
АНАЛИЗ МНОЖЕСТВЕННЫХ ПЕРЕМЕННЫХ
До сих пор наши рассуждения концентрировались в основном на одном фенотипе, т.е. нашей конечной переменной являлся какой-то конкретно взятый фенотип. А если мы заинтересованы в одновременном изучении двух фенотипов, которые теоретически могут быть связаны между собой? Например, связана ли вариативность в популяции по таким высоко коррелирующим признакам, как вербальный и невербальный интеллект? Насколько вероятно предположение о том, что вариативность по этим двум признакам может быть объяснена действием одних и тех же генетических и средовых влияний? Иными словами, если два признака коррелируют на фенотипическом уровне, то эта корреляция может быть результатом действия как генетичес-
204
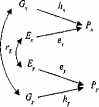
Рис. 8.6. Диаграмма путей фенотипической корреляции двух признаков Рх и Ру , демонстрирующая роль генетической rG и средовой rE составляющих.
ких, так и средовых факторов, и задача может заключаться в том, чтобы понять происхождение не только самих фенотипов, но и их корреляции.
Среди генетических причин, которые могут привести к появлению корреляции между признаками на фенотипическом уровне, следует указать на так называемый эффект плейотропии, или множественного влияния одних и тех же генов на разные признаки. Кроме того, различные популяционные процессы, например неслучайное скрещивание и смешивание популяций, также могут привести к возникновению корреляции между фенотипами.
Примером средового влияния на формирование фенотипической корреляции может служить дефицит питания: недоедающие дети обычно значительно ниже своих сверстников как по весу, так и по росту, т.е. связь этих двух характеристик обеспечивается одним средовым фактором.
Значимость такого рода одновременного моделирования множественных переменных трудно переоценить. Существуют целые классы поведенческих признаков, которые высоко коррелируют между собой (например, различные показатели когнитивной сферы, показатели эмоционально-волевой сферы и т.п.). Предположение о том, что вариативность по высоко коррелирующим психологическим признакам может объясняться действием одних и тех же генетических и/или средовых факторов кажется весьма правдоподобным.
Математическое описание множественных моделей достаточно просто, Рис. 8.6 представляет собой иллюстрацию того, как модель путей, рассмотренная нами, может быть разработана для одновременного анализа двух коррелирующих признаков. Подобно тому как фенотипическая вариативность отдельно взятого признака (Рх ) отражает вариативность генотипов (hх ) и сред (ex), фенотипическая корреляция между X и Y (rРх Ру ) может быть результатом набора генетических (hx hу rG) и средовых (ех еy RЕ) путей, где rG и rЕ представляют
205
собой генетическую и средовую корреляции, соответственно. В результате
rPxPf = hx hy r G + ех еy RЕ
