Федеральная программа книгоиздания России Рецензенты: канд психол наук С. А. Исайчев, доктор биол наук И. И. Полетаева Равич-Щербо И. В. и др. Р12

Вид материала

Программа

Содержание Метод контрольного близнеца Метод близнецовой пары. Статистические методы психогенетики Статистические методы психогенетики 1. Генетика количественных признаков и ее значение для психогенетики Модель одного гена Генотипическое значение. Аддитивное генотипическое значение. Доминантные отклонения.

Подобный материал:

• Вестник балтийской педагогической академии вып. 94. – 2010 г. Актуальные проблемы нравственного, 2431.92kb.
• Рецензенты: профессор, доктор психол наук Филонов Л. Б., вед науч сотрудник, канд психол, 2609.63kb.
• Научный выпуск вестник балтийской педагогической академии вып. 29. – 2000 г. Поиск, 1745.18kb.
• Общеобразовательная программа дошкольного образования Авторский коллектив, 5619.19kb.
• Образовательная программа дошкольного образования Москва «Просвещение», 5670.3kb.
• Введенским Игорем Витальевичем Рецензенты доктор психол наук В. А. Лабунская канд психол, 375.9kb.
• Отчет о проведении Международной научной конференции-семинара «Современные методы психологии», 97.76kb.
• Приглашение и программа разнообразие почв и биоты северной и центральной азии, 521.14kb.
• Пояснительная записка, 12621.4kb.
• В организации совместных отношений, 1137.14kb.

12*

179

Основное ограничение метода заключается в том, что генетичес­ки идентичные родители могут создавать в своих семьях сходную сре­ду, в которой взаимодействия в диадах ребенок Х МЗ родитель и ребе­нок Х МЗ дядя (тетя) будут весьма похожими, а у ДЗ родителей со своими детьми и племянниками будет такое же средовое и генетичес­кое сходство, как у родителей и детей в обычной семейной ситуации. Поэтому данный вариант близнецового метода может успешно ре­шать некоторые частные вопросы, однако для разделения генетичес­кой и средовой дисперсии признака он имеет меньшую разрешаю­щую способность, чем другие методы психогенетики [363].

Метод контрольного близнеца (взаимоконтроля близнецов, конт­роля по партнеру, близнеца-свидетеля) основан на том, что МЗ близ­нецы, — генетически одинаковые люди, имевшие общую эмбрио­нальную и в обычных условиях семейную среду, — являются идеаль­ным контролем друг к другу. Если группу МЗ близнецов разделить на две выборки так, чтобы в каждую вошли по одному близнецу из каж­дой пары, то исследователь получит уникальную ситуацию — две вы­борки, уравненные и по генетической конституции, и по основным средовым (общесемейным) параметрам. Далее можно, например, одну группу тренировать, а другую — нет или тренировать их в разном возрасте, как это было сделано в работе А. Гезелла, впервые приме­нившего данный метод и прослеживавшего вместе с коллегами раз­витие одной женской пары МЗ близнецов с первых месяцев жизни до 14 лет [272, 273, 274, 275]. Они получили материал, свидетельствую­щий о зависимости эффективности обучения (двигательного и рече­вого) от возраста. Одновременно можно оценить и длительность удер­жания эффекта тренировки: поскольку в раннем детстве созревание существенно определяется генетической программой, тип и темп его у МЗ близнецов в основном одинаковы. В упомянутых работах А. Гезел­ла и его сотрудников показано, например, что разница в речевом развитии, стимулированном тренировкой в возрасте 1,5-2 лет, стер­лась в течение трех месяцев.

Шведский исследователь А. Незлунд [цит. по: 434] оценил таким методом разные способы обучения чтению и показал, что одного, оптимального для всех способа нет, их эффективность зависит от уровня интеллектуального развития ребенка.

В упоминавшихся (см. Введение) работах Московского Медико-генетического института этот метод (5 пар МЗ близнецов 5-6 лет) тоже использован для анализа не только эффекта обучения, но и кон­структивной деятельности. Показано, что обучение при помощи ме­тода «моделей» эффективнее, чем простое копирование: не только улучшается сама конструктивная деятельность, но и перестраиваются другие психические функции ребенка. Позже, в 1956 г., была опубли­кована работа А.Р. Лурия и Ф.Н. Юдович о развитии речи, где МЗ близнецы также служили контролем друг к другу [ 102].

180

Р. Пломин с соавторами [363] отмечал, что таких работ очень мало — «менее дюжины», но и их, тем не менее, делят на три группы. В первую входят наиболее ранние работы, в которых исследуется вза­имодействие между созреванием и тренировкой, при этом близне­цов-партнеров обучают одному и тому же, но в разных возрастах. К дан­ной группе относятся, например, упоминавшиеся работы А. Гезелла с сотрудниками. Во второй группе работ сравнивается эффективность разных способов обучения, в качестве примера может служить упомя­нутое шведское исследование обучения чтению. Авторы третьей, наи­более обширной группы работ изучают вопрос о том, насколько существенными могут быть различия, создаваемые средой у генети­чески идентичных индивидуумов. Примером могут служить экспери­ментальные методы изменения средовых воздействий, использован­ные в упоминавшихся исследованиях Московского Медико-генети­ческого института.

Метод близнецовой пары. Еще в 30-х годах появились работы, в которых рассказывалось об особой психологической ситуации в парах близнецов, особом «эффекте пары», или «эффекте близнецовости». Они были выполнены и в психоаналитической традиции, и в психо­логии развития, и, специально, в русле психогенетических исследо­ваний. Основными характеристиками этой особой психологической ситуации являются две борющиеся тенденции: к идентификации со своим со-близнецом и, наоборот, к индивидуализации каждого члена пары. Первая приводит к ощущению себя сначала членом пары и лишь затем — отдельной личностью; вторая, в крайних случаях, может при­вести к выраженным конфликтным отношениям близнецов, своеоб­разному протесту против «второго — такого же». С возрастом первая тенденция обычно ослабевает, уступая место второй, причем у близ­нецов-мужчин данный процесс происходит легче, чем у женщин.

На этом фоне существуют более тонкие оттенки внутрипарных отношений. Например, еще в 1934 г. X. фон Браккен описал феномены гармонического и дисгармонического соперничества близнецов: «со­ревнование друг с другом» и «соревнование друг против друга». Сна­чала предполагалось, что первое характерно для МЗ близнецов, вто­рое — для ДЗ, однако в дальнейшем это не подтвердилось; оба типа диадических взаимодействий встречаются и у тех, и у других. Он опи­сал и некоторые специфические для пары социальные роли: «мини­стра внешних сношений», осуществляющего общение с внешним миром, и «министра внутренних дел» («совесть пары»). Позже ролевые отношения, существующие в повседневной жизни близнецов, были описаны итальянским исследователем Л. Геддой и другими зарубеж­ными авторами, а среди отечественных В.В. Семеновым [132, 137] и Н.В. Искольдским [65, 66]. Они же продемонстрировали, как распре­деление ролей влияет на оценку внутрипарного сходства и, соответ­ственно, на величину коэффициента наследуемости, о чем уже го-

181

ворилось ранее. А в работах И.И. Канаева [69, 70] было показано, как роли «старшего» (родившегося первым) и «младшего», ведущего и ве­домого, формируют различия в психологическом облике близнецов.

Однако наиболее детально близнецовую ситуацию исследовал Р. Заззо и описал в 1960 г. в книге «Близнецы: пара и личность» (на русский язык она, к сожалению, не переведена; краткий анализ см.: [152]). Он ввел и само понятие «близнецовая ситуация», показал ее проявления и обосновал необходимость ее изучения.

Сам Р. Заззо назвал исследование близнецовых пар «третьим мето­дом» наряду с методами «контрастных групп» Гальтона (имеется в виду сопоставление групп МЗ и ДЗ близнецов) и «контрольного близ­неца» Гезелла [459]. Согласно Р. Заззо, на фоне сходства близнецов, порождаемого и генетическим сходством и тем, которое формируется широкой средой, выделяется еще один фактор, создающий и специ­фическое сходство, и различия в глубине его, — близнецовая ситуа­ция, своеобразный «микрокосм», результатом действия которого мо­жет стать и конвергенция, и дивергенция развития.

С помощью этого варианта метода решаются две задачи. Первая из них — общепсихологическая: поскольку индивидуум существует только внутри некоторых систем связей (например, в диаде) и «в этом смыс­ле можно сказать, что мы все «близнецы»» [459, с. 25], постольку близнецовая пара, особенно генетически идентичные МЗ близнецы, может быть прекрасной моделью для изучения процессов индивидуа­лизации, влияния конкретных средовых (внутрипарных и семейных) факторов на формирование тех или иных психологических черт и т.д. Вторая задача по существу есть проверка, во-первых, валидности са­мого близнецового метода, а также постулата о равенстве средовых влияний в парах МЗ и ДЗ близнецов и, во-вторых, вопроса о том, репрезентативна ли среда близнецов среде, в которой развиваются одиночнорожденные дети. Если условия развития и жизни близнецов высоко специфичны, имеют собственные, только им присущие зако­номерности, то близнецы перестают быть выборкой, репрезентатив­ной общей популяции, и не могут быть использованы для изучения общих закономерностей.

К двум указанным задачам необходимо, на наш взгляд, добавить третью, связанную с жизнью самих близнецов. Чрезмерная, не ком­пенсируемая идентификация себя со своим со-близнецом, или пары как целого, как особой «единицы», приводящая к отсутствию личной идентичности, может стать причиной формирования личностных черт, затрудняющих социальную адаптацию и в детстве, и во взрослом воз­расте. Кроме того, отмеченные еще Р. Заззо и затем А. Р. Лурия особен­ности речевого развития близнецов, точнее формирование прими­тивной, синпрактической речи («криптофазия», по Заззо), может привести к отставанию и в общем интеллектуальном развитии [см.: 97]. Поэтому изучение специфических психологических характеристик

182

близнецовой пары необходимо и для проведения консультационной работы с родителями, имеющими детей-близнецов.

* * *

Методы, которыми располагает психогенетика, позволяют весьма надежно решать ее главную задачу: выяснение той роли, которую иг­рают факторы наследственности и среды в формировании межинди­видуальной вариативности психологических и психофизиологических признаков, индивидуальных траекторий развития и т.д. Особенно це­нен имеющийся в литературе анализ ограничений каждого метода, который позволяет либо контролировать помехи, либо компенсиро­вать их объединением разных методов. Это — обязательное условие продуктивного развития любой точной науки.

Кроме того, методы психогенетики позволяют более надежно ре­шать ряд негенетических задач, связанных с выделением актуальных для различных психологических черт средовых переменных, с более точной оценкой эффектов внешних воздействий и многих других.

Глава VIII

СТАТИСТИЧЕСКИЕ МЕТОДЫ ПСИХОГЕНЕТИКИ

Образно говоря, статистика является «правой рукой» психогене­тики. Как уже отмечалось, психогенетика изучает вопросы наследова­ния поведенческих признаков и психологических функций в популя­циях, и по определению эта наука озабочена не отдельными индиви­дуальностями, а их разнообразием, т.е. популяционной изменчивостью (вариативностью, дисперсией) изучаемого признака. Иными слова­ми, психогенетику интересуют вопросы, касающиеся характеристик распределений (среднего, дисперсии и других моментов распределе­ния) индивидуальных значений по изучаемому признаку в популя­ции, а также вопросы о том, влиянием каких факторов — генетичес­ких или средовых — можно объяснить наблюдаемую изменчивость. Статистики, описывающие параметры популяции (выборки), приво­дятся в любом руководстве по статистике, поэтому здесь мы их ка­саться не будем, а перейдем сразу к статистическим решениям соб­ственно психогенетических задач.

Как уже говорилось, психологические признаки принадлежат к классу количественных признаков, законы наследования которых су­щественно отличаются от менделевских. Особая здесь и статистика. Последовательно рассмотрим связанные с этим вопросы.

183

близнецовой пары необходимо и для проведения консультационной работы с родителями, имеющими детей-близнецов.

* * *

Методы, которыми располагает психогенетика, позволяют весьма надежно решать ее главную задачу: выяснение той роли, которую иг­рают факторы наследственности и среды в формировании межинди­видуальной вариативности психологических и психофизиологических признаков, индивидуальных траекторий развития и т.д. Особенно це­нен имеющийся в литературе анализ ограничений каждого метода, который позволяет либо контролировать помехи, либо компенсиро­вать их объединением разных методов. Это — обязательное условие продуктивного развития любой точной науки.

Кроме того, методы психогенетики позволяют более надежно ре­шать ряд негенетических задач, связанных с выделением актуальных для различных психологических черт средовых переменных, с более точной оценкой эффектов внешних воздействий и многих других.

Глава VIII

СТАТИСТИЧЕСКИЕ МЕТОДЫ ПСИХОГЕНЕТИКИ

Образно говоря, статистика является «правой рукой» психогене­тики. Как уже отмечалось, психогенетика изучает вопросы наследова­ния поведенческих признаков и психологических функций в популя­циях, и по определению эта наука озабочена не отдельными индиви­дуальностями, а их разнообразием, т.е. популяционной изменчивостью (вариативностью, дисперсией) изучаемого признака. Иными слова­ми, психогенетику интересуют вопросы, касающиеся характеристик распределений (среднего, дисперсии и других моментов распределе­ния) индивидуальных значений по изучаемому признаку в популя­ции, а также вопросы о том, влиянием каких факторов — генетичес­ких или средовых — можно объяснить наблюдаемую изменчивость. Статистики, описывающие параметры популяции (выборки), приво­дятся в любом руководстве по статистике, поэтому здесь мы их ка­саться не будем, а перейдем сразу к статистическим решениям соб­ственно психогенетических задач.

Как уже говорилось, психологические признаки принадлежат к классу количественных признаков, законы наследования которых су­щественно отличаются от менделевских. Особая здесь и статистика. Последовательно рассмотрим связанные с этим вопросы.

183

1. ГЕНЕТИКА КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ И ЕЕ ЗНАЧЕНИЕ ДЛЯ ПСИХОГЕНЕТИКИ

Генетика количественных признаков предоставляет психогенети­ке общую теорию, на базе которой строится методологический аппа­рат изучения природы индивидуальных психологических различий.

В самом общем виде генетика количественных признаков — при­менительно к психологическим задачам — исходит из того, что люди отличаются друг от друга по ряду сложных психологических призна­ков, и предлагает модель, в рамках которой межиндивидуальные раз­личия по этим признакам могут быть описаны в терминах фенотипи-ческой дисперсии признака в популяции, а сама стенотипическая дис­персия может быть разложена на составляющие ее генетические и средовые компоненты.

МОДЕЛЬ ОДНОГО ГЕНА

Количественные генетические модели позволяют описать измеря­емые эффекты различных генотипов, возможных в отдельно взятом локусе, и суммировать эффекты всех локусов, контролирующих тот или иной поведенческий признак. Причем количество локусов, конт­ролирующих данный признак, обычно неизвестно, и чаще всего уче­ные делают допущение о том, что генетический контроль большин­ства поведенческих признаков осуществляется большим количеством генов, вклад которых в дисперсию изучаемого признака примерно одинаков. Одним из характерных признаков количественных генети­ческих моделей является то, что они предполагают существование нормально распределенных фенотипических значений признаков, контролируемых множеством генов, эффекты которых, в свою оче­редь, опосредованы средовыми влияниями. Многолетние психологи­ческие исследования показали, что распределение большинства по­веденческих признаков действительно соответствует нормальной кри­вой. Поэтому допущение о нормальности распределения признака, контролируемого большим количеством генов и значимых средовых влияний (т.е. являющегося мультифакторным), — психологически адек­ватная и статистически удобная модель для психогенетики. Важно за­метить, что ожидаемая от полигенной системы нормальность распре­деления, будучи статистически удобной и эмпирически оправданной, не зависит от количества генов, контролирующих эту систему. Как статистические характеристики, так и теоретические положения, ле­жащие в основе моделей количественной генетики, одинаково пра­вомерны для моделей, содержащих 1, 2, 25 или более генов. Именно поэтому мы начнем изложение основных признаков количественной генетики с рассмотрения модели одного гена и только потом перейдем к модели множественных генов (так называемой полигенной модели).

184

Аа аа__________________+------->___________АА

Рис. 8.1. Соотношение трех генотипов, возможных для двуаллельной сис­темы.

Параметры d и h представляют собой разницы эффектов генов А-а. Аа может нахо­диться на любой из сторон от т, что, соответственно, будет влиять на знак h. В примере, показанном па рисунке, значение h положительно [253, 342].

Генотипическое значение. Генотипическим значением называется некоторое количественное значение, приписываемое определенному генотипу. Так, в рамках простейшей двуаллельной системы (А и а) существуют два параметра, определяющие измеряемые эффекты трех возможных генотипов (АА, Аа и аа). Этими параметрами являются параметр d, представляющий собой удвоенную разницу между гомо­зиготами АА и аа, и параметр h, определяющий измеряемый эффект гетерозиготы Аа таким образом, что он не является точным усреднен­ным эффектом двух гомозигот, Средняя точка между двумя гомозиго­тами, точка т, отражает среднее эффектов двух гомозиготных геноти­пов. Параметры d и h называются эффектами генотипов. Графически соотношение трех генотипов показано на рис. 8.1. Если в локусе отсут­ствует доминантность, то h будет равняться нулю, а значение геноти­па Аа будет соответствовать значению в точке т. При полной доми­нантности значение Аа будет равняться значению АА. Если же доми­нантность А частичка, то Аа будет находиться ближе к точке АА (или аа, в зависимости от направления доминантности) и значение h бу­дет положительным.

Приведем пример. Предположим, что известны гены, которые влияют на вес человека. Предположим также, что нормальный вес женщин среднего ро­ста составляет 48-70 кг, т.е. разница между максимальным и минимальным значениями по весу равна 22 кг. Теперь предположим, что гены, контролирую­щие вариативность веса человека, расположены на каждой из 22 аутосомных хромосом (по одному на каждой), причем все гены вызывают примерно одина­ковые эффекты. Тогда в рамках нашей гипотетической системы гомозиготы по каждому из изучаемых генов вкладывают примерно ± 1/2 кг (от средней точки), в зависимости оттого, являются они гомозиготами по аллелям, обозначаемым заглавной буквой (АА, ВВ, СС и т.д. - обладание этими генотипами повышает рост), или гомозиготами по аллелям, обозначаемым строчными буквами (аа, bb, ее и т.д. - обладание этими генотипами понижает рост). Рассмотренный при­мер, однако, невероятен по крайней мере по двум причинам: во-первых, генов, контролирующих вариативность веса человека, мы не знаем и, во-вторых, в ре­альной ситуации вклады генотипов, скорее всего, будут меньше или больше, чем 1/2 кг, затрудняя подсчет генотипического значения.

185

Модели генетики количественных признаков, во всяком случае в их классическом варианте, не являются ни средством идентификации конкретных генов, контролирующих вариативность признака, ни сред­ством точного определения вклада каждого генотипа. Эти модели ре­шают другую задачу, а именно задачу определения общего вклада генотипа в вариативность изучаемого признака в популяции.

Аддитивное генотипическое значение. «Аддитивное генотипическое значение» представляет собой фундаментальное понятие количествен­ной генетики, поскольку оно отражает, насколько генотип «истинно наследуется». Аддитивный (суммарный) эффект генов представляет собой не что иное, как сумму эффектов отдельных аллелей. Более точно, аддитивное генотипическое значение есть генотипическое зна­чение, обусловленное действием отдельных аллелей данного локуса. Генная доза генотипа подсчитывается на основе того, сколько алле­лей определенного типа (например, аллелей А) присутствует в дан­ном генотипе. Если наличие определенного аллеля в генотипе увели­чивается на 1 (как это происходит, например, в случае перехода от генотипа аа к генотипу Aа), то аддитивное значение увеличивается на некоторую определенную величину. На рис. 8.2 дана графическая иллюстрация аддитивного генотипического значения при отсутствии доминантности. Эффект генотипа аа = -d, поэтому эффект аллеля (гена) а = 1/2(—d); эффект генотипа АА = d, поэтому эффект аллеля А = 1/2(d); соответственно, эффект генотипа Аа = 1/2(d) + 1/2(-d) = 0. Заметим, что аддитивные генные значения зависят от частоты встречаемости аллелей в популяции. При отсутствии доминирования аддитивный эффект полностью определяет генотипическое значение. Доминантность, однако, вносит самые разные отклонения от ожида­емых значений, — об этом пойдет речь ниже.

Теперь допустим, что каждый аллель генотипа имеет некоторый средний эффект. В этом смысле аддитивное генотипическое значение

представляет собой сумму сред­них эффектов каждого аллеля для всех аллелей, входящих в гено-' тип. Каждый аллель характеризу-

' ется определенным аддитивным

¹ эффектом, соответственно, при

t унаследовании определенного ал-

\ леля от родителя ребенок насле-

j дует и аддитивный эффект этого

j_____ аллеля, т.е. вклад аллеля в гено­тип ребенка будет таким же, ка-

Рис. 8.2. При отсутствии доминант- ким был его (аллеля) вклад в ге-

ности (h = 0) аддитивное генотипи нотип родителя. И неважно,

ческое значение определяется генной сколько (много или мало) алле-

дозой. лей присутствует в данном локу-

186





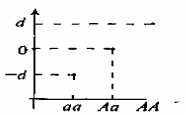
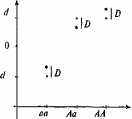
Рис. 8.3. Графическое изображение доминантных отклонений.

Наличие доминантности вносит разного рода изменения в аддитивное гепотипи-ческое значение.

Обозначения: • — аддитивные генотипические значения при условии полной до­минантности; * — наблюдаемые аддитивные значения, определяемые на основе генных доз; D — доминантные отклонения, которые представляют собой разницу между ожидаемыми аддитивными значениями, соответствующими ситуации пол­ной доминантности, и значениями, наблюдаемыми для определенных генных доз.

се или сколько локусов вовлечено в контроль вариативности по тому или другому признаку. Иными словами, аддитивное генотипическое значение представляет собой не что иное, как сумму вкладов каждого аллеля в генотип.

Доминантные отклонения. Доминантные отклонения есть мера того, насколько генотип отличается от своего ожидаемого аддитивного зна­чения.

Доминантные отклонения (рис. 8.3) — это разница между ожида­емыми и наблюдаемыми значениями генотипов. Феномен доминант­ности допускает, что два аллеля одного локуса могут взаимодейство­вать друг с другом и тем самым менять генотипическое значение, которое наблюдалось бы в том случае, если бы они были независимы друг от друга и делали независимые вклады в генотипическое значе­ние. Так, в результате взаимодействия аллелей Аа наблюдаемое гено­типическое значение меньше того, которое ожидалось бы при усло­вии полной доминантности. Напротив, значения АА и аа выше ожи­даемых при допущении, что аллель А полностью доминантен по отношению к аллелю а.

Доминантность обязана своим возникновением уникальному со­четанию аллелей в данном локусе. Очевидно, что генотип потомка, наследующего только один аллель от каждого из родителей, в подав­ляющем большинстве случаев не может воспроизвести уникальность генотипа одного из них. Поэтому потомки будут отличаться от своих родителей в той мере, в какой аллели данного локуса не суммируются линейным образом при определении генотипического значения.

187

Рассмотрев типы генетических влияний, определим, как частоты встречаемости аллелей, определяющие эти типы, задают среднее зна­чение генотипа в популяции. Допустим, что в популяции аллели А и а встречаются с частотами р и q, соответственно. Тогда первая колонка в табл. 8.1 показывает три возможных генотипа, вторая — частоты их встре­чаемости в популяции (при допущении, что особи в этой популяции образуют родительские пары случайным образом) и третья — значение генотипа. Популяционное среднее получается путем умножения значений генотипа на частоту встречаемости тех аллелей, которые этот генотип составляют, и последующего суммирования значений все трех генотипов.

Таблица 8.1