Редакционная коллегия: И. Н. Коробкова, Т. Л. Ржаницына, М. В. Чуприна Практико-ориентированное обучение: проблемы и перспективы

Вид материала

Документы

Содержание Белова О.В. Сумцова Л.Д. Остапенко Н.А Выдрина Е.О. Моляка А.С. Жилина Н.В. Арефьева Т.Г. Дербина Т.А. Закутаева Н.В. Реализация прикладной направленности I уровень. II уровень III уровень М. Дудин) Практико-ориентированных заданий в преподавании математики Применение практических методов обучения в преподавании права Дидактические игры Практико-ориентированный подход Необходимость и возможности практико-ориентированного обучения студентов экономических специальностей колледжа Затраты на достижение соответствия качеству, в т.ч. ... Полное содержание

Подобный материал:

• Личностно-ориентированное обучение личностно-ориентированное обучение, 37kb.
• Редакционная коллегия: Т. Б. Мильруд (гл ред.), С. Д. Дробышевская (составитель) Скажи, 613.91kb.
• «Личностно-ориентированное обучение – средство формирования познавательной активности, 139.21kb.
• План -конспект урока английского языка в 3 классе (второй год обучения) «Рождество, 143.83kb.
• Урок. Тема: "Биография", 39.9kb.
• Ю. А. Проблемы формирования «успешного» педагога в системе постдиплом, 201.91kb.
• Ю. А. Проблемы формирования «успешного» педагога в системе постдиплом, 201.87kb.
• Реализация личностно-ориентированного обучения в преподавании основных предметов, 176.32kb.
• Е. Ю. Прокофьева редакционная коллегия, 868.19kb.
• Е. Ю. Прокофьева редакционная коллегия, 7181.6kb.

Федеральное государственное образовательное учреждение среднего профессионального образования

«Омский авиационный колледж имени Н.Е Жуковского»


ПРАКТИКО-ОРИЕНТИРОВАННОЕ ОБУЧЕНИЕ:

ПРОБЛЕМЫ И ПЕРСПЕКТИВЫ


Материалы научно-практической конференции преподавателей


Омск, 18 мая 2011 года


Омск

2011

Редакционная коллегия: И.Н. Коробкова, Т.Л. Ржаницына, М.В. Чуприна


Практико-ориентированное обучение: проблемы и перспективы. Материалы научно-практической конференции (18 мая 2011г.). – Омск, 2011. - 84с.


В сборнике представлены материалы научно-практической конференции, отражающие идеи и опыт использования практико-ориентированного подхода в учебном процессе образовательного учреждения. Сборник содержит статьи преподавателей федерального государственного образовательного учреждения среднего профессионального образования «Омский авиационный колледж имени Н.Е Жуковского».

СОДЕРЖАНИЕ

Секция 1
Белова О.В. Реализация прикладной направленности курса математики в колледже (из опыта работы преподавателя математики)_______________________	5
Сумцова Л.Д. Использование практико-ориентированных заданий в преподавании математики	16
Жаворонкова Я.В. Применение практических методов обучения в преподавании права____________________	20
Остапенко Н.А. Практико-ориентированный подход в преподавании дисциплины «Безопасность жизнедеятельности»_____________________________	25
Выдрина Е.О. Необходимость и возможности практико-ориентированного обучения студентов экономических специальностей колледжа___________	28
Моляка А.С. Деятельностно-компетентностный подход в практико-ориентированном обучении______	32
Чуприна М.В. Развитие базовых социальных компетенций у студентов в процессе изучения правовых дисциплин____________________________	39
Секция 2
Жилина Н.В. К вопросу об использовании практико-ориентированных заданий на факультативе по физике	44
Пашкова И.С., Шрейнер И.Ю. Методическое обеспечение уроков информатики с использованием практико-ориентированных подходов______________	52
Арефьева Т.Г. Практико-ориентированное обучение в преподавании истории (авторская редакция)________	58
Ковалев Н.Г. Организация самостоятельной работы студентов колледжа с использованием рабочей тетради в процессе изучения ОБЖ_________________	61
Дербина Т.А. Организация социального партнерства в колледже (из опыта организации практики студентов)	65
Горобцов А.В. Физическая культура студента колледжа: реалии и перспективы__________________	69
Закутаева Н.В. Применение активных методов обучения на факультативе «Полезная практика: реальные альтернативы» в колледже	72

Секция 1


РЕАЛИЗАЦИЯ ПРИКЛАДНОЙ НАПРАВЛЕННОСТИ

КУРСА МАТЕМАТИКИ В КОЛЛЕДЖЕ

(из опыта работы преподавателя математики)


О.В. Белова,

преподаватель математики


В настоящее время система образования ставит своей главной целью подготовку для общества квалифицированных специалистов. В образовательном процессе каждая учебная дисциплина создает предпосылки для формирования у студентов ключевых компетенций: ценностно-смысловой, общекультурной, учебно-познавательной, информационной, коммуникативной. Компетенции формируются в процессе деятельности и ради будущей профессиональной деятельности. В этих условиях процесс обучения приобретает новый смысл, он превращается в процесс учения/научения, то есть процесс приобретения знаний, умений, навыков и опыта деятельности.

Современный этап развития науки характеризуется взаимопроникновением наук, а межпредметные связи способствуют формированию понятий внутри отдельных предметов, групп и систем, полное представление о которых невозможно передать в рамках одной учебной дисциплины. Кроме того, это позволяет применять их в конкретных ситуациях, при рассмотрении частных вопросов в учебной и внеучебной деятельности.

Образовательные стандарты третьего поколения (технического профиля) отводят особую роль математике как одной из фундаментальных наук, а профессиональная направленность обучения позволяет рассматривать математику, во-первых, как средство, с помощью которого можно спроектировать процесс профильно-ориентированного обучения, во-вторых, как форму специфической межпредметной взаимосвязи общеобразовательных и профессиональных знаний.

Роль и значение математики в развитии межпредметных связей и формировании у студентов навыков практической деятельности рассматриваются в работах М.Б. Балка, Б.В. Гнеденко, В.А. Гусева, А.Г. Мордковича, А.В. Усовой и других. Анализ работ перечисленных авторов позволяет сделать вывод о том, что эта связь осуществляется за счет прикладной направленности математики. При этом основным носителем такой направленности являются практико-ориентированные задачи (Е.В. Величко, И.М. Шапиро и др.). Именно поэтому межпредметные связи являются важным условием и результатом комплексного подхода в обучении студентов.

По мнению Е.Н. Эрентраунт, реализация прикладной направленности математики должна учитывать комплекс дидактических принципов[4]:

1. методологической преемственности (формирование системы определенных способов и приемов, применяемых в научной сфере);

2. содержательной преемственности (включение материала, связанного с потребностями студентов в их дальнейшей учебе);

3. методической преемственности (включение способов деятельности, приближенных к тем, которые требуются в реальной действительности);

4. дифференциации и индивидуализации (учет характерных для студентов особенностей процесса усвоения).

Рабочие программы по математике содержат учебный материал, связанный с будущей профессиональной деятельностью студентов. Следует отметить, что содержание учебников по математике соответствует первому, второму и четвертому дидактическим принципам в них есть необходимый объём теории и практических заданий, часть из которых ориентированы на связь с профессией. Однако ни один учебник не может раскрыть все многообразие связей обучения с действительностью, поэтому кроме предлагаемых в учебнике систем упражнений необходимо использовать дополнительные задачи (приложение 1).

Любое занятие геометрии должно быть подтверждено наглядностью. Например, при изучении темы «Перпендикулярность прямой и плоскости» можно использовать иллюстрации Пизанской башни и развалин Древней Греции, обращая внимание студентов на дату, качество и надежность этих сооружений (приложение 2).

Обобщающий урок по теме «Вычисление объёмов геометрических тел» можно провести в форме презентации проектов «Определение комфортности жилья» (избушка, русский дом, восточный чум, яранга Аляски, монгольская юрта). Для выполнения проектов необходимо проанализировать форму жилья, традиции народа, определить комфортность жилья по формуле K=36πV2/S3 и, возможно, предложить свое альтернативное решение (приложение 3).

Занятия с использованием заданий прикладного характера можно обогатить, включив в их число следующие разновидности задач, предложенные И.М. Шапиро[2]:

- вычисление значений величин, встречающихся в практической деятельности (приложение 4);

- составление и чтение расчетных таблиц (приложение 5);

- построение простейших номограмм (приложение 6);

- применение и обоснование эмпирических формул;

- вывод зависимостей, встречающихся в практике.

Задачи с практическим содержанием можно применять на разных этапах урока. Использование таких задач в качестве средства мотивации создает условия для реализации связей математики с жизнью. Например, на одном из занятий студентам предлагается решить задачи трех уровней.

I уровень. Тело с высоты 20 м брошено вертикально вверх с начальной скоростью 50 м/с. В какой момент времени скорость изменения высоты тела равна нулю? Чему равна при этом высота тела над поверхностью земли?

II уровень. Лестница длиной 5 м приставлена к стене таким образом, что верхний конец находится на высоте 4 м. В некоторый момент лестница начинает падать, при этом верхний конец приближается к поверхности земли с постоянным ускорением 2 м/с. С какой скоростью удаляется от стены нижний конец лестницы в тот момент, когда верхний конец находится на высоте 2 м?

III уровень. Осветительная ракета запускается вертикально вверх с поверхности Земли и движется по закону h(t)=80t-4t. Труба высотой 40 м находится в 18 м от места запуска. Найдите: а) скорость изменения длины тени трубы в тот момент, когда длина тени трубы равна 10 м; б) скорость удлинения тени в момент, когда от ракеты до поверхности Земли остается 256 м? [1]

Анализ содержания задач показывает, что при решении первой задачи студенты овладевают умениями и навыками, необходимыми для успешного изучения разделов курса математики. Вторая задача направлена на выработку умения интегрировать знания разных тем. Для решения третьей задачи необходим творческий подход. Упражнения такого типа используются для организации индивидуальной работы на занятиях.

Таким образом, умения и навыки, приобретенные студентами при решении подобных задач, позволяют им самостоятельно выполнять задания прикладного характера, анализировать результаты, что, несомненно, важно в процессе реализации практико-ориентированного обучения математике. Для того чтобы студент усвоил учебный материал, необходимо, чтобы содержание задания стало целью его деятельности на занятии.


Литература

1. Саакян, С.М., Гольдман, А.М. Задачи по алгебре и началам анализа [Текст]: Пособие для учащихся 10-11 кл./С.М. Саакян, А.М. Гольдман. - М.: Просвещение, 2003. - 286с.
   
2. Шапиро, И.М. Использование задач с практическим содержанием в преподавании математики [Текст]: Книга для учителя / И.М. Шапиро. –М.: Просвещение, 1990. - 96с.
   
3. Федорец, Г.Ф. Межпредметные связи в процессе обучения [Текст] / Г.Ф. Шапиро. - М.: Наука, 1985. - 220с.
   
4. Эрентраунт, Е.Н. Обучение учащихся решению практико-ориентированных задач на старшей ступени профильной школы [Текст] / Е.Н. Эрентраунт. - МКО, - 2006. - Т. 1. - 250 [1] с. - С. 35 -40.
   

ПРИЛОЖЕНИЯ

Приложение 1


Физика, экология. Радиоактивные вещества


Огромную опасность для природы нашей планеты представляет гонка вооружений. Загрязнения, возникающие при испытании ядерного оружия, дают 1/5 всех загрязнений окружающей среды. Наша планета постепенно превращается в кладбище ядерных отходов. Так ли они безобидны? Скорость уменьшения массы m(t) радиоактивного вещества пропорциональна его количеству, т.е. m'(t) = – k m(t). Решением этого уравнения при t = 0 является m(t) = m₀e^–kt, где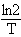, m₀  – масса вещества в начальный момент времени t = 0, m – масса вещества в момент времени t, Т – период полураспада. е ~ 2,718281828…, ln 2 ~ 0, 693147, ln 10 ~ 2,302585.

Период полураспада Т – это время, за которое первоначальная масса радиоактивного вещества уменьшится вдвое.

Периоды полураспада различных веществ неодинаковы: от миллиардов лет до десятимиллионных долей секунды.

Например, период полураспада урана от 238 до 4,5 млрд лет, цезия от 137 до 31 года, йода от 131 до 8 суток, тория всего с 3 • 10^–7 секунд.

Задача. Период полураспада радия равен 1600 годам. Через какое время его количество уменьшится в 10 раз?

Ответ: через 5315 лет количество радия уменьшится в 10 раз.

Через какое время из 1 кг радиоактивного радия получится 1 грамм? (Чтобы из 1 кг радиоактивного радия получить1 грамм необходимо 15945 лет).

Берегите
Жаворонка в голубом зените,
Бабочку на листьях повилики,
На тропинке солнечные блики,
На камнях играющего краба,
На могиле тень от баобаба,
Ястреба, парящего над полем,
Полумесяц над речным покоем,
Ласточку, мелькающую в жите,
Берегите Землю!
Берегите! ( М. Дудин)


Математические вычисления применяются и в естественных науках.

Биология. Размножение бактерий

Бактерии необычайно живучи. Их удается обнаружить в верхних слоях атмосферы на высоте нескольких десятков километров и глубоких подземных скважинах, в кипящих вулканических источниках и в толще антарктических ледников. Бактерии были найдены даже в воде, охлаждающей ядерные реакторы, т. е. там, где уровень радиации во много раз превышает смертельную дозу для человека. Оптимальная температура роста бактерий 30^o-40^o С. Встречаются виды, развивающиеся при температуре ниже 12^oС и выше 50^oС.

Задача. Скорость m'(t) размножения бактерий связана с массой m(t) бактерий в момент времени t уравнением m'(t) = km'(t), где k – положительное число, зависящее от  вида бактерий и внешних условий.

Решением этого дифференциального уравнения являются функции m(t) = Ce^kt
Если в  момент времени t = 0 масса бактерий – m₀, то m(t) = m₀e^kt

Какое потомство даст одна бактериальная клетка за 6 часов? (Коэффициент k = 2)

Ответ: 150000 бактерий – потомство одной бактериальной клетки за 6 часов.

Обратите внимание на формулы, используемые в 1 и 2 задачах. Чем они отличаются и как отражается это отличие на практике?

Формулы в задачах 1 и 2 отличаются знаком перед коэффициентом k. На практике это означает, что с течением времени количество радиоактивного вещества уменьшается, а численность бактерий увеличивается.


Приложение2




Приложение 3

Монгольская юрта. Высота верхнего конуса 2 м, цилиндра - 1.5 м, радиус юрты 4 м. Определить коэффициент комфортности жилья
Восточносибирский чум. Высота жилища - 4м, радиус - 3м. Определить коэффициент комфортности жилья.
Яранга эскимосов Аляски. Высота жилища 4м, радиус - 4м. Определить коэффициент комфортности жилья.
Русский дом. Высота 6м, ширина 4м, длина 3м. Определить коэффициент комфортности жилья, учитывая, что крыша не является жилым помещением.
Избушка. Высота 4м, ширина 4м, длина 4м. Определить коэффициент комфортности жилья, учитывая, что крыша не является жилым помещением.

Приложение 4


Введению показательной функции на моих уроках предшествовали следующие задачи:


1. К концу истекшего года было выпущено 840 000 автомобилей. Ежегодный прирост выпуска автомобилей составлял 10%. Сколько автомобилей будет выпущено в следующем году? Через 2 года? Через 5 лет? Через сколько лет выпуск автомобилей удвоится?

Результат: функция А(t)= 840000* 1,1


2. Рабочий положил в сбербанк 1000 рублей. Сбербанк начисляет ежегодно 2%. Сколько денег на сберкнижке будет через 5 лет? Через 10 лет?

Результат: функция D(t)= 100*1,02.

В итоге обобщения получили функцию вида y=ca


Приложение 5


На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали - температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев, когда среднемесячная температура не превышала 4 градусов Цельсия.





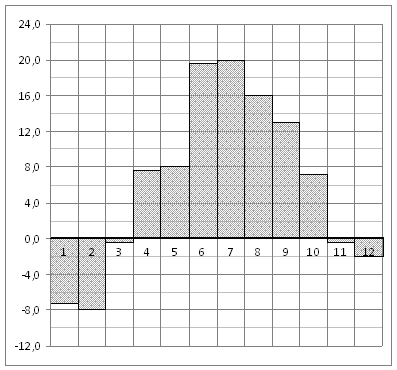
Приложение 6


На дно колодца опустили две палки длиной 2 м и 3 м так, что они пересекаются. Расстояние от их пересечения до дна составляет 1 м. Найти диаметр основания.

Решение: находим корень уравнения




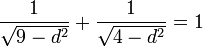
Если продлить меньшую диагональ трапеции до пересечения с прямой, параллельной дну колодца по исходящей от точки касания стены колодца и большой палки, то получаем отрезок длиной, равной произведению дна на уменьшенную на один боковую стенку. Это есть номограмма, в которой после задания отрезка единичной д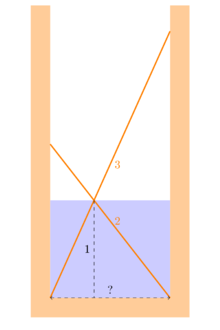лины можно найти результат произведения, деления и степени числа.


Приложение 7

Необходимо проложить водопроводную трубу от дома А к дому В. Стоимость прокладки трубы под асфальтом дороги-6000 рублей, а в любом другом месте-3600 рублей за метр. Как экономичнее проложить трубу? (На рисунке отражены все необходимые данные).





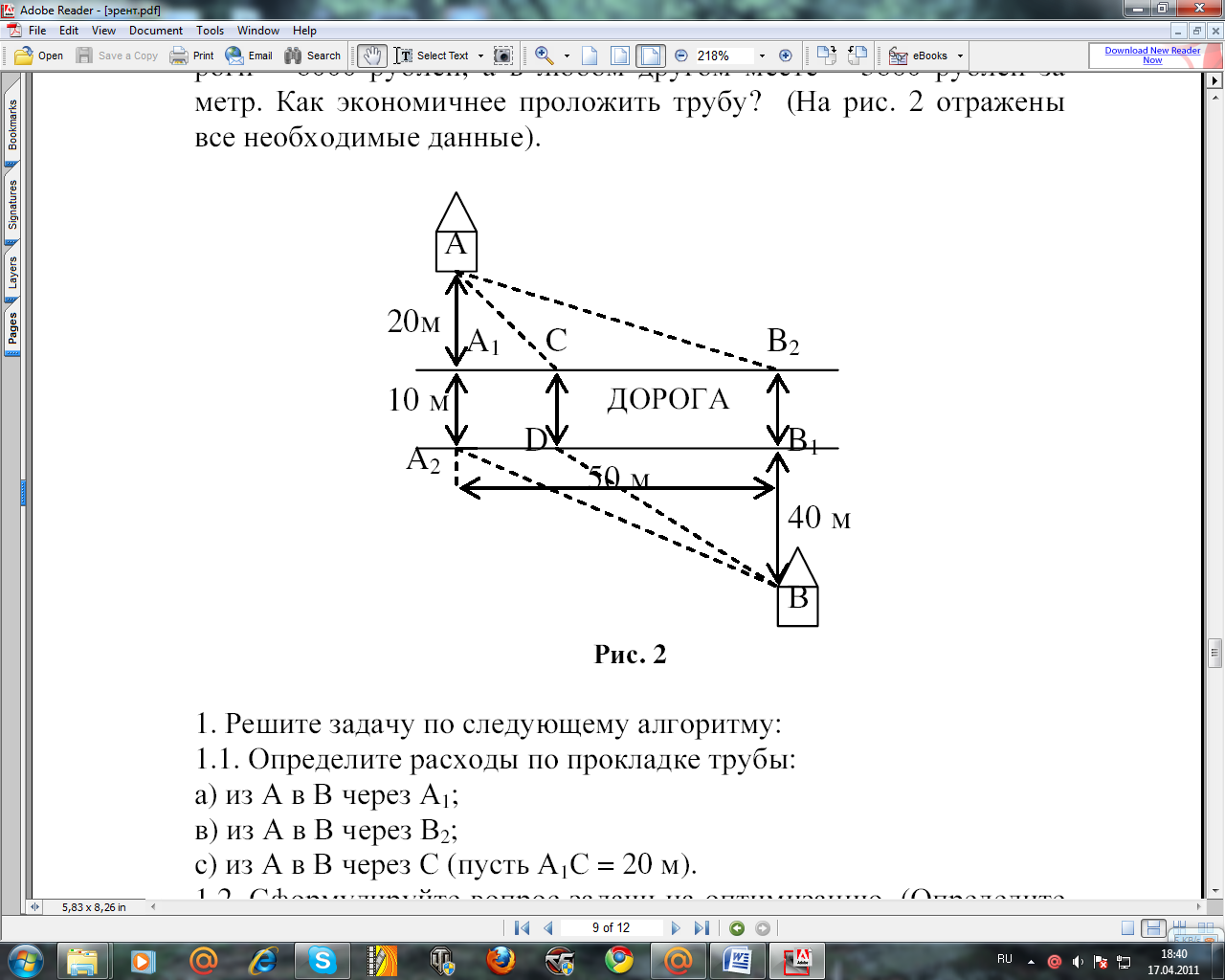
Определить расходы по прокладке трубы, решить вопрос задачи на оптимизацию; составить функцию, отражающую затраты по прокладке трубы; исследовать на экстремум.


ИСПОЛЬЗОВАНИЕ

ПРАКТИКО-ОРИЕНТИРОВАННЫХ ЗАДАНИЙ В ПРЕПОДАВАНИИ МАТЕМАТИКИ


Л.Д. Сумцова,

преподаватель математики


Реальная жизнь ставит перед выпускниками учебных заведений непростую задачу - быть востребованными на рынке труда. Любому производству требуются профессионалы, умеющие комплексно решать производственные задачи. Современная система образования предполагает развитие у студентов самостоятельности, мобильности, творческого мышления, необходимых для адаптации и продуктивной деятельности в различных профессиональных сферах.

Одной из задач цикловой методической комиссии математики и информатики является развитие у студентов новых способов мышления и деятельности. Рассмотрим один из методов практико-ориентированного преподавания математики, который основан на использовании некоторых психологических связей человека с производственным процессом. Элементы этого метода используются при изучении некоторых тем по геометрии.

Исторический анализ развития деятельности человека показывает, что главной его целью всегда было производство материальных благ, поэтому психика человека веками формировалась преимущественно под воздействием производственной деятельности. Посредством психологического механизма интериоризации она сформировала в коре головного мозга человека определенные устойчивые связи, ставшие наследственными программами его деятельности. Познавательные процессы (восприятие, память, воображение, мышление) протекали в соответствии с этими программами, в результате чего сформировались и наследственные программы восприятия и усвоения знаний. Таким образом, если учебный материал излагать в той же последовательности, в какой обычно происходит изготовление материальных предметов, вероятно, он будет легче восприниматься, усваиваться и прочнее закрепляться в памяти.

В процессе изучения темы «Перпендикулярность в пространстве» студенты имеют дело с прямыми, плоскостями, двугранными углами, поэтому в практической деятельности они должны работать с предметами, напоминающими эти геометрические фигуры. В качестве домашнего задания можно предложить изготовить наглядные пособия, необходимые для объяснения темы, например, модели пересечения прямых и плоскостей, двух плоскостей, набор двугранных углов и т.д. Материалом могут служить рейки, куски проволоки, фанеры, картона, оргстекла, текстолита, пенопласта. Изготовливая макеты студенты могут выполнить дополнительные задания проблемного характера:

• просверлить ряд отверстий в толстостенной плите из оргстекла, дерева, текстолита или пенопласта, строго перпендикулярно плоскости ее основания, с помощью ручной дрели (плиту лучше прикрепить к стене);
  
• закрепить несколько деревянных реек перпендикулярно листу фанеры, металлических прутьев перпендикулярно листу фанеры или листу жести;
  
• закрепить два листа фанеры или картона, имеющих неправильную форму, под различными заданными углами (30⁰;90⁰;120⁰ и т.д.);
  
• прикрепить перпендикулярно листу фанеры или картона другой лист.
  

Выполняя такого рода задания, студенты сталкиваются с некоторыми трудностями, которые могут быть успешно преодолены, если используются знания основных положений темы. Так, при сверлении отверстий в плите трудно будет удержать дрель (сверло) перпендикулярно основанию плиты. Потребуются дополнительные приспособления, основанные на признаке перпендикулярности прямой и плоскости. Затруднения могут возникнуть при скреплении двух листов фанеры неправильной формы под заданным углом. Для успешного выполнения этого задания необходимо знать, как измеряются двугранные углы, что является их мерилом.

Параллельно с выполнением практических заданий перед изучением темы нужно повторить пройденный материал, который потребуется для раскрытия основных положений темы, а именно, признаки равенства треугольников, определение наклонной и перпендикулярной прямой (плоскости), понятие развернутого угла и т.д. После этого студенты в какой-то степени будут психологически готовы к восприятию материала темы, можно будет перейти к непосредственному ее изложению.

Первое занятие можно посвятить объяснению признаков перпендикулярности прямой и плоскости, двух плоскостей, понятий двугранного угла. Например, просверлить отверстие в плите перпендикулярно ее основаниям можно с помощью установки корпуса дрели между двумя прямоугольными треугольниками. Аналогичным приемом можно закрепить деревянные рейки перпендикулярно листу фанеры. В качестве дополнительного задания можно предложить ответить на вопросы о том, какие приспособления помогут строителям при забивке свай перпендикулярно плоскости земли, при установке оконных блоков и дверных коробок в проёмы, закреплении стропил крыши под заданным углом? На втором занятии можно рассмотреть решение задач прикладного характера, после чего вновь вернуться к изложению материала темы.

Анализ результатов контроля остаточных знаний по данной теме в группах показал, что там, где выполнялись практические задания дома, студенты проявляют больше самостоятельности, вычерчивая развертки геометрических тел, вычисляя их боковые и полные поверхности. Таким образом, описанная методика преподавания математики позволяет реализовать требования образовательных стандартов третьего поколения.