Тема: Построение
| Вид материала | Документы |
СодержаниеТаблица построения графиков функций, содержащих модуль. |
- Лекция Тема «Построение эффективной системы взаимоотношений оптовой и розничной торговли», 111.43kb.
- Рецензи я, 16.05kb.
- Тема: «Шаги различных видов», 590.24kb.
- Контрольная работа по теории физической культуры тема, 434.78kb.
- Шейчекова Марина Евгеньевна, 10А класс Научный Кулигина Анна Леонидовна, учитель информатики, 18.75kb.
- Урок технологии в 7 классе Тема: Построение чертежа ночной сорочки, 65.27kb.
- Тема: «Построение индивидуальной траектории развития образования и воспитания», 43.93kb.
- Урок литературы в 7 классе. Тема: «каким должен быть человек на войне?», 36.65kb.
- Название темы, 116.47kb.
- Тема : Метрика, 371.35kb.
9 КЛАССЫ
Тема: Построение графиков функции, содержащих модуль.
- Пример 1. Построить график функции у = х2 - 6х + 3. Найти нули функции.
Решение.
1. Направление “ветвей” параболы: если а = 1, а > 0, то “ветви” параболы направлены вверх.
2. Координаты вершины параболы: х= - b/2а = - (-6)/2=3, у(3) = 9 – 18 + 3 = - 6, А(3; -6).
3. Уравнение оси симметрии: х = 3.
4. Нули функции: у(х) = 0, х2 - 6х + 3 = 0, D = 36 - 4·3 = 36 – 12 = 24, D>0,
x 1,2 = (6 ±
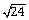 )/2 = 3 ±
)/2 = 3 ± 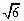 ; В(3 -
; В(3 - 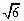 ;0), С(3 +
;0), С(3 + 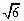 ;0).
;0).График на рис.1.
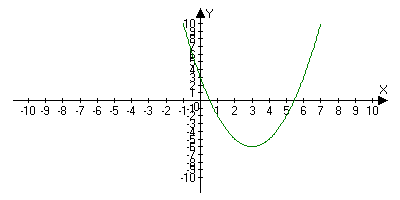
Рис.1.
Алгоритм построения графика квадратной функции.
1. Определить направление “ветвей” параболы.
2. Вычислить координаты вершины параболы.
3. Записать уравнение оси симметрии.
4. Вычислить несколько точек.
б) Рассмотрим построение графиков линейных функций, содержащих модуль:
1. у = |х|. График функции на рисунке 2.
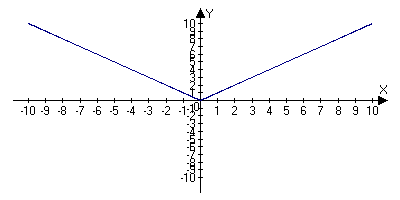
Рис. 2.
2. у = |х| + 1. График функции на рисунке 3.
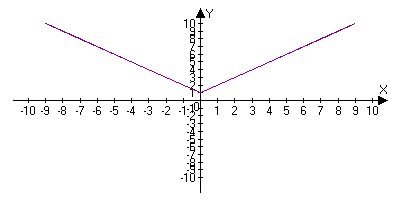
Рис.3.
3. у = |х + 1|.
1. График функции у = |х| + 1 получается из графика функции у = |х| параллельным переносом на вектор {0;1}.
2. График функции у = |х + 1| получается из графика функции у = |х| параллельным переносом на вектор {-1;0}.
- Операционно-исполнительная часть.
Этап исследовательской работы. Работа в группах.
Группа 1. Построить графики функций:
а) у = х2 - 6|x| + 3,
б) у = |х2 - 6х + 3|.
Решение.
а)
1. Построить график функции у = х2-6х+3.
2. Отобразить его симметрично относительно оси Оу.
График на рисунке 5.

Рис.5.
б) 1. Построить график функции у = х2 - 6х + 3.
2. Отобразить его симметрично относительно оси Ох.
График функции на рисунке 6.
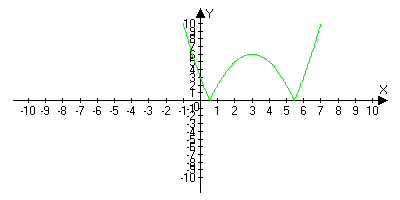
Рис. 6.
Вывод.
1. График функции у = f(|x|) получается из графика функции у = f(x), отображением относительно оси Оу.
2. График функции у = |f(x)| получается из графика функции у = f(x), отображением относительно оси Ох.
Группа 2. Построить графики функций:
а) у = |x2 - 6|x| + 3|;
б) y = |x2 - 6x + 3| - 3.
Решение.
а)
1. График функции у = х2 + 6x + 3 отображаем относительно оси Оу, получается график функции у = х2 - 6|x| + 3.
2. Полученный график отображаем симметрично относительно оси Ох.
График функции на рисунке 7.
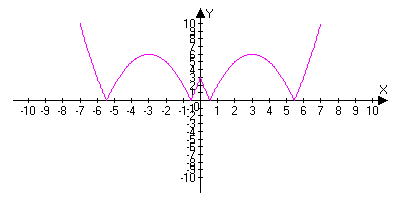
Рис.7.
Вывод.
График функции y = |f (|x|)| получается из графика функции у = f(х), последовательным отображением относительно осей координат.
б)
1. График функции у = х2 - 6х + 3 отображаем относительно оси Ох.
2. Полученный график переносим на вектор {0;-3}.
График функции на рисунке 8.
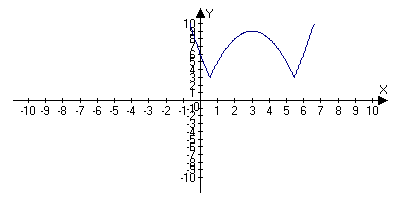
Рис.8.
Вывод. График функции у = |f(x)| + a получается из графика функции у = |f(x)| параллельным переносом на вектор {0,a}.
Группа 3.Построить график функции:
а) у = |x|(х - 6) + 3; б) у = х|x - 6| + 3.
Решение.
а) у = |x| (x - 6) + 3, имеем совокупность систем:
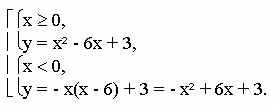
Строим график функции у = -х2 + 6x + 3 при х < 0 для точек у(0) = 3, у( - 1) = - 4.
График функции на рисунке 9.
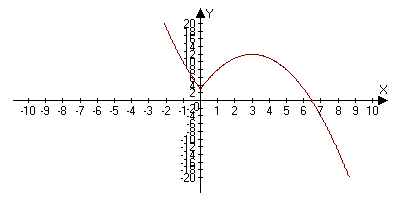
Рис.9.
б) у = х |х - 6| + 3, имеем совокупность систем:
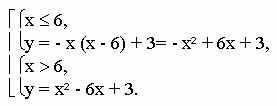
Строим график функции у = - х2 + 6х + 3 при х
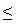 6.
6.1. Направление “ветвей” параболы: а = - 1, а < 0, “ветви” параболы направлены вниз.
2. Координаты вершины параболы: х = - b/2a = 3, у(3) =1 2, А(3;12).
3. Уравнение оси симметрии: х = 3.
4. Несколько точек: у(2) = 11, у(1) = 3; у(-1) = - 4.
Строим график функции у = х2 - 6х + 3 при х = 7 у(7) = 10.
График на рис.10.
Рис.10.
Вывод. При решении данной группы уравнений необходимо рассматривать нули модулей, содержащихся в каждом из уравнений. Затем строить график функции на каждом из полученных промежутков.
(При построении графиков данных функций каждая группа исследовала влияние модуля на вид графика функции и сделала соответствующие заключения.)
Получили сводную таблицу для графиков функций, содержащих модуль.
Таблица построения графиков функций, содержащих модуль.
| Вид функции | Способ построения графика функции |
| 1. у = f(|x|) 2. у = |f(x)| 3. у = |f(|x|)| 4. у = |f(x)| + a | 1. Отобразить график функции у = f(x) симметрично относительно оси Оу. 2. Отобразить график функции у = f(x) симметрично относительно оси Ох. 3. Последовательно отобразить график функции у = f(x) симметрично относительно осей координат. 4. Параллельный перенос перенос графика функции у = |f(x)|на вектор {0;а}. |
Группа 4.
Построить график функции:
а) у = х2 - 5x + |x - 3|;
б) у = |x2 - 5x| + x - 3.
Решение.
а) у = х2 - 5х + |х - 3|, переходим к совокупности систем:
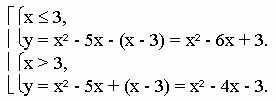
Строим график функции у = х2 -6х + 3 при х
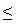 3,
3, затем график функции у = х2 - 4х - 3 при х > 3 по точкам у(4) = -3, у(5) = 2, у(6) = 9.
График функции на рисунке 11.
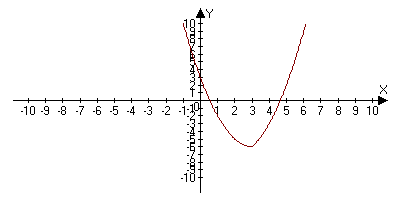
Рис.11.
б) у = |х2 - 5х| + х - 3, переходим к совокупности систем:
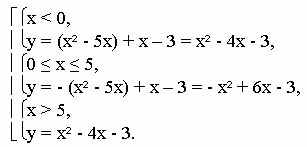
Строим каждый график на соответствующем интервале.
График функции на рисунке 12.
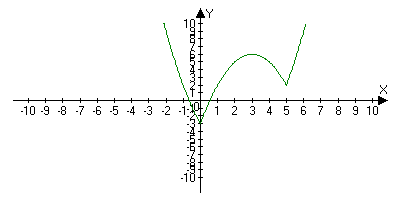
Рис.12.
Вывод.
Выяснили влияние модуля в каждом слагаемом на вид графика.
- Самостоятельная работа.
Построить график функции:
а) у = |х2 - 5х + |x - 3||,
б) у= ||x2 - 5x| + х - 3|.
Решение.
Предыдущие графики отображаем относительно оси Ох.
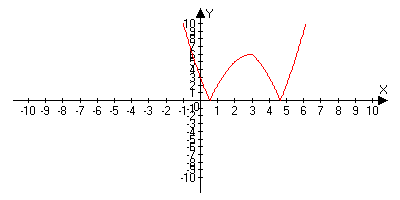
Рис.13.
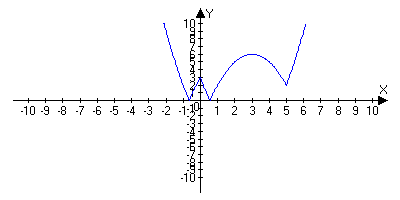
Рис. 14.
Группа.5
Построить график функции: у =| х - 2| (|x| - 3) - 3.
Решение.
Рассмотрим нули двух модулей: x = 0, х – 2 = 0. Получим интервалы постоянного знака.
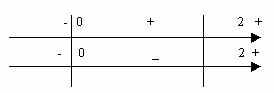
Имеем совокупность систем уравнений:
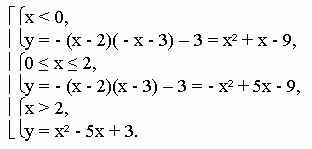
Строим график на каждом из интервалов.
График на рисунке 15.
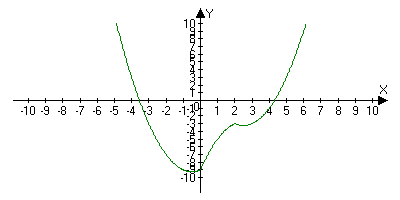
Рис.15.
- Задание на дом.
Построить графики функций с различным расположением модуля:
1. у = х2 + 4х + 2;
2. у = - х2 + 6х - 4.
