Geum.ru

«геометрические построения»

Вид материалаРешение

Содержание


История циркуля
Окружность вокруг нас
Построение касательной к окружности.
Построение отрезка, четвёртого пропорционального к трём данным отрезкам.
Разделение дуги
Подобный материал:
Муниципальное общеобразовательное учреждение

Средняя общеобразовательная школа № 17 г. Пензы


РЕФЕРАТ

На тему:

«ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ»


Выполнил: ученик 8 Б класса

Хохлов Игорь Вадимович

Руководитель: Дорофеева

Людмила Геннадьевна


г. Пенза, 2011г.

СОДЕРЖАНИЕ


Стр.


Введение 3

История циркуля 3

Окружность вокруг нас 6

Построение касательной к окружности 9

Решение задач 12

Заключение 14

Список литературы 16


ВВЕДЕНИЕ

Цель реферата: на примере ряда задач показать, что при решении задач на построение можно обходиться только одним инструментом, познакомиться с историей создания циркуля.

Задачи реферата: изучить научно – историческую  литературу по теме; подбор соответствующих теме реферата задач и их доказательство; показать красоту и занимательность задач на  построение. Ознакомиться с конструированием на компьютере и изучить редакторы, применяющиеся для этого, создать презентацию.

В школе мы выполняем геометрические построения с помощью окружностей, изучаем касательные к окружности, но не строим их. Я хотел бы узнать, всегда ли можно построить касательную к окружности и как это сделать. Геометрические построения - это способ решения задачи, при котором ответ получают графическим путем. Построения выполняют чертежными инструментами при максимальной точности и аккуратности работы, так как от этого зависит правильность решения. А когда появились первые циркули? И кто придумал этот замечательный инструмент? Раздел геометрии, в котором изучаются геометрические построения, называется конструктивной геометрией. Основным понятием конструктивной геометрии является понятие построить геометрическую фигуру. Это понятие принимается без определения, конкретный его смысл известен из практики, где оно означает: начертить, провести (линию), отметить (точку). В интересах логической строгости изложения основное понятие конструктивной геометрии - построить фигуру - характеризуется через основные требования (общие аксиомы конструктивной геометрии).


ИСТОРИЯ ЦИРКУЛЯ


Циркуль знаком каждому человеку со школы - на уроках черчения нельзя обойтись без этого инструмента для рисования окружностей и дуг. Кроме того, его используют для измерения расстояний, например, на картах, его применяют в геометрии и для навигации. Обычно циркуль делается из металла и состоит из двух «ножек», на конце одной из них находится игла, на второй пишущий предмет, обычно графитный грифель. В случае если циркуль измерительный, на обоих его концах расположены иглы. Само слово циркуль происходит от латинского circulus - «круг, окружность, кружок», от латинского же circus - «круг, обруч, кольцо». В русский язык циркуль или циркул пришел от польского cyrkuɫ или немецкого Zirkel.



Сейчас уже нельзя сказать, кто именно изобрел этот инструмент - история не сохранила для нас его имя, но легенды Древней Греции приписывают авторство Талосу, племяннику знаменитого Дедала, первого «воздухоплавателя» древности.



История циркуля насчитывает уже несколько тысяч лет - судя по сохранившимся начерченным кругам, инструмент был знаком еще вавилонянам и ассирийцам (II - I века до нашей эры). На территории Франции, в галльском кургане был найден железный циркуль (I век нашей эры), во время раскопок в Помпеях было найдено много древнеримских бронзовых циркулей. Причем в Помпеях найдены инструменты уже совсем современные: циркули с загнутыми концами для измерения внутренних диаметров предметов, «кронциркули» для измерения максимального диаметра, пропорциональные - для кратного увеличения и уменьшения размеров. При раскопках в Новгороде был найден стальной циркуль-резец для нанесения орнамента из мелких правильных кружочков, очень распространенного в Древней Руси. Со временем конструкция циркуля практически не изменилась, но ему придумали массу насадок, так что теперь он может вычерчивать окружности от 2 миллиметров до 60 сантиметров, кроме того, обычный графитный грифель можно заменить насадкой с рейсфедером для черчения тушью. Есть несколько основных типов циркулей: разметочный или делительный. Его применяют для снятия и перенесения линейных размеров; чертежный или круговой, его применяют для вычерчивания окружностей диаметром до 300 миллиметров; чертежный кронциркуль для вычерчивания окружностей от 2 до 80 миллиметров в диаметре; чертежный штангенциркуль для вычерчивания окружностей диаметром больше 300 миллиметров; пропорциональный - для изменения масштабов снимаемого размера. Циркуль используется не только в черчении, навигации или картографии - применение ему нашлось и в медицине: например, большой и малый толстотные циркули применяются для измерения поперечных размеров тела человека и для измерения размеров черепа соответственно, а циркуль - калипер используется для измерения толщины подкожно-жировой складки. Также известен циркуль Вебера, немецкого психофизиолога и анатома, разработанный им для определения порога кожной чувствительности. Но циркуль - не только всем известный инструмент. Этим словом названо маленькое созвездие южного полушария к западу от «Наугольника» и «Южного треугольника», рядом с α - Центавра. К сожалению, на территории России это созвездие не наблюдается. Кроме того, циркуль является символом неуклонной и беспристрастной справедливости, совершенной фигурой круга с центральной точкой, источником жизни. Наряду с квадратом циркуль определяет пределы и границы прямой линии. В ритуальной архитектуре циркуль символизирует трансцендентное знание, архетип, контролирующий все работы, навигатора. У китайцев циркуль означает правильное поведение. Циркуль - атрибут Фо-хи, легендарного китайского императора, считавшегося бессмертным. Сестра Фо-хи имеет квадрат, и вместе они - мужской и женский принципы, гармония инь и янь. У греков циркуль наряду с глобусом являлся символом Урании, покровительницы астрономии. Циркуль, совмещенный с наугольником - одна из самых распространенных эмблем, символов и знаков масонов. На этой эмблеме циркуль символизирует Небесный Свод, а наугольник - землю. Небо в данном случае символически связано с местом, где чертит план Великий Строитель Вселенной. Буква «G» в центре в одном из значений - сокращение слова «геометр», используемого в качестве одного из названий верховного существа.


ОКРУЖНОСТЬ ВОКРУГ НАС


Окружность - это линия, состоящая из всех точек плоскости, которые находятся на заданном расстоянии от одной точки плоскости, называемой центром окружности.

Окружность – удивительно гармоничная фигура, древние греки считали её самой совершенной. Совершенство окружности – в расположении всех её точек на одинаковом расстоянии от центра. Именно поэтому окружность – единственная кривая, которая может “скользить сама по себе ”, вращаясь вокруг центра.

Окружность как совершенная геометрическая форма всегда привлекала к себе внимание художников, архитекторов. В неповторимом архитектурном облике Санкт-Петербурга восторг и удивление вызывает “чугунное кружево” – садовые ограды, перила мостов и набережных, балконные решётки, фонари. Чётко просматриваемое на фоне фасадов зданий летом, в изморози зимой, оно придаёт особое очарование городу. На рисунке 1 изображены ворота Таврического дворца, созданного в конце 18 века архитектором Ф.И.Волковым. Особую воздушность придают воротам окружности, сплетённые в орнамент.

Рис.1. Ворота Таврического дворца. С.-Петербург

Торжественность и устремлённость ввысь – такой эффект в архитектуре зданий достигается использованием арок, представляющих дуги окружностей (рис. 2).

рис.2. К. Росси. Арка Главного штаба. С.-Петербург

Окружности и дуги являются основными элементами готических храмов средневековья (рис.3.)



Рис.3. Витраж собора св. Витта. Прага.

Основное свойство окружности даёт ответ на вопросы, почему для её вычерчивания используют циркуль и почему колёса делают круглыми, а не квадратными или, например, треугольными. Кстати, о колесе. Это одно из самых великих изобретений человечества. Оказывается, додуматься до колеса было не так просто, как это может показаться. Ведь даже ацтеки, жившие в Мексике, почти до 16 веке не знали колеса.

Окружность обладает ещё одним интересным свойством. Возьмём верёвочку и свяжем её в кольцо, положив полученное кольцо на плоскость, сделаем из него разные фигуры: квадрат, треугольник, окружность и т.д.

Площадь, ограниченная окружностью (т. е. площадь круга), - наибольшая среди поученных таким образом площадей.


ПОСТРОЕНИЕ КАСАТЕЛЬНОЙ К ОКРУЖНОСТИ.


К числу конструктивных задач в курсе школьной планиметрии относится построение циркулем и линейкой касательной к окружности.

Возможны три случая:
а) точка А лежит на окружности;
б) точка С лежит вне круга;
в) точка В лежит в круге.


Случай а) Задача имеет единственное решение.

Построение касательной к окружности w (O,R) в точке A принадлежащей окружности.

Касательная к точке, лежащей на окружности (рис. 1, а). Касательная к окружности должна быть перпендикулярна радиусу, проведенному через точку касания. Поэтому проводят радиус ОА и в точке А строят перпендикуляр к ОА. Прямая ВС — искомая касательная. На рисунке показано построение касательной к окружности с помощью чертежной линейки и угольника.



Касательная к окружности может быть построена и другим способом (рис.1,6). Через центр окружности О и заданную точку А проводят прямую и на ее продолжении откладывают отрезок АВ, равный радиусу. Через точку. А строят прямую DC, перпендикулярную прямой ОВ, она и будет касательной к окружности в точке А.

Случай б)
Более содержательной и поучительной задачей является построение к окружности w (А,R) касательной, проходящей через точку С, не принадлежащую ей.
Задача имеет два решения.

Способ1
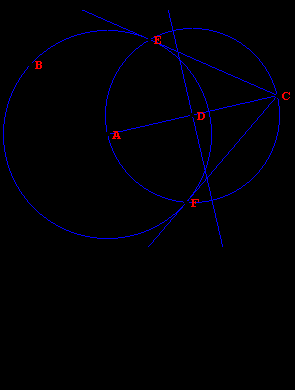
  1. Строим серединный перпендикуляр к отрезку АС.
  2. Находим середину отрезка АС (точка D).
  3. Строим окружность с центром в точке D и радиусом AD.
  4. Находим точки пересечения окружностей E и F.
  5. Строим прямые CF и EF. Это искомые касательные.





Способ 2

Касательную из точки А к окружности можно провести следующим образом:

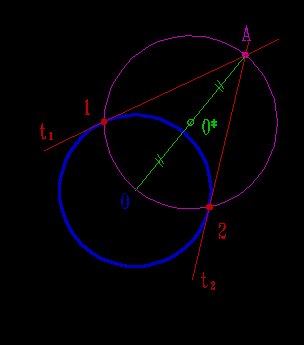
1. На отрезке ОА как на диаметре строят окружность радиуса R=0,5[OA];

2. Точки 1 и 2 пересечения полученной окружности с заданной определяют положение точек касания;

3. Отрезки [1A] и [2A] определяют положение касательных t1 и t2 проведенных из точки А к окружности.




Случай в). Задача не имеет решений.


Задача 1. ПОСТРОЕНИЕ ОТРЕЗКА, ЧЕТВЁРТОГО ПРОПОРЦИОНАЛЬНОГО К ТРЁМ ДАННЫМ ОТРЕЗКАМ.

Дано: а, б, с – отрезки.

Построить: отрезок х такой, чтобы а:б=с:х.

Построение: Берём произвольную точку О и проводим окружности (О; а) и (О; б). Из произвольной точи А на окружности (О; а) описываем (А; с) и отмечаем точку В пересечения её с окружностью (О; а). Если теперь две окружности (А; d) и (В; d) произвольного радиуса d>| а –б |, пересекающие (О; б) в точках А1 и В1, то отрезок х=| А1 В1| - искомый.



Доказательство: треугольник АОА1 подобен треугольнику ВОВ1 (по трём сторонам), поэтому АОА1= ВОВ1 и АОВ=А1 ОВ1. Равнобедренные треугольники АОВ и А1 ОВ1 подобны следовательно,

а : б = с : |А1В1|.

Приведённое построение возможно, при с<2а. При c>=2а и б<2а строим отрезок, четвёртый пропорциональный к отрезкам а, с и б; в противном случае (с>=2а и б>=2а) сначала строим отрезок na, при этом n берём таким, чтобы c<2па* (или б < 2па). Строим отрезок у, четвёртый пропорциональный к отрезкам па, б и с. Если теперь построить отрезок х = п у, то получим четвёртый пропорциональный отрезкам а, б и с.


Задача 2. РАЗДЕЛЕНИЕ ДУГИ АВ ОКРУЖНОСТИ (О,r) ПОПОЛАМ.

Можно предположить, что центр О окружности известен.

Построение: Пологая а =|АВ|, проводим окружности (O ,a), (А,r) и (В,r); в пересечении получим точки С и D. В пересечении окружностей (С,|СВ|) и (D,|AD|) получим точку Е. Если теперь начертить окружности (С, |ОЕ|), то в пересечении их получим точки Х и Х1. Точка Х делит пополам дугу АВ , точка Х1 делит пополам дугу , дополняющую первую до полной окружности. (В том случае, когда окружность(О,r) начерчена, из двух окружностей (С, |ОЕ|) и(D,|ОЕ|) можно описывать только одну, которая а пересечении с окружностью (О,r) определит точки Х и Х1 ). В геометрии циркуля прямую линию принято считать построенной, как только определены две её точки.



ЗАКЛЮЧЕНИЕ

Благодаря этой работе я познакомился с историей возникновения циркуля, посмотрел на окружающие меня предметы с позиции геометрии, стал лучше ориентироваться в черчении, ознакомился с правилами выполнения творческой работы, получил новые знания и применил их на практике.

Решение задач на построение циркулем и линейкой – полезное времяпровождение, позволяющее по-новому посмотреть на известные свойства геометрических фигур и их элементов.

Мне бы хотелось как можно больше использовать свои новые полученные знания на практике.

В настоящем реферате рассмотрены наиболее актуальные задачи, связанные с геометрическими построениями.. Рассмотрены различные задачи и даны их решения. Приведенные задачи имеют значительный практический интерес, закрепляют полученные знания по геометрии и могут использоваться для практических работ. Ценно то, что для их решения не требуется знаний больших, чем в объеме 8 классов.

Кроме того, при работе над рефератом мною освоен текстовый редактор Word, графический редактор PhotoShop, редактор Web- страниц FrontPage.

Таким образом, цель реферата достигнута, задачи реферата выполнены.


СПИСОК ЛИТЕРАТУРЫ


  1. Наглядная геометрия 5-6 класс Шарыгин И.Ф. Ерганжиева Л. Н.
  2. Истории обыкновенных вещей В.В. Богданов, С.Н. Попов
  3. Геометрические миниатюры З.А. Скопец
  4. Геометрические построения одним циркулем А.Н.Костовский
  5. ссылка скрыта