Geum.ru

Учебно-методический комплекс учебной дисциплины Геометрические построения Специальность 032200. 00 Физика

Вид материалаУчебно-методический комплекс

Содержание


Форма обучения дневная
Рабочая программа
Форма обучения дневная
1.2 Цели и задачи дисциплины.
2. Структура учебной дисциплины.
3. Содержание учебной дисциплины
3.2 Содержание практических занятий
4. Методические материалы и рекомендации для преподавателя
4.2. Варианты индивидуальных работ по школьным учебникам
4.3. Варианты контрольной работы по курсу
5. Методические рекомендации студентам
6. Формы текущего, промежуточного и итогового контроля.
Промежуточный контроль
Подобный материал:
Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Псковский государственный педагогический университет

имени С.М. Кирова


Физико-математический факультет

Кафедра алгебры и геометрии


УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС

учебной дисциплины

Геометрические построения


Специальность 032200.00 Физика

с дополнительной специальностью математика


Физико-математический факультет

Форма обучения дневная

4 курс 7 семестр


Псков 2007

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Псковский государственный педагогический университет

имени С.М. Кирова

Физико-математический факультет

Кафедра алгебры и геометрии

«Утверждаю»

Декан физико-математического факультета

_______________И.Н. Медведева

«_____»_____________200__г.


РАБОЧАЯ ПРОГРАММА

учебной дисциплины

ДДС.04. Геометрия (геометрические построения)


Специальность 032200.00 Физика

с дополнительной специальностью математика

Физико-математический факультет

Форма обучения дневная

4 курс: 7 семестр


Всего часов: 72

Лекции: 10

Практические работы: 26

Самостоятельная работа: 36

Зачет: 7 семестр


Псков

2007

Рабочая программа составлена на основании Государственного образовательного стандарта высшего профессионального образования по специальности 032200.00 физика с дополнительной специальностью математика.


Номер государственной регистрации

№ 694 пед/сп (новый)

«31» января 2005 г.


ДДС.04. Геометрия (геометрические построения)


Рабочая программа принята на заседании кафедры алгебры и геометрии.


Протокол № ____ заседания кафедры

«____»____________ 200 __ г.


Программа разработана ассистентом кафедры алгебры и геометрии


__________________________ Д.С. Лобарёв


Заведующий кафедрой алгебры и геометрии

________________________ И.Н. Медведева


1. Пояснительная записка

1.1 Требования к содержанию учебной дисциплины из Государственного образовательного стандарта.


1.2 Цели и задачи дисциплины.

Курс геометрических построений на плоскости в педагогическом институте имеет своей целью познакомить студентов с основами конструктивной геометрии, с типами задач на построения, методиками решения задач на построения с помощью циркуля и линейки:
  • метод ГМТ
  • метод подобия
  • метод движения
  • метод инверсии
  • алгебраический метод

, с классическими задачами неразрешимыми с помощью циркуля и линейки:
  • задача об удвоении куба
  • задача о трисекции угла
  • задача о квадратуре круга

Курс геометрических построений имеет разнообразные межпредметные связи с школьными и институтскими курсами «Геометрия», «Алгебра», «Математический анализ». А поэтому данный раздел геометрии способствует целостному формированию естественно-научного знания студентов о мире, что в свою очередь способствует творческому развитию личности средствами представления изображений при осуществлении анализа и решения геометрических задач на построение циркулем и линейкой.

В результате изучения курса студенты должны овладеть методиками решения задач на построения с помощью циркуля и линейкой, должны уметь решать все задачи на построения школьного курса геометрии, иметь представления о задачах, неразрешимых циркулем и линейкой, и овладеть иными методами их разрешения.


2. Структура учебной дисциплины.

№ п/п

Тема
ЛК (час.)
ПЗ (час.)
СР (час.)
Всего (час.)

1
Введение
1
-
1
2

2
Основание конструктивной геометрии
1
-
1
2

3
Взаимное расположение двух окружностей
1
-
1
2

4
Основные построения
1
4
5
10

5
Решение задач на построение методом ГМТ
1
6
7
14

6
Применение движения к решению задач на построение
1
2
3
6

7
Метод подобия
1
4
5
10

8
Алгебраический метод
1
4
5
10

9
Инверсия. Метод инверсии
1
4
5
10

10
Классические задачи, неразрешимые циркулем и линейкой
1
2
3
6




ИТОГО
10
26
36
72



3. Содержание учебной дисциплины

3.1 Содержание лекционного курса

№ лек.
Тема лекции
Содержание лекции
Вид контроля

1
Введение
Из истории возникновения. Связь с другими дисциплинами. Основания конструктивной геометрии. Аксиомы. Простейшие построения.



2
Основные построения
Взаимное расположение двух прямых, взаимное расположение прямой и окружности, двух окружностей.

Построение отрезка, угла, треугольника, биссектрисы угла, перпендикулярной и параллельной прямой, прямоугольного треугольника и касательной к окружности.

Самостоятельная работа

3
Метод ГМТ

Метод движения
Определение ГМТ. Задачи ШКМ. Окружность, дуги окружностей, прямые отстоящие на данном расстоянии, окружность Апполония. Определение движения. Виды движений: параллельный перенос, осевая симметрия, поворот. Метод движения при решении задач на построения
Коллоквиум

4
Метод подобия Метод инверсии
Определение подобия. Метод подобия при решении задач на построения. Примеры. Инверсия. Теоремы инверсии. Метод инверсии при решении задач на построения. Примеры.
Самостоятельная работа

5
Алгебраический метод
Алгебраический метод при решении задач на построения. Основные алгебраические построения: построение суммы, разности двух отрезков, их среднего геометрического, отрезка четвертого пропорционального трем и т.п. Классические задачи неразрешимые циркулем и линейкой: об удвоении куба, трисекция угла и квадратура круга.
Самостоятельная работа


3.2 Содержание практических занятий

№ занят.
Тема практического занятия
Содержание практического занятия
Вид контроля

1-2
Основные построения
Задачи на основные построения. Самостоятельная работа.
Самостоятельная работа

3-5
Метод ГМТ
Задачи на метод ГМТ. Построение треугольника по основанию высоте, противолежащему углу и высоте. Построение треугольника по основанию высоте, и сумме (разности) квадратов боковых сторон и т.п. Коллоквиум.
Коллоквиум

6-8
Метод движения и подобия
Задачи на метод движения и подобия. Построения треугольника по 3-м медианам. Вписать равносторонний треугольник в квадрат. Построение трапеции и т.п.
Самостоятельная работа

9-10
Алгебраический метод
Построение отрезков и углов по формулам. Задачи, решаемые алгебраическим методом. Построить квадрат равновеликий двум прямоугольникам и т.п. Самостоятельная работа
Самостоятельная работа

11-12
Метод инверсии
Построение образов точек при инверсии, образов прямых и окружностей.

Задачи на метод инверсии.
Самостоятельная работа

13
Задачи неразрешимые циркулем и линейкой
Классические задачи неразрешимые циркулем и линейкой: об удвоении куба, трисекция угла и квадратура круга.





4. Методические материалы и рекомендации для преподавателя

4.1. Примерный перечень контрольных вопросов и заданий

к коллоквиуму.
  1. Построить множество точек плоскости, каждая из которых равноудалена от двух данных точек A и B.
  2. Построить множество точек плоскости, находящихся на данном расстоянии от данной прямой.
  3. Построить множество точек плоскости, каждая из которых равноудалена от двух данных параллельных прямых.
  4. Построить множество точек плоскости, каждая из которых равноудалена от двух данных пересекающихся прямых.
  5. Построить множество точек плоскости, из которых отрезок AB виден под прямым углом.
  6. Построить множество точек плоскости, из которых отрезок AB виден под углом , где .
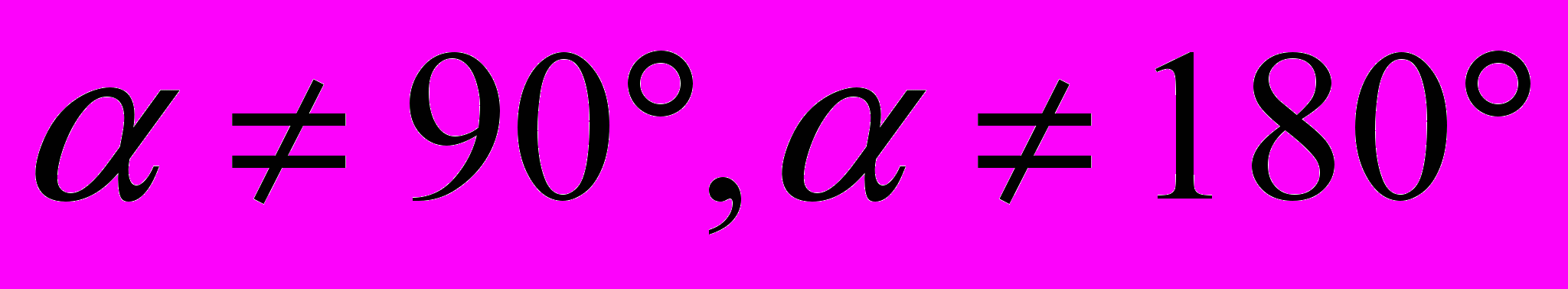  7. Построить множество точек плоскости, из которых данная окружность видна под углом , где .
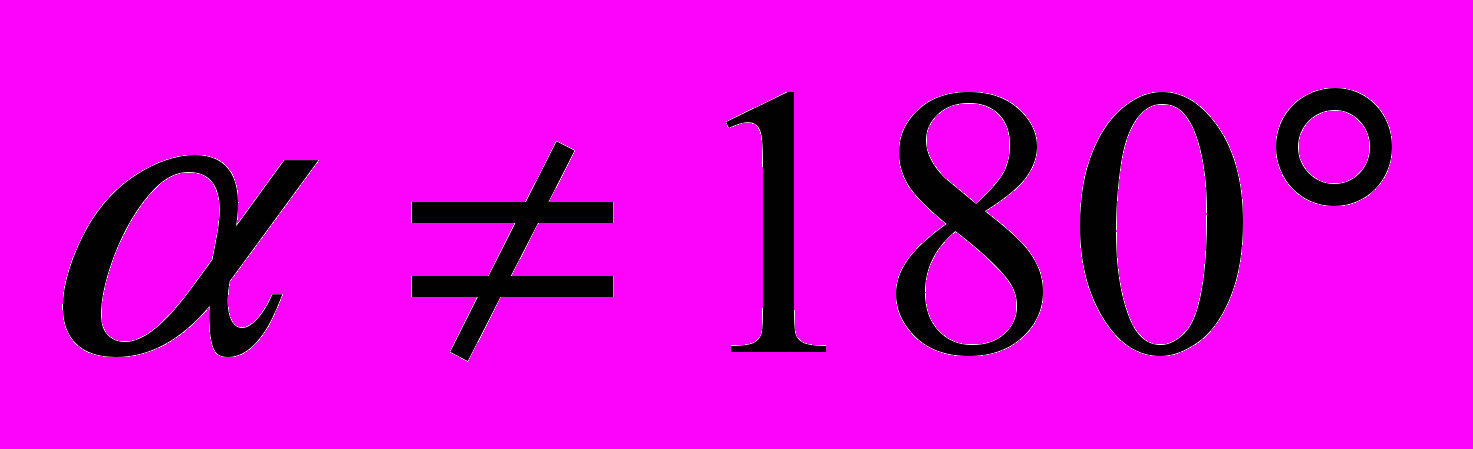  8. Построить множество точек плоскости, делящих всевозможные хорды окружности 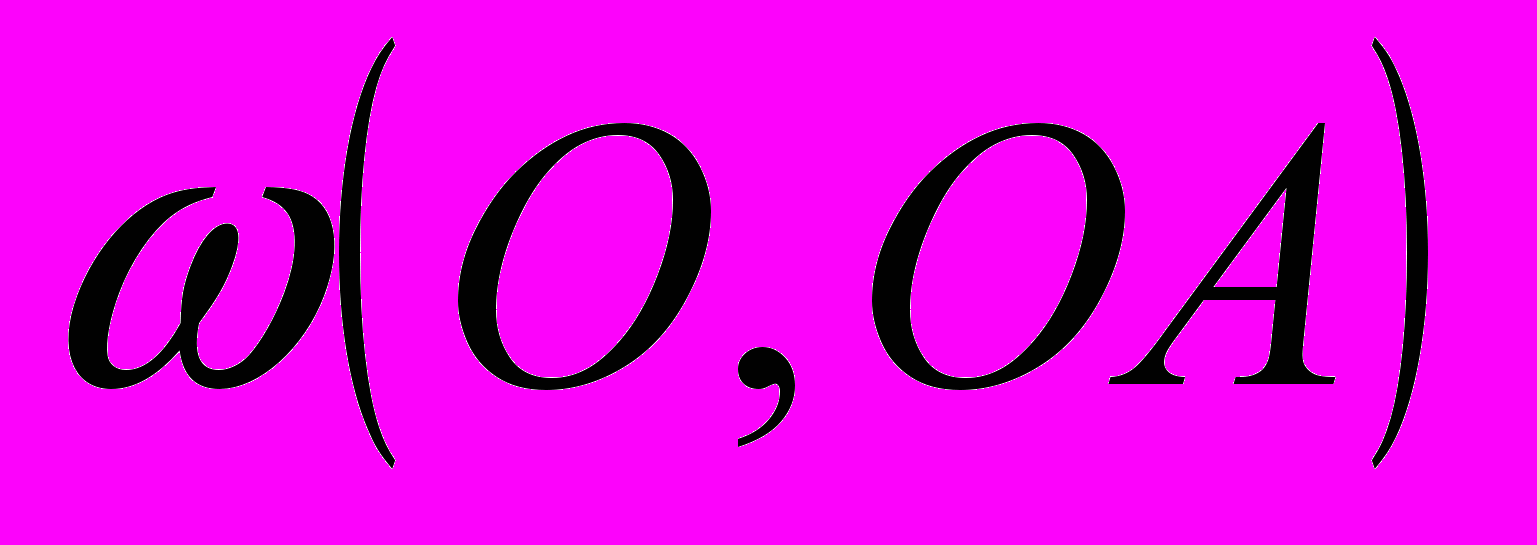, проведенные через точку A окружности, в одном и том же отношении .
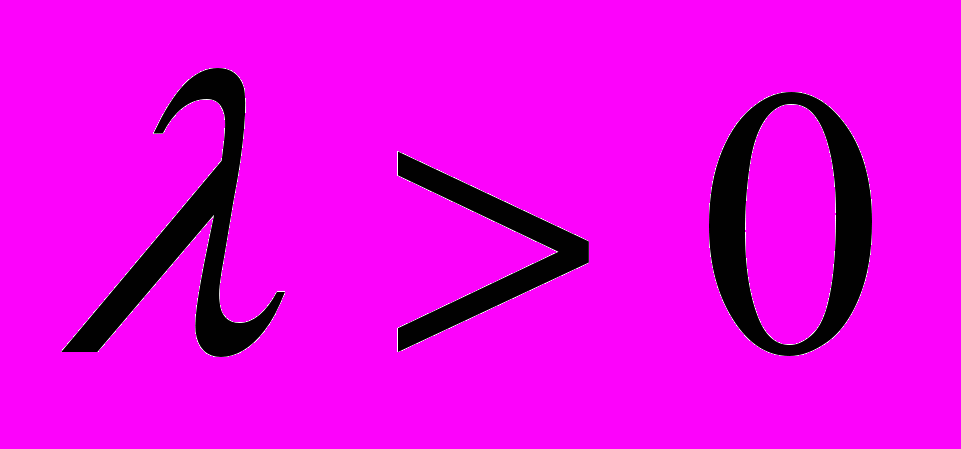  9. Построить множество точек плоскости, для каждой из которых разность квадратов расстояний от двух данных точек A и B постоянна.
  10. Построить множество точек плоскости, для каждой из которых сумма квадратов расстояний до двух данных точек A и B равна .
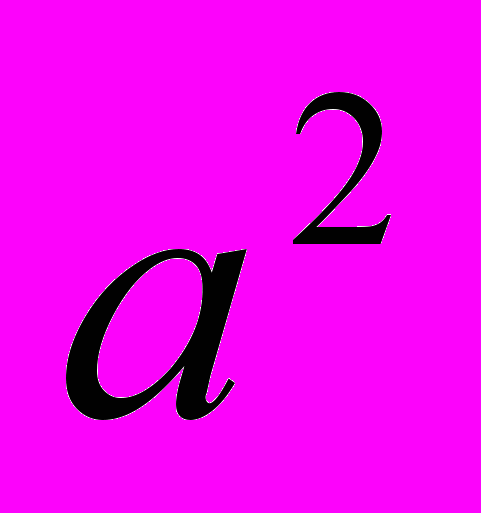  11. Построить множество точек плоскости, для каждой из которых отношение расстояний до двух данных точек A и B постоянно и отлично от единице.


4.2. Варианты индивидуальных работ по школьным учебникам

Вариант 1
  1. Погорелов. Геометрия 7-11, 78 стр., задача 19а.
  2. Погорелов. Геометрия 7-11, 80 стр., задача 44.
  3. Метод инверсии. Суть метода. Построения образа отрезка при инверсии.

Вариант 2
  1. Погорелов. Геометрия 7-11, 78 стр., задача 21.
  2. Погорелов. Геометрия 7-11, 80 стр., задача 45.
  3. Метод инверсии. Суть метода. Построения образа прямой, не проходящей через центр инверсии.

Вариант 3
  1. Погорелов. Геометрия 7-11, 78 стр., задача 22.
  2. Атанасян. Геометрия 7-9, задача 1231.
  3. Метод подобия (гомотетии). Построение окружности, гомотетичной данной.

Вариант 4
  1. Погорелов. Геометрия 7-11, 78 стр., задача 23 2-б.
  2. Погорелов. Геометрия 7-11, 79 стр., задача 40.
  3. Алгебраический метод. Суть метода. Построение отрезка .

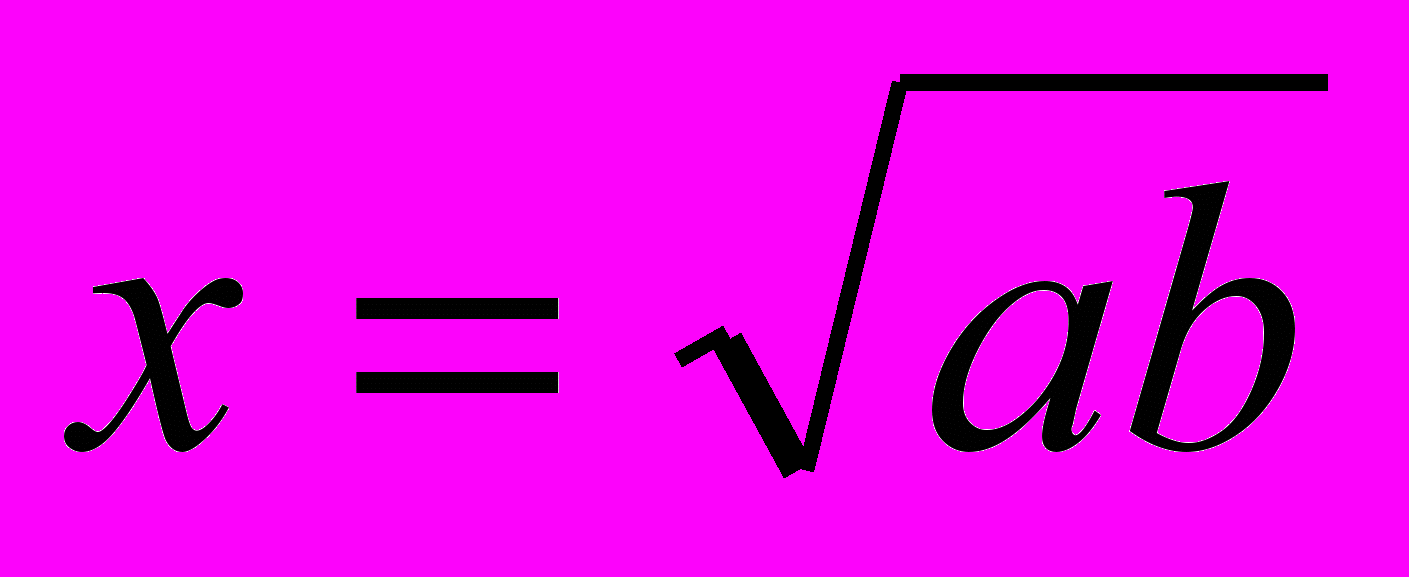Вариант 5
  1. Погорелов. Геометрия 7-11, 79 стр., задача 25.
  2. Погорелов. Геометрия 7-11, 80 стр., задача 46.
  3. Алгебраический метод. Суть метода. Построение отрезка .

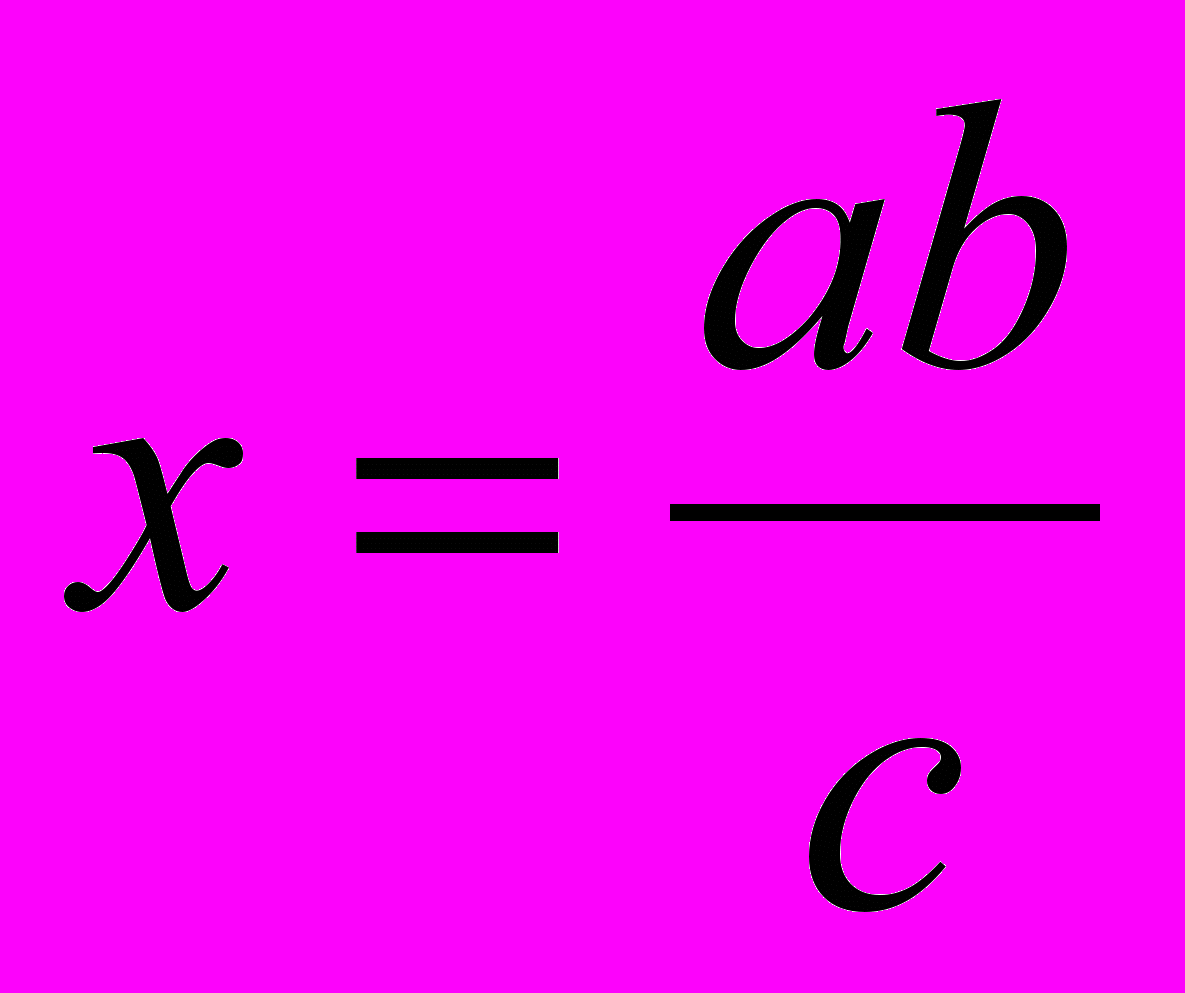Вариант 6
  1. Погорелов. Геометрия 7-11, 79 стр., задача 26.
  2. Погорелов. Геометрия 7-11, 80 стр., задача 47.
  3. Алгебраический метод. Суть метода. Построение корней квадратного уравнения (через дискриминант).

Вариант 7
  1. Погорелов. Геометрия 7-11, 79 стр., задача 27.
  2. Вернер. Геометрия 9, 142 стр., задача 7.
  3. Алгебраический метод. Суть метода. Построение корней квадратного уравнения по формулам Виета.

Вариант 8
  1. Погорелов. Геометрия 7-11, 79 стр., задача 28.
  2. Атанасян. Геометрия 7-9, 288 стр., задача 1228.
  3. Аксиомы и постулаты конструктивной геометрии.

Вариант 9
  1. Погорелов. Геометрия 7-11, 79 стр., задача 29.
  2. Атанасян. Геометрия 7-9, 212 стр., задача 871.
  3. Основные этапы решения задач на построение.

Вариант 10
  1. Погорелов. Геометрия 7-11, 79 стр., задача 30.
  2. Атанасян. Геометрия 7-9, 212 стр., задача 875.
  3. Метод ГМТ. Суть метода. Построение множества точек, для каждой из которых отрезок AB виден под углом , где , .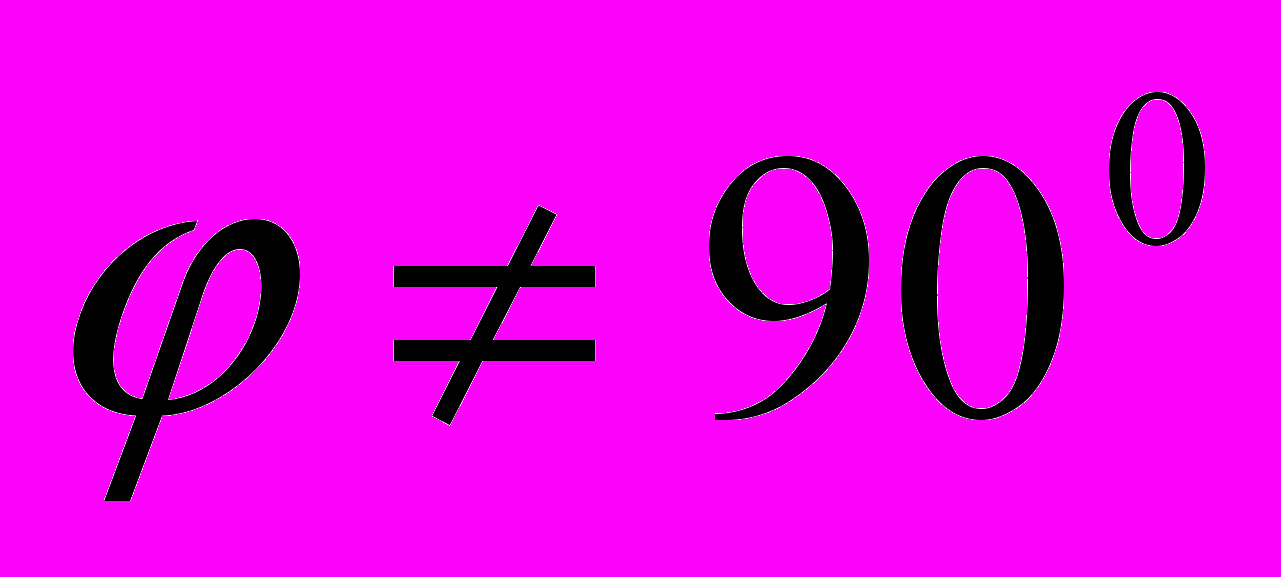


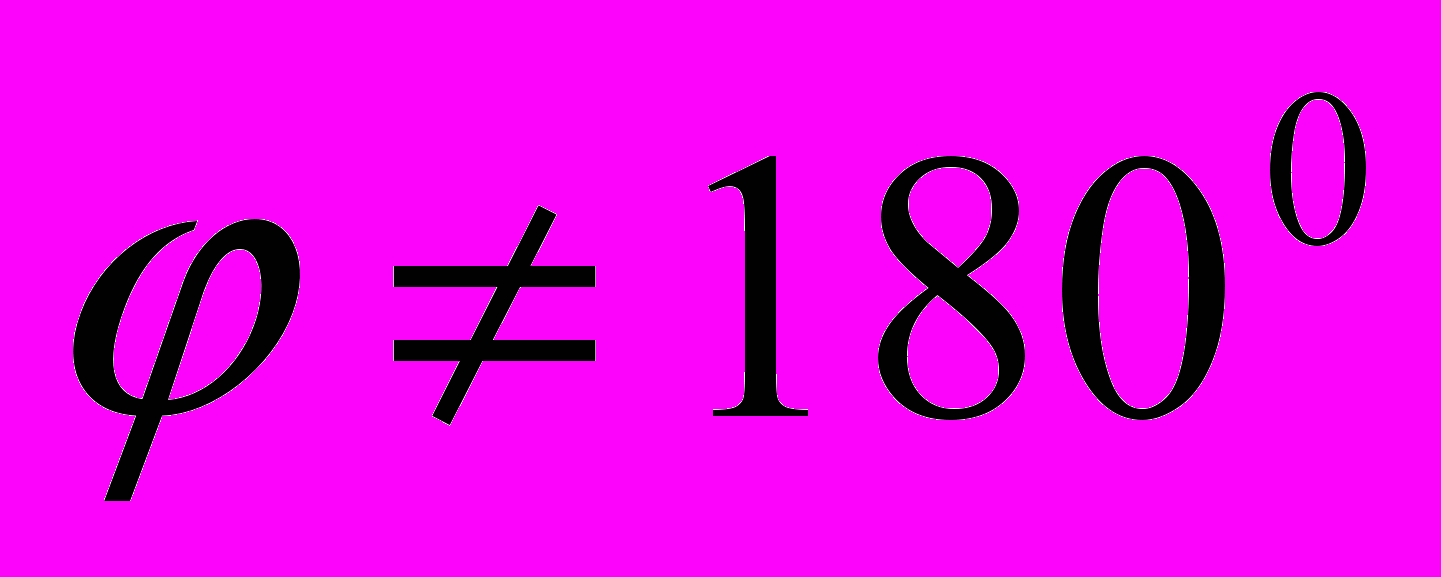Вариант 11
  1. Погорелов. Геометрия 7-11, 79 стр., задача 31.
  2. Вернер. Геометрия 9, 114 стр., задача 4.
  3. Метод ГМТ. Суть метода. Построение множества точек, для каждой из которых сумма квадратов расстояний до двух данных точек A и B постоянно и равно .

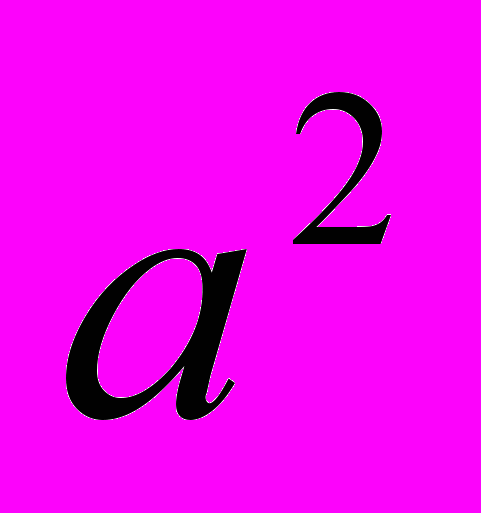Вариант 12
  1. Погорелов. Геометрия 7-11, 79 стр., задача 32.
  2. Атанасян. Геометрия 7-9, 212 стр., задача 876.
  3. Метод движения. Суть метода. Построение образа отрезка при повороте, параллельном переносе и осевой симметрии.


4.3. Варианты контрольной работы по курсу

Вариант 1
  1. Построить треугольник по основанию, высоте и боковой стороне.
  2. Построить треугольник, если известны .
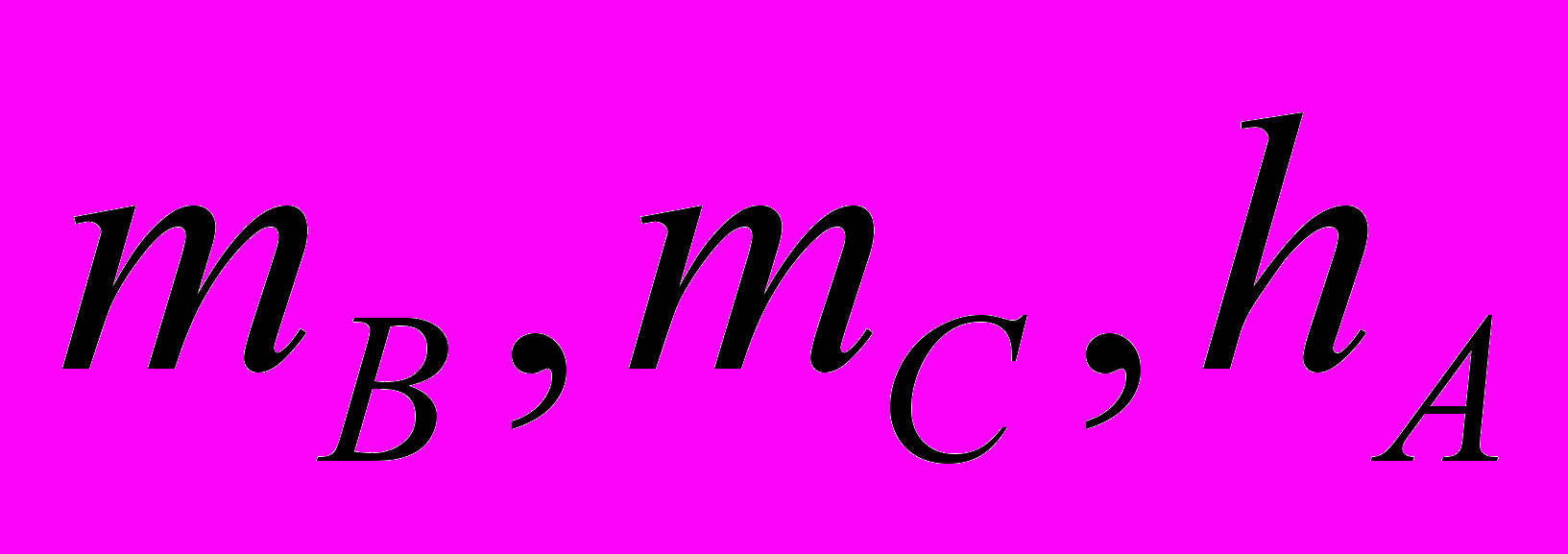  3. Построить отрезок по формуле .


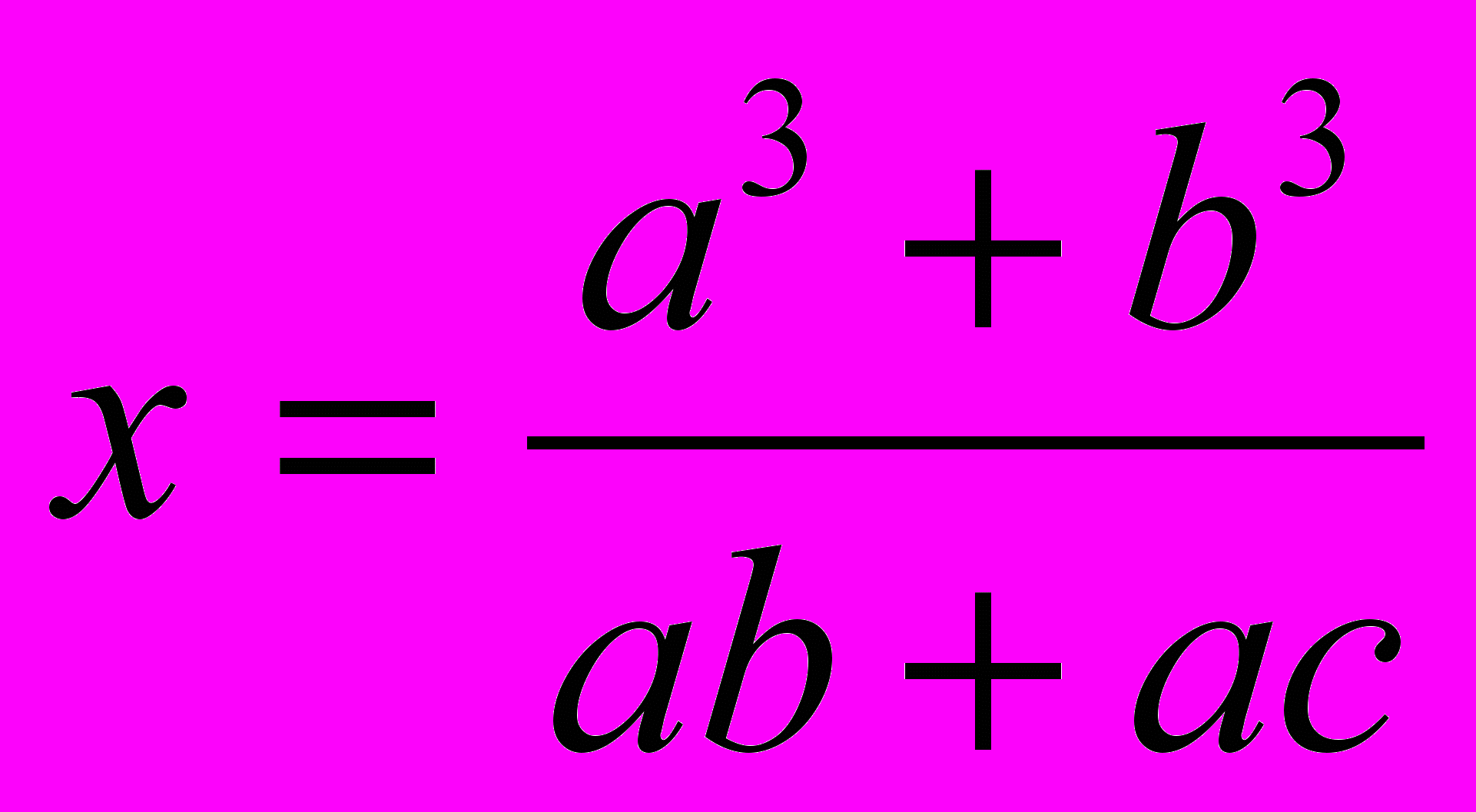Вариант 2
  1. Построить треугольник по основанию, высоте и медиане, проведенной к боковой стороне.
  2. Построить треугольник по высоте, разности отрезков, на которые она делит основание, и разности углов, прилежащих к основанию.
  3. Построить квадрат, площадь которого была бы равна сумме площадей двух данных прямоугольников.


Вариант 3
  1. Построить треугольник по основанию, высоте и радиусу описанной окружности.
  2. Построить четырехугольник, зная 4 стороны, если известно, что одна диагональ делит угол пополам.
  3. Провести прямую, которая одновременно делила бы пополам площадь и периметр данного треугольника.


Вариант 4
  1. Построить окружность, которая касалась бы данной окружности в данной точке и данной примой.
  2. Построить четырехугольник по диагоналям, углу между ними и двум смежным его сторонам.
  3. Разделить трапецию на две равновеликие части, проводя прямую, параллельную основанию.


Вариант 5
  1. Построить окружность данного радиуса, проходящую через данную точку и отсекающую от данной прямой хорды данной длины.
  2. Построить треугольник по двум сторонам и разности противолежащих им углов.
  3. В данный круг вписать прямоугольник, равновеликий данному квадрату.


Вариант 6
  1. Внутри данного треугольника построить точку, из которой его стороны были бы видны под равными углами.
  2. Построить прямоугольный треугольник, у которого один катет вдвое больше второго, а высота, опущенная на гипотенузу равна данному отрезку. (гомотетия)
  3. Построить отрезок по формуле .


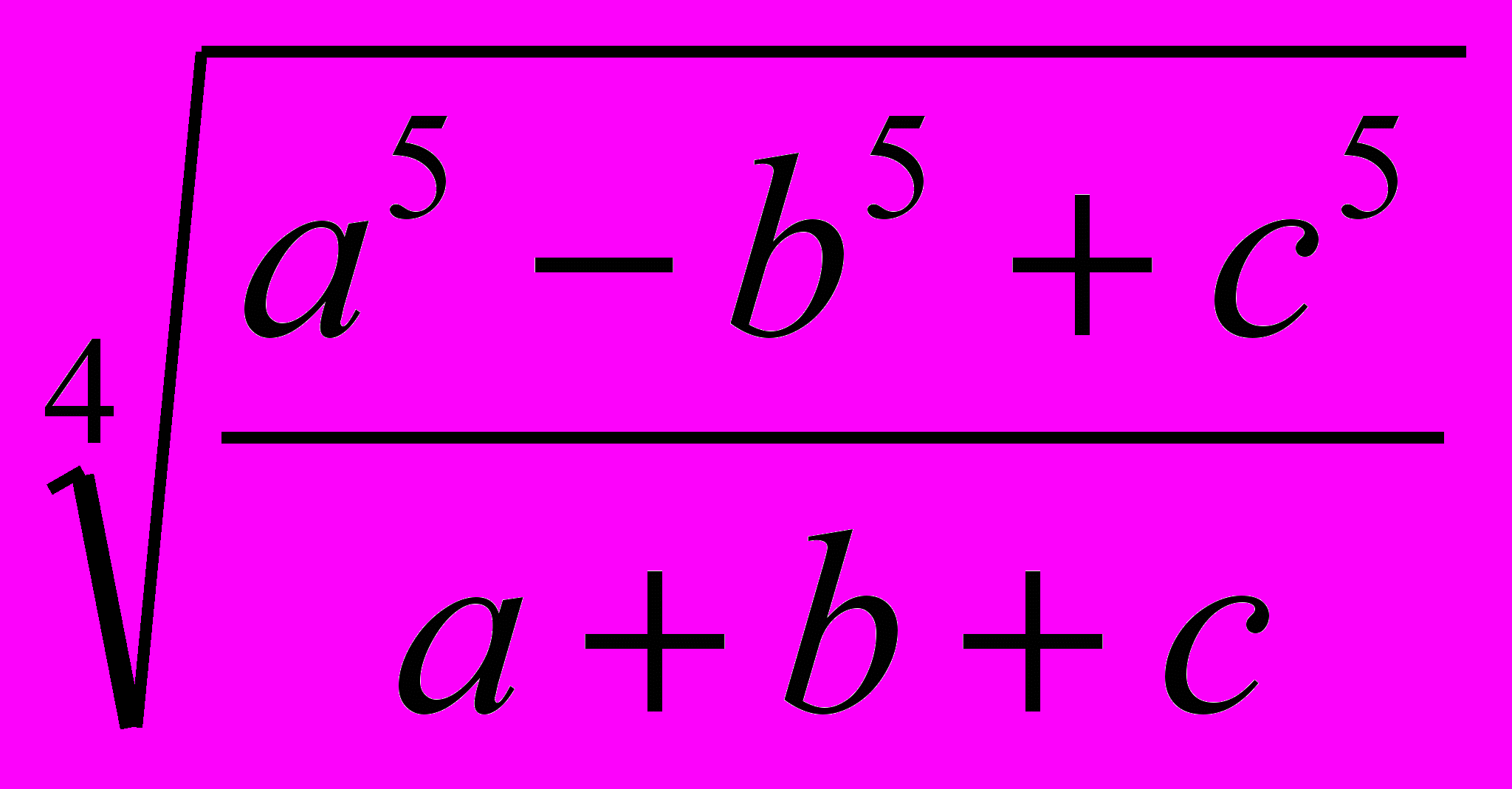Вариант 7
  1. Построить ромб по стороне и радиусу вписанной окружности.
  2. Построить параллелограмм, основанием которого служит данный отрезок, а две другие его вершины лежат на двух данных окружностях.
  3. Построить угол , зная, что .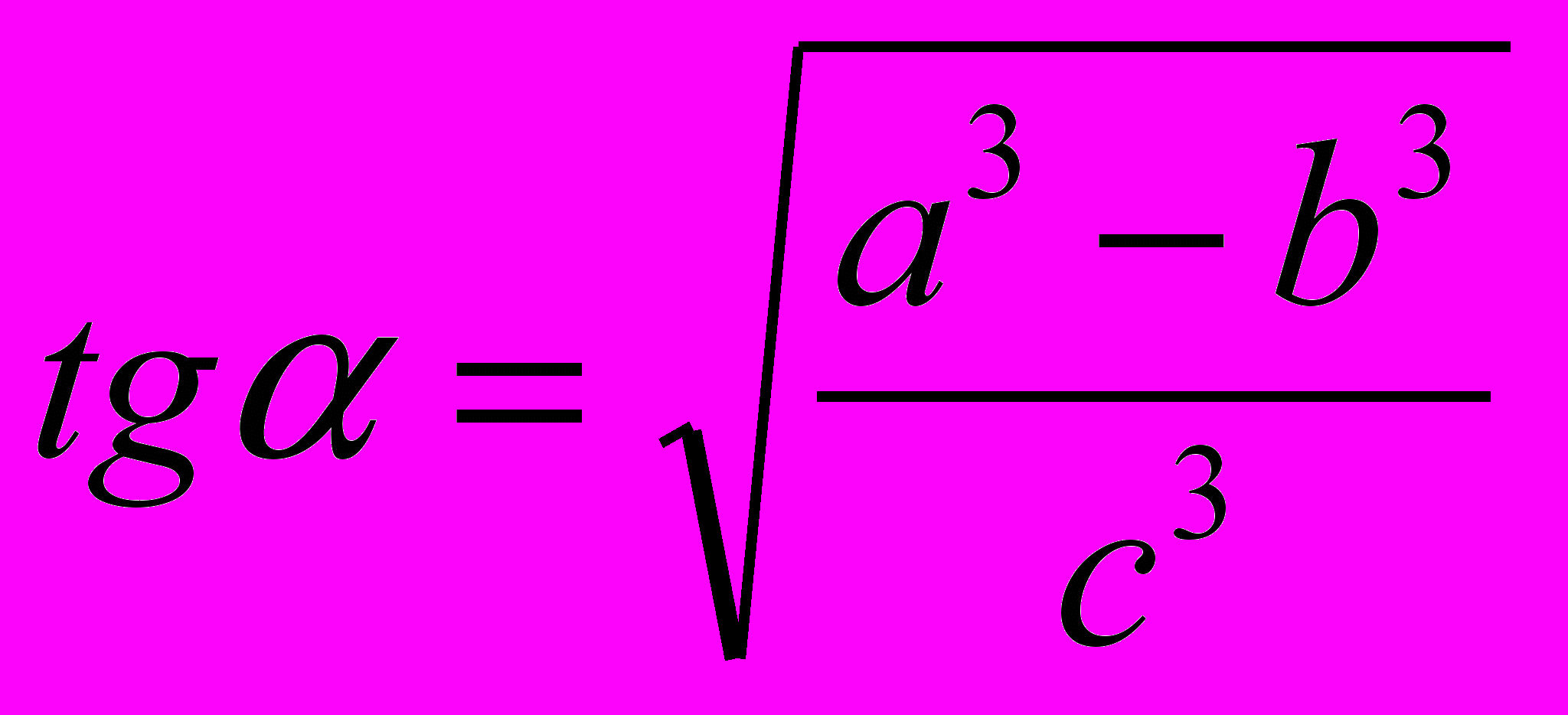


Вариант 8
  1. Построить окружность данного радиуса, касающуюся данной окружности и данной прямой.
  2. В данную окружность вписать прямоугольник данного периметра.
  3. В данную окружность вписать треугольник, если даны точки пересечения его биссектрис с окружностью.


Вариант 9
  1. Построить треугольник по основанию, высоте и отношению боковых сторон.
  2. Построить окружность, проходящую через данную точку и касающуюся двух данных окружностей. (инверсия)
  3. Построить отрезок по формуле .


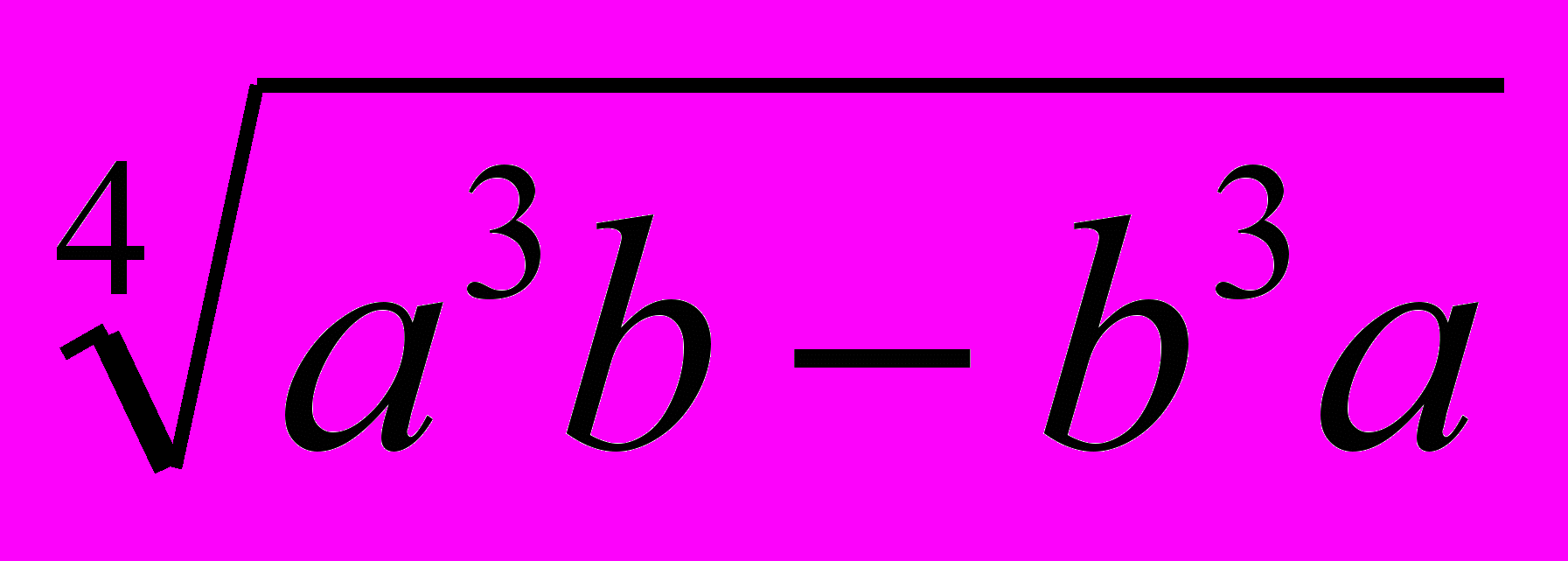Вариант 10
  1. Даны три точки 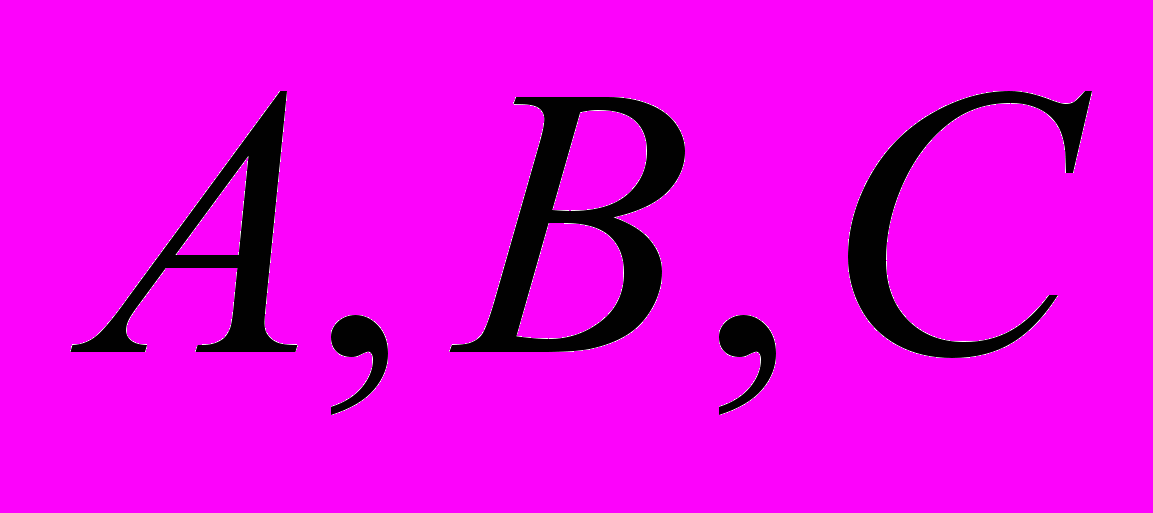. Провести через окружность так, чтобы отрезки касательных к ней из точек 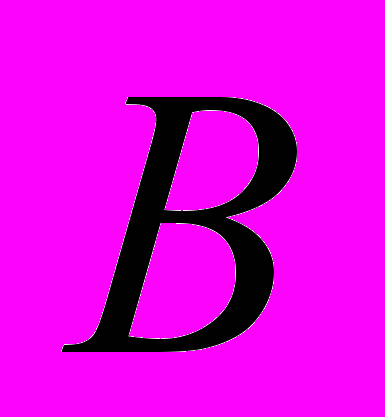и были бы соответственно равны данным отрезкам 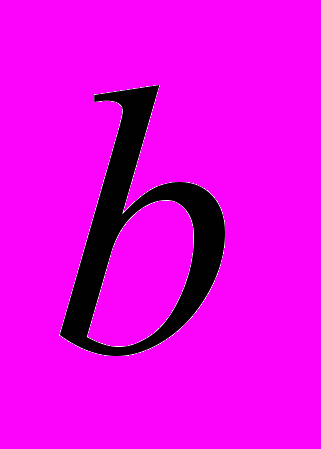и .
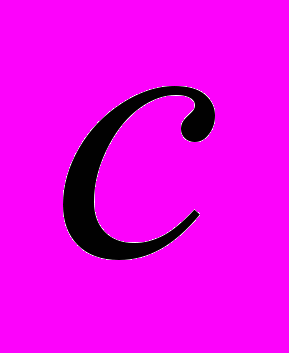  2. Построить четырехугольник, зная четыре его стороны и угол между двумя противоположными его сторонами.
  3. Дан единичный отрезок. Построить, длина которого была бы равна .


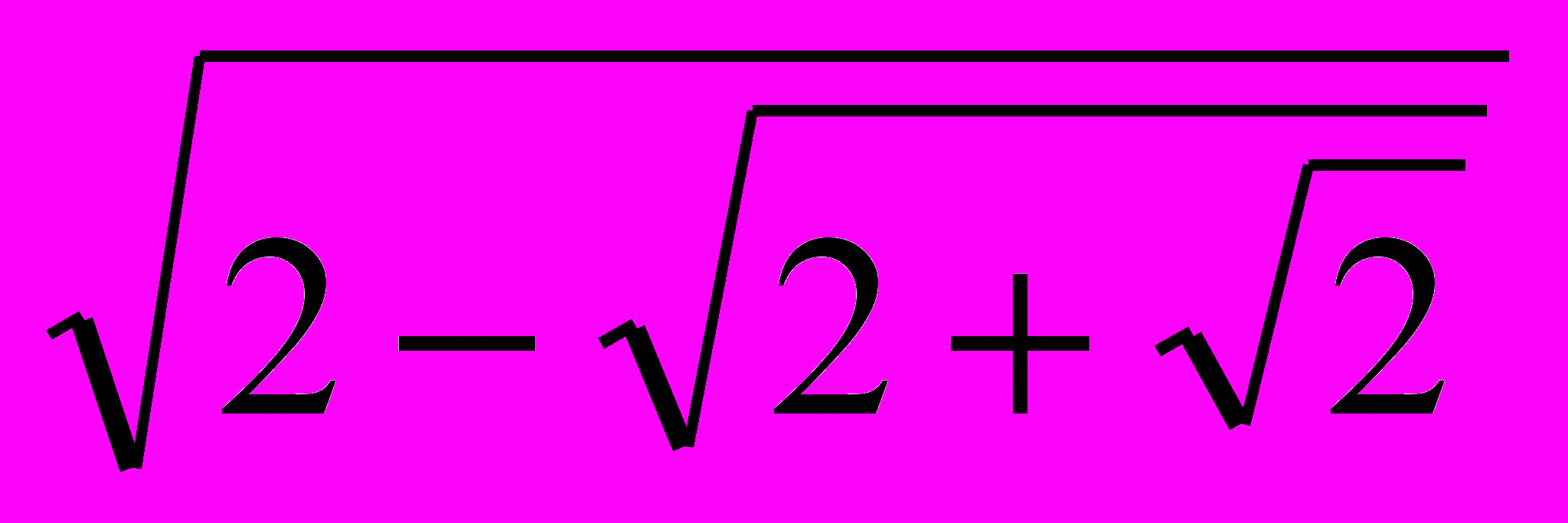Вариант 11
  1. Найти такую точку, чтобы касательные, проведенные из нее к двум данным окружностям, были равны ее расстоянию от данной точки.
  2. В данный параллелограмм вписать квадрат.
  3. Построить угол , зная, что .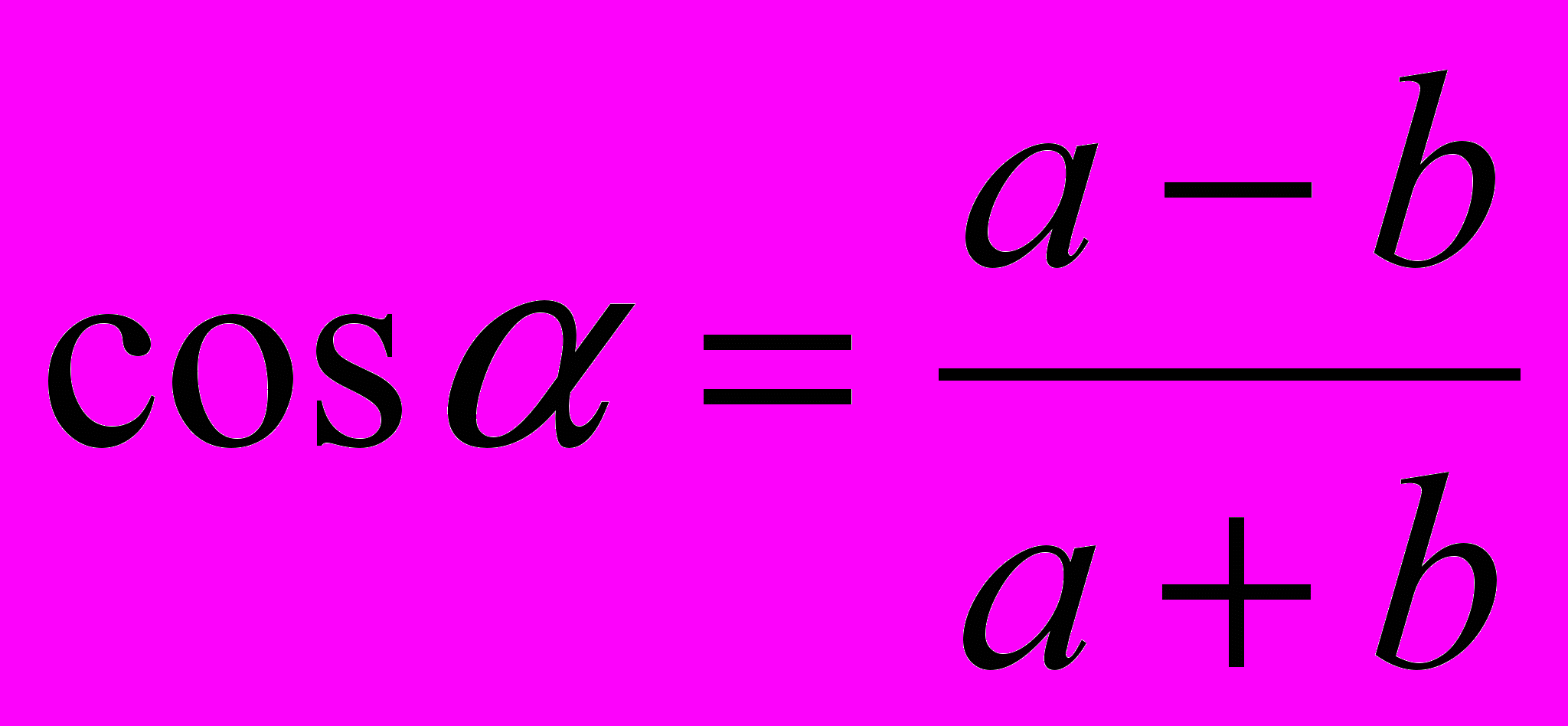


Вариант 12
  1. Построить треугольник 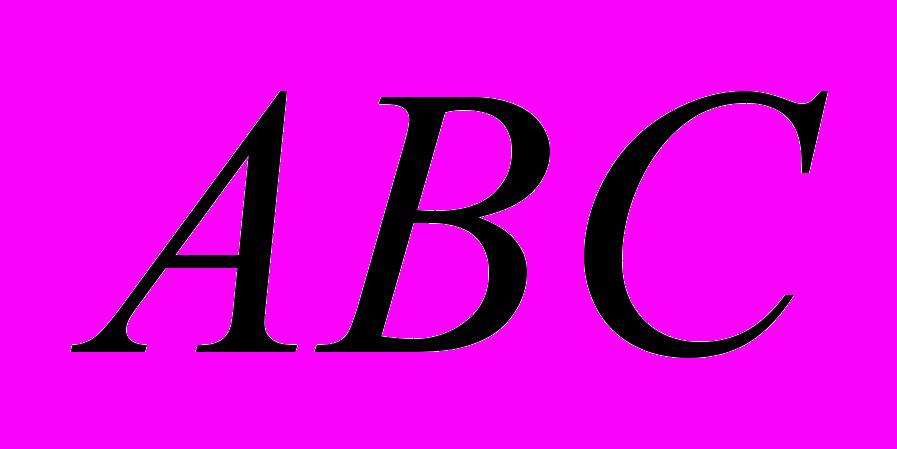по углу , стороне 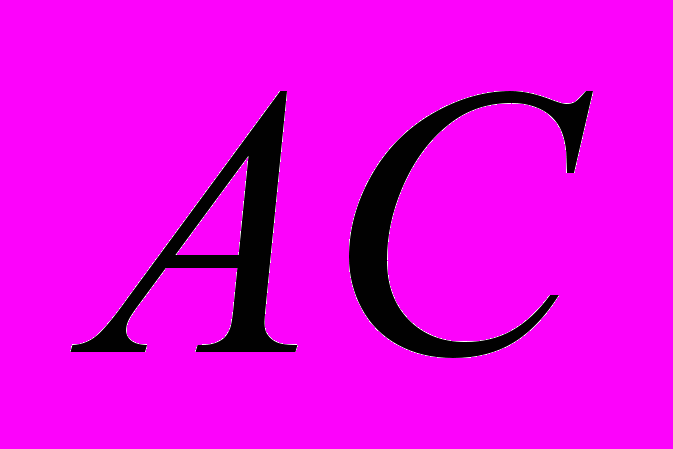и высоте .
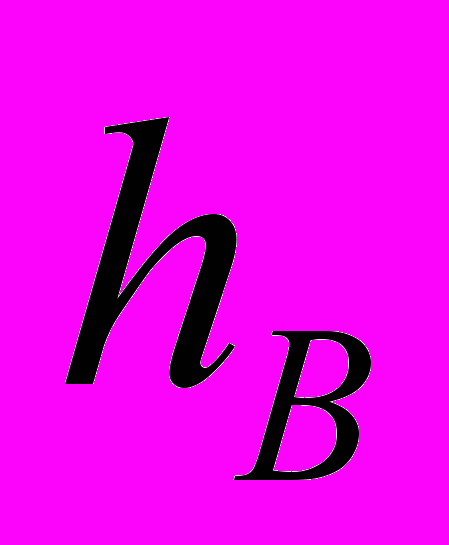  2. Построить прямоугольный треугольник, у которого один катет вдвое больше второго, а гипотенуза равна данному отрезку. (гомотетия)
  3. Построить треугольник по трем высотам.


Вариант 13
  1. Построить треугольник по основанию, высоте и боковой стороне.
  2. Построить треугольник, по отношению двух сторон, острому углу, противоположному одной из них и медиане, исходящей из этого угла.
  3. От данного квадрата отсечь одинаковые прямоугольные треугольники так, чтобы образовался правильный восьмиугольник.


Вариант 14
  1. Построить треугольник по основанию, высоте и медиане, проведенной к боковой стороне.
  2. В данный треугольник вписать прямоугольник, у которого одна сторона в три раза больше второй. (гомотетия)
  3. Построить окружность, проходящую через две данные точки и касающуюся данной прямой.



Вариант 15
  1. Построить треугольник по основанию, высоте и радиусу описанной окружности.
  2. Через данную точку провести окружность, пересекающую две данные прямые под данными углами. (инверсия)
  3. Построить квадрат, площадь которого была бы равна сумме площадей двух данных прямоугольников.


Вариант 16
  1. Построить окружность, которая касалась бы данной окружности в данной точке и данной примой.
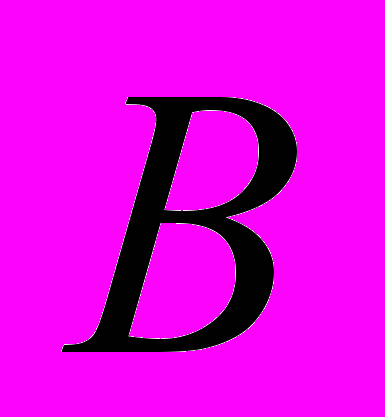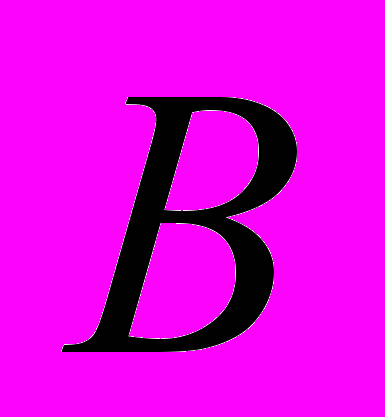  2. Между пунктами и расположены два канала. Где выбрать места для мостов через эти каналы, чтобы путь из в через эти мосты был кротчайшим? (Предполагается, что берега каналов – параллельные прямые и что мосты должны быть перпендикулярны берегам.)
  3. Построить угол , зная, что .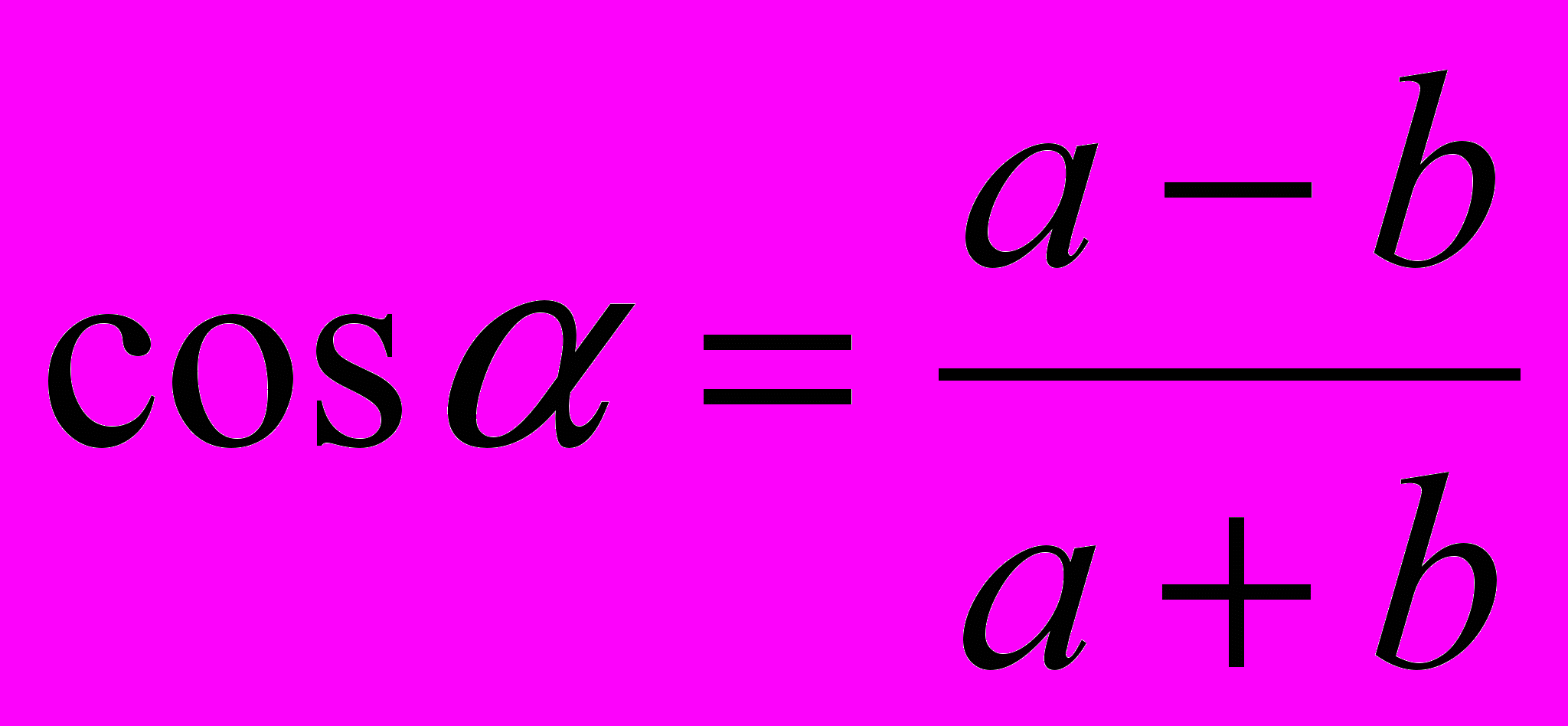


Вариант 17
  1. Построить окружность данного радиуса, проходящую через данную точку и отсекающую от данной прямой хорды данной длины.
  2. Построить прямоугольный треугольник, у которого один катет вдвое больше второго, а сумма катетов и высоты, опущенной на гипотенузу, равна данному отрезку. (гомотетия)
  3. В данную окружность вписать прямоугольник данного периметра.


Вариант 18
  1. Внутри данного треугольника построить точку, из которой его стороны были бы видны под равными углами.
  2. Вписать в данную окружность равнобедренный треугольник, зная отношение основания к боковой стороне. (гомотетия)
  3. Построить угол , зная, что .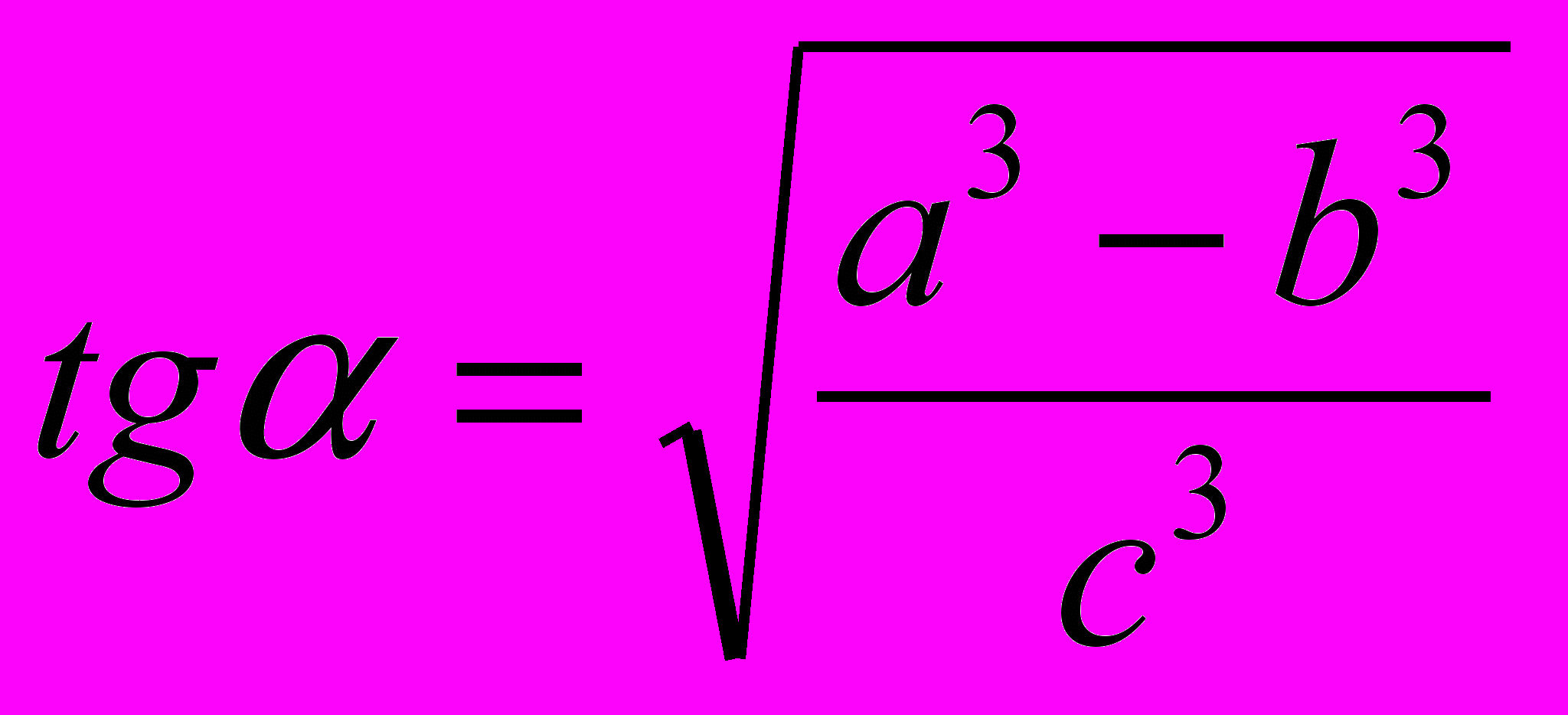


Вариант 19
  1. Построить ромб по стороне и радиусу вписанной окружности.
  2. Построить треугольник по основанию, высоте и боковой стороне.
  3. Построить отрезок по формуле .



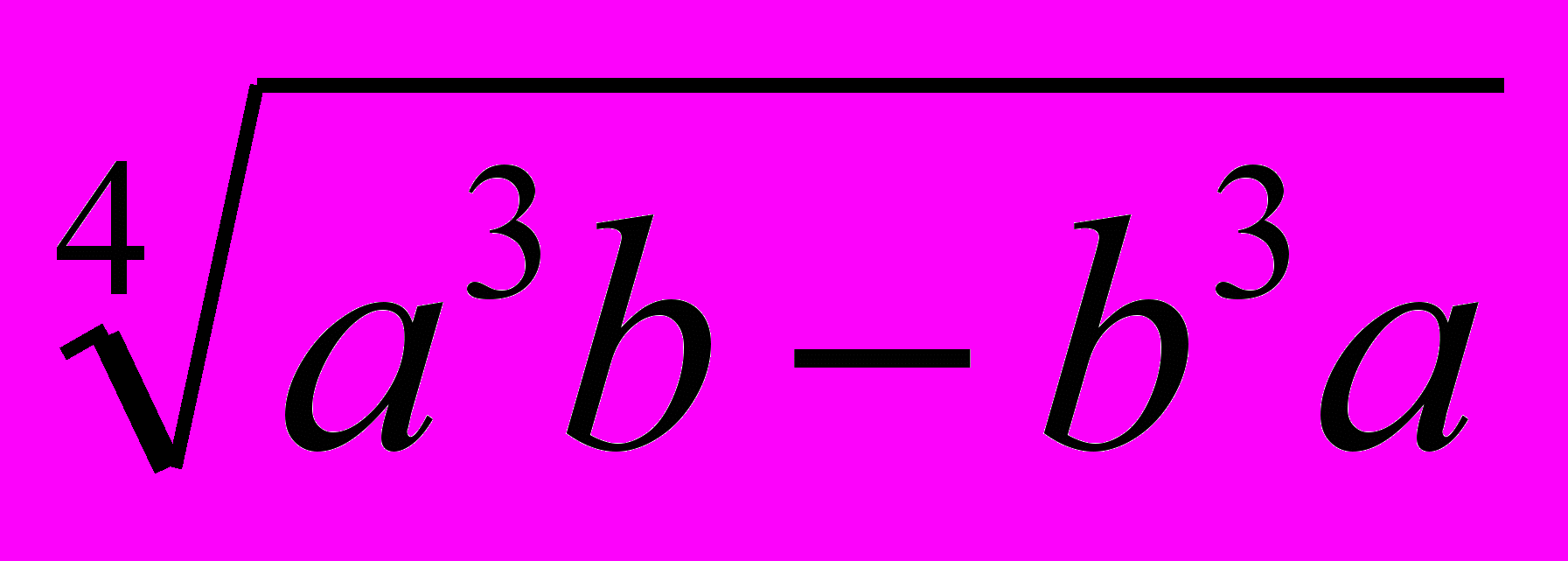Вариант 20
  1. Построить треугольник по основанию, высоте и отношению боковых сторон.
  2. Построить четырехугольник, зная 4 стороны, если известно, что одна диагональ делит угол пополам.
  3. Построить отрезок по формуле .



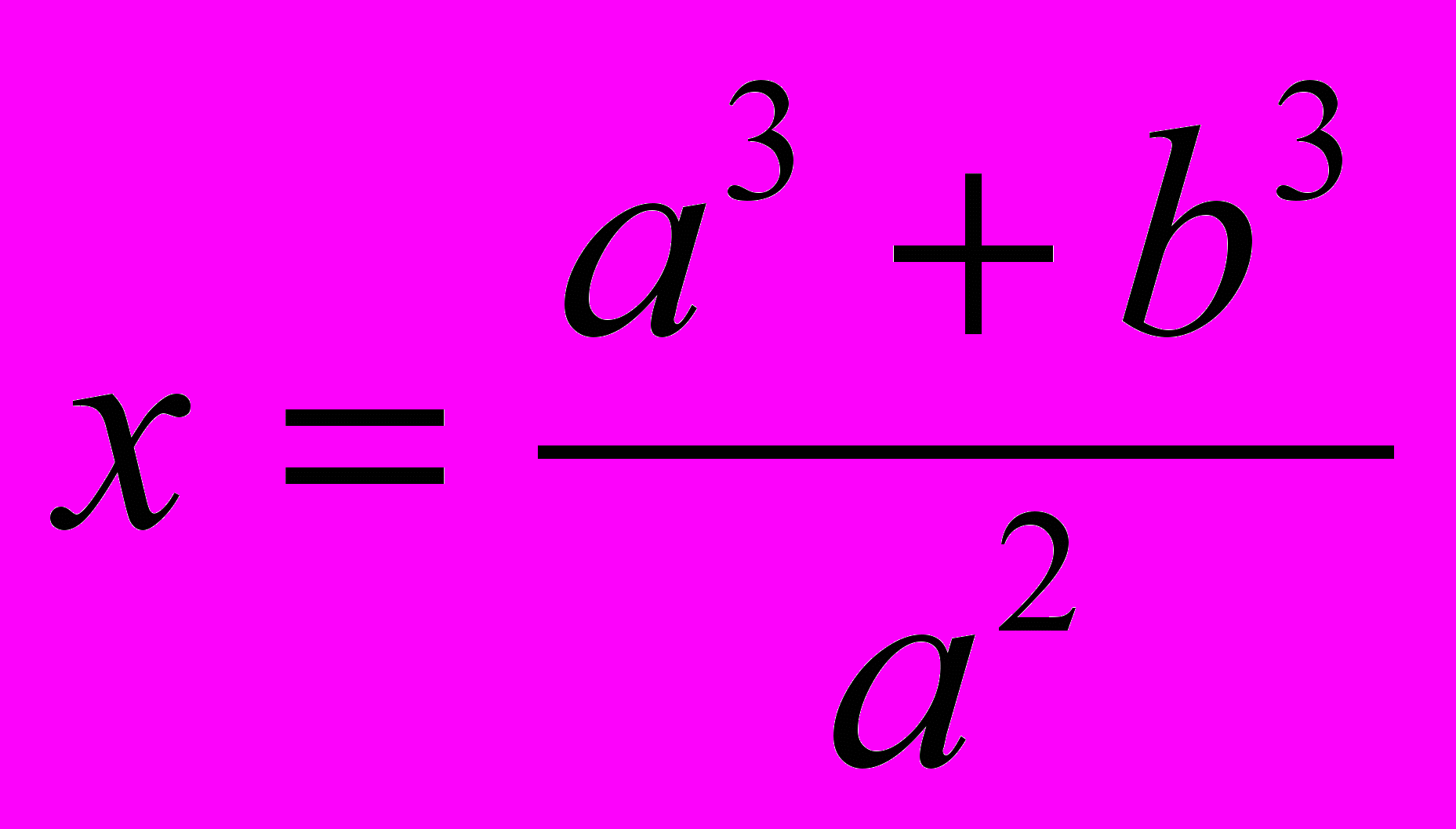5. Методические рекомендации студентам

После изучения теоретического материала Вы должны:
    • овладеть основными построениями
    • овладеть основами конструктивной геометрии
    • знать аксиомы и постулаты конструктивной геометрии
    • овладеть методами решения задач на построения с помощью циркуля и линейки

По окончании практического курса Вы должны:

- овладеть основными методами решения задач на построение с помощью циркуля и линейки


6. Формы текущего, промежуточного и итогового контроля.

Текущий контроль:

- Самостоятельные работы

- Индивидуальные задания

- Опрос студентов

Промежуточный контроль:

- Коллоквиум по ГМТ

- Индивидуальная работа по школьным учебникам

- Контрольная работа по курсу

Итоговый контроль:

- Зачет


7. Список литературы
  1. Аргунов Балк. Геометрические построения на плоскости.
  2. Атанасян Л.С., Базылев В.Т. Геометрия. В 2-х частях. Ч. I. Учебное пособие для студентов физ.-мат. фак. пед. институтов. – М.: Просвещение, 1986.
  3. Атанасян Л.С. и др. Геометрия 7-9. – М.: Просвещение, 1994.
  4. Погорелов А.В. Геометрия 7-11. – М.: Просвещение, 1992.