Открытие сделано подтверждено экспериментом, что дальше…?

1   2   3   4

Но вот Оннес открыл НТСП. Однако, из-за невысокой точности измерения величины электрического сопротивления сверхпроводника (СП) он пришел к выводу, что оно в СС равно нулю. Позже, при существенном повышении точности измерений, ученые пришли к выводу, что сопротивление СП имеет очень маленькую, но конечную величину. Сейчас его называют или остаточным, или примесным сопротивлением СП [22].

Данное понятие просто и наглядно может быть интерпретировано формулой (4.11). Дело в том, что сопротивление СП только потому не равно нулю, что R₂ не равно нулю.

Получается, что сопротивление проводника в СС, на мой взгляд, – это в чистом виде проявление эффекта взаимодей-ствий (столкновений) электронов в е-газе двух групп между собой. Не исключено, что эти взаимо-действия как раз и ведут к образованию истинных фононов или ротонов в кристаллической решетке проводников. Однако, этот процесс сейчас интерпретируют как эффект сопровождающий процесс образования так называемых "куперовских пар", которые якобы полностью объясняют сущность НТСП.

О куперовских парах подробно будет сказано ниже.

Итак, для пояснения сказанного выше с целью, например, анализа зависимости изменения электрического сопротивления проводника от его температуры исследуем три графика на рис.4.2 с учетом существования пороговой энергии (4.9, 4.10) для двух групп электронов в е-газе. Как видно из кривой 3 на рис.4.2 площадь под ней, лежащая слева от вертикальной прямой 1-1 существенно больше площади справа. А это значит, что n_ >> n_Т, поэтому электрическое сопротивление проводника много меньше, чем при нормальных условиях (кривая 1). И наоборот. При нагревании проводника n_Т >> n_, кривая 2, поэтому его электрическое сопротивление существенно больше чем при нормальных условиях (кривая 1).

Изменение величины сопротивления проводника в процессах его охлаждения и нагревания происходит за счет изменения плотности, но не количества свободных электронов n₀ в е-газе. Это изменение плотности (концентрации) в основном происходит из-за изменения объема проводника или, что то же самое, объема квантовых ячеек. При охлаждении они сжимаются и концентрация электронов увели-чивается. При нагревании они расширяются и концентрация электронов уменьшается. Такое толкование процесса зависимости сопротивления от температуры не согласуется с общепринятым его объясне-нием, скажем в учебнике И.Е. Тамма "Основы теории электричества" (М., "Наука", 1976).

В нем утверждается, что величина электропроводности в зависимости от температуры проводника определяется только длиной свободного пробега электронов, поскольку концентрация (плотность) электронов n₀ температуры проводника практически не зависит.

Да, число электронов (n₀) действительно от температуры в данном случае не зависит, но объем то квантовых ячеек изменяется, причем весьма заметно.

Наглядным примером такого механизма изменения УЭП являются генераторы сверхсильного импульсного магнитного поля (СИМП), описанные, например в [3].

В сжимаемом под действием взрыва лайнере резко уменьшаются объемы квантовых ячеек. Ток прово-димости скачком сильно увеличивается и создает мощный импульс СИМП, а сам лайнер разрушается от джоулева тепловыделения от этого импульса тока!

И еще, различие размеров квантовых ячеек различных металлов скажем в термопарах, а следовательно и концентраций е-газа в них, вызывает за счет градиента концентрации контактную разность потенциалов или электродвижущую силу (ЭДС).

В то же время, при этой температуре, скорость дрейфа, обусловленная максимально допустимой плот-ностью тока для материала этого же проводника, равна 0,01м/с. Таким образом, подставляя известные величины в (4.19), получаем, что УЭП металлов на порядок величины лежит в диапазоне от 10⁷ до 10⁸ Ом^-1  м^-1. А это весьма удовлетворительно совпадает с табличными значениями УЭП, приведенными, например, в [4, 28].

Теперь, если мы оценим величину УЭП таким же способом для того же проводника, но заведомо нахо-дящегося в СС, предварительно, например, для 1^оК, оценив скорость теплового движения электронов по (4.20), и зная, что скорость дрейфа при НТСП возрастает до 1м/с [29], то получаем, что (4.19) ≈ 10⁴.

Известно, что при НТСП получать еще большие скорости дрейфа нельзя, поскольку СС у СП "разрушается" (исчезает) из-за появления так называемой критической напряженности магнитного поля, возникающего от тока текущего по СП.

Получается, что снижение величины УЭП за счет увеличения скорости дрейфа и снижения величины тепловой скорости электронов проводимости в совокупности на три порядка привело к величайшему открытию в физике. Только на этом основании к проводимости была присоединена приставка "СВЕРХ".

Однако, парадоксальность ситуации заключается в том, что на самом-то деле электрическое сопроти-вление проводника увеличилось. Кстати, данный парадокс подтверждают металлокерамические проводники, на которых получено СС, например, при 100К. А это значит, что физический смысл НТСП заключается в том, что несмотря на уменьшение УЭП в проводнике просто возрастает концентрация

е-газа за счет уменьшения (сжатия по трем направлениям) объема квантовых ячеек. Т.е. резко умень-шается величина R1 в формуле (4.11). Этот факт дает обоснование одного из путей повышения кри-тической температуры проводников путем увеличения каким-либо физико-химическим способом кон-центрации свободных электронов в проводнике, либо уменьшения размеров квантовой ячейки в сверхпроводящих композитах.

Чтобы понять и определить общность соотношения (4.19) и распространить его, скажем на плазму, используя данные табл.1, оценим его величину для веществ ЕПТ: БК, НЗ, Солнца и ядер ШМ. Вычисления показали, что для вещества канала линейной молнии (ЛМ) и ядер ШМ оно равно 1,0, для вещества НЗ - 0,1, для БК - 50, для вещества Солнца - 350. СТОП! Но ведь по крайней мере вещество НЗ и БК находится в СС [6]. Следовательно, учитывая изменение (4.19) для проволочки с током, находящейся как при температуре 273К, так и при 1К, мы можем сделать вывод, что все электропроводные вещества, для которых величина соотношения (4.19) лежит в диапазоне от 10000 до 0,1 должны находиться в СС, причем при любой температуре, начиная с "абсолютного нуля" и кончая, скажем миллиардом градусов Кельвина.

Невероятно, но факт. Получилось, что соотношение (4.19) имеет очень глубокий физический смысл потому, что оно характеризует СС практически любых веществ, в любых их физических и фазовых состояниях и, конечно, при любых температурах. Именно к этому результату привели исследования практически забытой модели Друде-Лоренца и соотношение (4.8).

(4.19) (Ig) соответствует параметрам «Золотого Сечения», является универсальным критерием (УК), оценки СС любых веществ, при любых температурах и состояниях.


О КУПЕРОВСКИХ ПАРАХ (сокращена)


ДИНАМИЧЕСКАЯ СВЕРХПРОВОДИМОСТЬ не зависит от температуры!?


Прогноз существования эффекта динамической сверхпроводимости ДСП в быстровращающихся электропроводных телах (диски, кольца, маховики и т.д).

Основу эффекта составляет известный опыт Толмена-Стюарта, проведенный ими в 1916 г. под руко-водством Лоренца. Был обнаружен эффект динамической проводимости металлических проводников.


Цель опыта заключалась в определении частицы-носителя электрического тока в металлах [4]. Для его проведения была изготовлена катушка с большим числом витков тонкой медной проволоки. Катушку, приводили в быстрое вращение. Средняя линейная скорость вращения обмотки составляла 300 м/с.

С помощью специального приспособления катушку резко останавливали.

Опыты впервые показали, что носителем электрического тока в металлах являются электроны е-газа. Найденное отношение величины заряда электрона к его массе в электродинамике стало со временем фундаментальной физической постоянной, которая имеет широкое применение как в теоретической, так и в экспериментальной физике.

Сравним между собой два физических объекта: быстро вращающуюся катушку Толмена-Стюарта и быстро вращающийся диск - у них есть много общего.

Диск похож на катушку, но только одновитковую, причем короткозамкнутую. Виток - контур при раскрутке, как виток с током должен генерировать магнитное поле, как в (магнитомеханическом) эф-фекте, открытым в 1915 г. Гаазе-Эйнштейном, но существенно более интенсивное. Здесь дело заклю-чается в том, что на свободные электроны нашего коротко замкнутого витка кроме силы (4.27), при его ускорении, т.е. раскрутке, действует еще и центробежная сила инерции:

В опытах Толмена-Стюарта сила (4.30) практически не играла никакой роли на конечный результат опыта только потому, что при диаметре проволоки, скажем, равном 0,001 м, она была исчезающе мала и направлена не вдоль, а поперек микроскопического сечения проволоки. Однако, в быстро вращающемся электропроводном диске, скажем диаметром 1,0 м, дело обстоит иначе. Ведь рассматриваемый диск - классическая центрифуга [44] для е-газа, омывающего кристаллическую решетку материала диска.

Под действием силы (4.31, 4. 32, 4.33) электроны из объема монолитного диска, двигаясь по спирали, будут сепарироваться и накапливаться во внешнем очень тонком слое обода диска, скажем толщиной порядка 10^-5 см. Обод - тонкий слой материала диска, имеющий максимальное значение величины линейной скорости его вращения. Такая толщина слоя проводимости, например, характерна для слоя проводимости у проволочки, по которой течет ток при НТСП. Следовательно, при раскрутке диска при увеличении частоты вращения в этом слое будет расти концентрация е-газа и, соответственно, коль-цевой, замкнутый сам на себя, ток проводимости, причем направленный против вращения диска. Этот эффект проявится в некотором нагревании обода диска, а при большой скорости вращения не исклю-чено и испарение материала обода диска. Рост силы этого тока со временем обусловлен следующими причинами:

первая - увеличение скорости дрейфа, т.е. "проскальзывания" электронов относительно кристаллической решетки материала обода диска (эффект или ток Толмена-Стюарта);

вторая - собственно увеличение концентрации е-газа в ободе диска, входящая, например, в формулу (4.25), по сравнению с концентрацией в покоящемся диске (или на оси вращения диска), причем этот эффект однозначно ведет к увеличению УЭП только материала обода диска, а следовательно и к росту в нем максимально допустимой плотности тока.

Последнее ведет к тому, что максимально допустимая плотность тока для одного и того же материала обода раскручиваемого диска становится существенно большей, чем для покоящегося диска. Получается, что данный эффект фактически подобен (или даже эквивалентен) эффекту увеличения УЭП при охлаждении всего диска, скажем, до температуры жидкого гелия, но уже без образования куперов-ских пар, существование которых, как было показано выше, - весьма проблематично.

По аналогии с НТСП теоретически установленный эффект был назван эффектом динамической сверх-проводимости ДСП, это начальная фаза образования эффекта. Она подразделяется на три этапа «разгона», энергетических «скачков» электронной плотности при «сепарации», установившийся режим ССМП и его напряженности на 1-ом, 2-ом или 3-ем «скачке», назван короткозамкнутый тороидальный электронный жгут (вихрь) или КОРТЭЖ. Форма и кчественная оценка установившегося «электронного жгута», ССМП, напряженность, будет описана в следующих главах моей книги, с прогнозом применения ССМП в прикладных свойствах проекта МАГФ.


ХАРАКТЕРИСТИКИ «ЛЕТАЮЩИХ» ДИСКОВ.


Используя для е-газа, термодинамические соотношения для идеального газа, при комнатной темпе-ратуре (300 К), оценим, в зависимости от частоты вращения диска, его некоторые электродинамические характеристики.

Оценим давление е-газа в объеме покоящегося диска.

При Т (300 К), в зависимости от материала диска величина (4.34) лежит в диапазоне от 10⁸ до 10⁹ Н на квадратный метр или от 1000 до 10000 атм. При раскрутке диска с ускорением:

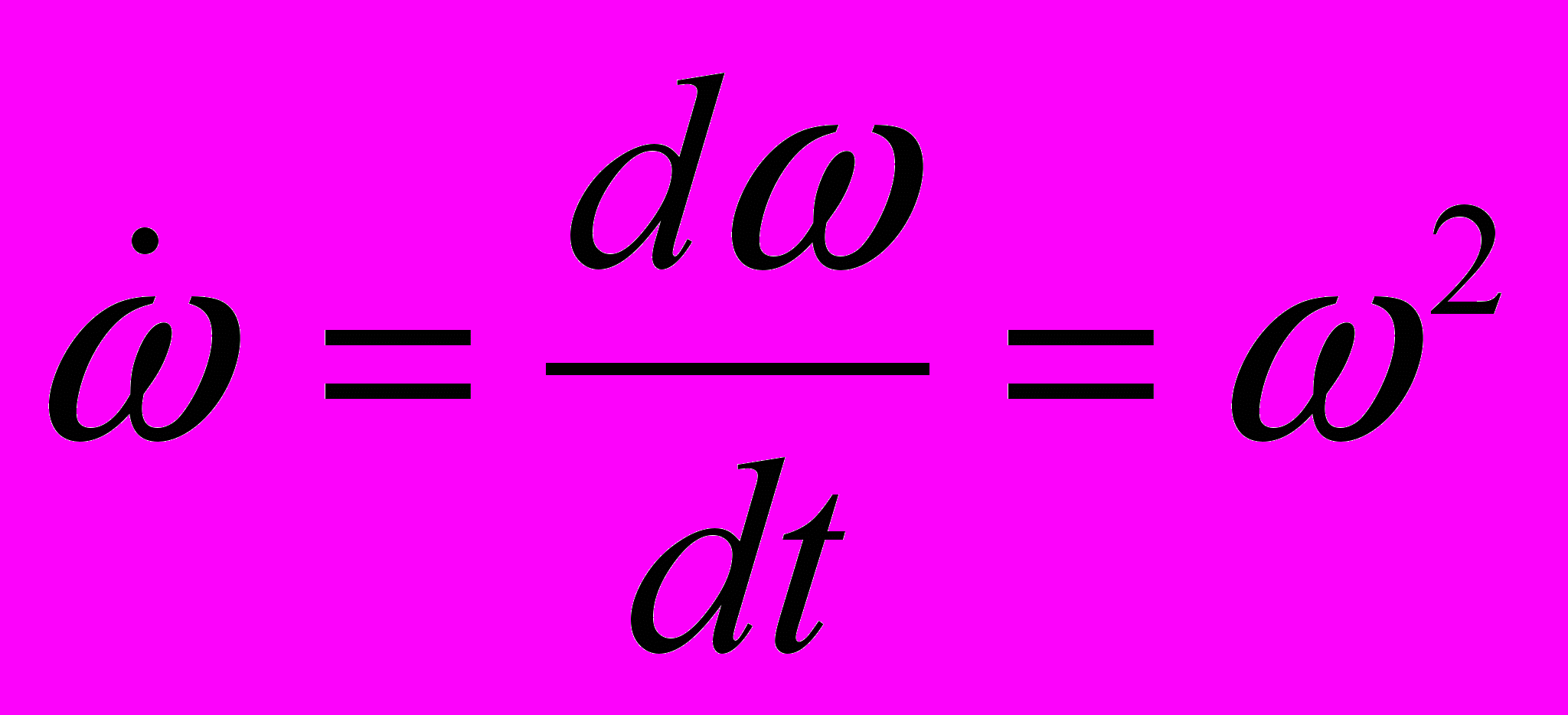(4.35)

В ободе под действием равнодействующей силы инерции (4.32) или (4.33) величина давления е-газа должна увеличиваться за счет увеличения частоты вращения. Чтобы оценить это увеличение воспользуемся расчетной схемой, приведенной на рис.4.4.

Понятно, что в покоящемся диске давление е-газа во всех точках его объема:

(4.36)

- постоянно и одинаково, а его объемный электрический заряд скомпенсирован объемным зарядом ионов, образующих кристаллическую решетку материала диска. Поэтому электрический ток в диске, отсутствует.

Раскручиваем диск с ускорением (4.35),то в е-газе появится градиент давления за счет того, что на каждый электрон в нем будет действовать сила (4.32) или (4.33). А это значит, что между осью вращения диска, где будет возникать некоторое разрежение е-газа, и его ободом за счет сепарации электронов в нем появится изотропное электрическое поле с напряженностью поля сторонних объе-мных сил инерции:

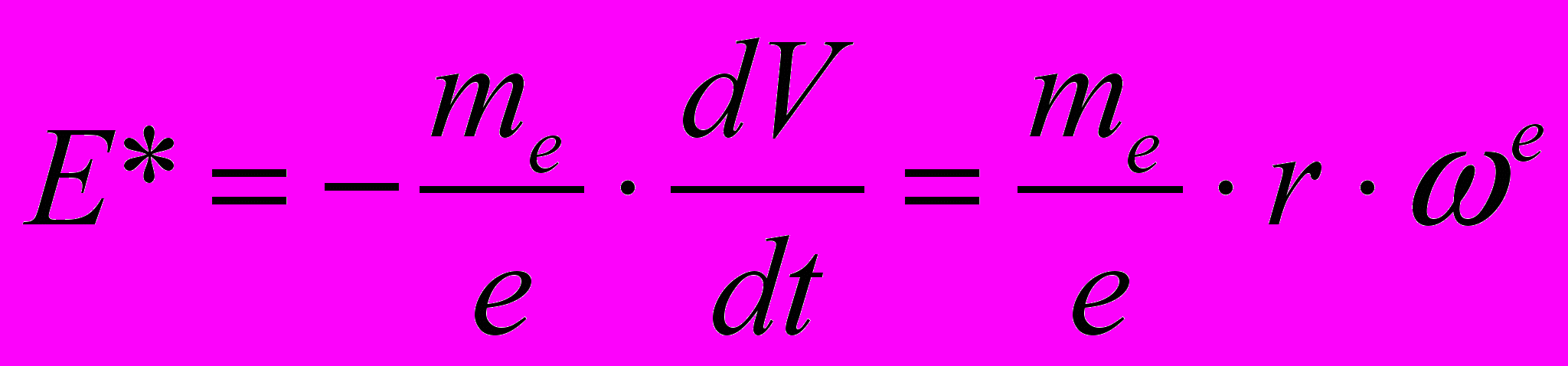. (4.37)

Следовательно, между осью вращения диска и его ободом появится электродвижущая сила (ЭДС).

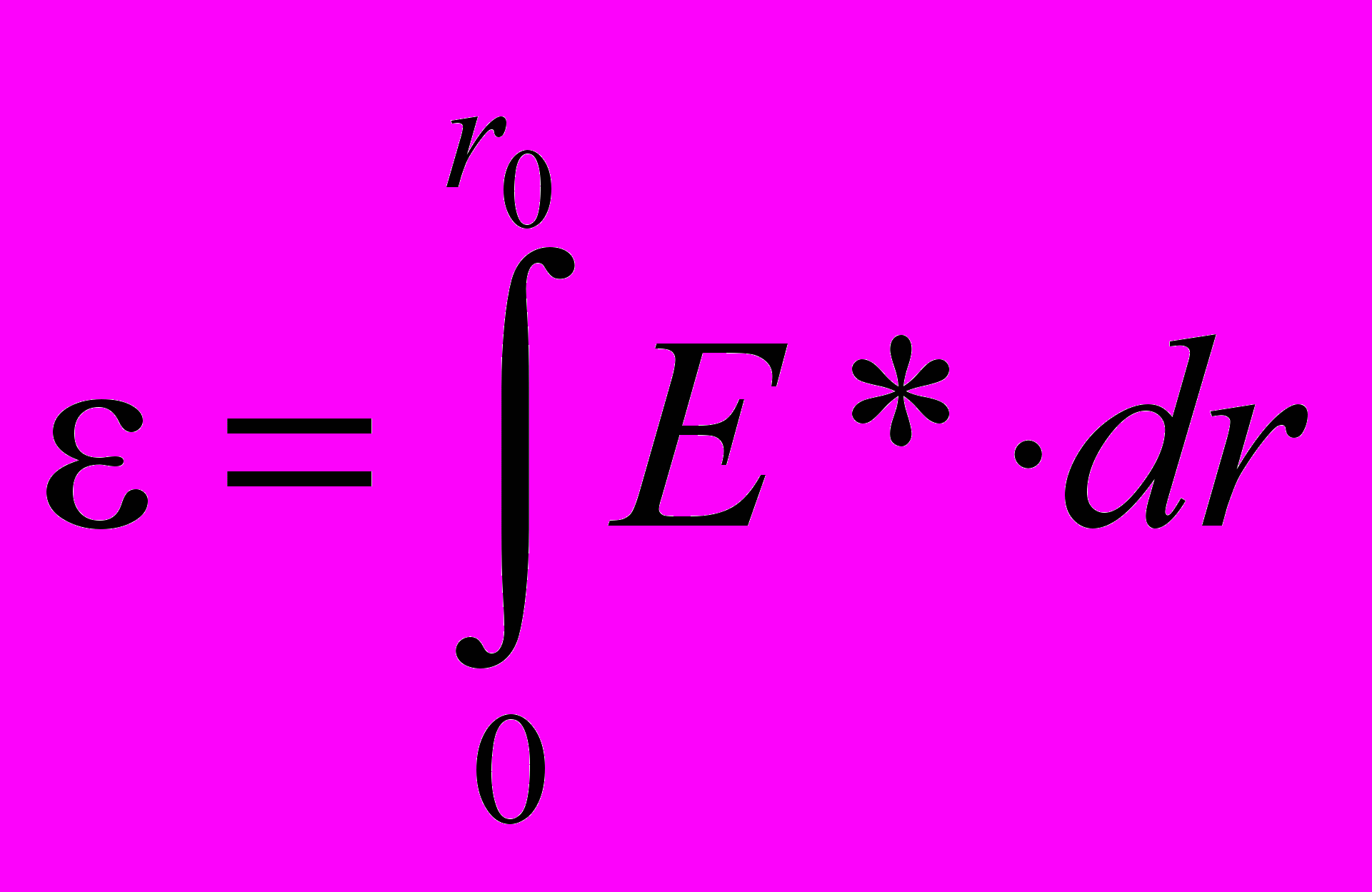. (4.38)

Эту ЭДС экспериментально обнаружил Серл [7.21]. Малая величина (4.38) говорит о том, что ЭДС измерялась, во первых, в короткозамкнутом "витке", ободе быстровращающегося электропроводного диска, а во вторых, ее расчет сделан на 1 электрон е-газа. Обод - тонкий слой материала диска, имею-щий максимальную линейную скорость его вращения.

Начнем с того, что с учетом (4.37) проинтегрируем (4.38). В результате получаем:

(4.39)

где: Г=1.76 х 10¹¹ кл/кг - гидромагнитное отношение для электрона - фундаментальная физическая постоянная (3,4, 44); r₀ - радиус диска, т.е. его размер по ободу;  - частота вращения диска; Vоб – линейная скорость вращения диска.

Примечание: В дальнейшем, при проектировании генераторов статического сверхсильного магнитного поля (ССМП), например, с целью оптимизации их размеров и характеристик, целесообразно размер ди-ска по ободу принимать кратным числу 1,68, которое выражает так называемую "золотую" пропорцию [43], а также векторную диаграмму тока в лайнере (рис.4.5)

Для оценок характеристик генератора ССМП - радиус диска 0,8 м, а толщину 1,68 мм (см. рис.4.4).

Начальные условия: между электронами и кристаллической решеткой нет взаимодействия, то движения решетки диска не передавалось бы электронам (е-газу), средняя скорость которых оставалась бы равной нулю, а их средняя скорость "U" относительно решетки была бы равна "V" - линейной скорости враще-ния диска, то плотность тока, в ободе диска, определяется формулой:

(4.40)

и обусловлена не движением электронов, а движением положительных зарядов в узлах решетки со скоростью вращения диска V. А это, вообще говоря по определению [22] - чистый конвекционный ток, который должен генерировать ССМП в соответствии с законом Био-Савара-Лапласа.

Уравнение движения электронов в этом случае имеет вид:

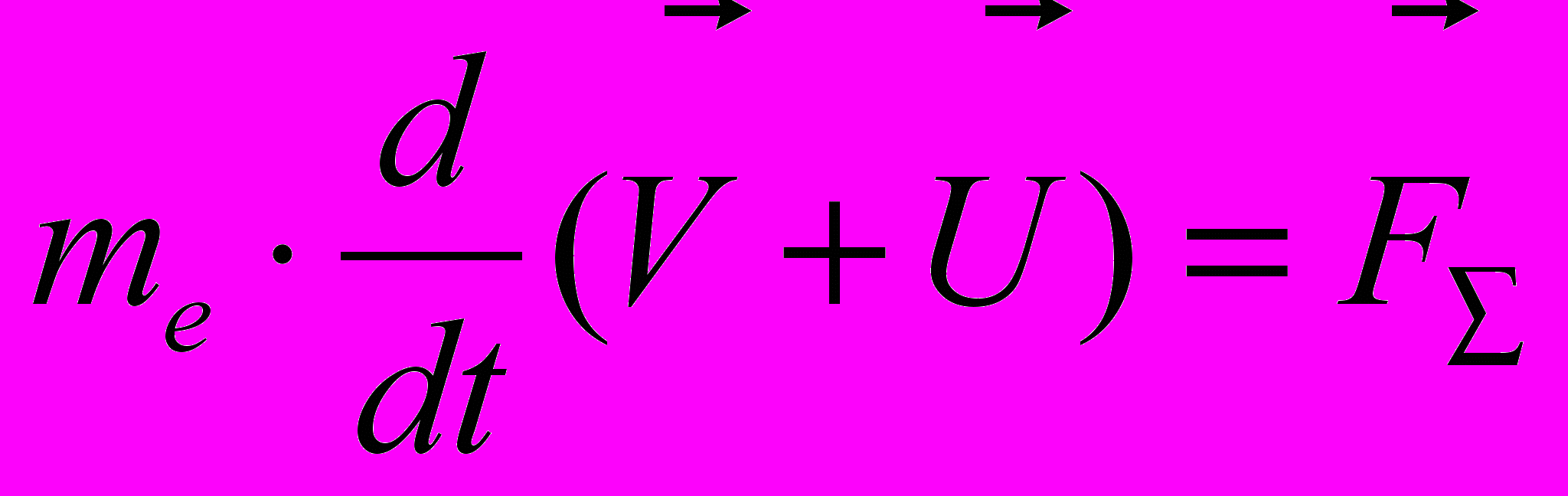, (4.41)

где: – полная скорость электронов; 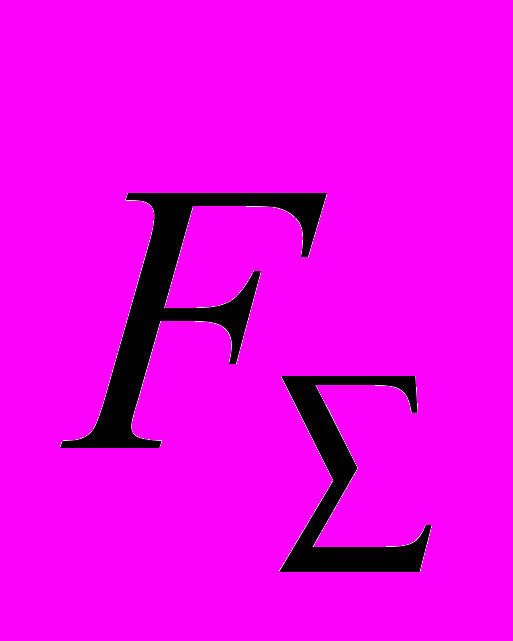– равнодействующая сила действующая на каждый электрон е-газа.

Сила в (4.41) слагается из силы трения между электронами и ионами решетки ( R₁), а также силы их взаимодействия (и магнитного) между собой в е-газе (R₂). В конце концов сила (4.41) определяется электрическим сопротивлением материала диска-лайнера и ЭДС индукции, препятствующей изме-нению силы тока в диске от сил инерции. ЭДС индукции характеризуется коэффициентом самоин-дукции - L. Понятно, что инертность электрического тока в ободе диска обусловлена не только массой электрона, но и в большей степени магнитным их взаимодействием между собой, а также силой (4.31).

С учетом сказанного и (4. 32) уравнение (4.41) можно записать в виде:

(4.42)

Отличие уравнения (4.42) от (4.41) заключается в том,что к силе F(u) добавляются силы инерции, как это требуют общие положения механики относительного движения.

Теперь вместо того, чтобы разыскивать вид функции F(u), как это обычно делают, для решения нашей задачи мы можем просто воспользоваться уравнением переменных токов [44,c.193-194]:

(4.43)

Так как мы раскручиваем наш диск - лайнер с ускорением от достаточно мощного внешнего привода и используем специальный технологический прием, существенно снижающий ЭДС индукции.

Предельно величина плотности тока для любого неохлажденного проводника равна 10⁷А/м [3,4,27,28] мы можем легко определить частоту вращения диска, при которой она достигнет этого значения. По (4.47) она получается равной 480000 об/мин.

Такой частоте вращения диска-лайнера соответствует величина напряженности ССМП равная ≈ 10 ТА/м с индукцией равной 10 МТл, почти как у звезды типа БК [46].

Здесь необходимо отметить, что значение характеристик ССМП получены без учета эффекта сепарации е-газа в скин-слое обода диска-лайнера, который ведет к значительному росту концентрации электронов в скин-слое, а следовательно и плотности тока в (4.48). Не будь эффекта ДСП - лайнер-диск мгновенно бы испарился. Отсюда и поправки на целый порядок частоты вращения. Целый ряд технологических «ухищрений» привели к вполне «рабочей» частоте вращения диска, порядка 5 – 7 тыс об/мин.

Чтобы хотя бы качественно оценить в первом приближении влияние эффекта сепарации е-газа в скин-слое раскручиваемого диска на величину генерируемой индукции ССМП, нам необходимо определить зависимость концентрации электронов в е-газе скин слоя от частоты вращения диска-лайнера. Это необходимо еще и для того, чтобы случайно не достичь при раскрутке диска линейной скорости вращения обода диска в 10 км/с, при которой он просто расплавится и испарится [46, c.128], то есть перестанет существовать для экспериментатора как объект исследования, создав иллюзию мгновенного исчезновения.

Для решения этой архиважной задачи мы воспользуемся не безызвестным в науке локальным принципом эквивалентности [12,22]. Дело в том, что в соответствии с ним допускается сравнение (количественная оценка) полей гравитационных и центробежных сил только в объеме рассматривае-мого тела. Но при этом надо твердо помнить, что поля центробежных сил действуют только в объеме сравниваемого тела в то время как гравитационные - действуют и за внешней физической поверхностью тела, то есть в окружающей его среде. Тогда можно принять, что ближайшей, известной формулой аналогом, по которой можно оценить изменение концентрации электронов в е-газе скин слоя быстро вращающегося диска может послужить так называемая "барометрическая формула" Больцмана [26].

Данную функциональную зависимость достаточно просто проверить и эксперимен-тально, используя быстро вращающийся диск и магнитометр.

Из (4.52) следует, что чем больше радиус диска и чем ниже его температура тем ниже и критическая частота вращения лайнера, приводящая к реализации эффекта ДСП. Здесь нужна оптимизация этих параметров по критерию, которая даст возможность резко снизить как энергию затрачиваемую на раскрутку лайнера, так и спроектировать летательный аппарат со сверхнизкими удельными харак-теристиками.

Следует отметить некоторые «неординарные», на первый взгляд, свойства диска-лайнера.

Первое - это кажущаяся невероятной раскрутка диска-лайнера из неферромагнитного материала до частот вращения в несколько десятков кГц, а иногда и более, что с классических позиций теории сопротивления материалов [49] вроде бы невозможно из-за его разрушения от действия огромных по величине центробежных сил. Однако, это не так, как показали эксперименты. Дело в том, что если в балансе сил, действующих на материал диска-лайнера, учесть эффект сепарации е-газа в скин слое, т. е. разделение электрических зарядов между ободом и валом диска, то появившаяся кулоновская сила приводит в расчетах и экспериментах к весьма любопытному результату. Диск в принципе не может разрушиться под действием центробежных сил, поскольку кулоновская сила, существенно больше центробежных. В эксперименте, материал диска работает не на растяжение, а на сжатие.

Визуально это проявляется в том, что раскручиваемый диск-лайнер всегда деформировался в "чашу" или "блюдце". В конце эксперимента форма диска-лайнера восстанавливается до исходной.

Второе - при частотах близких к критической нормальный скин-эффект, как правило, трансформиру-ется в аномальный [44, 48], т. е. вышедший из материала обода диска коротко замкнутый кольцевой дуговой разряд, или короткозамкнутый тороидальный электронный жгут (вихрь) КОРТЭЖ.


В этой части книги мы говорили о принципиальных вещах и оценке качества - подобия процессов происходящих в ЕПТ, следующая часть книги будет посвящена полностью созданию образа или визуализованной модели атома водорода, как главного Вселенского РАстворителя и СОтворителя.


Л И Т Е Р А Т У Р А

1. Агафонов К.П. Трение - относительность - кванты, или универсальная модель взаимодействий. М., ВНИИТ ЭИР, 1990.

4. Калашников С.Г. Электричество. М., Наука. 1985.

6. Гинзбург В.Л. Некоторые проблемы физики и астрофизики. В кн.: Физика сегодня и завтра. Под ред. академика В.М. Тучкевича. Л., Наука. 1973, с.5-70.

7. Барашенков В.С., Юрьев М.З. О новых теориях вакуума. Физическая мысль России. №1-1995, с.32-40.

8. Авраменко Р.Ф. и др. Энергетика будущего - альтернативный подход. М., ИТАР-ТАСС, Аномалия. №1(23)-1994, с.34-36.

11. Шкловский И.С. Звезды: их рождение, жизнь и смерть. М., Наука. 1984.

12. Иванов Б.Н. Законы физики. М., Высшая школа. 1986, с.294.

16. Имянитов И.М. Тропинка в атмосфере. Л., Гидрометеоиздат, 1982.

18. Игнатов Б.Н. Естественно-научная модель шаровой молнии. Оборонная техника. М., НТЦ "Информатика", №1-2 1996, с.47-52.

22. Яворский Б.М., Детлаф А.А. Справочник по физике. М., Ф-М. Л. 1963.

23. Хазен А.М. О возможном и невозможном в науке. М., Наука.1988.

24. Чернин А.Д. Звезды и физика. М., Наука. 1984.

25. 26. Кикоин И.К., Кикоин А.К. Молекулярная физика. М.,Ф-М. Л. 1963.

27. Бертинов А.И., Бут Д.А. Вопросы проектирования линейных магнитогидродинамических генераторов постоянного тока. М., МАИ. 1966.

28. Богородицкий Н.П., Пасынков В.В., Тареев Б.М. Электротехнические материалы. Л., Энергия.1977.

29. Гольдин Л.Л. Физика ускорителей. М., Наука. 1983.

41. Баланин Р. Ловитель гравитационных волн. Техника-молодежи. №9-1991, с.6-9.

42.Марголин А.Л. Власть всемирного тяготения. М., Известия 12.03.1999.

44. Тамм И.Е. Основы теории электричества. Наука. 1976, с.189-193.

46. Карцев В.П. Магнит за три тысячелетия. М., Энергоатомиздат. 1988.

47. Бережной А.Б., Игнатов Б.Н. Способ получения статического сверхсильного магнитного поля. Заявка на патент РФ N 2001119318/09 от 13.07.2001.

48. Бережной А.Б. Инженерно-физическое обоснование способа получения неограниченного количества энергии. Сборник "Духовная Россия и интернет".М.,Социум. 2002, с.104-107.


А.Б. Бережной Москва 2008.

4