Рабочая учебная программа по курсу по выбору «Планарные графы» Для Проп по направлению «050100 Педагогическое образование»
| Вид материала | Рабочая учебная программа |
- Рабочая учебная программа по курсу по выбору «Многочлены от нескольких переменных», 166.1kb.
- Рабочая учебная программа по курсу по выбору «Линейные операторы в евклидовых пространствах», 175.66kb.
- Рабочая учебная программа по курсу по выбору «Алгебры с делением над полем действительных, 179.95kb.
- Рабочая учебная программа по дисциплине «Методика обобщающего повторения» для Проп, 154.14kb.
- Рабочая программа учебная дисциплина Историография истории России Направление подготовки, 227.18kb.
- Рабочая программа учебно-педагогической практики (летние лагерные сборы) на 2010-2011, 438.34kb.
- Рабочая программа учебно-исследовательской практики на 2011-2012 учебный год Направление, 225.84kb.
- Рабочая учебная программа по дисциплине по выбору студентов «Математическое моделирование, 228.62kb.
- Рабочая программа учебно-полевой практики по зоологии 2010-2011 учебный год, 254.69kb.
- Программа вступительного экзамена в магистратуру по направлению подготовки: 050100., 85.55kb.
Министерство образования и науки Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
«Уральский государственный педагогический университет»
Математический факультет
Кафедра алгебры и теории чисел
РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА
по курсу по выбору «Планарные графы»
Для ПрОП по направлению «050100 – Педагогическое образование»,
профиль «Математика»
по циклу Б3 – профессиональный цикл
-
Очная форма обучения
Курс – 4
Семестр – 8
Объём в часах всего – 86
в т. ч.: лекции – 10
практические занятия – 20
лабораторные занятия – 0
самостоятельная работа – 56
Зачет – 8 семестр
Екатеринбург 2011
Рабочая учебная программа по курсу по выбору «Планарные графы» ГОУ ВПО «Уральский государственный педагогический университет» Екатеринбург, 2011. – 11 с.
Составитель:
Мурзинова Г.С., , к.ф.-м.н., доцент, математический факультет
Рабочая учебная программа обсуждена на заседании кафедры алгебры и теории чисел УрГПУ (Протокол № 9 от 05.05.2011).
Зав. кафедрой С.С. Коробков
Председатель методической комиссии И.Н. Семенова
Декан математического факультета В.П. Толстопятов
- ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
В связи со стремительным внедрением компьютерной техники во все сферы человеческой жизни в течении последних десятилетий наблюдается бурное развитие теории графов. Идеи и методы теории графов глубоко проникли в такие области знания, как информатика, физика, химия, биология, статистика, экономика, лингвистика, психология и др.
- Цели и задачи курса
Цели изучения курса::
- сформировать у студентов представление об основных разделах дискретной математики;
Задачи изучения курса
- создать теоретико – множественный фундамент курса;
- определить основные элементы математического языка;
- познакомить студентов с комбинаторными методами рассуждений;
- представить несколько важных разделов теории графов;
1.2. Место дисциплины в структуре ПрОП
Данный курс изучается в рамках вариативной части профессионального цикла. Его изучение основывается на таких общематематических понятиях, как множество, отображение, функция. Курс базируется на дисциплине «Дискретная математика», поэтому необходимо знать основные понятия теории графов. Данный курс тесно связан с алгеброй, геометрией и информатикой. Из курса геометрии используется Теорема Эйлера о многогранниках, а из курса алгебры – понятие разбиения множества. Курс имеет важное методологическое значение как для формирования общего представления о математике, так и для решения конкретных математических задач при осуществлении профессиональной деятельности бакалавров.
1.3. Требования к результатам освоения дисциплины:
Процесс изучения дисциплины направлен на формирование следующей профессиональной компетенции:
способен демонстрировать, применять, критически оценивать и пополнять математические знания,
а также части профессиональной компетенции:
готов организовывать различные виды учебно-исследовательской и проектной деятельности обучающихся.
Основные требования к результатам освоения дисциплины представлены в следующей таблице в виде признаков сформированности компетенции. Требования формулируются по двум уровням: пороговый и повышенный и в соответствии со структурой, принятой в ФГОС ВПО: знать, уметь, владеть.
| Уровни сформированности компетенции | Структура компетенции | Основные признаки уровня | |
| Пороговый уровень | Знает основы планарных графов и раскраски графов | Формирует определения планарных графов, гамильтоновых графов, паросочетания. | |
| Воспроизводит основные идеи, которые используются при доказательстве теорем о планарных графах, двудольных графах и ориентированных графах. | |||
| Приводит основные определения: планарного графа, хроматического числа, гамильтонова графа, ориентированного графа. | |||
| Понимает связи между различными типами графов. | |||
| Умеет доказывать утверждения | Умеет аргументировано обосновывать основные положения курса. | ||
| Демонстрирует доказательства теорем и объясняет их ход. | |||
| Умеет решать задачи по курсу «Планарные графы». | Знает основные методы решения типовых задач и умеет их применять на практике. | ||
| Аргументирует выбор решения задачи и составляет соответствующий ему план решения. | |||
| Оценивает достоверность полученного решения задачи. | |||
| Владеет профессиональным языком теории графов. | Владеет терминологией теории графов. | ||
| Способен корректно представить знания в математической форме. | |||
| Владеет разными способами представления информации из теории графов (аналитическим, графическим, символическим и др.) | |||
| Интерпретирует знания, полученные при изучении курса примерами из своей будущей профессиональной деятельности. | |||
| Повышенный уровень | Знает основы курса «Планарные графы». | Знает роль понятия графа в математике. | |
| Устанавливает связи между основными идеями теории графов и другими математическими теориями, дисциплинами и т.д. | |||
| Понимает сущность и важность основных типов графов. | |||
| Умеет доказывать утверждения данного курса. | Понимает границы использования методов теории графов. | ||
| Выделяет главные смысловые аспекты в доказательстве утверждений теории графов. | |||
| Понимает специфику требований, предъявляемых к доказательствам в теории графов. | |||
| Умеет решать задачи по данному курсу. | Применяет методы теории графов в незнакомых ситуациях. | ||
| Оценивает различные методы решения задачи и выбирает оптимальный. | |||
| Владеет профессиональным языком теории графов. | Корректно переводит информацию с одного математического языка на другой. | ||
| Критически осмысливает полученные знания. | |||
| Способен проявить свою компетентность в теории графов в различных ситуациях. | |||
| Способен передавать результат проведенных исследований в виде конкретных рекомендаций в терминах теории графов. | |||
| | | ||
Таблица № 2
| Уровни сформированности компетенции | Структура части компетенции | Основные признаки уровня |
| Пороговый уровень (как обязательный для всех студентов-выпускников вуза по завершению освоения дисциплины) | Знает этапы исследования. | Знает основные задачи исследовательского типа в дисциплине «Планарные графы». |
| Знает, какие типы задач школьного курса математики имеют связи с теорией графов. | ||
| Может разработать исследовательские задания на материале школьного курса математики. | Может предложить конкретные задачи исследовательского характера, связанные с теорией графов и доступные для учащихся. | |
| Может поставить вопросы, составить план решения предложенных задач. | ||
| Может организовать локальную исследовательскую деятельность учащихся. | Может сформулировать цель, гипотезу, предложить пути решения задачи. | |
| Способен оценить полученные результаты и наметить пути дальнейшего исследования. | ||
| Повышенный уровень | Знает основные требования, предъявляемые к проектам. | Знает темы, связанные с планарными графами, и подходящие для разработки исследовательских проектов со школьниками. |
| Умеет выбрать тему исследовательского проекта. | Может сформулировать цель, гипотезу, объект и предмет исследовательского проекта. | |
| Владеет основами организации работы над проектом. | Способен организовать исследовательскую деятельность группы участников по выбранной теме проекта. |
1.4. Объем дисциплины и виды учебной работы
Согласно учебному плану курс «Планарные графы» на очном отделении изучается бакалаврами на 4 курсе в 8 семестре, форма контроля – зачет. На изучение курса отводится 60 учебных часов, в т.ч. 30 уч.ч. аудиторных занятий и 30 уч.ч. самостоятельной работы студентов. Аудиторные занятия включают 10 уч.ч. лекций, 20 уч.ч. практических занятий. Предусматривается выполнение двух контрольных работ в соответствии с графиком проведения контрольных мероприятий. Контроль и организация самостоятельной работы осуществляется с помощью домашних заданий.
На заочном отделении дисциплина «Планарные графы» изучается на 4 курсе в 8 семестре (отчетность в 8 семестре в форме зачета). На изучение курса отводится также 60 учебных часа, в т.ч. 18 уч.ч. аудиторных занятий и 42 уч.ч. самостоятельной работы студентов. Аудиторные занятия включают 6 уч.ч. лекций, и 12 уч.ч. практических занятий. Предусматривается выполнение одной контрольной работы.
Общая трудоемкость дисциплины составляет две зачетные единицы.
-
УЧЕБНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
2.1. Учебно-тематический план очной формы обучения
| № п./п | Наименование раздела, темы | Всего тру- доем- кость | Аудиторные занятия | Самостоя- тель- ная работа | |||
| Все- го | Лек- ции | Пра- кти- чес- кие | Ла- бора- тор- ные | ||||
| 1 | Планарные графы | 20 | 8 | 4 | 4 | | 12 |
| 2 | Гамильтоновы графы | 14 | 4 | 2 | 2 | | 10 |
| 3 | Раскраска графа | 22 | 8 | 4 | 4 | | 14 |
| 4 | Двудольные графы и паросочетания | 14 | 4 | | 4 | | 10 |
| 5 | Ориентированные графы | 16 | 5 | | 6 | | 11 |
| | ИТОГО: | 86 | 30 | 10 | 20 | | 56 |
- СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
3. 1. Структурированное содержание дисциплины
| № п/п | Наименование раздела (темы) | Содержание раздела |
| 1 | Планарные графы | Планарные графы. Теорема Эйлера о многогранниках. Непланарность графов 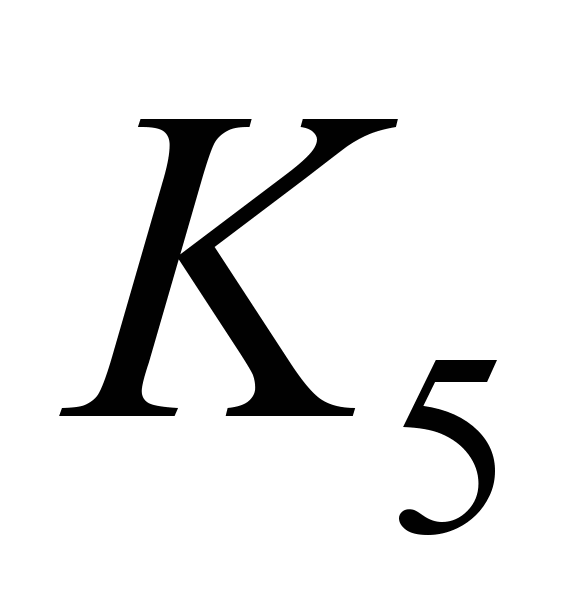 и и 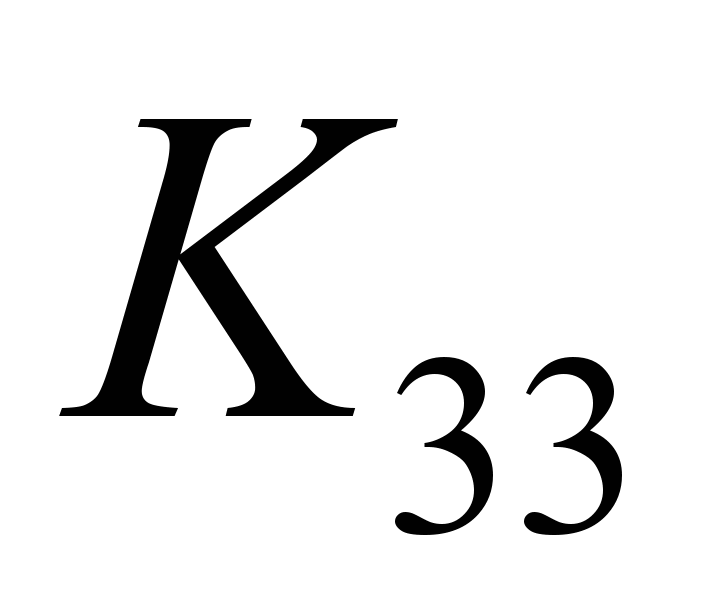 . Критерий планарности графа. Задача о трех кольцах. . Критерий планарности графа. Задача о трех кольцах. |
| 2 | Гамильтоновы графы | Гамильтоновы графы. Необходимое условие гамильтоновости графа. Достаточное условие гамильтоновости графа. (Теорема Дирака). |
| 3 | Раскраска графа | Задачи, приводящие к поиску хроматического числа. Проблема четырех красокю Теорема: Хроматисеское число планарного графа не превосходит пяти. |
| 4 | Двудольные графы и паросочетания | Критерий двудольности графа. Паросочетания. Теорема Холла о свадьбах. Задача о назначении. |
| 5 | Ориентированные графы | Орграфы. Сильная связность. Эйлеровы и гамильтоновы орциклы. Сети. Расстояние в сетях. |
3. 2. Перечень тем лекционных занятий
На очном отделении:
Лекция № 1. Планарные графы. Теорема Эйлера о многоугольниках.
Лекция № 2. Критерий планарности графа. Задача о трех колодцах.
Лекция № 3. Гамильтоновы графы.
Лекция № 4. Хроматическое число планарного графа. Задачи, приводящие к поиску хроматического числа.
Лекция № 5. Раскраска графа. Проблема четырех красок.
На заочном отделении:
Лекция № 1. Планарные графы.
Лекция № 2. Раскраска графов.
Лекция № 3. Ориентированные графы.
3. 3. Перечень тем практических занятий
На очном отделении:
Занятие № 1. Планарные графы.
Занятие № 2. Критерий планарности графа.
Занятие № 3. Гамильтоновы графы.
Занятие № 4. Хроматическое число планарного графа.
Занятие № 5. Раскраска графа.
Занятие № 6. Двудольные графы. Критерий двудольности.
Занятие № 7. Паросочетания.
Занятие № 8. Ориентированные графы.
Занятие № 9. Эйлеровы и гамильтоновы графы.
Занятие № 10. Сети. Расстояние в сетях.
На заочном отделении:
Занятие № 1. Планарные графы.
Занятие № 2. Раскраска графов.
Занятие № 3. Ориентированные графы.
Занятие № 4. Двудольные графы.
Занятие № 5. Двудольные графы.
Занятие № 6. Гамильтоновы графы.
3. 4. Перечень тем лабораторных работ
Согласно учебному плану выполнение лабораторных работ по данному курсу не
предусмотрено.
3.5. Перечень тем занятий, реализуемых в активной и интерактивной формах
Каждая лекция содержит в себе интерактивные фазы проведения занятия. Все практические занятия проводятся в интерактивной форме, начиная с анализа условия задач до обсуждения вариантов решения.
- САМОСТОЯТЕЛЬНАЯ РАБОТА И ОРГАНИЗАЦИЯ КОНТРОЛЬНО-ОЦЕНОЧНОЙ ДЕЯТЕЛЬНОСТИ
4.1. Темы, вынесенные на самостоятельное изучение для студентов очной и заочной форм обучения
- Задачи об оптимальном назначении.
- Задачи о составлении расписания.
- Потоки в сетях. Алгоритм Форда – Фалкерсона.
4.2. Темы контрольных работ для студентов очной и заочной форм обучения
- Планарные графы.
- Двудольные графы.
4.3. Примерные темы курсовых работ
- Двудольные графы и паросочетания.
- Потоки в сетях.
- Изоморфизм графов.
4. 4. Вопросы для подготовки к зачету
- Планарные графы.
- Теорема Эйлера о многогранниках.
- Критерий планарности графа.
- Гамильтоновы графы.
- Необходимое условие гамильтоновости графа.
- Достаточное условие гамильтоновости графа.
- Хроматическое число.
- Проблема четырех красок.
- Критерий двудольности графа.
- Паросочетания.
- Теорема Холла о свадьбах.
- Задача о назначении.
- Оргафы.
- Сильная связность.
- Эйлеровы и гамильтоновы графы.
- Расстояние в сетях.
4. 5. Типы задач для подготовки к практической части зачета
- Задачи на планарные графы.
- Задачи на гамильтоновы графы.
- Задачи на раскраску графа.
- Задачи на двудольные графы и паросочетания.
- Задачи на орграфы.
5. УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОМАЦИОННОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
5.1. Рекомендуемая литература
Основная
- Андерсон Д.А. Дискретная математика и комбинаторика. / пер. с англ. М.М, Беловой; под ред. Шкильняка С.С. и Саит-Аметова М.Р. М.: Изд. дом «Вильямс», 2003. 960с
- Виленкин Н.Я. Индукция. Комбинаторика: пособие для учителей / М.: Просвещение, 1976. – 48 c.
- Виленкин Н.Я. Комбинаторика М.: Физматгиз, 1969. 328с.
- Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по курсу дискретной математики, учеб. пособие для вузов по спец. «Прикладная математика» - М.: Наука, 1977. 368с.
- Гончарова Г.А. Элементы дискретной математики, учеб. пособие для студентов учреждений сред. проф. образования по спец. информатики и вычислит. техники М.: ФОРУМ: ИНФРА, 2004. 268с.
- Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. Лекции по теории графов М.: Наука, 1990. 268с.
- Матросов В.Л. , Стеценко В.А. Лекции по дискретной математике: учеб. пособие для магистрантов мат. фак. пед. ун-тов, М.: Прометей, 1997. 220с.
- Уилсон Р. Введение в теорию графов, пер. с англ. Никитиной И.Г., под. ред. Гаврилова Г.П. М.: Мир, 1977. 208с.
Дополнительная
- Горбатов, В.А. Основы дискретной математики, учеб. пособие для вузов М.: Высш. шк., 1986. – 312с.
- Ежов И.И., Скороход А.В., Ядренко М.И. Элементы комбинаторики М.: Наука, 1977. 80с.
- Замятин А.П. Графы и сети, учеб. пособие, Урал. гос. ун-т. Екатеринбург: Изд.-во Урал. ун-та, 2004. 160с.
- Кузьмин О.В. Перечислительная комбинаторика: учеб. пособие для студентов вузов М.: Дрофа, 2005. 110с.
- Москивина Г.И. Дискретная математика М.: Логос, 2004. 240с.
- Мурзинова Г.С. Дискретная математика, учеб. пособие УрГПУ, Екатеринбург, 2008, 103 с.
- Яблонский С.В. Введение в дискретную математику, учеб. пособие для вузов, под ред. Садовничего В.А. 3-е изд. М.: Высш. шк., 2001. 384с.
5.2. Информационное обеспечение дисциплины
При изучении данной дисциплины рекомендуется использовать:
- Электронный оптический диск (CD-ROM), подготовленный для студентов математического факультета с учебными и методическими материалами по дисциплинам кафедры алгебры и теории чисел.
- Цифровые образовательные ресурсы сети Интернет
6. МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ И ДИДАКТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
При изучении дисциплины «Планарные графы» рекомендуется использовать технические средства обучения (персональные компьютеры, медиа проектор).
7. СВЕДЕНИЯ ОБ АВТОРЕ ПРОГРАММЫ
Мурзинова Галина Сергеевна,
к.ф.-м.н.,
доцент каф. алгебры и теории чисел УрГПУ
Рабочий телефон: (343) 371-45-97
РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА
по курсу по выбору «Машины с неограниченными регистрами»
Для ПрОП по направлению «050100 – Педагогическое образование»,
профиль «Математика»
по циклу Б3 – профессиональный цикл
Подписано в печать Формат 60х84/16
Бумага для множительных аппаратов. Усл. печ. л.
Тираж экз. Заказ
Уральский государственный педагогический университет.
620017 Екатеринбург, пр. Космонавтов, 26.
