Урок информатики в 10 классе. Раздел «Логика»

Вид материала

Занятие

Содержание План урока. Для этого класс разделить на две команды (каждой команде отводится 10 минут) Логическое умножение  КОНЪЮНКЦИЯ Логическое сложение – ДИЗЪЮНКЦИЯ Логическое отрицание : ИНВЕРСИЯ Неверно, что Логическое следование:  ИМПЛИКАЦИЯ Логическая равнозначность: ЭКВИВАЛЕНТНОСТЬ 5. Закрепление изученного П—«пасмурная погода» ; Д

Подобный материал:

• Урок на тему «Решение логических задач с помощью электронных таблиц ms excel\ Раздел, 149.53kb.
• Урок. Математика 6 класс. «Длина окружности», 95.5kb.
• Евграфова Наиля Минифаиловна, учитель информатики моусош №2, рб, Альшеевский район,, 287.72kb.
• Самостоятельная работа из 4 вариантов (см. Приложение 3). Структура парного урока, 102.7kb.
• Урок информатики в 7 классе «Векторные графические редакторы», 122.13kb.
• Программа курса и темы практических занятий; Логика в таблицах и схемах. Логика как, 1722.34kb.
• Фирсова Наталия Анатольевна, учитель физики и информатики моу сош №27 урок, 123.18kb.
• Конструирование из мозаики, 71.13kb.
• Логика в образовании, 153.37kb.
• Активизация процесса обучения через приемы занимательности на уроках информатики. Обобщающий, 63.82kb.

Урок информатики в 10 классе. Раздел «Логика».

Составила учитель информатики Больше-Кайбицкой СОШ Долматова Н. А.

Тема: «Логические схемы и логические выражения»

Цели урока:

1. Образовательные

• Получить представление об алгебре высказываний.

• Построение таблиц истинности сложных высказываний.
  
• Логические схемы и логические выражения.
  
• Решение логических задач.
  

2. Развивающие

• Развитие исследовательской и познавательной деятельности.
  
• Лаконично, полно и содержательно отвечать и делать обобщающие выводы.
  

3. Воспитательные

• Формирование аккуратности при работе с компьютером.
  
• Понимание связей между другими учащимися, культурой поведения.
  

Тип урока: комбинированный


Методы организации учебной деятельности:

• фронтальная,
  
• индивидуальная,
  
• групповая,
  
• ученик-учитель,
  
• ученик-транспарант.
  

Продолжительность занятия: 2 академических часа.

Оборудование и ТСО

• Мультимедиапректор
  
• Карточки, карточки-помощники
  
• Компьютеры
  
• Слайды
  

ПЛАН УРОКА.

1. Информационная минутка. Отводится 5-7 минут на обсуждение компьютерных новостей из прессы.
   

Информационная минутка — это обоснованный повод привлечь школьников к самостоятельному чтению (оценке) прессы. Эти качества необходимы юным членам информационного общества и для наглядности эти материалы проектируются на экране мультимедиа.

2. Обобщение по материалу предыдущих уроков построить в виде фронтальной беседы, индивидуальной и групповой работы с учащимися класса, в ходе которой повторить основные понятия информатики, системы счисления, логические выражения, логические операции.
   

Для этого класс разделить на две команды (каждой команде отводится 10 минут):

• Первая команда составляет таблицы истинности для логических высказываний.
  

а) А или В и не С

б) (А или не В) и (не А и не В)

• Вторая команда отвечает на вопросы, задаваемые учителем(предварительно подготовившись)
  

Предлагаемые вопросы:

• Что такое системы счисления, группы систем счисления?
  
• Что такое высказывание? Какие виды высказываний Вы знаете (Привести примеры общих, частных и единичных высказываний).
  
• Какие логические операции Вы знаете?
  
• Приоритетность выполнения логических операций.
  

3. Подвести итог опроса команд.
   
4. Изучение нового материала.
   

Раздать карточки-помощники пяти основных логических операций на проекторе вспомнить правила каждого.

Логические операции и таблицы истинности

A	B	F
1	1	1
1	0	0
0	1	0
0	0	0

F = A & B.

Логическое умножение  КОНЪЮНКЦИЯ  - это новое  сложное выражение будет истинным только тогда, когда истинны оба исходных простых выражения. Конъюнкция определяет соединение двух логических выражений с помощью союза И.

 

 

A	B	F
1	1	1
1	0	1
0	1	1
0	0	0

F = A + B 

Логическое сложение – ДИЗЪЮНКЦИЯ - это новое сложное выражение будет истинным тогда и только тогда, когда  истинно хотя бы одно из исходных (простых) выражений. Дизъюнкция определяет соединение двух логических выражений с помощью союза ИЛИ

 

A	неА
1	1
1	0

Логическое отрицание : ИНВЕРСИЯ - если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным/ Данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО

 

 

A	B	F
1	1	1
1	0	0
0	1	1
0	0	1

Логическое следование:  ИМПЛИКАЦИЯ - связывает два простых логических выражения, из которых первое является условием (А), а второе (В)– следствием из этого условия. Результатом ИМПЛИКАЦИИ является ЛОЖЬ только тогда, когда условие А истинно, а следствие В ложно. Обозначается символом  "следовательно"  и  выражается словами ЕСЛИ … , ТО …

 

 

A	B	F
1	1	1
1	0	0
0	1	0
0	0	1

Логическая равнозначность: ЭКВИВАЛЕНТНОСТЬ - определяет результат сравнения двух простых логических выражений А и В. Результатом ЭКВИВАЛЕНТНОСТИ является новое логическое выражение, которое будет истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. Обозначается символом "эквивалентности"

 

 


Удобным способом представления логических выражений являются логические схемы. Цифры в начале входящих стрелок — логические операнды; цифры в конце выходящих стрелок — результаты операций.. Работа интегральных схем на компьютерах основана на логических операциях.


5. Закрепление изученного


Разобрать логические схемы и записать функции, описывающие состояние логических схем


Пример 1.


или

и

не


А


не

В


С


Пример 2.

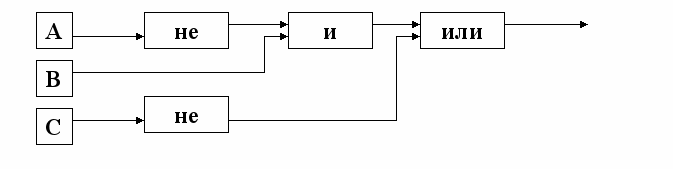
5. Формирование практических навыков.
   

Пример 1. Построить логические схемы по логическому выражению при любых значениях Х:

1. х₁ и (не х₂ или х₃ )
   
2. х₄ и (х₁ и х₂ и х₃ или не х₂ и не х₃ )
   

Пример 2. Дана логическая схема. Построить логическое выражение, соответствующее этой схеме. Вычислить значения выражения для

1. х₁ =0, х₂ =1
   
2. х₁ =1, х₂ =0
   
3. х₁ =1, х₂ =1
   
4. х
   
   
   и
   
   или
   ₁ =0, х₂ =0
   

не


и










не







Пример 3. Переведите к виду логической формулы высказывание: «Неверно,

что если погода пасмурная, то дождь идет тогда и только тогда, когда нет

ветра»

Решение. Определим следующие простые высказывания:

П—«пасмурная погода» ;

Д—«идет дождь» ;

В—«дует ветер».

Тогда соответствующее логическое выражение запишется так.

_______________

П (Д В).


6. Резюме.

Логические схемы — это та же таблица истинности, только представленная в форме логических схем. В такой форме удобно изображать цепочки логических операций и производить их вычисления.

11.Домашнее задание.

Составить логическую схему и таблицу истинности для логической функции

F=(A and B) or not (B or C),

если A=true, B=false, C=true.