Geum.ru

Самостоятельная работа из 4 вариантов (см. Приложение 3). Структура парного урока

Вид материалаСамостоятельная работа

Содержание


Алгебра логики
Логическая формула
Это сделал Коля или Саша. Но Саша этого не делал, так как в это время сдавал мне зачет. Следовательно это сделал Коля.
Это сделал Коля или Саша. Но Саша этого не делал, так как в это время сдавал мне зачет. Следовательно это сделал Коля.
Подобный материал:
Приложение 2


Урок информатики в 10 классе (2 часа) Учитель: Соломенина Вера Сергеевна, учитель информатики МОУ лицея № 102 г. Челябинска


Тема: «Операции над суждениями»

Цели:

обучающая – познакомить учащихся с основными операциями над суждениями;

развивающая – формирование логического мышления;

воспитательная – воспитание информационной культуры.

Оборудование и дидактические материалы:

девять рабочих станций с тренировочным упражнением, подготовленным в приложении MS Excel;

проектор;

доска;

презентация из 25 слайдов по теме (см. Приложение1)

Историческая справка на стенд (см. Приложение 2)

самостоятельная работа из 4 вариантов (см. Приложение 3).

Структура парного урока:
  1. Встраивание в систему уже освоенных знаний (5 мин).
  2. Создание мотивации (2 мин).
  3. Ознакомление с новым материалом (15 мин).
  4. Зарядка (2 мин).
  5. Ознакомление с новым материалом (20 мин).
  6. Зарядка (2 мин).
  7. Закрепление с выработкой умений применять изученный материал (32 мин).
  8. Подготовка к изучению нового материала (2 мин).

Содержание урока

Учитель
Доска
Тетрадь
Ученик
ПК
  1. Встраивание в систему уже освоенных знаний

Здравствуйте! Вспомним, чем занимались на прошлом уроке?

Слайд 1



Начали изучать тему «Логика».



Какой раздел логики нас особо интересует?



Алгебра логики



Что изучает алгебра логики? Кто считается основателем алгебры логики?



Высказывания

Д. Буль



В этом году исполняется 190 лет со дня рождения этого великого английского математика-самоучки. Булева алгебра в объединении с двоичной системой счисления легли в основу разработки цифрового электронного компьютера.

Последнее десятилетие жизни Буль использовал как педагог. У Буля было 5 дочерей. Третья, Алисия – видный математик, четвертая, Люси – первая в Англии женщина-профессор химии. Младшая, Этель Лилиан, вышла замуж за эмигранта из Польши Уилфрида Войнича и прославилась как автор романа «Овод».








  1. Создание мотивации

Мы говорим об алгебре логики. Что такое алгебра логики?

То есть алгебра логики заменяет высказывания переменными и связывает эти переменные при помощи логических операций.








Алгебра логики– раздел математики, который рассматривает высказывания со стороны их логических значений и логических операций над ними.



Ребята, можем ли мы изучать математику, не зная, что такое сложение, умножение, деление и другие операции?

Можем ли мы изучать алгебру логики, не зная логических операций? Итак, не будем тогда терять времени. Скорее записываем тему сегодняшнего занятия: Операции над суждениями.
Слайд 2
Операции над суждениями
Нет.


Нет.


  1. Ознакомление с новым материалом












1. Конъюнкция (логическое умножение) – соединение простых высказываний в составное с помощью связки «и».

Результат операции – логическое произведение

Обозначения: A·B, A&B, AÙB.

A = У меня есть деньги

B = У меня есть желание купить машину

Таблица истинности (ТИ):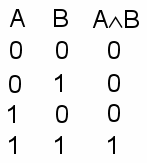




Результат И, если оба высказывания И
Слайд 3

Слайд 4
1. Конъюнкция (логическое умножение) – соединение простых высказываний в составное с помощью связки «и»

Результат операции – логическое произведение

Обозначения: A·B, A&B, AÙB.

A = У меня есть деньги

B = У меня есть желание купить машину

Таблица истинности (ТИ):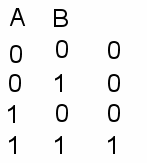


AB

Результат И, если оба высказывания И






2. Дизъюнкция (логическое сложение) – соединение простых высказываний в составное с помощью связки «или»

Результат операции – логическая сумма

Обозначения: A+B, AÚB.

A = Сегодня ко мне в гости придет Маша

B = Сегодня ко мне в гости придет Саша

Таблица истинности (ТИ):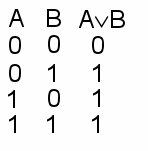



Результат И, если оба высказывания И


Мнемоническое правило:
  • В слове «конъюнкция» одна буква «и», а в слове «дизъюнкция» две буквы «и», как и в слове «или».
Слайд 5

Слайд 6

Слайд 7
2. Дизъюнкция (логическое сложение) – соединение простых высказываний в составное с помощью связки «или»

Результат операции – логическая сумма

Обозначения: A+B, AÚB.

A = Сегодня ко мне в гости придет Маша

B = Сегодня ко мне в гости придет Саша

Таблица истинности (ТИ):

Результат И, если оба высказывания И





  1. Зарядка
  1. Импликация (логическое следование) – соединение простых высказываний в составное с помощью связки
    «если - то»

Обозначение: A ® B

A = Число делится на 9

B = Число делится на 3

Таблица истинности (ТИ):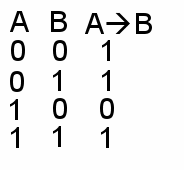



Результат Л, если предпосылка И, следствие Л
Слайд 8-9
3.Импликация (логическое следование) – соединение простых высказываний в составное с помощью связки
«если - то»

Обозначение:

A ® B

A = Число делится на 9

B = Число делится на 3

Таблица истинности (ТИ):

Р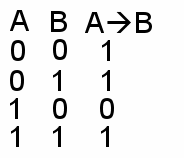езультат Л, если предпосылка И, следствие Л





  1. Эквивалентность (логическое равенство) – соединение простых высказываний в составное с помощью связки
    «тогда и только тогда, когда»

Обозначение: A ~ B, A Û B

A =Число кратно 3

B =Сумма цифр кратна 3

Таблица истинности (ТИ):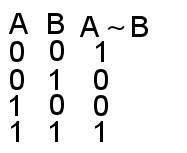



Результат И, если оба высказывания одинаковы

по истинности (весы)
Слайд 10-11
4 Эквивалентность (логическое равенство) – соединение простых высказываний в составное с помощью связки
«тогда и только тогда, когда»

Обозначение:

A ~ B, A Û B

A =Число кратно 3

B =Сумма цифр кратна 3

Т
A  B
аблица истинности (ТИ):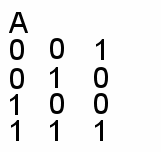


B


Результат И, если оба высказывания одинаковы

по истинности (весы)






5.Инверсия (логическое отрицание) – присоединение к простому высказыванию слов «неверно, что»

Обозначение: ¬A

Таблица истинности (ТИ):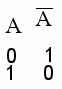



Результат И, если простое высказывание Л
  • Слово «инверсия» (от лат. Inversio - переворачивание) означает, что черное меняется на белое, зло на добро, истина на ложь, ложь на истину.
Слайд 12-14
5.Инверсия (логическое отрицание) – присоединение к простому высказыванию слов «неверно, что»

Обозначение: ¬A

Таблица истинности (ТИ):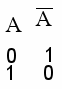



Результат И, если простое высказывание Л
  • Слово «инверсия» (от лат. Inversio - переворачивание) означает, что черное меняется на белое, зло на добро, истина на ложь, ложь на истину.






Сейчас мы имели дело с простыми высказываниями. Для таких высказываний установить истинность достаточно просто. Если несколько простых высказываний объединены в одно с помощью логических операций и скобок, то такое высказывание называется сложным.

Истинность сложного высказывания устанавливается по таблице истинности. Напишите подзаголовок:

Построение таблиц истинности сложных высказываний
Слайд 15-19
Построение таблиц истинности сложных высказываний






Логическая формула – выражение, содержащее вместо простых высказываний переменные, соединенные знаками логических операций и скобками.

Обозначается одной буквой и может принимать всего два значения: И, Л.
  • При вычислении значения логической формулы логические операции вычисляются в определенном порядке, согласно их приоритету:

Ø Ù Ú ® ~
Логическая формула – выражение, содержащее вместо простых высказываний переменные, соединенные знаками логических операций и скобками.

Обозначается одной буквой и может принимать всего два значения: И, Л.

Порядок выполнения действий:

Ø Ù Ú ® ~






Разберем на примере построение формулы сложного высказывания и определение его истинности.

Пример: В классе оказалось разбито стекло. Учитель объясняет директору: Это сделал Коля или Саша. Но Саша этого не делал, так как в это время сдавал мне зачет. Следовательно это сделал Коля. Прав ли учитель? (Построение таблицы см. Приложение 1)
Слайд 20-23
Пример: В классе оказалось разбито стекло. Учитель объясняет директору: Это сделал Коля или Саша. Но Саша этого не делал, так как в это время сдавал мне зачет. Следовательно это сделал Коля. Прав ли учитель?





  1. Закрепление с выработкой умений применять изученный материал

Сейчас работаем вместе на доске. Затем в парах тренируетесь строить ТИ в Excel.












Задание: Построить ТИ для формул:
  1. F = A Ù ØB à B
  2. F = ¬(AÚB) ~ A

Теперь вспомним Excel и поработаем с тренировочным упражнением, которое находится на диске С: и называется «Формулы». Для помощи можно взять с собой тетрадь.

Необходимо выполнить все задание на листе «Две переменные». Для тех, кто идет вперед на втором листе - дополнительное задание на оценку.

После тренировки за партами будет маленькая самостоятельная работа.

Слайд 24-25


C:\Формулы.xls



2 ученика заполняют таблицы на доске.


 В приложении Excel выполняют работу

Теперь садимся за парты. Запишем домашнее задание: Составить свою формулу, состоящую из 2 переменных и 4 операций и построить для нее таблицу истинности.






Записывают домашнее задание.



Самостоятельная работа. Я раздаю листочки. Вы их подписываете в отведенном для этого месте. И заполняете пустые клеточки. По окончании работы на обратной стороне нарисуйте смайлик, по которому я увижу, как вы поняли сегодняшний материал.






Выполняют самостоятельную работу


  1. Подготовка к изучению нового материала

Итак, ребята, с чем мы сегодня познакомились?

Какие логические операции вы узнали?

Что мы получим, если простые высказывания заменим буквами и соединим их знаками логических операций?

Хотите научиться любое сложное высказывание превращать в формулу?

Именно этим мы и займемся на следующем уроке.

В сегодня хорошо поработали. Спасибо. До встречи через неделю.






С логическими операциями.

Конъюнкцию, дизъюнкцию, импликацию, эквиваленцию, инверсию.

Логическую формулу.

Да.