«Статистические методы изучения взаимосвязей финансовых показателей деятельности» банка

Вид материала

Содержание

В абсолютном выражении
Размер прибыли, млн. руб.
Группы банков по прибыли, млн. руб.
Группы банков по прибыли, млн. руб.
Собственный капитал, млн. руб.
Аналитическая группировка
Собственный капитал, млн. руб.

Подобный материал:

1 2 3 4 5 6

Составим интервальный ряд, характеризующий распределение банков по прибыли.

Таблица 2

Интервальный ряд распределения банков по прибыли

№ группы	Группы банков по прибыли, млн. руб.	Число банков
В абсолютном выражении	В относительных единицах, %
I II III IV V	62 – 117 118 – 173 174 – 229 230 – 285 286 и выше	7 13 8 5 4	18.92 35.14 21.62 13.51 10.81
Итого	37	100

Данные группировки (табл. 2) показывают, что более 75% (75.68%) банков получают прибыль менее 230 млн. руб.

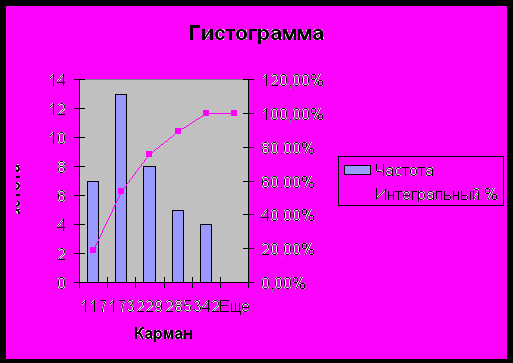
Построение графиков полученного ряда распределения (гистограммы, комуляты).

а) Гистограмма представляет собой столбчатый график, построенный по полученным данным, которые разбиваются на несколько интервалов.

Число данных, попавших в каждый из интервалов(частота) выражается высотой столбика.

Для построения гистограммы на оси абсцисс откладывают интервалы, по оси ординат – число банков(частоты).

По гистограмме находят значение моды – случайной величины, встречающейся с наибольшей вероятностью, в дискретном ряду – варианта, имеющего наибольшую частоту. Графически видно, что самая высокая точка О = 145 - это и есть мода

б) Для построения комуляты нужно рассчитать накопленные частоты. Накопленные частоты показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение и определяются последовательным суммированием частот интервала.

Таблица 3

Размер прибыли, млн. руб.	Число банков	Накопленная частота
62 – 118 118 – 174 174 – 230 230 – 286 286 - 342	7 13 8 5 4	7 20 28 33 37
Итого	37	—

При построении комуляты интервального ряда распределения нижней границе первого интервала соответствует частота, равная нулю, а верхней границе – вся частота данного интервала. Верхней границе второго интервала соответствует накопленная частота, равная сумме частот первых двух интервалов, и т. д. Медиана - значение признака, приходящееся на середину ранжированной совокупности

Медианным является интервал, которому соответствует накопленная частота, превышающая полусумму частот ряда.

Графически видно, что накопленная частота будет превышать полусумму в точке х = 202 - это и есть медиана

3) Расчет характеристики интервального ряда распределения.

а) Расчет средней арифметической.

Если значения осредняемого признака заданы в виде интервалов, т.е. интервальных рядов распределения, то при расчете средней арифметической величины в качестве значений признаков в группах принимают середины этих интервалов, в результате чего образуется дискретный ряд.

От интервального ряда перейдем к дискретному путем замены интервальных значений их средними значениями (простая средняя между верхней и нижней границами каждого интервала). При этом величины открытых интервалов условно приравниваются к интервалам, примыкающим к ним.

Таблица 4

Расчет средней арифметической в рядах распределения

Группы банков по прибыли, млн. руб.	Число банков, f	Середина интервала, x	*x f**
62 – 117 118 – 173 174 – 229 230 – 285 286 и выше	7 13 8 5 4	89.5 145.5 201.5 257.5 313.5	626.5 1891.5 1612 1287.5 1254
Итого	37	-	6671.5

Вычисление средне арифметической взвешенной из групповых средних, осуществляется по формуле:

x _ар =  x*f / f (2)

x _ар= 6671.5/37 = 180.31

Итак средняя прибыль по всем банкам составляет 180.31 млн. руб.

б, в) Расчет среднего квадратического отклонения и коэффициента вариации.

Для изменения степени колеблемости отдельных значений признака от средней исчисляются основные обобщающие показатели вариации: дисперсия, среднее квадратическое отклонение, коэффициент вариации.

Дисперсия (²) – это средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической.

² = ((x – x)2*f) / f – взвешенная (3)

Среднее квадратическое отклонение () представляет собой корень квадратный из дисперсии и равно:

² = ((x – x)2*f) / f – взвешенное (4)

Коэффициент вариации (V) – относительный показатель вариации, который представляет собой процентное отношение среднего квадратического отклонения к средней арифметической:

V = (*100) / x (5)

По величине коэффициента вариации можно судить о степени вариации признаков, а следовательно, об однородности состава совокупности. Чем больше его величина, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу.

Оформим промежуточные данные для расчета дисперсии, среднего квадратического отклонения, коэффициента вариации в табличном виде.

Таблица 5

Группы банков по прибыли, млн. руб.	Число банков, f	Середина интервала, x_i	x	x_i- x	(x_i– x)²	*(x_i– x)²f**
62 - 117 118 - 173 174 – 229 230 – 285 286 и выше	7 13 8 5 4	89.5 145.5 201.5 257.5 313.5	180.31	- 90.81 - 34.81 21.19 77.19 133.19	8246.46 1211.74 449.02 5958.3 17739.576	57725.22 15752.62 3592.16 29791.5 70958.304
Итого	37	-	-	-	-	177819.81

Дисперсия

²= 177819.81 / 37 = 4805.94

2. Среднее квадратическое отклонение

 = 4805.94 = 69.32

Коэффициент вариации

V = (69.32*100) / 180.31 = 38.44%

4) Вычисление средней арифметической по исходным данным.

Исходные данные представлены в виде перечня прибыли по номерам банков, поэтому применим среднюю арифметическую простую:

x = x / n (6),

где x – сумма прибыли банков;

n – число банков.

x = 6609 ( по таблице 1)

x = 6609 / 37 = 178.62

Итак, средняя арифметическая рассчитанная по исходным данным составляет 178.62 млн. руб. А средняя арифметическая, рассчитанная по интервальному ряду, характеризующему распределение банков по прибыли составляет 180.31 млн. руб. Такие расхождения получились потому, что при исчислении средней арифметической в рядах распределения (пункт 3) возникает необходимость перехода от интервального ряда к дискретному, при этом допускается некоторая неточность, т.к. делается предположение о равномерности распределения единиц признака внутри группы. Эта ошибка тем меньше, чем уже интервал и чем больше единиц в интервале.

У нас интервал достаточно большой 56, а банков в каждой группе не много от 4 до 13, поэтому и получилась разница между средними арифметическими рассчитанными по различным данным:

180.31 – 178.62 = 1.69 млн. руб.

Выводы по результатам 1 задания.

В таблице 1 представлена зависимость между прибылью банков и их собственным капиталом, из которой можно сделать вывод, что величина прибыли находится в непосредственной зависимости от собственного капитала банка. Так например: в I группе, где сосредоточены банки с наименьшей прибылью (62-117) и собственный капитал банка не превышает 2020 млн. руб. А в Vгруппе, где собраны банки с максимальной прибылью (286 и выше) и собственный капитал доходит до 8587 млн. руб.

Из таблицы 2 можно сделать вывод, что более 75% (75.68%) банков получают прибыль менее 230 млн. руб.

На гистограмме наглядно представлена зависимость количества банков и получаемой ими прибыли (например: по гистограмме можно сказать, что наибольшее количество банков (13) получают прибыль в интервале (117-173) млн. руб.). Также по гистограмме графически определили значение моды (случайной величины, встречающейся с наибольшей вероятностью, в дискретном вариационном ряду).Она приблизительно равна середине интервала (117-173), т.е.145 млн. руб.

По графику комуляты определили значение медианы (варианта, находящегося в середине вариационного ряда).

Вычисление средней арифметической (180.31 млн. руб.) дало обобщающую характеристику прибыли по банкам, т.е. средняя прибыль по всем 37 банкам составляет 180.31 млн. руб.

По результатам вычисления дисперсии и среднего квадратического отклонения можно сделать вывод однородности совокупности и типичности средней величины (чем меньше значение дисперсии и среднего квадратического отклонения, тем более типичной будет средняя величина и однороднее совокупность). По решению: ² = 4805.94;

=69.32 млн. руб.Эти значения не достаточно малы, значит совокупность не однородна, а средняя не типична.

Также для характеристики однородности совокупности применяется коэффициент вариации. Совокупность считается однородной, если коэффициент вариации не превышает 33%, по решению он равен 38.44%, т. е. совокупность не однородна.

Выполняя 4 часть задания, рассчитали среднюю арифметическую по различным данным: по исходным данным (178.62) и по интервальному ряду (180.31). Получились числовые расхождения, которые объясняются необходимостью перехода от интервального ряда к дискретному, при вычислении средней арифметической по интервальному ряду.

Задание 2

По исходным данным:

Установите наличие характер связи между признаками прибыль и величина собственного капитала, образовав 5 групп с равными интервалами по обоим признакам, методами:

а) аналитической группировки,

б) корреляционной таблицы.

Решение

Для изучения связи между признаками - прибыль и величина собственного капитала, необходимо построить корреляционную таблицу и аналитическую группировку.

Корреляционная таблица – это специальная комбинационная таблица, в которой представлена группировка по двум взаимосвязанным признакам: факторному и результативному.

В нашем случае факторный признак – величина собственного капитала, результативный – прибыль.

Чтобы построить корреляционную таблицу, образуем 5 групп по факторному и результативному признакам.

По аналогии с первым заданием определим величину интервала:

Собственный капитал Прибыль

h = (x_max – x_min) / n h = (x_max – x_min) / n

h = (8587 - 440) / 5 = 1629.4 h = (342 – 62) / 5 = 56

Получим группы предприятий по

Факторному и Результативному

признакам.

440 – 2069.4; 2069.4 – 3698.8; 62 – 118; 118 – 174; 174 – 230;

3698.8 – 5328.2; 5328.2 – 6957.6; 230 – 286; 286 – 342.

6957.6 – 8587.

Построим корреляционную таблицу:

Таблица 6

Распределение банков по величине собственного капитала и прибыли

Собственный капитал, млн. руб.	Прибыль, млн. руб.
62 – 118	118 –174	174 – 230	230 – 286	286 – 342	Итого
440 – 2069.4 2069.4 – 3698.8 3698.8 – 5328.2 5328.2 – 6957.6 6957.6 – 8587	7	10 1 2	1 5 2	3 1 1	2 1 1	18 11 5 2 1
Итого	7	13	8	5	4	37

Из данных таблицы видно, что распределение числа банков произошло вдоль диагонали, проведенной из верхнего левого угла в правый нижний угол таблицы, т. е. увеличение признака «собственный капитал» сопровождается увеличением признака «прибыль».

Характер концентрации частот по диагонали корреляционной таблицы свидетельствует о наличии прямой тесной корреляционной связи между изучаемыми признаками.

Аналитическая группировка позволяет изучать взаимосвязь факторного и результативного признаков.

Основные этапы проведения аналитической группировки – обоснование и выбор факторного и результативного признаков, подсчет числа единиц в каждой из образованных групп, определение объема варьирующих признаков в пределах созданных групп, исчисление средних размеров результативного признака.

Результаты группировки оформляются в таблице.

Для установления наличия и характера связи между собственным капиталом и прибылью, сначала построим рабочую таблицу (интервалы те же, что и в корреляционной таблице).

Таблица 7

Распределение банков по величине собственного капитала

№ п/п	Группы банков по величине собственного капитала	№ банка	Собственный капитал, млн. руб.	Прибыль, млн. руб.
А	Б	1	2	3
I	440 – 2069.4	1 3 4 5 6 14 15 16 18 20 22 23 26 28 29 30 31 36	1969 840 1828 589 1368 1115 1076 1969 440 981 530 895 1079 985 2020 1576 1152 1517	62 83 153 118 170 66 121 129 67 148 198 163 165 64 111 119 93 153
Итого	18	22629	2183
II	2069.4 – 3698.8	7 8 9 12 19 24 25 27 33 35 37	2080 2400 3681 2971 2960 2818 3034 2918 2400 2338 2646	139 200 244 329 282 240 224 213 203 215 306
Итого	11	30246	2558
III	3698.8 – 5328.2	2 17 21 32 34	5207 4703 3808 3810 4077	175 166 165 189 237
Итого	5	21605	932
IV	5328.2 – 6957.6	10 13	5590 6930	268 289
Итого	2	12520	557
V	6957.6 – 8587	11	8587	342
Итого	1	8587	342
Всего	37	95587	6572

Blog

«Статистические методы изучения взаимосвязей финансовых показателей деятельности» банка

Содержание