Внастоящей курсовой работе рассмотрены следующие вопросы, раскрывающие основные статистические методы изучения взаимосвязей

Вид материала

Решение

Содержание ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Методы группировки Метод рядов Графические методы Классификация статистических графиков Определение формы связи между признаками Измерение тесноты корреляционной связи между признаками РАСЧЕТНАЯ ЧАСТЬ Задание 30 Аналитическая часть

Подобный материал:

• Контрольных, 56.64kb.
• «Статистические методы изучения взаимосвязей финансовых показателей деятельности» банка, 816.36kb.
• Внастоящей лекции представлена систематизация отечественных и зарубежных методов, 316.17kb.
• Методические указания по выполнению курсовой работы I. Основные задачи и назначение, 217.55kb.
• Программа исследования, 416.21kb.
• Вкурсовой работе рассмотрены следующие вопросы : Конкурентные стратегии предприятия, 853.98kb.
• Литература Введение, 229.71kb.
• Бодрийяр, «Система вещей» ? Вопросы к зачету = вопросы к контрольной работе 17 июня, 61.96kb.
• Учебно-методическое пособие содержит следующие структурные разделы: введение, цели, 335.07kb.
• Методические указания к курсовой работе по дисциплине «численные методы», 134.12kb.

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ

Общественные явления, на каком бы уровне они ни наблюдались, не могут рассматриваться в отрыве друг от друга и всегда являются взаимосвязанными. Изменения одной составляющей жизни общества обязательно влечет за собой изменения другой или других составляющих, причем это влияние может быть как непосредственным, хорошо заметным, так и опосредованным, когда его нелегко увидеть «невооруженным глазом». Именно эти факторы обусловливают актуальность темы данной курсовой работы, и поэтому важно хорошо представлять себе основные статистические методы изучения взаимосвязей общественных явлений, уметь ими пользоваться и анализировать результаты исследования.

В настоящей курсовой работе рассмотрены следующие вопросы, раскрывающие основные статистические методы изучения взаимосвязей:

1. Методы группировки, их основные виды. Аналитическая группировка как основной способ изучения взаимосвязи признаков.

2. Построение рядов распределения. Метод параллельных рядов.
   
3. Графический метод в статистике Основные виды, функции и свойства статистических графиков.
   

В расчетной части работы решена задача №30. Выявлена зависимость между нераспределенной прибылью и инвестициями в основные фонды различными методами, описанными в теоретической части. Измерена теснота связи между указанными признаками.

В аналитической части работы исследована взаимосвязь между размером среднедушевых доходов в Липецкой области в 2000 – 2001 годах и стоимостью минимального набора продуктов питания с помощью освоенных методов. Так же была измерена теснота связи между этими признаками.

Для расчетов в настоящей работе был применен табличный процессор Microsoft Excel.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Методы группировки

В результате статистического наблюдения получают первичные данные о единицах совокупности, которые на следующем этапе статистического исследования – этапе сводки – обобщаются в группы и систематизируются. Статистическая сводка – это приведение собранной информации к виду, удобному для проведения анализа. Простая сводка заключается в простом подсчете общих итогов, сложная – в группировке единичных данных в группы по однородному признаку, подсчете итогов по ним и представлении результатов в виде статистических таблиц [1].

Определение группировки можно сформулировать следующим образом: группировка — это процесс образования однородных групп на основе расчленения статистической совокупности на части или объединение изучаемых единиц в частные совокупности по существенным для них признакам [2]. Результатом осуществления этого процесса является разделенный на группы объект наблюдения.

Признаки, по которым производится распределение единиц наблюдаемой совокупности на группы, называются группировочными признаками, или основанием группировки.

Принято выделять следующие основные задачи, решаемые с помощью метода статистических группировок: образование социально экономических типов явлений; изучение строения изучаемых явлений и структурных изменений, происходящих в них; выявление связи между изучаемыми признаками. Для решения этих задач соответственно применяют типологические, структурные и аналитические группировки [2]. В рамках настоящей работы целесообразно подробно рассмотреть содержание и этапы построения аналитической группировки.

Так, аналитические группировки используются для изучения явления и связи между отдельными признаками. По роли, которую играют признаки во взаимосвязи изучаемых явлений, их подразделяют на факторные, воздействующие на другие признаки, и результативные, испытывающие на себе влияние факторных. В роли факторных и результативных признаков могут выступать как качественные (атрибутивные) признаки, так и количественные. Причем в зависимости от сложившихся объективных условий и цели исследования признаки могут меняться ролями [3].

При проведении аналитической группировки сначала обосновывают и выбирают факторный и результативный признаки. В основу группировки кладется факторный признак.

После определения факторного и результативного признаков необходимо установить распределение единиц совокупности по группам. При прочих равных условиях чем больше число групп, тем меньше величина интервала и наоборот. Одним из основных требований является выбор такого числа групп и величины интервала, которые позволяют более равномерно распределить единицы совокупности. Критерием правильности группировки является оптимальная наполняемость интервалов. Количество групп во многом зависит от того, какой признак служит основанием группировки. Так, нередко атрибутивные группировочные признаки предопределяют число групп (группировка работников по образованию, продавцов по категориям). По аналогии также расчленяется совокупность по дискретному признаку, изменяющемуся в незначительном диапазоне (при группировке магазинов по числу товарных секций, семей — по числу их членов и др.).

Интервалы групп устанавливаются при значительной колеблемости дискретного признака (торговая площадь, число работников) и при непрерывно изменяющемся количественном признаке (величина зарплаты, сумма издержек обращения и т. д.).

Под величиной интервала обычно понимают разность между максимальными и минимальными значениями признака в каждой группе.

В практике статистических группировок правильное установление величины интервала имеет первостепенное значение для образования качественно однородных групп. Например, нельзя объединять в одну группу явления, которые относятся к разным частным совокупностям. При характеристике работы производителей товаров по уровню выполнения ими договоров нецелесообразно образовывать группу 95—105%, а надо образовать две группы: 95—100%, 101 – 105%.

В зависимости от степени колеблемости группировочного признака, характера распределения статистической совокупности устанавливаются интервалы равные или неравные. При более или менее равномерной разности между верхней и нижней границами интервалов устанавливаются одинаковые границы во всех группах.

Число групп тесно связано с объемом совокупности. Здесь нет строго научных приемов, позволяющих решать этот вопрос при любых взаимосвязях названных величин. Однако при равенстве интервалов для ориентировки существует формула, предложенная американским ученым Стерджессом, с помощью которой можно наметить число групп при известной численности совокупности N [4]:

n = 1+ 3,322 lg N (1)

Зная размах колеблемости значений изучаемого признака во всей совокупности и намечаемое число групп, величину равного интервала можно определить по формуле

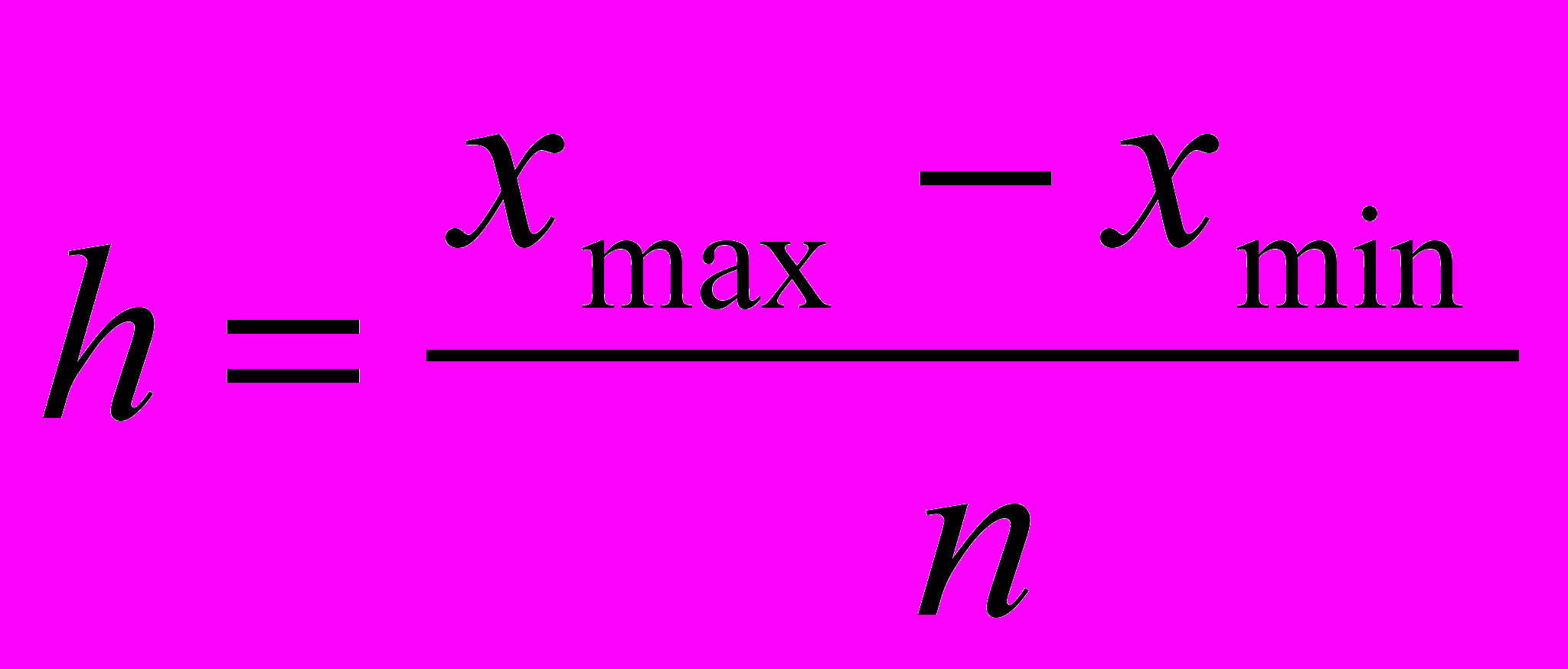(2)

где x_max и x_min -максимальное и минимальное значения признака.

При определении величины интервала и распределении единиц объекта наблюдения по группам важно точное установление границ, которые в большинстве своем обозначаются указанием значений признака «от» и «до» для единиц, включаемых в данную группу. В практике построения группировки нередко (при непрерывно изменяющемся признаке) одно и то же число служит верхней и нижней границами двух смежных групп. Например, группы работников магазина по производительности труда обозначаются так: до 90 тыс. руб., 90—120, 120—150, 150—180, свыше 180 тыс. руб. При таком построении интервалов вопрос об отнесении единиц объекта наблюдения по группам в практике решается двояко: по принципу «включительно» к первой группе относится работник, производительность труда которого обозначается «до 90 тыс. руб.»; по принципу «исключительно» этот работник включается во вторую группу: 90 – 120 тыс. руб. В практике применяются оба метода, но предпочтительнее принцип «исключительно».

Намечаемые при группировке интервалы бывают открытые (у них указана одна граница – верхняя или нижняя) и закрытые (имеющие нижнюю и верхнюю границы). Необходимость в открытых интервалах обусловлена большой колеблемостью изучаемого признака, разбросом его количественных значений, требующих образования множества групп, если отделять их обеими границами.

Серединное значение интервалов определяется несколькими приемами. Этот показатель можно рассчитать суммированием верхней и нижней границ интервала и делением суммы пополам. Вычитая величину равного интервала из серединного значения второго интервала, будем иметь середину первого (105 + 30), а середина последнего, открытого интервала определяется прибавлением длины интервала к середине интервала из предпоследней группы (165+30=195).

Затем для каждой группы рассчитывают средние значения результативного признака и прослеживают, какое влияние оказывает изменение факторного признака на результативный. Результаты группировки оформляются в таблице.

Таблица – это наиболее рациональная форма представления результатов статистической сводки. Значение статистических таблиц состоит в том, что они позволяют охватить материалы статистической сводки в целом. Например, для изучения связи между явлениями и их признаками строят корреляционную таблицу.

Корреляционная таблица — это специальная комбинационная таблица, в которой представлена группировка по двум взаимосвязанным признакам: факторному и результативному [4].

Концентрация частот около диагоналей матрицы данных свидетельствует о наличии корреляционной связи между признаками.