Гайдей Наталья Викторовна, учитель Iкатегории муниципальной общеобразовательной школы №168 с углубленным изучением предметов художественно-эстетического цикла г. Новосибирска. Тип урок
| Вид материала | Урок |
СодержаниеХод урока 3 группа. Дробно–рациональные уравнения II. Устная работа. |
- Ядрышникова Вера Викторовна, учитель муниципальной общеобразовательной школы №168, 40.13kb.
- Публичный доклад, 209.93kb.
- «Разработка модели школы с углубленным изучением предметов художественно-эстетического, 2230.34kb.
- Программа развития муниципального автономного общеобразовательного учреждения Советского, 1148.81kb.
- Подготовили Новикова Елена Адольфовна, учитель начальных классов; Давыдова Елена Егоровна,, 108.71kb.
- Начало Великой Отечественной войны Подготовила: Реутова Елена Ивановна, учитель истории, 57.15kb.
- Урок литературного чтения по теме «И. А. Крылов «Мартышка и очки», 161.41kb.
- План конспект урока по литературе 7 класс, 63.96kb.
- Future Simple Tense Цели урок, 184.45kb.
- Руководители Программы: Колбина С. А., директор школы Лыскова Р. В., заместитель директора, 966.87kb.
Тема: «Уравнения».
Автор: Гайдей Наталья Викторовна, учитель I категории муниципальной общеобразовательной школы № 168 с углубленным изучением предметов художественно-эстетического цикла г. Новосибирска.
Тип урока: интегрированный (математика-информатика.)
Вид урока: урок обобщающего повторения по теме.
Класс: 9.
Количество часов: 1 час.
Материалы и оборудование:
- раздаточный материал (карточки с заданием),
- кодоскоп или проектор.
- компьютерный класс (программное обеспечение – тестовая программа).
Цели и задачи:
- Обобщить и закрепить методы решения всех типов уравнений;
- способствовать выработке навыка решения уравнений;
- определить степень подготовленности учащихся по теме: «Уравнения» к контрольной работе.
Ход урока:
I. Проверка домашнего задания.
Начинается урок с проверки домашнего задания, которое было дано по группам по разным уровням сложности. Заслушиваются сообщения выступающих, проверяются решения уравнений. Если встречаются ошибки, они учащимися исправляются. Проверка осуществляется с помощью кодоскопа: демонстрируются слайды с решениями уравнений из домашнего задания.
- 1 группа.
Линейные уравнения:
а) 2 - 3 (x + 2) = 5 - 2х;
x = -9.

б)
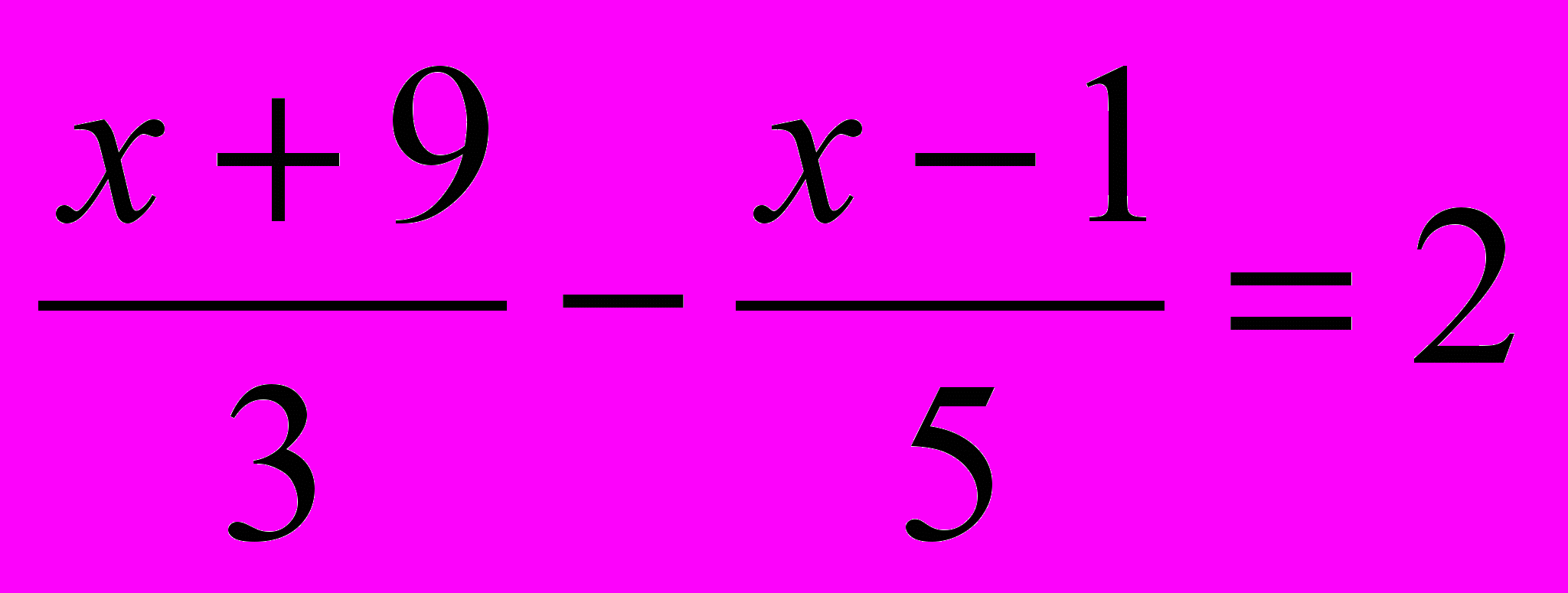 ;
;x = - 9.
- 2 группа.
Квадратные уравнения:
- полные квадратные уравнения
6х² - 7х +1= 0;
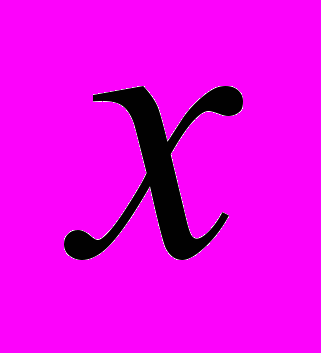 1=1; х2=
1=1; х2=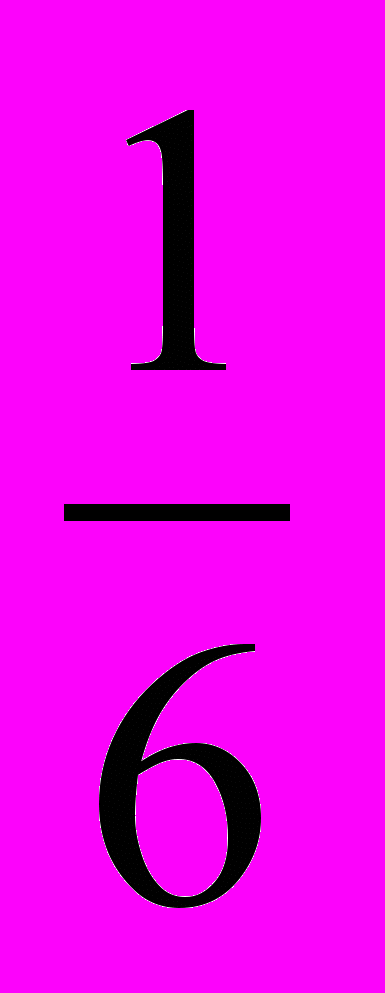 .
.- неполные квадратные уравнения
а) в = 0, 25 -100 x
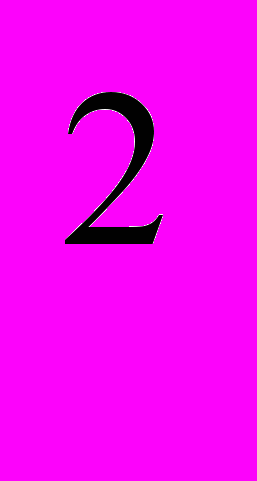 = 0.
= 0.x
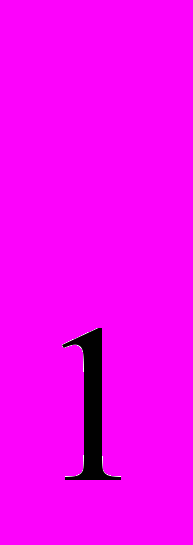 =
= 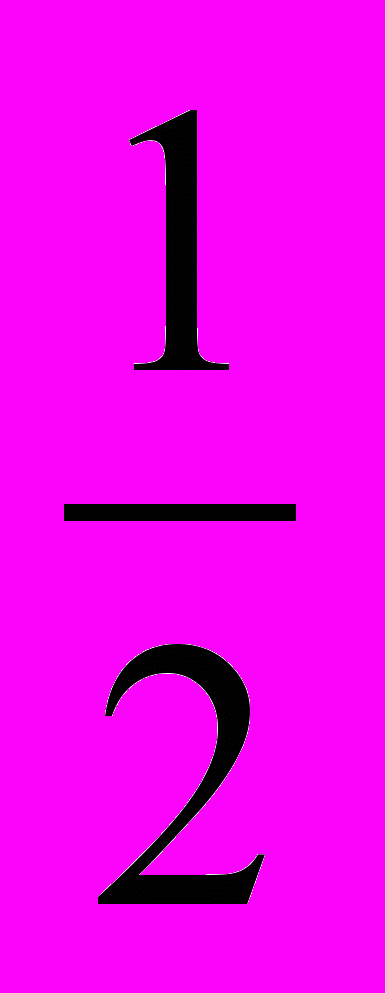 ; х2 = -
; х2 = -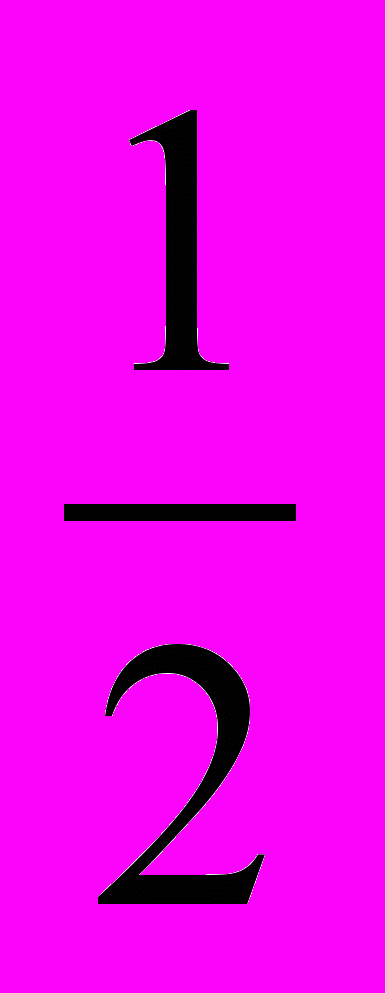 .
.б) с = 0, 3х² - 12х = 0.
х1= 0 ; х2 = 4.

-
3 группа.
Дробно–рациональные уравнения:
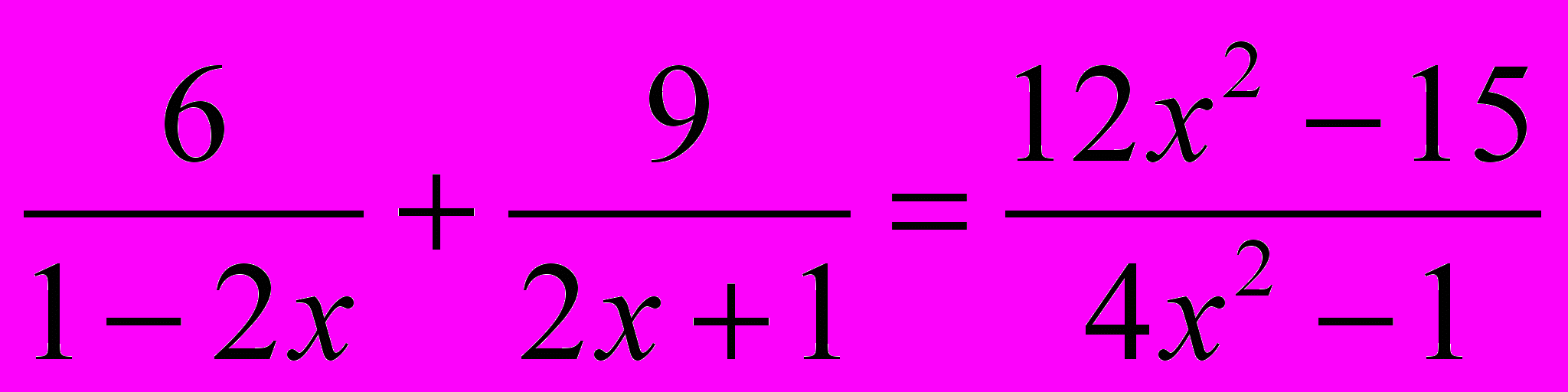 .
.6(2х+1) + 9(2х-1) = 12х2-15, если x = 0, то 4х2 -1 = 0-1, не равно 0.
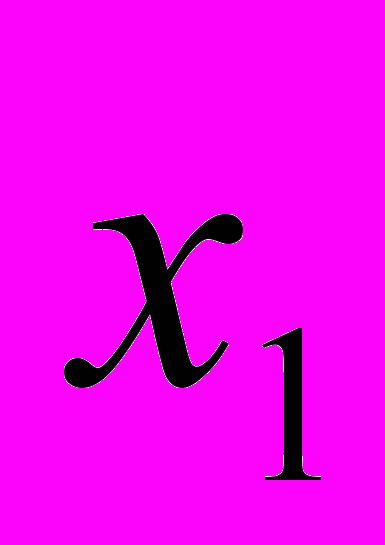 = 0;
= 0; 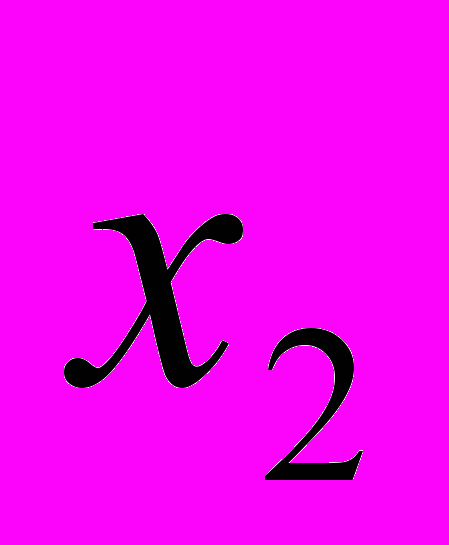 =
= 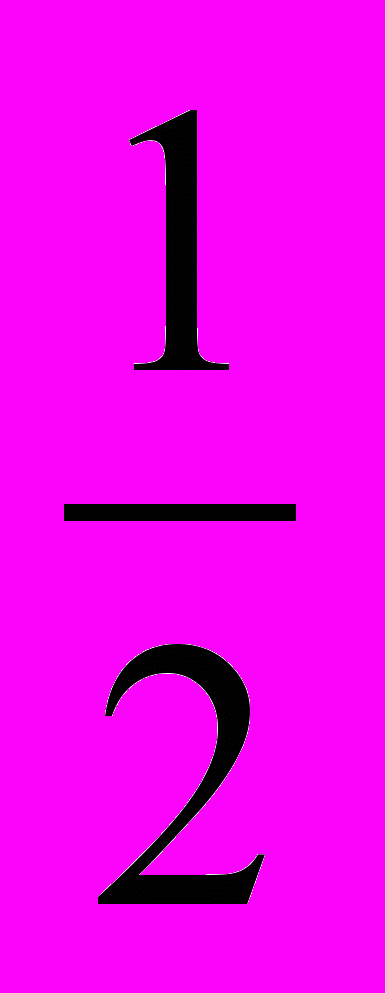 . если x =
. если x =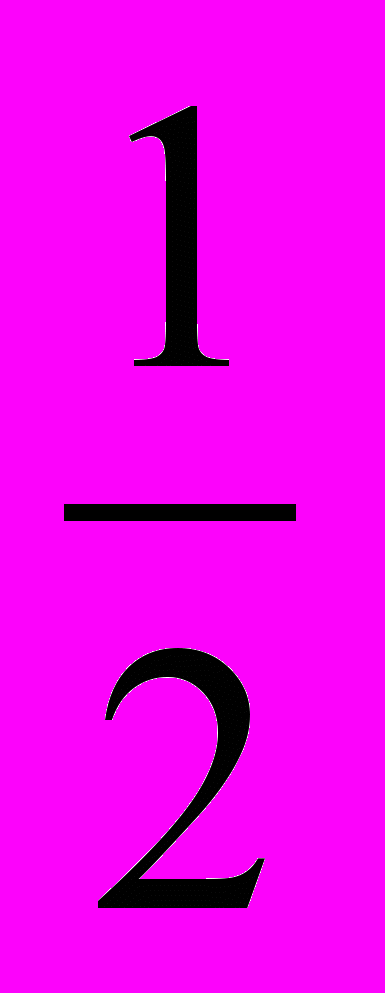 , то 4х2 -1 = 4*
, то 4х2 -1 = 4* 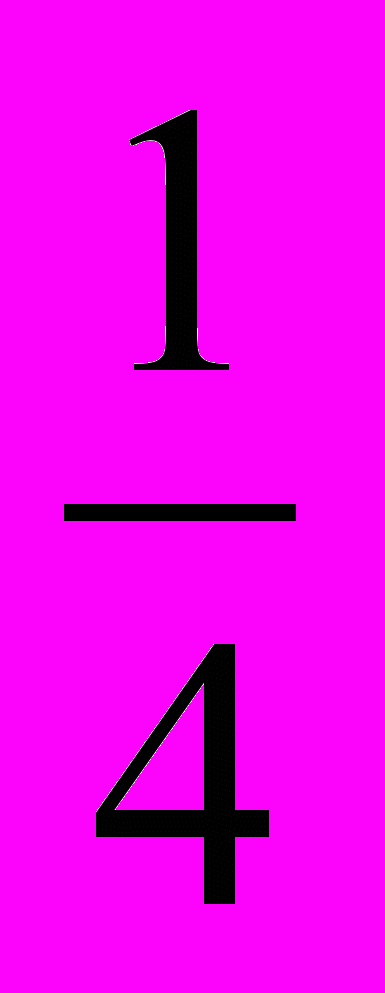 -1= 0.
-1= 0.ответ: 0

- 3 группа.
Алгебраические уравнения высших степеней:
- Биквадратные уравнения
2х4 – 19х2 +9 = 0.
Пусть у =
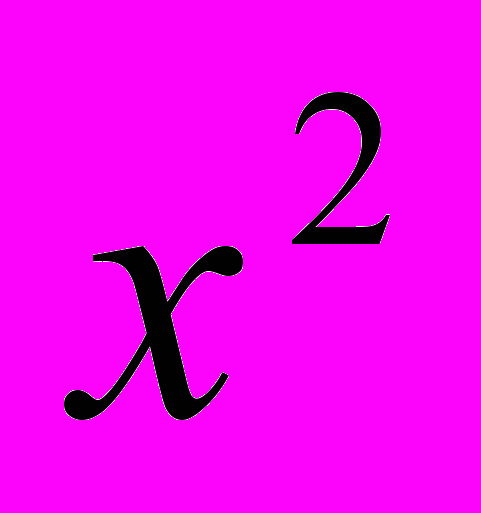 , тогда уравнение примет вид: 2у2 - 19у + 9=0.
, тогда уравнение примет вид: 2у2 - 19у + 9=0.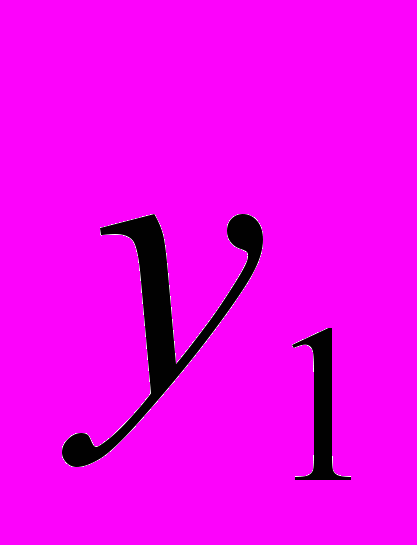 =9;
=9; 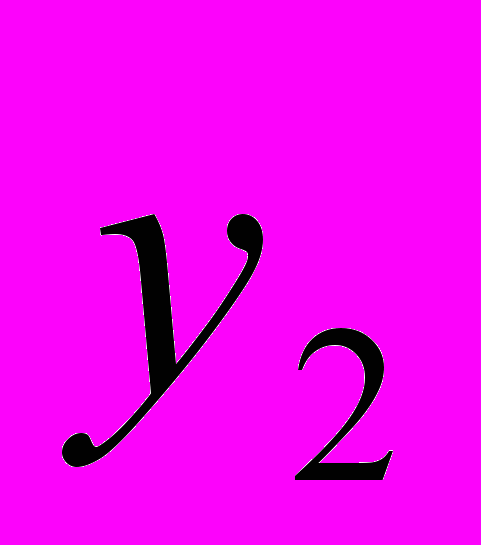 =
= 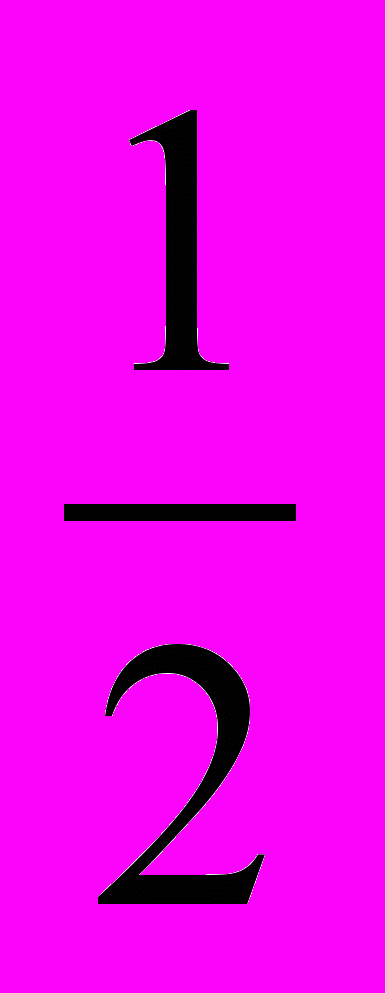 .
.Учитывая подстановку, имеем
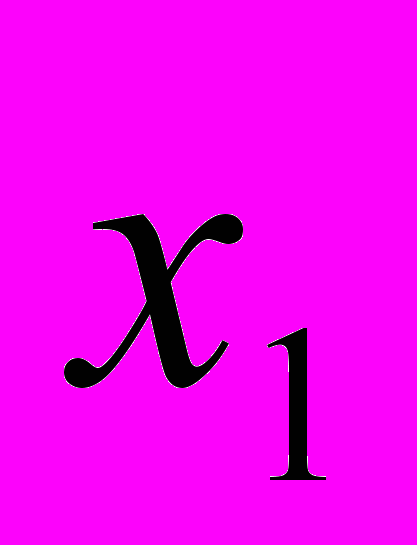 =
=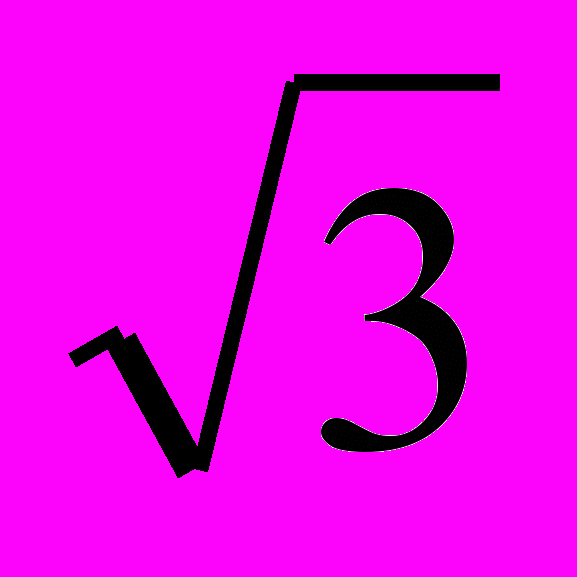 , x
, x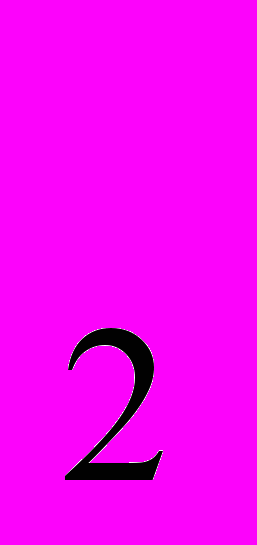 = -
= -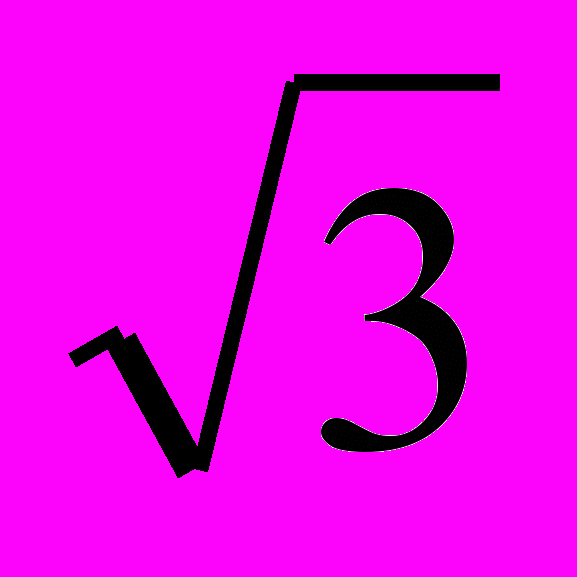 , х3=
, х3= 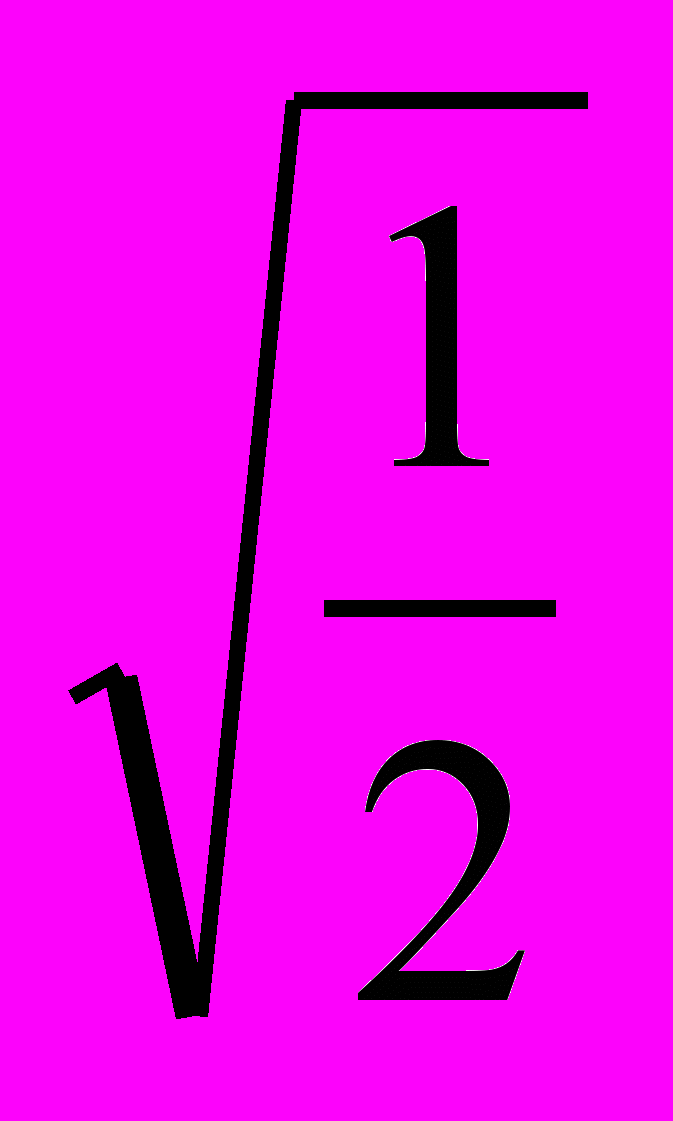
 , x
, x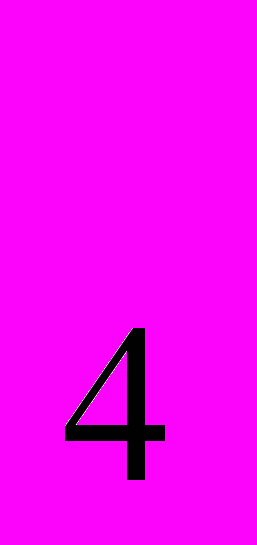 = -
= -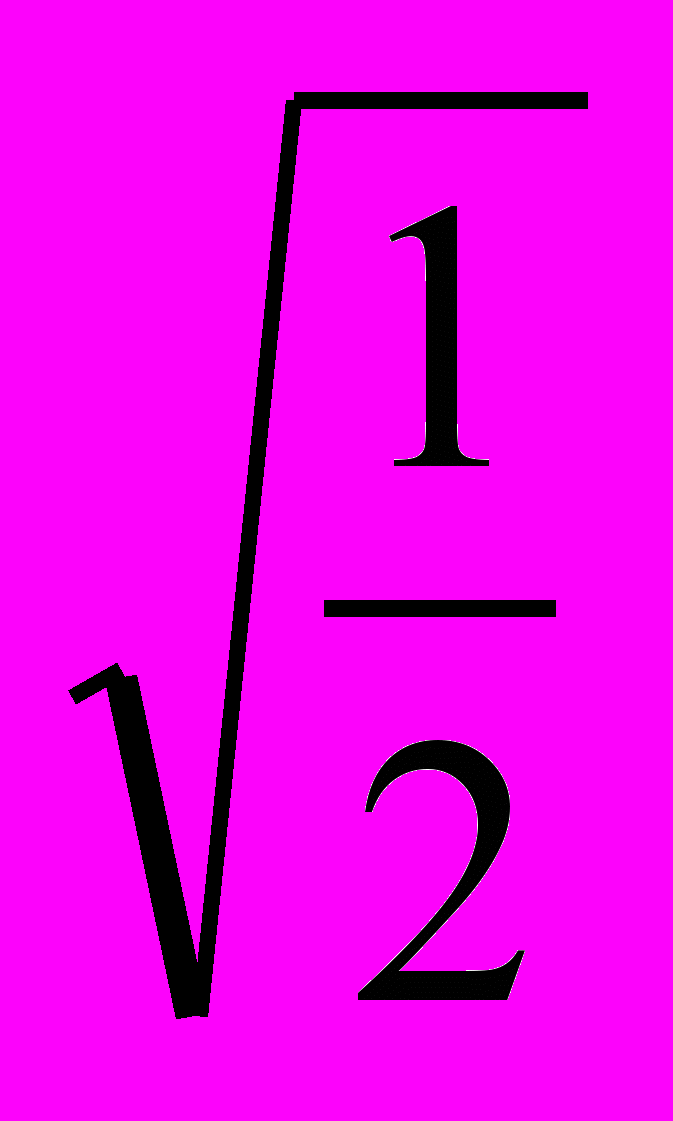 .
.- Введение новой переменной
(х2 + 4х) (х2 + 4х - 17) + 60 = 0.
Пусть у = x
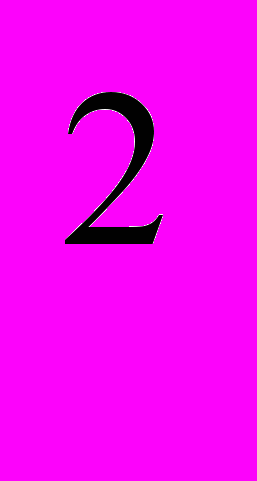 + 4х, тогда у (у-17) + 60 = 0, у1=12, у2=5.
+ 4х, тогда у (у-17) + 60 = 0, у1=12, у2=5.Учитывая подстановку, имеем:
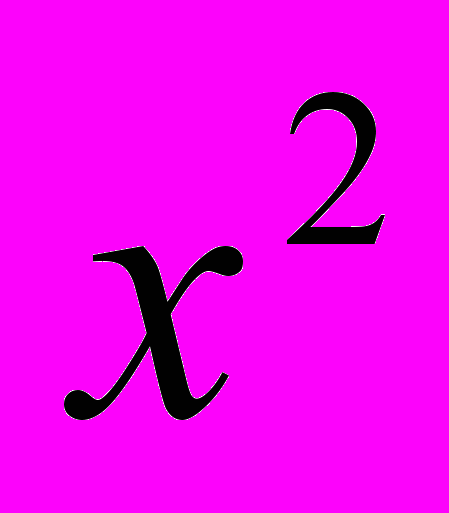 + 4х = 12 и х2 + 4х = 5
+ 4х = 12 и х2 + 4х = 5х1= 2, х2 = -6 х3 =1, х4 = -5
- Разложение левой части уравнения на множители
х3-2х 2-3х + 6 = 0.
(х-2)(х2-3)=0;
х1=2, х2 = -
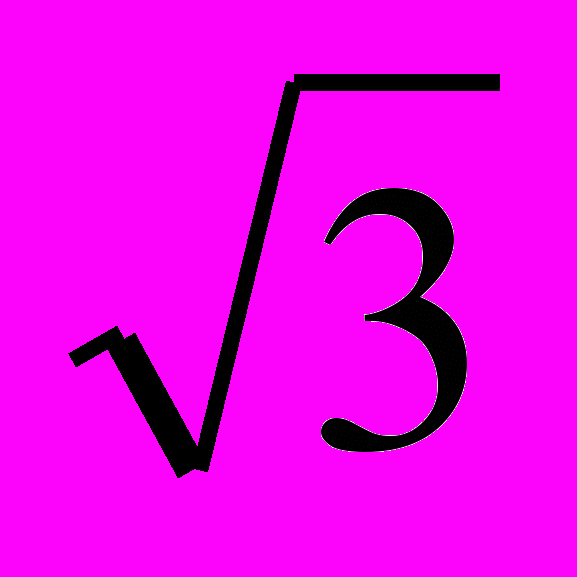 , х3 =
, х3 = 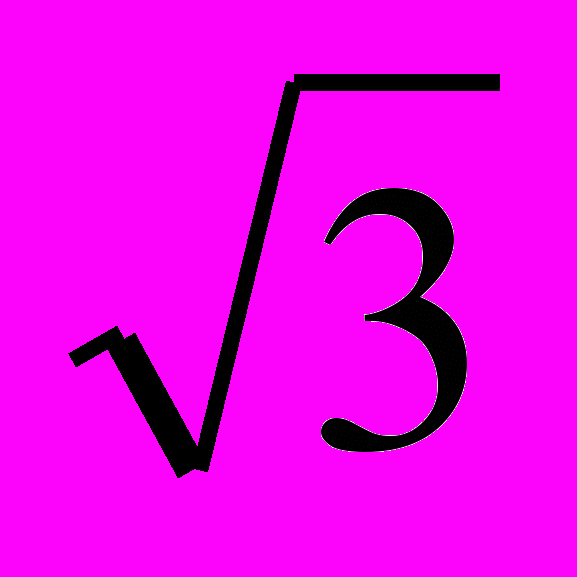 .
.
II. Устная работа.
Задание: из ряда представленных уравнений, определите, к какому виду относится уравнение и каким способом его можно решить (уравнения выведены на экран через кодоскоп).
1.
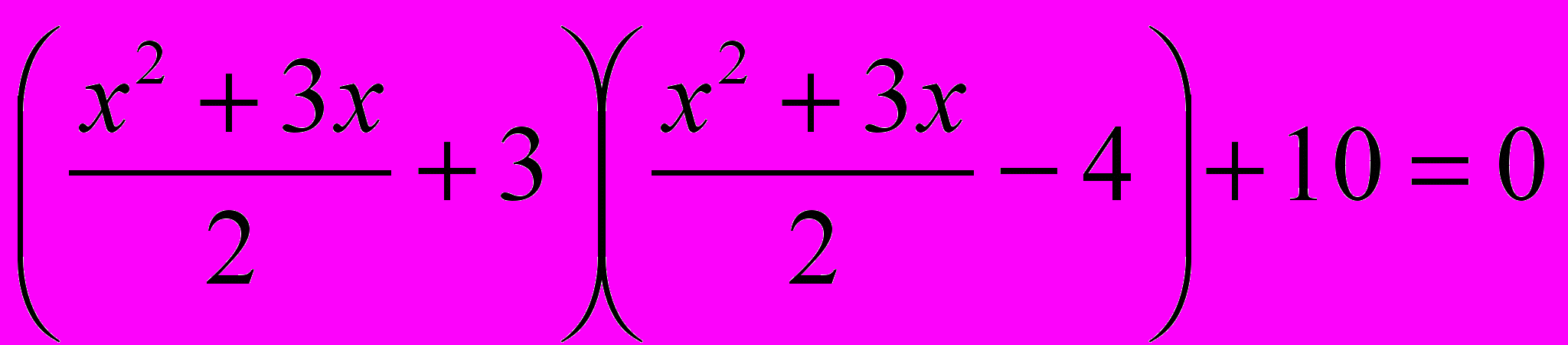 .
.2. 6х4-3х 3+12х2- 6х = 0.
3.
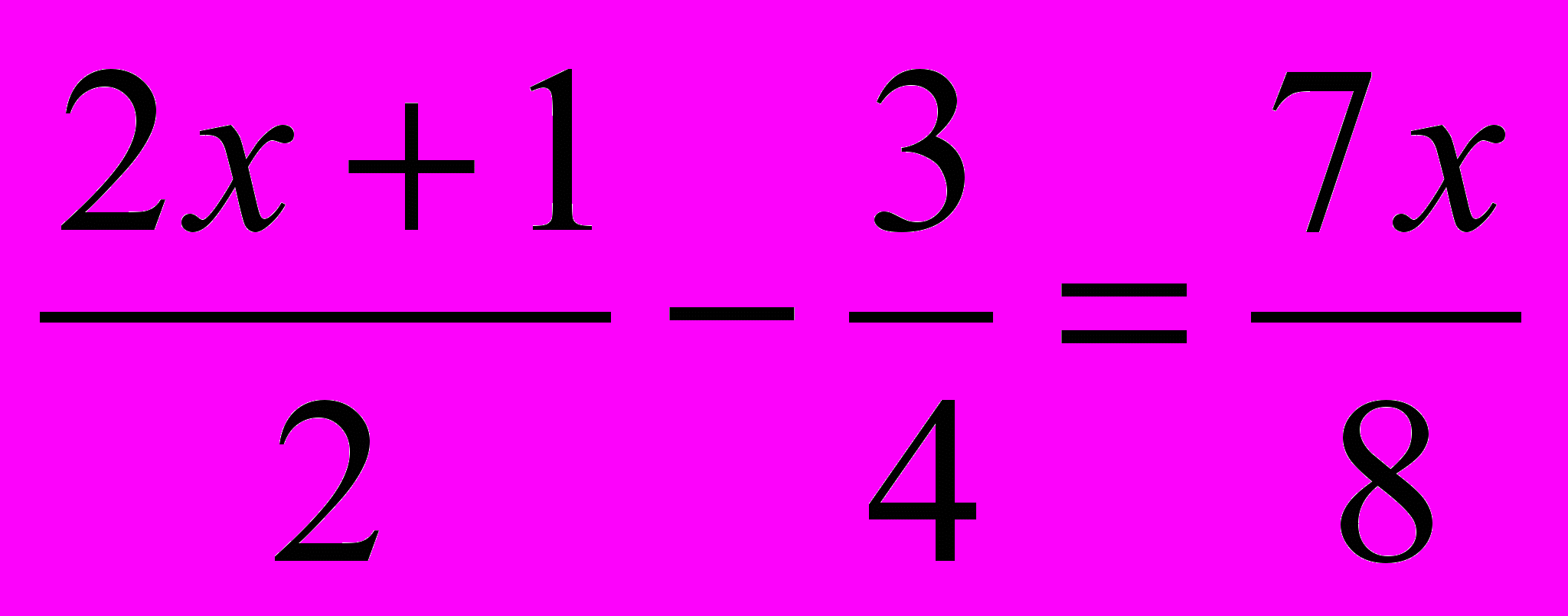 .
.4. (х-1)(5х + 0,5) = 0.
5. x(2х+1) = x + 4.
6. х6-7х3-8 = 0.
7.
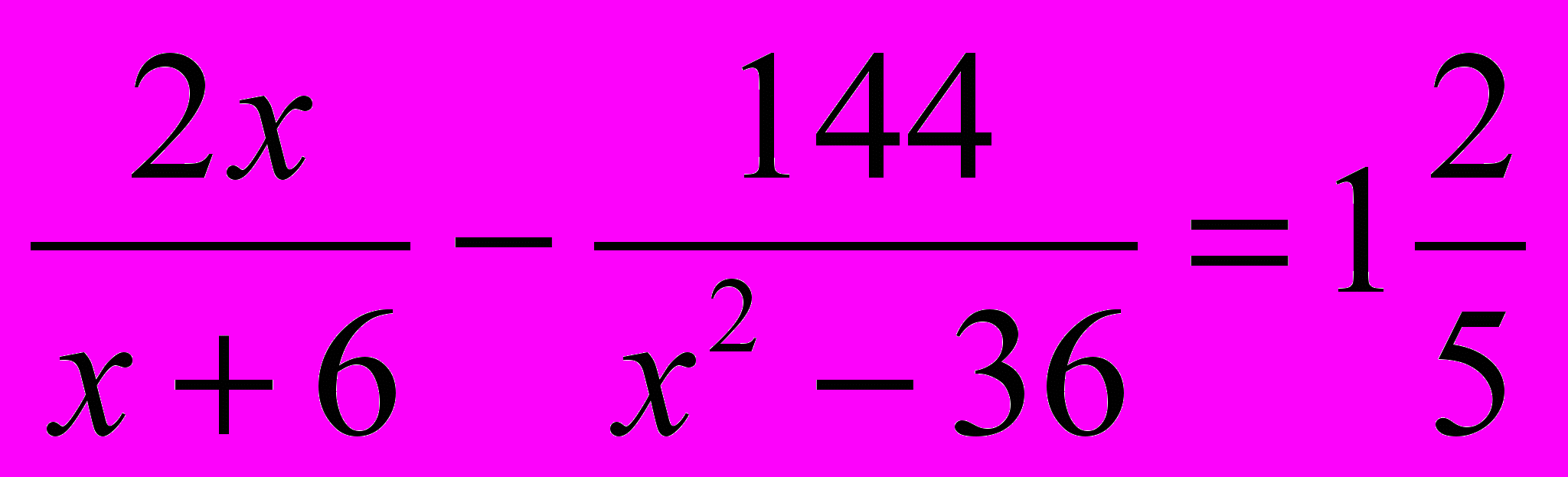 .
.- (х+1)2 - 0,81=0.
III. Самостоятельная работа учащихся
Работа «Проверь себя». Каждому ученику предлагается оценить свои возможности и выбрать самому уровень сложности самостоятельного задания (карточки разного уровня сложности – разного цвета).
- Желтая карточка - 1 уровень сложности:
- 5
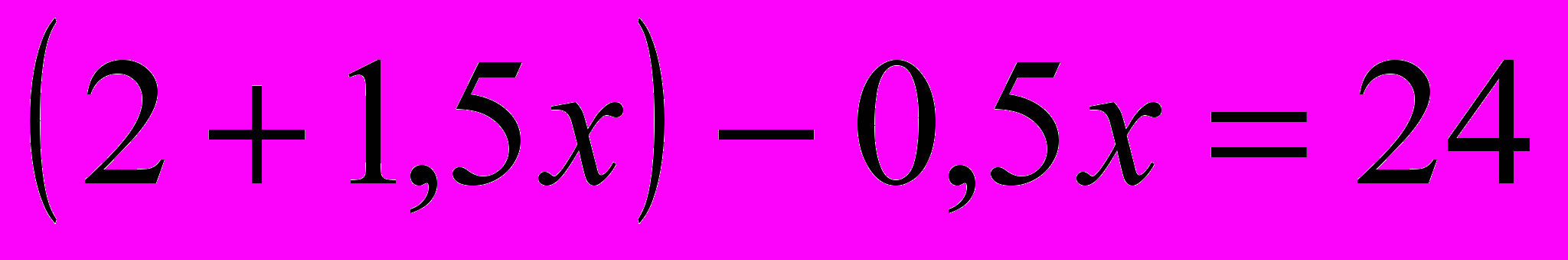
-
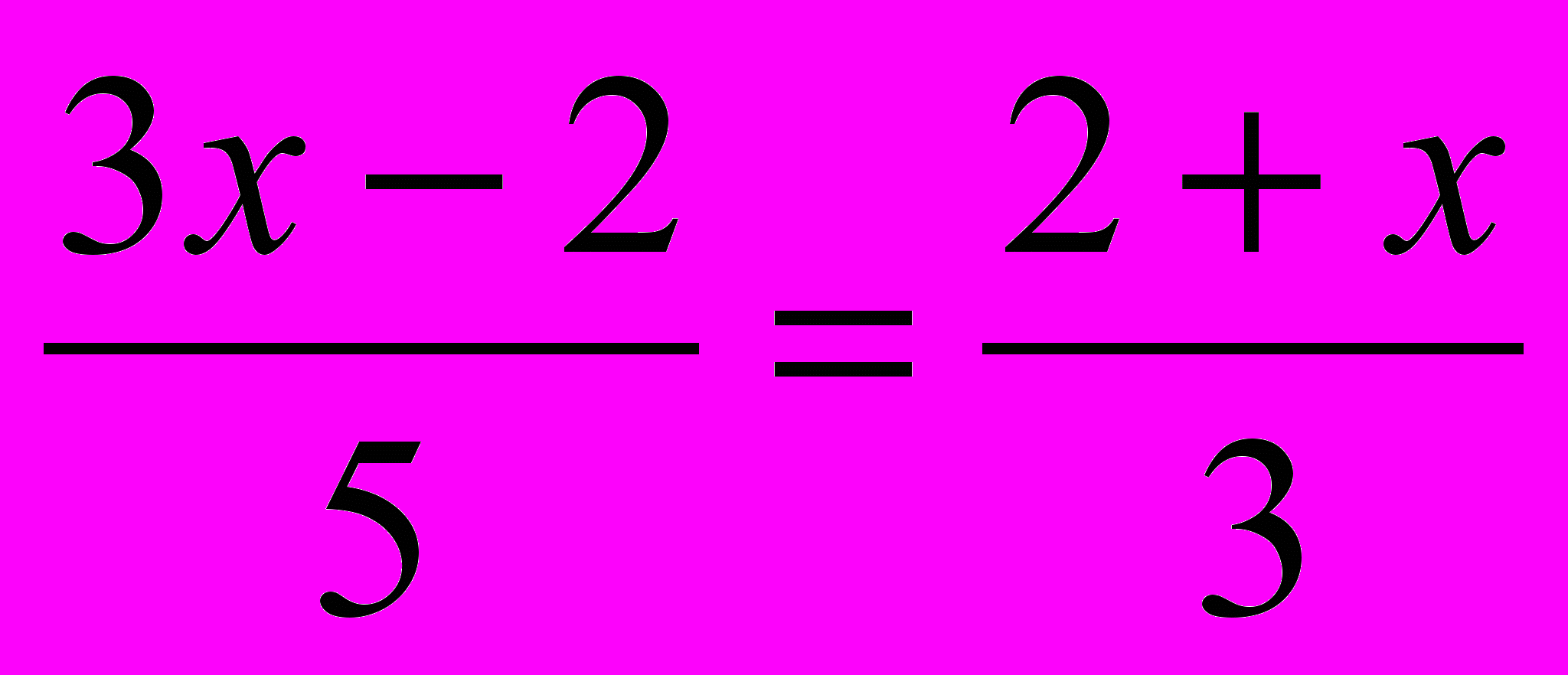
- 3x
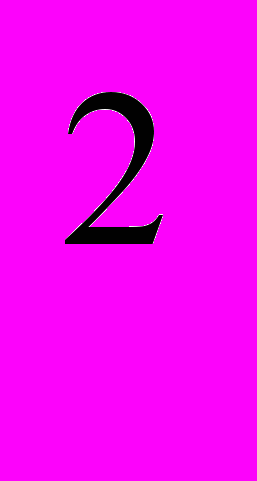 +7x-6=0
+7x-6=0
- Синяя карточка – 2 уровень сложности:
- x
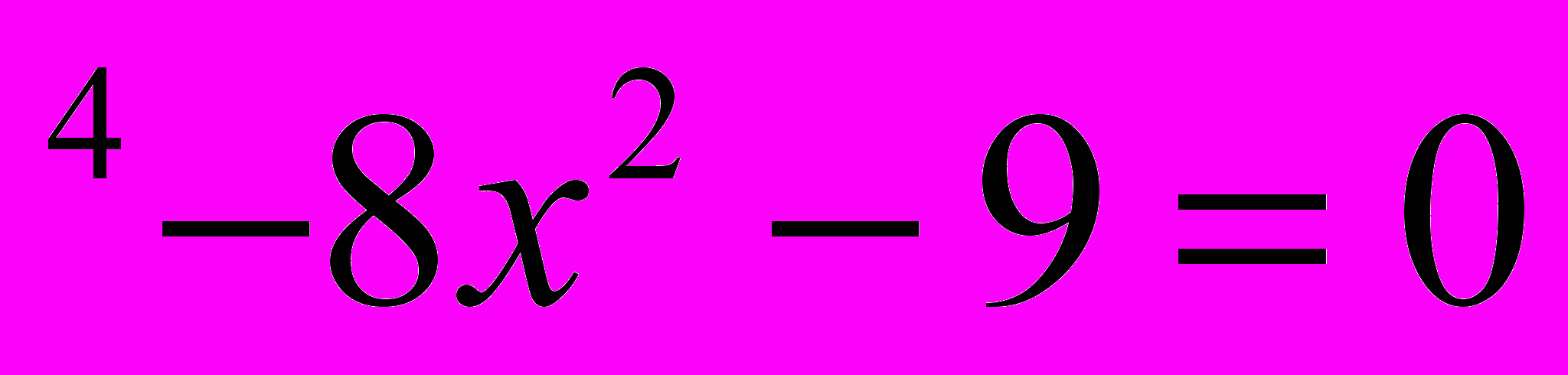
-
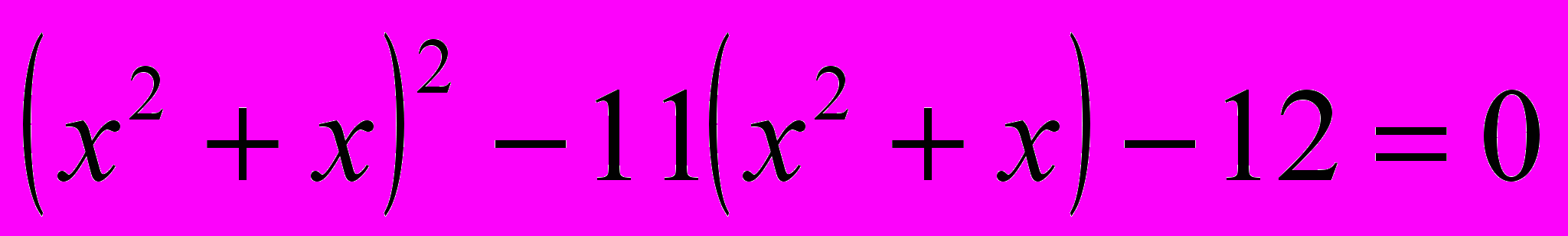
-
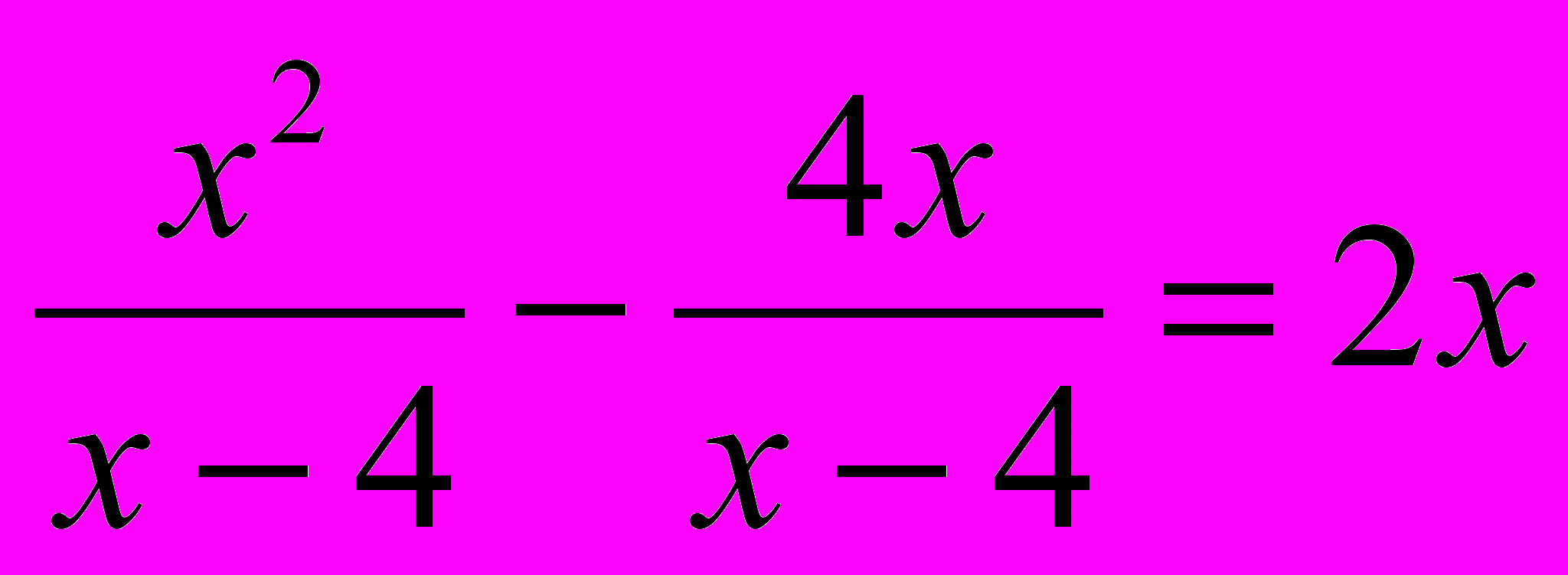
- Красная карточка – 3 уровень сложности:
- x
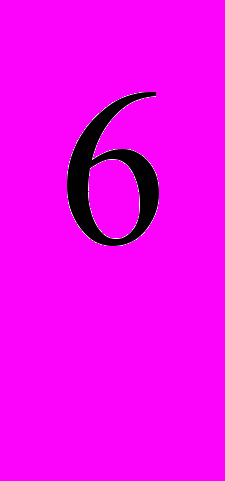 +5x
+5x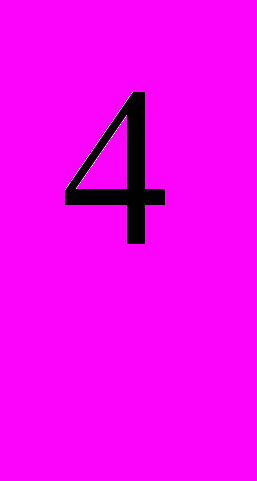 -x
-x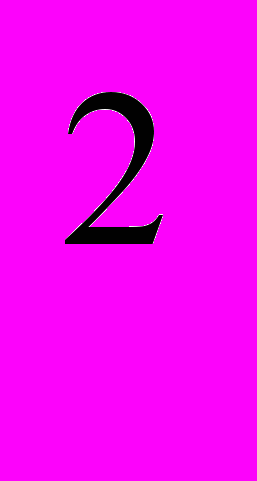 -5=0
-5=0
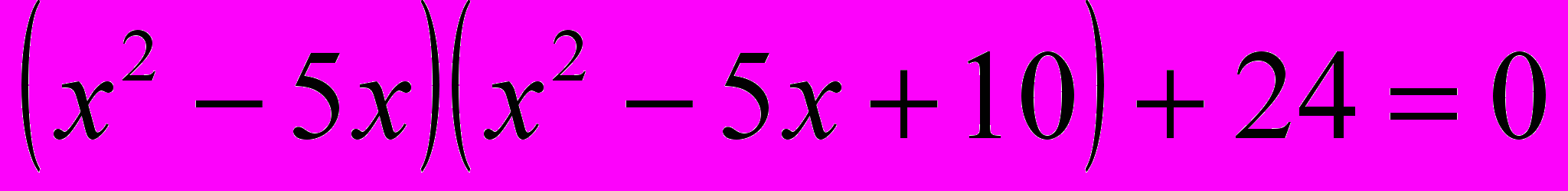
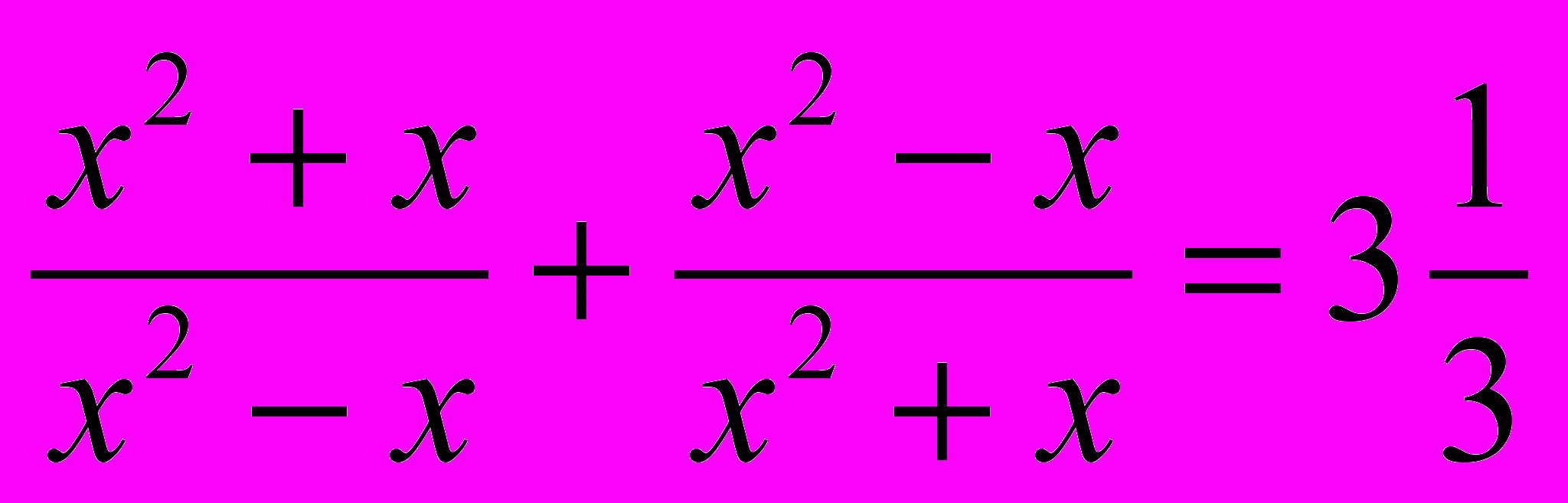
Проверка ответов производится с помощью тестовой программы на компьютере (можно использовать любую тестовую программу, позволяющую вводить данные). Учащиеся, выполнив выбранный уровень (кроме третьего), могут приступить к следующему. Для выполнивших 3 уровень, на дополнительную оценку предлагаются следующие уравнения:
- 2х4-5х3+6х2-5х+2 = 0, x=1;
- (х-1) (х-3) (х-5) (х-7) = 105, х1=0, х2=8.
IV. Подведение итогов урока.
В журнал выставляются «4» и «5», полученные за работу по карточкам.
IV. Домашнее задание:
Из сборника для подготовки к экзаменам:
Для всех: 1 раздел №№ 433, 440, 454, 459, 492.
Повышенный уровень сложности: 2 раздел №№ 92(1), 93(1), 94(1).
