Уроках математики (из опыта работы)

Вид материала

Урок

Содержание Метод обобщения Метод противопоставления – Родо - видовая схема Тема «четырёхугольники» Ход урока Вывод: квадрат частный случай ромба(отметим это на схеме). Итак

Подобный материал:

• Ерилова Г. Ф., учитель математики моу сош №33 г. Томска Нетрадиционные формы контроля, 248.47kb.
• Рабочая программа по курсу Формирование исследовательских умений на уроках математики, 51.16kb.
• Методика использования дидактических игр на уроках математики в начальной школе Содержание, 677.9kb.
• Опыта: «Активизация познавательной деятельности учащихся на уроках математики как условие, 294.4kb.
• Тема работы: Технологии психолого- педагогического взаимодействия с детьми зпр на уроках, 805.68kb.
• Аннотированный список ресурсов Интернет «Нравственное воспитание на уроках математики», 18.81kb.
• Ионовой Надежды Валентиновны на заседании рмо учителей математики 2007 2008 учебный, 108.68kb.
• Задачи: провести диагностическое исследование уровня развития творческого мышления, 149.7kb.
• Анализ работы мо учителей математики и информатики за 2008-2009 учебный год, 135.86kb.
• Уроках математики посредством сообщения им сведений из истории науки, 158.2kb.

РАЗВИТИЕ ПОЗНАВАТЕЛЬНОЙ АКТИВНОСТИ НА УРОКАХ


МАТЕМАТИКИ (из опыта работы)


Ларина В.Р., учитель высшей категории МОУ СОШ № 65

Мне неоднократно доводилось наблюдать на уроках математики отсутствие интереса у ряда учеников к предмету. Я попыталась выяснить причину такого безразличного отношения к приобретению нового и узнала, что причин несколько. Во - первых, это непонимания того, о чём говорит учитель, возникшее из-за того, что где-то раньше произошел разрыв понимания. Во-вторых, учитель не привёл достаточных доводов для введения нового, и учащиеся не видят необходимости получения этого, как им кажется, ненужного знания. В-третьих, ученик увлечён чем-то другим и его не интересует предмет, мешающий его увлечению. В-четвёртых, есть учащиеся которые не желают заниматься ничем, что требует малейшего умственного напряжения. Ко всем этим категориям учащихся нужны различные меры для восстановления нормального отношения к процессу обучения. Возник вопрос- «Как развить у детей стремление к знаниям?». Появился ответ- им должно быть интересно, учащиеся должны сами захотеть получить эти знания, т.е. необходимо повысить и активизировать их познавательную активность.

В процессе приобретения учащимися знаний, умений и навыков важное место занимает их познавательная активность, умение учителя активно руководить ею. Со стороны учителя учебный процесс, может быть управляем активно и пассивно. Пассивно управляемым процессом считают такой его способ организации, где основное внимание уделяется формам передачи новой информации, а процесс приобретения знаний для учащихся остаётся стихийным. В этом случае на первое место выступает репродуктивный путь приобретения знаний. Активно управляемый учебный процесс предполагает учёт индивидуальных особенностей школьников, моделирование учебного процесса, его прогнозирование, планирование, активное управление обучением и развитием учащегося. Учащиеся также могут проявлять пассивную и активную познавательную деятельность. Познавательная активность-это инициативное, действенное отношение учащихся к усвоению знаний, а также проявление интереса, самостоятельности и волевых усилий в обучении. Это определение очень широкое, т.к. включает в себя:

1. мотивы и цели деятельности;
   
2. интерес к предмету;
   
3. внимание к изучаемому объекту;
   
4. волевые усилия;
   
5. положительные эмоции;
   
6. творческую самостоятельность;
   
7. владение необходимыми способами и приёмами познавательной деятельности.
   

Познавательной активности школьник не будет проявлять, если он не получит удовлетворения от получаемых результатов, не знает или не видит путей применения знаний на практике. И в этом ему поможе, в первую очередь, сама математика. Раскрывая детям внутреннюю красоту математики, показывая силу её эмоционального воздействия, учитель помогает им учиться радостно, с интересом, побуждает их к творческому отношению к предмету. В данной работе я предлагаю несколько приёмов развития познавательной активности учащихся, которые используются мною на уроках в разной степени в зависимости от возраста ребят, материала, особенностей класса. это:

1. использование проблемного обучения, самостоятельность в получении знаний;
   
2. наглядность, доступность, открытость обучения;
   
3. оригинальность решений задач различными способами;
   
4. связь науки и практики;
   
5. самостоятельные и проверочные работы с использованием аналогий и тестирования;
   
6. творческие, поисковые задания учащихся;
   
7. использование на уроках элементов игры, историзма, занимательности;
   
8. различные формы работы с книгой;
   
9. изложение материала блоками, использование лекционно-семинарской системы;
   
10. наблюдение за речью учащихся и учителя;
    
11. внеклассная работа по предмету.
    
12. использование ИКТ на уроках.
    

Все предложенные приёмы рождались постепенно в течение многих лет работы, часть из них заимствована из опыта работы других учителей, часть – из книг, методических пособий, часть придумана мною. Но все они нравятся ребятам и мне как учителю. Рассмотрим подробней некоторые из них.


Для того чтобы познание математики доставляло учащемуся удовлетворение , нужно, чтобы он проник в суть идей этой науки и прочувствовал внутреннюю связь всех звеньев рассуждений, что только и позволяет понять логику математических доказательств. Если хотя бы раз ученик достигнет ясности в понимании существа дела, проникнет во внутреннюю связь понятий, рассуждений, логических выводов, то ему будет трудно удовлетвориться впоследствии суррогатом знаний, который даёт заучивание без понимания, зубрёжка без вдохновения. К состоянию полной ясности он станет стремиться сам, без напоминаний и принуждения, поскольку у него появится идеал знаний и тогда он поймёт: работа собственной мысли требует значительно меньших усилий и затрат времени, чем зубрёжка. Необходимо приучить мыслить учащихся самостоятельно, т.е. всемерно активизировать мыслительную деятельность каждого ученика на всех этапах урока. Для этого следует усилить использование проблемного обучения, т.е. создание таких ситуаций в процессе учебной деятельности, которые приводят учащихся к индивидуально-поисковой исследовательской деятельности. Проблемная ситуаций и постановка проблемы оживляют учебный процесс, вовлекают учащихся в продуктивную деятельность. Например, тема «Площадь треугольника» в геометрии 8 класса. Изложение материала можно построить следующим образом: урок начать с повторения формул площади прямоугольника и параллелограмма и решить одну- две соответствующие задачи. затем учащимся задаётся задача: «Найти площадь прямоугольного треугольника, если катеты равны 6см и 9см.». Возникла проблема. Анализируя, учащиеся предлагаю следующие пути решения: при помощи палетки; разбиением на квадратные см; дополнением до прямоугольника. Среди предложенных вариантов принимается третий. После решения задачи делается вывод о нахождении площади прямоугольного треугольника. Затем предлагается другая задача: «Вычислить площадь произвольного остроугольного треугольника» . при помощи дополнительных вопросов учителя – ученик находят способ решения этой задачи, достроив треугольник до параллелограмма. Таким же путём учащиеся предлагают найти площадь тупоугольного треугольника. Итогом рассмотрения этих задач может стать решение проблемы: « Найти площадь любого треугольника». Учащиеся смогут самостоятельно доказать эту теорему. Домашнее задание по этой теме тоже содержит в себе элемент проблемной ситуации:

1. Повторить теорему о вычислении площади треугольника. Попытаться найти другое доказательство.
   
2. Две стороны треугольника 18 и 24 см. Высота, проведённая к первой стороне равна 21см. Вычислить высоту, проведённую ко второй стороне.
   
3. Вывести формулу для вычисления площади равностороннего треугольника со стороной а.
   

Проблема может быть поставлена перед учащимися при помощи соответствующего вопроса в процессе решения некоторого задания, задачи, практической работы. Например, при введении понятия системы координат учащимся можно дать задание: укажите примеры из жизни, когда расположение предметов или состояние вещества описывается двумя числами. Учащиеся называют: шахматная доска, расположение корабля, театр, игра «Морской бой» и т.д. Ставится вопрос: как на плоскости можно определить положение точки? Учащиеся пытаются обобщить рассмотренные примеры и выделить аналогии. Проблема возникнет, если оставить задачу или пример , решаемый на уроке, незавершённым. Ученик вынужден решать самостоятельно поставленную задачу. Проблема возникает, когда перед учениками ставится задача, которую они не могут решить без дополнительных знаний. Например, ученики прекрасно справляются с уравнениями первой степени, но возникает проблема, как только они встречаются с неравенством второй степени. И начинают искать поиск решения этих неравенств. В практике очень часто используется обобщение или конкретизация ситуаций, поиск аналогий. Как показывает опыт, самостоятельная творческая деятельность учащихся, предваряющая объяснения учителя, успешно готовит к активному восприятию новых знаний, которые появляются как естественное продолжение уже имеющихся у учащихся знаний. Ученики становятся активными «творцами» нового, а не пассивными «запоминателями» их. Перед изучением теоремы Пифагора, её формулировку можно получить как результат решения задачи: найти соотношения между длинами сторон прямоугольного треугольника. Перед рассмотрением теоремы синусов, учащиеся выполняют домашнюю практическую работу:

• Построить три треугольника: прямоугольный, тупоугольный, остроугольный;
  
• Измерить стороны и углы треугольника;
  
• Вычислить отношение стороны к синусу противолежащего угла;
  
• Сравнить результаты.
  

Такие проблемные ситуации можно создать практически на каждом уроке и совместно с учащимися успешно с ними справляться, что способствует активизации познавательной деятельности учеников, их учебным работам придаёт творческий характер, развивает мышление.


Чаще всего урок состоит из изложения теории и решения нескольких иллюстрирующих её задач. Поэтому сама задача, приёмы её решения, анализ условия нечасто бывают объектом особого внимания. Учат же решать задачи, формируют навык исследовательской работы уроки, на которых ученик является активным участником поиска решения, испытывая при этом и радость открытий, и горечь поражений, когда выбранный путь приводит в тупик. Например, тема урока «Площадь поверхности правильной пирамиды». Сначала с учащимися мы разбираем решение практической задачи: на плакате изображён павильон и чертёж его крыши, вид сверху. Четыре ската крыши – равносторонние треугольники со стороной 6м, имеются два слуховых окна. От учащихся требуется указать, что нужно знать для расчёта расходов на покраску этой крыши. Ученики отвечают: расход краски на 1м², площадь поверхности крыши, цену краски, оплату выполнения работы. Общим обсуждением намечается план решения задачи: вычислить площадь одного из треугольников; найти площадь боковой поверхности правильной четырёхугольной пирамиды, полученное значение уменьшить на величину двух слуховых окон. От задачи мы переходим к модели правильной пирамиды. Я ставлю вопрос: « Что нужно знать, чтобы найти площадь боковой поверхности правильной пирамиды?» Ученики выводят формулу для вычисления площади поверхности правильной пирамиды. Урок заканчиваем самостоятельной работой : каждому даётся модель пирамиды и предлагается вычислить её площадь поверхности. При решении задач только одним способом у учащихся единственная цель- найти правильный ответ. Если же требуется применить при этом несколько способов, школьники стараются отыскать наиболее оригинальное, красивое, экономичное решение. Для этого они вспоминают многие теоретические факты, методы и приёмы, анализируют их с точки зрения применимости к данной задаче. Уроки, на которых рассматривается несколько способов решения задач, я называю уроки-«бенефисы». Перед этим учащиеся разбиваются на 3-4 группы по 2 человека, которые получают одну и ту же задачу. Им предлагается предоставить решение и показать его на уроке. Красивое решение находится после того, как придумано несколько вариантов. На уроке учащиеся защищают своё решение, а класс оценивает, кто дал более оригинальное, интересное решение , участвует в рецензировании работы своих товарищей. (приложение №1) Такая форма работы способствует стимулированию творческой деятельности школьников.


Ещё один способ, с помощью которого можно изгнать скуку, равнодушие с уроков, создать положительные эмоции у школьников - это творческие, исследовательские, поисковые задания. При составлении поисковых заданий я руководствуюсь следующими требованиями:

1. поисковые задания должны быть ориентированы на всех учащихся. Этому требованию отвечают задания средней трудности, посильные учащимся, но вместе с тем предполагающие при их выполнении проявление наблюдательности, обращения к анализу, синтезу, сравнении и т.д.
   

поисковые задания должны быть тесно связаны с основным учебным материалом. Целесообразно подбирать блоки родственных заданий, объединенных одной математической идеей или проблемой. Каждая задача высвечивает отдельную грань исследуемой проблемы. Сама же серия задач позволяет её всесторонне изучить. Рассмотрим примеры (приложение №2). Мощным инструментом для обучения и воспитания учащихся для развития их творческих познавательных способностей являются творческие задания:

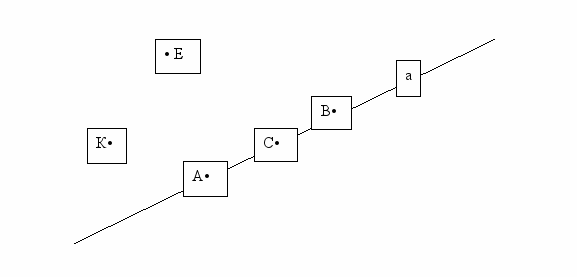
1. На первых уроках геометрии семиклассники знакомятся с различными простейшими фигурами, их отношениями, появляется новая терминология, которая нелегко усваивается ими. В связи с этим в устные упражнения каждого урока геометрии включаю следующие задания: описать рисунок.
   

Д•

Дана прямая а. Её можно назвать АВ, ВС, АС. Даны 6 точек: А, В, С, Д, Е ,К. точки Е и Д лежат по разные стороны от прямой а. И т.д. от урока к уроку рисунки усложняются. Также предлагаю ученикам самим придумать рисунки, а затем их описать.

2. Один из трудных методов доказательства, с которым ученики встречаются при изучении геометрии 7 класса – доказательство методом от противного. Ученикам предлагается проиллюстрировать применение доказательства методом от противного на примерах из жизни, художественной литературы, из различных школьных учебников. Примеры были из биологии, физики, из литературы – Шерлок Холмс.
   
3. Часто по окончании изучения темы предлагаю учащимся самостоятельно составить задачу и решить её, или сочинить сочинение в любой форме.
   

Применение лекционно-семинарской системы при изучении ряда тем курса позволяет учителю излагать учебный материал крупными порциями и на этой основе высвободить время для повторения теории и решения задач. Такая организация занятий обеспечивает усиление практической и прикладной направленности преподавания , приобщения учащихся к активной работе с учебной литературой, повышения уровня их подготовки. Уроки-лекции - один-два урока, на котором излагается весь теоретический материал изучаемого раздела. Во время школьной лекции я постоянно привлекаю учащихся, задавая вопросы, ставя проблемы. Показываю образцы решения несложных задач. На уроках-практикумах проводится целенаправленная работа по выработке у учащихся умений и навыков решения основных типов задач. Работа проводится дифференцированно, с учётом интересов и способностей учащихся. Также на этих уроках провожу обучающие самостоятельные работы. Уроки-семинары - чаще всего посвящены повторению, углублению и обобщению пройденного материала. Учащимся заранее сообщается теория, по которой будет проходить опрос и номера задач, приёмами, решения которых должны овладеть учащиеся. Подготовка к семинару является для учащихся одновременно и подготовкой к зачёту и контрольной работе. Один из вариантов распределения учебного материала (приложение № 3)

Я в своей работе использую основные методические идеи укрупнения дидактических единиц, в основном это в двух направлениях: совместное изучение родственных аналогичных тем (метод обобщения) и совместное (параллельное) изучение взаимообратных действий (метод противопоставления).

Метод обобщения – это интегрирование общих свойств. Признаков родственных понятий в одно целое с последующей затем дифференциацией по их отличительным признакам. Перед учащимися ставится задача: увидеть и осмыслить взаимосвязь и взаимозависимость, а также различие между этими понятиями, установить причины их сходства и различия.

Метод противопоставления – это параллельное совместное изучение двух взаимообратных действий с последующим их соединением в один целый процесс. Перед учащимися ставится задача: увидеть тесную взаимосвязь между обратными, противоположными действиями, что способствует формированию у них умения анализировать ход любых преобразований, устанавливать причинно-следственные связи между действиями, контролировать и проверять свои действия выполнением обратных действий.

Применение этой технологии на уроках математики, что особенно важно, позволяет снизить затраты времени на изучение всей темы в целом. А это в свою очередь, позволяет больше времени выделить на решение задач и практических упражнений. Применение данной технологии возможно не ко всем темам курса математики. Я применяю её к следующим темам:

Метод обобщения – геометрия 7-9 классы

• Треугольники 7 класс
  
• Четырёхугольники 8 класс
  
• Площадь 8 класс
  
• Векторы 9 класс
  
• Движения 9 класс
  

Алгебра 7-9 классы

• Формулы сокращённого умножения 7 класс
  
• Прогрессии 9 класс
  
• Системы линейных уравнений 7 класс
  
• Уравнения и системы уравнений 9 класс
  

Метод противопоставления – геометрия 7-9 классы

• Параллельные прямые 7 класс
  

Алгебра 7-9 классы

• Умножение одночлена на многочлен и вынесение общего множителя за скобки 7 класс
  
• Умножение многочлена на многочлен и разложение многочлена на множители способом группировки 7 класс
  

В качестве небольшого примера приведу тематическое планирование темы

«Четырёхугольники» 8 класс. При изучении семейства всех выпуклых четырёхугольников метод обобщения наиболее подходит, что позволяет изменить структуру преподношения материала. На изучение всей темы по программе отводится 14 часов, а я использую 11 часов:

• 2 часа на определение всех видов четырёхугольников здесь же составляется родо-видовая схема (см. приложение №4)
  
• 4 часа на изучение всех свойств четырёхугольников и на решение простейших задач
  
• 3 часа на решение комбинированных задач
  
• 2 часа на повторение и контрольную работу.
  

3 оставшихся часа использую по разному: для работы над ошибками, для индивидуальной работы с учащимися, не справившимися с работой, для индивидуальной работы с сильными учащимися.

В качестве практической реализации на уроках метода обобщения хочу предложить план-конспект первого урока по теме «Четырёхугольники» ( см. приложение №5)

Самый эффективный инструмент, побуждающий учащихся к более глубокому познанию предмета, развивающий их способности и воспитывающий интерес к математике является использование на уроках элементов историзма, игры, занимательности. Изложение новой темы, нового раздела математики лучше начинать с вводной части, возбуждающей интерес и внимание учащихся. Такой вводной частью может быть 3-5 минутный увлекательный рассказ, связанный с историей математики. Сообщение сведений из истории науки не только полезно в познавательном плане, но и такое изложение даёт возможность показывать учащимся при изучении каждого нового раздела или темы, что математика как наука о пространственных формах и количественных отношениях реального мира возникла и развивалась в связи с практической деятельностью человека. История математики, как и история любой другой науки, изобилует примерами, позволяющими решать вопросы воспитания учащихся.Действительно, ознакомление учащихся с жизнью и творчеством отечественных учёных имеют огромное воспитательное значение в формировании у школьников чувства патриотизма, понятия долга и преданности к Родине. Например, при изучении простых и составных чисел, говоря о роли знаменитых математиков , таких как Евклид , Эратосфен, в становлении и развитии теории чисел, обязательно рассказываю об огромном вкладе в эту область великого русского математика П.Л.Чебышева(1821-1894). Первый урок в 5 классе всегда начинаю с рассказа о развитии математики, о практической значимости математики в развитии других наук, о Л.Ф.Магницком, который написал первый русский учебник математики «Арифметика сиречь наука числительная», изданный в 1703г. во всех отношениях примером безупречного патриотизма является жизнь и деятельность Н.И.Лобачевского, гениального математика, общественного деятеля, блестящего педагога, патриота своей родины. Хотя имя «Коперника геометрии» известно многим учащимся, но не любой из них имеет достаточное представление о том, какой переворот в науке сделал Лобачевский открытием неевклидовой геометрии. В качестве примера приведу план урока (или внеклассного мероприятия), посвящённый жизни и научной деятельности Н.И.Лобачевского (приложение №6). Исторический материал может быть использован на любом этапе урока. Иногда эти сведения полезно дать перед объяснением нового материала, иногда органически связать его с отдельными вопросами темы урока, а иногда дать как обобщение или итог изучения какого-нибудь раздела, темы курса математики. Под занимательностью на уроке понимаем те компоненты урока (способы подачи учебного материала, специфические свойства информации и заданий, связанные с учебным материалом, а иногда и с организацией обучения),которые содержат в себе элементы необычного, удивительного, неожиданного, комического, вызывают интерес у школьников к учебному предмету и способствуют созданию положительной эмоциональной обстановки учения. Одним из видов занимательных заданий являются дидактические игры: игровая ситуация, когда ученика увлекает форма задания; математическая игра, когда ученика увлекает содержание задания. Чаще всего эти идёт сочетание этих двух видов. Современная дидактика, обращаясь к игровым формам обучения на уроках, справедливо усматривает в них возможности эффективной организации взаимодействия педагога и учащихся, продуктивной формы их общения с присущими им элементами соревнования, непосредственности, неподдельного интереса. Игра-творчество, игра- труд. В процессе игры у детей вырабатывается привычка сосредотачиваться, мыслить самостоятельно, развивается внимание, стремление к знаниям. Увлекшись, дети не замечают , что учатся: познают, запоминают новое, ориентируются в необычных ситуациях, пополняют запас представлений, понятий, развивают фантазию использование игровых ситуаций или игры на уроке не даёт возможность учащимся овладеть математикой «легко и счастливо». Легких путей в науку нет. Игру не нужно путать с забавой, не следует рассматривать её как деятельность, доставляющую удовольствие ради удовольствия. На игру нужно смотреть как на вид преобразующей творческой деятельности в тесной связи с другими видами учебной работы. Математические игры и игровые ситуации можно использовать либо на отдельном моменте урока, либо на каком – то его этапе, либо на всём уроке ( уроки-КВН, уроки-сказки, уроки-путешествия и т.д.) (приложение № 7). Например, опрос учащихся в начале урока можно провести в виде соревнования. Правила соревнования просты: все учащиеся разделяются на команды, от каждой команды поочерёдно выходит представитель, которому команды соперников задают по одному вопросу ( круг вопросов известен, они из домашнего задания). На обдумывание ответа и его запись на доске даётся не более 5 секунд и сразу объявляется оценка. Учитель выступает в роли арбитра; регистрирует участников и их ответы, ставит оценки, одним словом, ведёт протокол соревнования. В конце подводятся итоги, т.е. определяется сумма баллов, полученной каждой командой. Команда, набравшая больше баллов, считается победительницей и награждается призовым баллом, который она прибавляет к оценке одного из участников. При повторении большого теоретического материала перед изучением новой темы очень удачно можно провести опрос по парам. Учащиеся 1 варианта – «учителя», 2 варианта - «ученики». Учитель задаёт вопрос, «ученики» поворачиваются лицом к «учителю» и начинают вполголоса отвечать. Когда в парах обсуждены ответы, поднимается один из школьников и громко отвечает на поставленный вопрос. Учитель комментирует его ответ и попутно указывает, какие ошибки услышал сам, когда ходил по классу. Учащийся 1 варианта берёт листок бумаги и против номера вопроса ставит один из трёх знаков: «+»- верный ответ, «-» - неверный ответ, «±»- неточный ответ. В зависимости от количества знаков ставится оценка. После закрепления нового материала можно провести математическую викторину. Доска разделена на три части по числу рядов в классе. На каждой части доски учитель записывает баллы, которые «зарабатывает» во время викторины соответствующий ряд. Каждый вопрос имеет свою «цену», её заранее сообщают классу. Например, 1 балл - знание понятия или определения, 2 балла- решение стандартной задачи, 3 балла- решение нестандартной задачи. после викторины ребята выполняют самостоятельную работу, учитель в это время подсчитывает баллы. Итог викторины подводится в конце урока. При устном счёте очень удобной является игра – математическая эстафета. Каждый ряд получает таблицу с «форточками», т.е. с незаполненными клетками. Таблицы совершенно одинаковые. Таблицу кладут на первую парту справа. По команде: «На старт! Внимание! Марш!» - ученик, сидящий справа начинает заполнять «форточку». Закрыв, пустую клетку, он передаёт таблицу своему соседу и т.д. Последний учащийся в ряду, выполнив задание, бежит к учительскому столу, чтобы быстрее положить на него карточку. Первые ряд, сдавший работу, получает дополнительно 1 очко. Учитель проверяет правильность заполнения карточки и ставит оценку. Все эти примеры очень маленькая часть различных игровых ситуаций или игр применяемых мною на уроке. Но самое главное, что я поняла - использование математических игр на уроках повышает интерес к математике, вносит разнообразие и эмоциональную окраску в учебную работу, снимает утомление, развивает внимание, сообразительность, чувство соревнования, взаимопомощь. Словом, игры заслуживают право дополнить традиционные формы обучения и воспитания школьников.


Чтобы научить ребёнка чётко мыслить, полноценно логически рассуждать необходимо, воспитывать культуру речи у наших молодых граждан, прививать привычку, о которой раньше говорили: «Мыслям должно быть просторно, а словам тесно». Речь должна быть убедительной, краткой, ясной и одновременно изящной, возбуждающей мысль и эмоции. На уроках я постоянно уделяю внимание не только к содержанию, но и к форме ответа. Требуя от учащихся полных ответов на любой вопрос, я в то же время приучаю их к тому, что даже в обычной речи следует избегать пустой болтовни, засорённой лишними словами и фразами. От учащихся требуется при ответе произносить только то, что позволяет полностью раскрыть суть вопроса, при этом доказывая и обосновывая свой ответ. Но и к своей речи я тоже предъявляю повышенные требования. Каждое слово учителя, каждый сделанный им жест должны способствовать восприятию учащимися предмета изложения, процессу запоминания, содействовать развитию мышления учащихся. Речь учителя должна быть не только грамматически и литературно правильной, насыщенной идейным содержанием, но и эмоциональной, чтобы овладеть вниманием учащихся, направлять их сознание к достижению определённой цели. Она должна быть не слишком медленной, так как при этом теряется нить изложения, но не должна быть излишне быстрой, поскольку большинству учащихся за ней трудно уследить. Учитель должен быть психологом, чтобы уметь улавливать настроение аудитории, и воспользовавшись этим, увлечь слушателей рассказом и повести за собой, за предметом изложения. Для установления взаимного согласия и заинтересованности учителю и его слову принадлежит огромная роль.


Приёмов, методов, способов, позволяющих активизировать познавательную деятельность учащихся, существует много. Невозможно рассказать обо всех. Но самое главное, о чём должен помнить любой учитель- обучение может приносить радость каждому обучающемуся, и этого следует добиваться; при этом возникает полезный и для ученика и для учителя интеллектуальный контакт, позволяющий избежать насильственного процесса передачи знаний, когда учащийся сопротивляется, а учитель пытается заставить его получить определённую порцию новых сведений. Преподаватель должен так излагать свой предмет, чтобы заинтересовать учащихся, быть доступным для понимания. Ни в коем случае не должно быть места скуке, она – нежелательная гостья в любую пору обучения. Например, превосходный математик и педагог первой половины 19 века М.В.Остроградский так сформулировал это положение: « …скука является самой опасной отравой. Она действует беспрестанно; она растёт, овладевает человеком и влечёт его к наибольшим излишествам…». Если учащийся уже увлечён предметом, то эта отрава не так опасна, поскольку он требует не столько увлекательности, сколько содержательности изложения.


Приложение №4


РОДО - ВИДОВАЯ СХЕМА

Четырёхугольники



Параллелограммы


Трапеции






Прямоугольники

Ромбы

Прямоугольные


Равнобедренные


Квадраты

Приложение №5

ТЕМА «ЧЕТЫРЁХУГОЛЬНИКИ»


Цели урока:

1. 
   Познакомить учащихся со всеми видами четырёхугольников во взаимной связи друг с другом
   
2. Развивать логические умения и навыки ( анализ, синтез, обобщение, работа с понятиями и т. д.)
   
3. Воспитание интереса к предмету, усидчивости, трудолюбия
   

Методы: ведётся урок методом целесообразных вопросов или вопросно-ответного метода, опираясь на знания учащихся. Перед ними ставится проблемные вопросы, их ответы обсуждаются и обобщаются.


Ход урока:

1. 
   Повторение и актуализация знаний учащихся об основных понятиях геометрии, о взаимном расположении прямых и отрезков на плоскости, величин углов , понятие многоугольника и его элементов, понятие треугольника и его элементов – 10 мин.
   
2. Изучение нового – 20 мин
   
3. Домашнее задание -3 мин.
   
4. Первичное закрепление 10 мин.
   
5. подведение итогов – 2 мин.
   

Повторение: фронтальная работа с классом в виде вопрос-ответ

2. Какие фигуры в геометрии называются основными? Почему? Привести примеры.
   
3. Что имеется у любой фигуры? Сколько существует фигур? От чего это зависит?
   
4. Как могут располагаться прямые на плоскости?
   
5. Что такое отрезок? Сравнение отрезков?
   
6. Что такое многоугольник? Его элементы и периметр.
   
7. Что такое треугольник? Его элементы и виды.
   

Изучение нового: в виде беседы, где перед учащимися ставятся проблемные вопросы

1. Среди множества геометрических фигур есть такие, у которых 4 стороны, 4 вершины , 4 угла, т.е. четырёхугольники. Сконструируем четырёхугольник как фигуру, полученную при пересечении пары произвольных прямых другой парой произвольных прямых.
   

А В




Д С


Замкнутая линия, ограниченная этими прямыми, является четырёхугольником. АВСД – четырёхугольник.

2. Дадим определение четырёхугольника. Четырёхугольник – фигура, состоящая из четырёх точек и четырёх последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой и отрезки не пересекаются.
   

Примеры фигур, не являющимися четырёхугольниками:

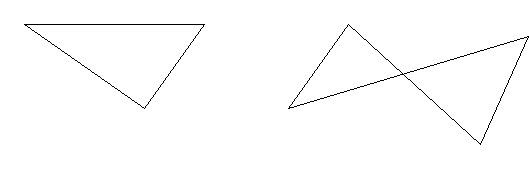
3. Элементы четырёхугольника: вершины, стороны , диагонали.
   

А В



Д С

АВ и СД, АД и ВС – противоположные стороны;

А и С, В и Д – противоположные углы;

А и С, В и Д – противоположные вершины;

АВ и ВС, ВС и СД ит.д. – смежные стороны;
АС и ВД – диагонали.

Определение: Диагональ-отрезок, соединяющий две противоположные вершины.

Вывод: если сравнить элементы четырёхугольника и треугольника, то увидим, что в отличие от треугольника в четырёхугольнике появляются такие понятия как противоположные стороны, углы, вершины, диагональ.

Перед дальнейшим изучением четырёхугольников в их взаимной связи учащимся предлагается построить всевозможные четырёхугольники на доске. Ставится вопрос: «От чего зависит разнообразие форм четырёхугольников?» ( от длин сторон, от взаимного соотношения длин смежных и противоположных сторон, от взаимного расположения противоположных и смежных сторон, величин углов).

4. Рассмотрим пары противоположных сторон. Какими они могут быть? ( параллельными и непараллельными) Построим четырёхугольник с параллельными противоположными сторонами, который называется параллелограммом, и определим его.
   

Параллелограмм – четырёхугольник, у которого противоположные стороны попарно параллельны. А В


Д С

АВСД – параллелограмм, АВ ║ СД, АД ║ ВС.

Вывод: параллелограмм является частным случаем четырёхугольников. ( отмечаем это в родо-видовой схеме)

5. А параллелограммов сколько? (много, зависит это от длин сторон и величин углов) Какими могут быть углы параллелограмма? ( любые).А прямыми ? (да ). Причём если один угол параллелограмма прямой, то и все остальные то же будут прямыми, что следует из свойств параллельных прямых, построим такой параллелограмм, который называется прямоугольником, и определим его.
   

А В



Д С

Прямоугольник – параллелограмм. у которого все углы прямые

Вывод: прямоугольник частный случай параллелограмма (отмечаем это в родо-видовой схеме).

6. Сравним длины смежных сторон параллелограмма. Какими они могут быть? Равными и неравными. Построим параллелограмм с равными сторонами, который называется ромбом.
   

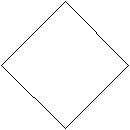А Ромб – параллелограмм, у которого все сто-

роны равны, АВ=ВС=СД =ДА.

Вывод: ромб является частным случаем па-

В Д раллелограмма( отметим это в схеме).

С

7. В прямоугольнике все стороны могут быть равными? (да). Построим такую фигуру, получается квадрат.
   

Квадрат- прямоугольник , у которого все стороны равны. Вывод: квадрат один видов прямоугольника (отметим это в схеме)

А В

А

.

Д С

Определим квадрат через ромб. Квадрат –это ромб, у которого все углы прямые, Вывод: квадрат частный случай ромба(отметим это на схеме).

Итак: мы рассмотрели множество четырёхугольников с попарно параллельными противоположными сторонами, к которым относятся параллелограмм, прямоугольник, квадрат, ромб.

8. Рассмотрим четырёхугольник, у которого две противоположные стороны параллельны . а две другие не параллельны. Построим такую фигуру, которая называется трапеция.
   

Трапеция-четырёхугольник, у которого две стороны параллельны . а две не параллельны.


А В АВСД – трапеция, АВ ║ СД – основания,

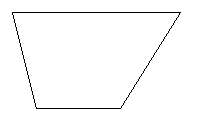АД не параллельна ВС- боковые сторо-

Д С ны

9. Рассмотрим разновидности трапеции. От чего это зависит? (от величины углов и длин боковых сторон) Боковые стороны могут быть равными? (да). Построим такую трапецию, которую называют равнобедренной.
   

А В



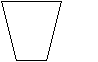
Д С Равнобедренная трапеция- трапеция с равными боковыми сторонами, АД = ВС.

10. Построим трапецию , у которой есть прямой угол. Сколько прямых углов может быть у трапеции? (два).

А В


Д С


Прямоугольная трапеция- трапеция с прямым углом, угол А = 90°.

Отмечаем все виды трапеции в родо-видовой схеме.


Домашнее задание: стр. 11 в. 4-6, 10-12, 14,15. №369, 366.


Первичное закрепление: решение задач №367, 370.( решение проходит в виде беседы)


Итог урока: ( делают учащиеся) итак, мы изучили понятие четырёхугольник, узнали все виды четырёхугольников, составили родо-видовую схему,которая показывает наглядно взаимосвязь между всеми четырёхугольниками. Установили, что многообразие четырёхугольников зависит от взаимного расположения и соотношения его элементов.


Приложение №1

Тема «Равнобедренный треугольник и его свойства»


Задача «На высоте ВВ1 равнобедренного треугольника АВС (АВ =ВС), взята точка Д. Доказать, что 1) тр. АВД = тр. ВДС; 2) тр. АДВ1 = тр. ДВ1С

Рассмотрим разные док-ва второго равенства:


1способ: треуг АДВ1=треуг. ДВ1С, т.к. АД =ДС, ДВ1=ДВ1(общая),угол АДВ1 =уголВ1ДС(смежные с ними углы равны)


2 способ: треуг. АДС равнобедренный, т.к. АД=ДС, ДВ1 – высота, а значит биссектриса угла АДС, тогда треуг.АДВ1 = треуг.ДВ1С по двум сторонам и


3 способ: В треугё АВС ВВ1 – высота, а значит медиана. Следовательно, АВ1= В1С и угол АВ1Д = углу ДВ1С = 90°, а ДВ1 в треуг. АДВ1 и ДВ1С общая. Значит треуг. АДВ1 =треуг.ДВ1С.


4 способ: треуг. АДС – равнобедренный, АД = ДС, ДВ1 – его медиана, значит АВ1= В1С и угол ДАС = углу ДСА как углы при основании равнобедренного треугольника. Значит треуг. АДВ1 = треуг. ДВ1С.


Приложение №2

Тема « Смежные углы»

Проблема №1 Как уравнения помогают решать геометрические задачи?

1.1По рисунку составьте задачу, в которой требовалось найти величины смежных углов. Решите её.


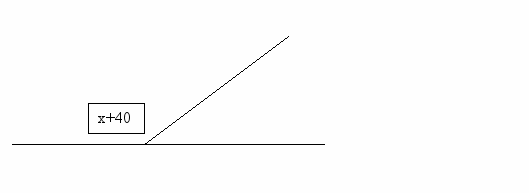
х


1.2Составьте задачу на нахождение величины смежных углов, , которая сводилась бы решению уравнения х + ( х – 20 ) = 180. Решите её.


1.3Составьте задачу на нахождение величины смежных углов, которая сводилась бы к решению уравнения х + 5х = 180. Решите её.


Проблема № 2 Как вычисления подсказывают геометрическую закономерность?

2.1Смежные углы равны α и 180 –α





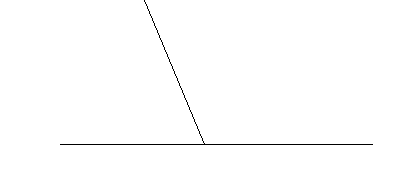
Над этими величинами выполним следующие действия:

1. α/2; (180 – α) / 2
   
2. α/2 + (180 – α) /2 = 90.
   

Получили угол 90°. Что это за угол? Изобразить его на рисунке. Какую геометрическую закономерность вы заметили? Сформулировать её.


2.2 Пусть α и β – смежные углы. Пусть угол α изменяется в границах от 0 до 60. В каких границах изменяется при этом угол β?

Проблема №3 Сколько данных должно быть в задаче?

3.1 Один из смежных углов больше другого на 60 или в 2 раза. Найти эти углы. Нет ли в задаче лишних данных? Составьте задачу без лишних данных. Решите её.

3.2 Один из смежных углов больше другого на 60 или в 3 раза. Найти эти углы. Нет ли в задаче лишних данных? Не противоречат ли они друг другу? Составьте задачу, не имеющую указанных недостатков. Решите её.

3.3 Один из смежных углов больше другого на некоторую величину. Найти эти углы. Хватает ли данных для решения задачи? дополните условие задачи и решите её.


Проблема №4 Всегда ли выручает анализ?

4.1 Один из смежных углов увеличился на 35(уменьшился на 10). Как изменится второй угол?

4.2. Один из смежных углов увеличился в 3 раза( уменьшился в 2 раза). Как изменился второй угол?


Приложение № 3


Тема « Правила вычисления производных, производная сложной функции, производные тригонометрических функций»

1-2 уроки: лекция

План лекции:

1. Повторение определения производной.
   
2. Теорема о дифференцировании суммы двух функций. Образцы решения примеров.
   
3. Правило дифференцирования произведения двух функций.
   
4. Следствие о вынесении постоянного множителя за знак производной. Образцы решения примеров.
   
5. Правило дифференцирования частного двух функций. Образцы решения примеров. Разбор решённых в учебном пособии примеров.
   
6. Формула для нахождения производной степенной функции . разбор примеров, решённых в учебном пособии.
   
7. Понятие сложная функция, область определения сложной функции.
   
8. Производная сложной функции.
   
9. Производные тригонометрических функций.
   

3-8 уроки – уроки практикумы. На каждом из них проводится повторение вопросов теории и опрос учащихся. Ведётся целенаправленная работа по выработке умений и навыков решения задач различного уровня сложности.

9-10 уроки – урок-семинар.

10-11 уроки - контрольная работа (тест)

12-13 уроки – работа над ошибками и решение задач повышенного уровня.

Приложение №6

План урока ( или внеклассного мероприятия):

1. Лекция учителя по плану:
   

• Когда и где возникла геометрия?
  
• Причины возникновения геометрии.
  
• Евклид и его «Начала».
  
• История аксиомы параллельности(v постулат) Евклида и попытки его доказательства учёными разных стран.
  
• Открытие Н.И.Лобачевским и Я.Бойяи неевклидовой геометрии.
  
• Роль неевклидовой геометрии для изучения физики, астрономии и механики.
  

1. Ознакомление учащихся с жизнью и деятельностью Н.И.Лобачевского (сообщения учащихся):
   

• Краткая биография.
  
• Труды Лобачевского по геометрии и его вклад в другие науки.