Geum.ru

Уроках математики посредством сообщения им сведений из истории науки

Вид материалаУрок

Содержание


Тип урока
Тетрадь с печатной основой: (выполняются номера: № 26(а,б) стр.11) Ход урока
Ответ: АВ, ВС, СД, АД
Подобный материал:

Воспитание школьников на уроках математики посредством сообщения им сведений из истории науки


Максименко Ольга Валентиновна — учитель математики


Идеи гуманизации и гуманитаризации математического образования вывели на первый план проблемы, которым ранее не уделялось достаточного внимания. Одной из таких проблем является проблема преподавания истории математики в школе [2]. Появившиеся в литературе за последнее время публикации свидетельствуют о повышении интереса к обозначенной теме. В основном это статьи о методах, способах и приемах использования исторических сведений на уроках математики. Мы же попытаемся раскрыть воспитательный потенциал, которым обладает история науки.

Среди целей преподавания математики в школе можно выделить одну - формирование у учащихся представлений о математике как части общечеловеческой культуры. Учителя математики часто считают ее не главной и не уделяют должного внимания соответствующей работе на уроке. Практика работы с историей математики показывает, что именно при помощи истории науки, которая методически правильно включена в урок, достигается вышеуказанная цель. Например, можно заметить, что история науки дает возможность показать учащимся при изучении каждого нового раздела или темы, что математика как наука о пространственных формах и количественных отношениях реального мира возникала и развивается в связи с практической деятельностью человека. Возьмем возникновение и развитие понятия числа, которое происходило вместе с зарождением и развитием математики. Практическая деятельность с одной стороны, и внутренняя потребность математики с другой стороны, определили развитие понятия числа. Так, например, отрицательные числа вошли в использование как «недостаток», а положительные как «наличие». Такого определения отрицательных чисел придерживался Диофант Александрийский. Р.Декарт же, при рассмотрении координатной плоскости истолковал положительные и отрицательные числа как противолежащие направленные отрезки, т.е. дал им геометрическое истолкование [8]. На самом деле, примеров практической значимости математики для человеческой деятельности можно привести множество, что и следует показать ученикам при помощи истории математики. Такая неразрывная связь истории науки и преподавание темы по математике поможет ученикам осознать, что они изучают науку, которая является частью окружающего нас мира, частью нашей истории.

Аналогично, по мере возникновения насущных задач практики, появлялись не только новые понятия, но и создавались математические методы решения таких задач. Из истории человечества видим, что изобретение самолета потребовало решения задачи движения твердого тела в воздухе. Великий русский ученый Н.Е.Жуковский, применив новые математические методы, решил эту задачу, создав основу математической теории полета [7]. Наблюдения показывают, что ученики 5-9 классов общеобразовательных школ знают в лучшем случае имена Пифагора, Евклида, Виета, теоремы, которых входят в школьный курс математики. Поэтому считаем, что ученики должны знать и такие имена,


как М.И.Остроградский, Н.И.Лобачевский, Н.Е.Жуковский, К.Э.Циолковский, С.Н.Бернштейн, М.В.Келдыш и многих других отечественных ученых. Их имена вошли в историю науки в связи с решением практических задач, имеющих большое значение для развития народного хозяйства, военной техники, развития науки.

Редко кто из учителей математики, использующий на своих уроках сведения из истории науки, задумывался о пользе этих сообщений в плане воспитания школьников. Так, согласно Г.И.Глейзера [4], история математики обладает огромным воспитательным воздействием на подрастающее поколение. Это его утверждение относится ко всей гамме представлений о воспитании: внушение потребности к труду, ответственности за порученное дело, формирование высокой нравственности, развитие научного любопытства, т.е. желание не только приобретать знания, но и преумножать их. Самое главное в том, что история науки приучает, а потом заставляет быть закономерным, самостоятельно добывать знания. Также большое воспитательное воздействие окажет на учеников сообщение об огромной роли А.Н.Крылова, С.А.Колмогорова, Н.Г.Четаева и других в создании и совершенствовании новой военной техники. Так, работы А.Н.Колмогорова во время Второй мировой войны способствовали созданию теории артиллерийской стрельбы. А.Н.Колмогоров изучал явления рассеивания артиллерийских снарядов [7]. Знакомство с биографиями крупных ученых, с методами их работы дает исключительно много для формирования характера учащихся, их идеалов и высоких стремлений, на этом основывается преподавание истории математики у Б.В.Гнеденко [5] Так, при сравнении биографий С.В.Ковалевской и П.Я.Кочиной, школьники увидят два мира, две эпохи, две судьбы. С.В.Ковалевская не была принята в университет, ей не разрешили работать в России, П.Я.Кочина же окончила Ленинградский университет, работала в Академии наук СССР, ей присвоено звание Героя Социалистического труда [7]. Однако вклад обеих женщин-математиков в развитие науки очень велик.

Эстетический потенциал математики в практике обучения часто недооценивают. Однако на протяжении веков пути математики и различных видов искусства переплетались. Поэтому исторические сведения предоставляют благодатный материал для развития эстетического вкуса школьников [9]. Зачастую в кругу цифр и математических знаков мы не замечаем всей красоты и логичности доказательств этой науки. Красоту науки когда-то заметил Н.Е.Жуковский. Он писал: «В математике есть своя красота, как в живописи и в поэзии» [10]. Многие ученые, занимавшиеся исследованиями в области математики, были не только математиками, но физиками и химиками, как Ньютон, Паскаль и Эйлер, и даже поэтами. Философом и поэтом является известный математик Омар Хайям. Вот одно из его четверостиший [9]:

Чтоб мудро жизнь прожить, знать надобно немало.

Два важных правила запомни для начала:

Ты лучше голодай, чем что попало ешь,

И лучше будь один, чем вместе с кем попало.

Другой пример - математик Чарльз Л.Доджсон, известный больше под псевдонимом Льюис Кэрролл как автор сказки «Алиса в стране чудес». Как рассказывают биографы, королева Виктория пришла в восторг от этой книги и захотела прочитать все книги, написанные Кэрроллом. Можно представить ее разочарование, когда она увидела на своем столе стопку книг по математике. И даже известная нам математик-женщина Софья Васильевна Ковалевская обладала незаурядным литературным талантом. Ее перу принадлежат такие произведения: драма «Борьба за счастье», роман «Нигилистка» и другие [9].

Решать уравнение вида: х-ау=1, по-видимому, умел и Архимед, находим мы в книге Н.Я.Виленкина [1]. Недаром Архимед послал в Александрию Эратосфену следующий стихотворный вызов:

Сколько у Солнца быков, найди для меня, чужестранец

( Ты их, подумав, сосчитай, мудрости если не чужд),

Как на полях Тринакрийской Сицилии острова тучных

Их в четырех стадах много когда-то паслось.

Цветом стада различались: блистало много млечно – белым,

Темной морской волны стада другого был цвет.

Рыжим третье было, последнее пестрым. И в каждом

Стаде была самцов множеством тяжкая мощь,

Все же храня соразмерность такую: представь чужестранец,

Белых быков в точности было ровно…

То, что древние математики были прекрасными поэтами, можно видеть из приведенных примеров. Эти произведения помогут показать ученикам красоту не только самой математики, но и поэзии, прозы и других древних сочинений. При этом исторические сведения помогут сосредоточить и сконцентрировать внимание учащихся на изучении программного материала, помогут надолго сохранить в памяти те факты, которые были красиво описаны с помощью литературы.

В стихах, приведенных выше, также встречаются географические названия: Александрия, Тринакрийская Сицилия и другие. При сообщении учащимся исторических сведений, если учитель приведет карты древние и современные, то ученики наиболее полно представят себе картину времени, когда произошло математическое открытие. При рассмотрении карт ученики могут найти древние города, например, город Александрию, и затем ответить на вопросы: каким морем омывается город? (Средиземным); с какой рекой связаны истории этого города?; к какой стране принадлежит Александрия? (Египет); назвать главную реку Египта и ее природные особенности? (Нил); перечислить известных людей, проживавших в Александрии? (Евклид, Эратосфен, Апполоний, Герон, Гиппарх, Птолемей, Диофант). Такая работа позволяет развивать воображение, мышление учащихся и тем более поможет лучше разобраться в географических местах и надолго отложиться в памяти детей, так как эти знания были добыты путем сопоставления карт. Приведенный в примерах Диофант занимался изучением методов решения уравнений. Уравнения, решаемые в целых числах так и назвали Диофантовыми уравнениями. А также с его именем связаны понятия Ал-джебра и Ал-мукабала [1].

Ал-джебра

При решении уравненья,

Если в части одной,

Безразлично какой,

Встретится член отрицательный,

Мы к обеим частям,

С этим членом сличив,

Равный член придадим,

Только с знаком другим,

И найдем результат нам желательный.

 

Ал-мукалаба

Дальше смотрим в уравненье,

Можно ль сделать приведенье,

Если члены в нем подобны,

Сопоставить их удобно,

Вычтя равный член из них,

К одному приводим их.

 

После изучения подобных стихов можно выводить современные методы решения линейных уравнений: перенос слагаемых их одной части уравнения в другую, деление и умножение обеих частей уравнения на одно и то же число.

Исследования Н.Я.Виленкина [1] в области истории науки математики, показывают, что математикой занимались не только профессионалы. Эта наука притягивала внимание многих людей. Так, например, в «Маленьком принце», замечательной сказке французского писателя А.Де Сент-Экзюпери, Лис спрашивает Маленького принца:

- А на той планете есть охотники?

- Нет.

- Как интересно! А куры есть?

- Нет.

- Нет в мире совершенства! - вздыхает Лис.

Н.Я.Виленкин [1] предлагает поспорить о не существовании совершенства в мире и именно с этого литературного текста начать беседу о совершенных числах - числах, делители которых в сумме дают само число.

Опытный учитель с привлечением истории математики к объяснению нового материала сможет показать ученикам значимость математики среди других наук, изучаемых в школе, и их неразрывную связь. Из вышеуказанных примеров видно, что при использовании географических карт, литературных произведений, биографий ученых история математики позволяет установить межпредметные связи, которые очень легко можно проследить на каждом уроке.

При распаде СССР многие социалистические республики, отделившись, стали возвращаться к своим традициям и к родному языку. История математики может вернуть нас к истокам исконно русских открытий, познакомить с нашими отечественными учеными и с их вкладом в становление науки - математики. Известный историк-методист И.Я.Депман справедливо утверждает: «Исторические сведения о математике своей Родины и ее достижениях естественно развивают патриотические чувства и любовь в своей стране, к своему народу. Русская математика, как старая, так и новая, дает для этого очень богатые возможности» [3]. В изучении простых чисел учеников можно познакомить с отечественным ученым П.Л.Чебышевым, которому наравне с другими исследователями этих чисел удалось вывести формулу, позволяющую приближенно найти число простых чисел. Работа по исследованию простых чисел занимала умы ученых около 2200 лет после Евклида, и своим открытием П.Л.Чебышев прославил русскую науку.

Воспитание нравственности у подростков происходит под воздействием взаимоотношений людей, окружающих школьника, его сверстников, людей старшего и предшествующих поколений. Педагогический процесс всегда связан не только с учителями, но и с «явно не присутствующими учителями». В качестве авторитетных «отсутствующих учителей» успешно выступают различные выдающие личности, деятели науки и культуры, в том числе и ученые-математики. Исторический материал, действуя на сознание, на чувства и помыслы школьников, формирует их нравственные идеалы. Поэтому исторический материал обладает огромным потенциалом для патриотического и интернационального воспитания школьников. В интернациональном воспитании, в формировании уважения к народам нашей страны, видим у К.Г.Кожабаева, большое значение имеет ознакомление учащихся с достижениями великий ученых народов СССР, таких, как Хорезми, Омар Хайям, Насирэддин Туси, Гиясэддин Каши и других [7].

Неожиданные открытия, обнаруженные математиками, удивляли многие столетия людей своей красотой и вдохновляли на новые исследования. Говоря словами Г.В.Лейбница, «нет ничего более важного, как обнаружить источники нового открытия. Это, на мой взгляд, интереснее самих открытий». Мы еще раз убеждаемся в ценности элементов истории математики для развития учащихся [3]. В этом случае учитель вместе с учениками может рассматривать новый материал, как никому раннее неизвестный, тем самым происходит новое открытие на уровне каждого ученика в отдельности.

Каждый год видим такую картину: от класса к классу интерес к изучению предмета математики у учащихся не возрастает, как хотелось бы, а наоборот, уменьшается, что влечет за собой и ухудшение успеваемости. Кроме воспитательного значения исторических сведений, учителя математики подчеркивают, что история математики повышает интерес учащихся к предмету, к изучению все новых и новых, усложняющихся тем программы. О развитии интереса к предмету при помощи истории математики говорить нужно много и основательно, поэтому мы не затронем в этой статье возникшей новой проблемы.

Из наблюдений за преподаванием истории математики в школе видим, что наиболее часто применяемыми методическими приемами сообщения исторических сведений являются следующие: рассказ учителя, эвристическая беседа, проблемное изложение, лекция, исследовательская работа учеников. Мы выделяем еще один прием, который заключается в решении той или иной задачи различными методами, не исключая существовавших ранее, может быть даже и ошибочных. А также прием выполнения одного математического действия различным образом. Например, при изучении темы умножения десятичных или обыкновенных дробей школьникам в 6 классе можно показать приемы умножения дробей старорусским и другими способами. Н.Н.Круликовский отмечает, что эффективным методом сообщения исторических сведений по математике может быть решение задач из классических и старинных сборников задач [3]. При изучении признаков деления на 2, 3, 5, 10 и т.д. можно показать ученикам признак Паскаля. Затем можно будет сказать, что признаки делимости чисел на 2, 3, 5 и 10 – это частные случаи признака Паскаля.

Согласно Н.Н.Круликовскому, считаем, что ознакомление учащихся с элементами истории математики с целью воспитания должно проходить, прежде всего, на уроках математики [3]. Многолетний опыт исследования данной темы показывает, что освещать историю математики даже в самом кратком виде не предоставляется возможным. Поэтому будем говорить только о сообщении учащимся лишь некоторых сведений из истории науки. Из нестандартным форм сообщения исторических ведений науки математики Н.Я.Виленкин выделяет уроки истории математики, которые проводятся в конце изучения каждой темы. Материал к этим урокам он располагает в учебнике в конце разделов [6].

Мы вводим в практику нетрадиционный прием сообщения сведений из истории математики – нетрадиционные домашние исследовательские задания. Почти исчезли из обихода русские старинные названия мер длины и веса. Ученики на лето обычно из крупных городов разъезжаются к родственникам, бабушкам и дедушкам, которые живут в деревнях, поселках и просто маленьких городках. Из их обихода эти устаревшие слова еще не вышли. За лето ученики могут выполнить специальное задание - составить словарь по старинным мерам длины по рассказам бабушек и дедушек. А во время урока по теме « Измерение отрезков» могут поделиться с остальными своими словарями и позабавить одноклассников различными интересными названиями, такими как сажень, вершок, аршин. Учитель в этом случае подтвердит сказанное школьниками и расскажет, чему в настоящее время равны эти величины. Интересно будет измерить кабинет математики пядями, локтями и шагами. А также исторический материал может стать индивидуальным средством обучения школьников математике.

Историю математики вводить в школу необходимо по нескольким причинам: это прекрасный и действенный инструмент для повышения интереса учащихся к предмету, развития эстетического вкуса учеников, а также привития нравственных качеств. Говоря словами Г.В.Лейбница, «кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет» [10], убеждаемся в этом еще раз. Главное, чтобы исторические сведения гармонично вписывались в современный урок - урок XXI века. XXI век - это век телевидения, компьютеров и компьютерных сетей. На первый план выходит научно-исследовательская деятельность учеников, которая должна привить им навыки самообразования.

Список литературы:
  1. Виленкин Н.Я. За страницами учебника математики 10-11 класс. Москва, Просвещение, 1996
  2. Вопросы организации творческой деятельности учащихся в процессе изучения математики: Методические рекомендации и дидактические материалы/ Под.ред. И.Н. Семеновой. УрГПУ,Е, 2000
  3. Воспитание учащихся при обучении математике. /Составитель Пичурин Л.Ф., Москва, Просвещение, 1987
  4. Глейзер Г.И. История математики в школе VII-VIII классы. Москва, Просвещение, 1982
  5. Гнеденко Б.В. Формирование мировоззрения учащихся в процессе обучения математике. Москва, Просвещение, 1990
  6. Жохов В.И. Преподавание математики в 5 и 6 классах: Методические рекомендации к учебникам Виленкина Н.Я и др.-М.:Русское слово, 1999, С 20.
  7. Кожабаев К.Г. О воспитательной направленности обучения математик в школе: Кн. Для учителя.-М.:Просвещение, 1988
  8. Мясникова Т. История развития понятия отрицательного числа.//Математика в школе №41, 2001, С.29-32.
  9. Савина О.А. Эстетический потенциал истории математики.//Математика в школе №3, 2001, С.69-72.
  10. Шейнина О.С., Соловьева Г.М. Математика. Занятия школьного кружка. 5-6 класс.- М.: Изд-во НЦ ЭНАС, 2002



Урок геометрии на тему «Измерение отрезков» 7 класс.

Цели: 1. Повторить понятие «отрезок»

2. Ввести понятие «измерение отрезков», «длина отрезка».

3.Научить находить длину отрезка по данным длинам отрезков его составляющих и находить длину отрезка по данной длине большего отрезка и каких-то его частей.

4. Развивать: логическое мышление; внимание; внимательность; зрительную и слуховую память; интерес к изучаемому материалу; к предмету; самостоятельную деятельность; активность.

5. Воспитывать: уважительное отношение к ответам учеников, умение высказывать свое мнение, умение логично выстраивать свои ответы.

Тип урока: комбинированный.

Наглядные пособия: иллюстрации мер длины, чертежи к задачам, видеозапись мультфильма, учебник, тетрадь с печатной основой, тетрадь рабочая.

Оборудование: доска, графопроектор, телевизор, видеомагнитофон, доска для работы за партой.

Учебник по которому ведется обучение: Л.С. атанасян Геометрия 7-9 класс. М.: Дрофа, 1999-2003г. (выполняются номера: рисунок 25 стр.24, №2 стр.25, Д/З:№ 8(а), №10(а) стр.27 )

Тетрадь с печатной основой: (выполняются номера: № 26(а,б) стр.11)

Ход урока:

«Нет ничего более важного, как обнаружить источники нового открытия. Это, на мой взгляд, интереснее самих открытий»

Г.Лейбниц.

1. Мотивация

В повседневной жизни нам постоянно приходиться что-то измерять, мерить. Приведите примеры ваших измерений (ученики: ткань, комнату, доску, фанеру и т.д.)/

А как вы думаете, какова длинна нашего кабинета, в метрах, на глаз? Каждый высказывает свое мнение.


2.Постановка целей и задач

Сегодня на уроке мы с вами узнаем, что значит измерить отрезок и как найти длины различных отрезков


3.Повторение

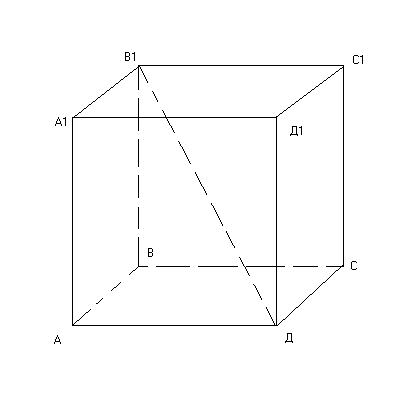
Но прежде, чем измерять отрезки мы вспомним, что такое отрезок и все что с ним связано. Учитель приглашает одного ученика к доске, чтобы он рассказал теорию про отрезок. А остальные работают в тетради. Задание: выпишете все имеющиеся отрезки на чертеже.

Ответ: АВ, ВС, СД, АД,

А1В1 ,В1С1, С1Д1, А1Д1,

АА1, ВВ1,СС1, ДД1, В1Д.

Отвечающий у доски должен рассказать определение отрезка (отрезок – это часть прямой, ограниченная двумя точками). Проверка задания происходит в парах, поменявшись тетрадями (если задание выполнено верно, то поставьте на полях «+», если 4-5 ошибок, то «+», «-» , и если более 5 ошибок, то «-»). Здесь необходимо еще раз упомянуть, что АВ и ВА – это название одного итого же отрезка.

Проверяем задание у доски про отрезок.


4. Новый материал

Пусть сегодня отрезком будет наш кабинет. Будем его измерять. Но как это сделать?

Мы будем измерять кабинет шагами, линейкой и т. д. (дети меряют кабинет тем, чем предложили). Получили все результаты измерения разные.

Тогда может нам подскажут герои мультфильма как измерить кабинет? (смотрим мультфильм «38 попугаев» в приложении № 2)


Мы увидели, что рост удава: 5 мартышек, 2 слоненка,38 попугаев.

Опять все результаты получились разные. Давайте заглянем в учебник, может там найдем объяснение. Опишите рисунок в учебнике.

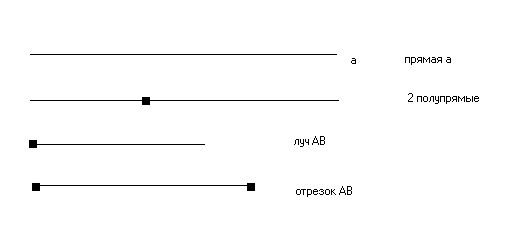
- Что бы измерить отрезок АВ, сначала выбрали единицу длины и затем эта единица длины укладывается в отрезок несколько раз. Остается еще часть отрезка. Тогда единицу длины делят на доли, в данном случае на 10. Оставшаяся часть отрезка совпадает с 4 такими долями. Итого, отрезок АВ=2,4 единицы длины.

Таким образом, что значит измерить отрезок? (Ответ: значит, выбрать единицу длины и сравнить отрезок с ней).

Человек в своей жизни не раз проводит какие-то измерения, простые и сложные. Для первобытного человека строившего себе жилище, изготовлявшего орудия труда, посуду применение мер длины было необходимо.

Первыми образцами мер длины для первобытного человека послужили части тела: руки, ноги, пальцы.

Небольшие расстояния мы до сих пор меряем шагами, ладонью, пядями.

Длину веревки или ткани удобнее мерить локтями, саженями, косыми саженями, маховыми саженями (показывает презентацию «Меры длины» в приложении № 3)


Раз мерки у нас есть, то давайте попробуем ими измерить кабинет (измеряют: 1ряд-шагами, 2ряд-локтями, 3ряд- ладонями)

Что получилось? -8шагов, 17 локтей, 32ладони.

Опять получили разные ответы. (в кабинет входит переодетый ученик). Давайте послушаем этого человека. Кто вы?

- Я, Менделев Дмитрий Иванович, в 1867 году предложил на съезде русских естествоиспытателей, что в России необходимо ввести единую метрическую систему.

И в 1872 году комиссия в Париже утвердила эталон метра. Он состоит их 90% платины и 10% иридия, в виде стержня, с поперечным разрезом в виде буквы «X», и составляет одну сорока милионную часть меридиана.


Вот теперь все стало ясно. Будем измерять кабинет метрами. В тетрадях - сантиметрами и миллиметрами, на местности - километрами.

Для измерения расстояний существует специальный прибор-линейка, на которую уже нанесены деления.


5. Закрепление нового материала.

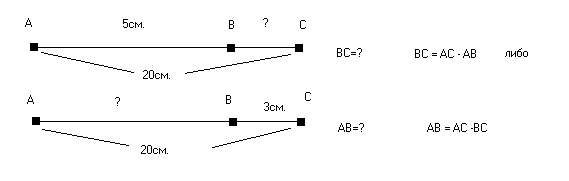
Решите задачу по чертежу:

Что нужно сделать, чтобы найти длину отрезка АС?

- Необходимо к длине отрезка АВ прибавить длину отрезка ВС. (АС=АВ+ВС)

Теперь составьте задачу, обратную данной.




(если ученики правильно выполнили задание, то они поставят себе карандашом на полях «+»)


Далее идет работа группами. Ученики работают самостоятельно: например, 3 ряд выполняет задание в тетради, затем идет проверка на графопроекторе.

З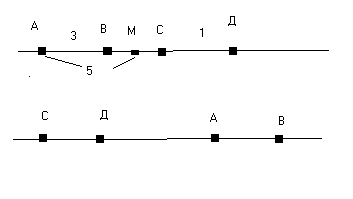адание: Какая точка лежит между двумя другими, если точки А, В, С лежат на одной прямой и АВ=1,5, ВС=4, АС=2,5.


А 1 и 2 ряд работают у доски. Решаем задачу из тетради с печатной основой:

АВ= 3, СД = 1, АС = 5. Чему равно расстояние между серединами отрезков АД и ВС? (ответ: а) 1, б) 0).


Затем ученики самостоятельно выполняют второе здание этого номера.

Третий ряд проверяет правильность выполнения задания с помощью графопроектора.



(если ученики правильно решили задачи, то ставят себе на полях карандашом «+»).


Теперь мы знаем, как измерить длину отрезка. А кабинет до сих пор не измерили.

Давайте сверим, правильно ли вы в начале урока определили длину кабинета на глаз. Молодцы, глазомер у вас хорошо развит (кто- то метровой линейкой измеряет кабинет).

6. Подведение итогов.

Ученики по очереди перечисляют, что они на уроке изучили нового. Затем учитель выставляет оценки за урок: решавшим у доски, отвечающим с места, а те, кто набрал по 3 «+», то записывает себе фамилии.