Задачи: провести диагностическое исследование уровня развития творческого мышления младших школьников; введение приемов и методов работы направленной на развитие творческого мышления школьников на уроках математики

Вид материала

Содержание

Школьному курсу геометрии
Домашняя работа учащихся
Дополнительные задания
Внеклассное занятие: «Увлекательный КВМ»
II. Кто больше ответит за минуту (табличное умножение и деление)
III. Реши примеры “Замени число буквой”
IV. Конкурс капитанов (с кубиками).
V. Задача на смекалку (командам даются лодочки – надо перевезти ведущего)
VI. Игра “Телефон”

Подобный материал:

Тема:

«Развитие творческого мышления младших школьников на уроках математики через самостоятельную работу».

Турбина М. М., учитель начальных классов.

Технология опыта

Цель опыта – обеспечение положительной динамики творческого мышления в учебно-воспитательном процессе на уроках математике через самостоятельную работу.

Реализации поставленной цели способствуют следующие задачи:

- провести диагностическое исследование уровня развития творческого мышления младших школьников;

- введение приемов и методов работы направленной на развитие творческого мышления школьников на уроках математики;

- создание условий для использования разного вида самостоятельной работы с целью развития творческого мышления.

Самостоятельная работа дает положительные результаты, помогает учащимся усвоить знания и приобрести умения, способствует развитию их способностей. Учитель использует следующие виды самостоятельной работы: самостоятельная работа по образцу; творческая самостоятельная работа; вариативная самостоятельная работа; конструктивная самостоятельная работа.

Творческую самостоятельную работу можно использовать при закреплении, при составлении задач, уравнений, схем, графиков; при объяснении нового материала. Вариативную самостоятельную работу можно использовать при решении задач разными способами, нахождении значения выражений удобными способами. Самостоятельную работу по образцу - при составлении плана решения задачи, таблицы к задачам на нахождение расстояния, скорости, времени движения, или с величинами. Очень важно предлагать ребятам самостоятельную работу для решения задач логического характера, составление магических квадратов, цепочек, задач-смекалок.

Самостоятельная работа учащихся должна входить органической частью во все звенья процесса обучения. Она будет достаточно эффективной как в отношении усвоения учащимися знаний, так и в отношении их способностей, если будет организована в системе уроков. Способы дифференциации, которые могут быть использованы на уроках математики на этапе закрепления изученного материала предполагают дифференциацию содержания учебных заданий:

по уровню творчества;
трудности, объему;
степени самостоятельности учащихся;
характеру помощи учащимся;
форме учебных действий.

Способы дифференциации могут сочетаться друг с другом, а задания могут предлагаться ученикам на выбор. Дифференциация учебных задании по уровню творчества. Такой способ предполагает различия в характере познавательной деятельности школьников, которая может быть репродуктивной или продуктивной (творческой).

Дифференцированная работа при организации самостоятельной работы организуется различным образом. Чаще всего учащимся с низким уровнем обучаемости (1-я группа) предлагаются репродуктивные задания, а ученикам со средним (2-я группа) и высоким (3-я группа) уровнем обучаемости творческие задания. Можно предложить продуктивные задания всем ученикам. Но при этом детям с низким уровнем обучаемости даются задания с элементами творчества, в которых нужно применить знания в измененной ситуации, а остальным - творческие задания на применение знаний в новой ситуации.

Для выработки навыка сложения, вычитания, умножения и деления широко используются пособия «Ромашка» и «Лабиринт», которые позволяют экономить время на уроке и составлять любые примеры на все арифметические действия. Указкой показывается на соответствующий знак и число, а учащиеся записывают ответ.

По данным пособиям проверяются знание учащимися таблицы умножения и деления, внетабличного умножения и деления, составляются примеры на сложение и вычитание чисел в пределах сотни, тысячи, на увеличение числа в 10, 100, 1000 раз, практикуется счет десятками, сотнями и т.д.

Эти пособия не только оживляют урок, но и дают возможность составлять много самых разнообразных примеров на все арифметические действия, которые каждый ученик решает самостоятельно.

Содержание учебной программы, раннее введение математических терминов позволяет с 1 класса развивать мышление учащихся, что способствует самостоятельной мыслительной деятельности учащихся.

В практике обучения детей математике заметно большее влечение детей к текстовым задачам, нежели к вычислительным примерам. И это неудивительно: в задаче, как правило, интерпретируется некоторая реальная ситуация, близкая пониманию детей, явно выражена связь с практикой.

Вычислительные примеры представляются детям весьма абстрактными, лишенными практической цели, а работа над ними – скучным занятием. Между тем именно вычислительные примеры являются основным средством формирования умений и навыков выполнять вычисления, без чего немыслимо овладение основами наук, а также почти любым видом практической и профессиональной деятельности.

Изучая такие темы, необходимо найти какой-то иной подход, прием объяснения нового материала и уже хорошо изученного, прием, который способствовал бы активизации деятельности учащихся на уроке, развитию их интереса к математике, развитию творческого мышления.

Во время изучения данной темы «Сложение и вычитание в пределах 10» на доске, как правило, есть числовой ряд чисел. Дополняя его стрелками и знаками действий - заставляем этот ряд чисел «говорить».

+1 +1 +1 +1 +1 +1 +1 +1

1 2 3 4 5 6 7 8 9

-1 -1 -1 -1 -1 -1 -1 -1

По такому ряду все, даже самые слабые ученики, решают примеры на сложение и вычитание с числом 1 самостоятельно.

А как же решать примеры вида ± 2, ±3, ±4, ± 5? Для решения примеров данного вида, совместно с детьми, составляются новые числовые ряды.

Постоянная работа над ними приводит к успеху даже самых слабоуспевающих. Практика показывает, что уровень самостоятельности при выполнении заданий различен. Зависит он не только от степени овладения учащимися знаниями, умениями и навыками, но и приемами самоконтроля

Таким образом, учащиеся не только закрепляют и совершенствуют вычислительные навыки, но и учатся творчески мыслить, наблюдать, логически рассуждать, делать самостоятельные выводы.

К

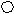
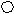
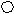
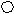
заданиям творческого характера относится и решение задач-шуток. Например, предлагается учащимся такую задачу-шутку: «8 сторожей охраняли снаружи большой склад с горючим материалом. Сторожа были расставлены так, как изображено кружками на чертеже.

Затем пришло распоряжение: охрану склада усилить, поставить у каждой стороны по три сторожа, однако новых сторожей не нанимать. Как надо расставить сторожей, чтобы выполнить распоряжение?»

О

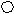
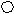
твет: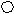

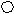
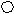
Эта задача является новой для ученика, а для ее решения необходимо найти новый способ.

Такая организация самостоятельной работы помогает сильному ученику проявить свои творческие способности, а слабому дает возможность познать радость труда, найти правильный путь решения, используя дифференцированную помощь.

Так как в классе не только способные к математике учащиеся, используются приемы дозированной помощи, когда для решения основной задачи ребенку предлагается задача-подсказка.

В этом случае дифференциация обучения происходит не по принципу больше – меньше, а по принципу труднее – легче. Это дает возможность каждому ребенку решить любую задачу в разные периоды обучения.

Школьному курсу геометрии отводится важная роль в развитии учащихся – научить их логическому мышлению, развить пространственное представление. Для достижения достаточного уровня пространственных представлений и самостоятельности мышления учащихся имеются не использованные пока возможности. Эти возможности учитель видит в совершенствовании обучения геометрии с помощью включения в процесс 1-4 классов специальных заданий различной степени трудности, учитывающих разные уровни развития детей.

Нестандартные индивидуально-дифференцированные задания, направленные на развитие восприятия, воображения, памяти и мышления позволяют учащимся в полной мере проявить способности, развить инициативу, самостоятельность, творческий потенциал.

Домашняя работа учащихся – это особый вид самостоятельной работы. Он проходит без непосредственного руководства учителя, поэтому нуждается в создании необходимых условий для его выполнения.

Как бы хорошо не проводились уроки, они одни не могут обеспечить навыка самостоятельной работы. Этот навык формируется при правильной организации работы по выполнению домашнего задания и при тщательном контроле за его выполнением.

Как показали наблюдения, домашняя работа учащихся протекает особенно эффективно лишь тогда, когда организована оперативная помощь со стороны учителя, не сковывающая инициативу и самостоятельность учеников. Руководство и помощь в процессе выполнения учащимися домашнего задания осуществляю не только непосредственно в контакте учителя и ученика, но и опосредовано через дифференцированные задания. Непременно учитываются и недостатки в развитии отдельных учеников: неустойчивое внимание, замедленный темп работы, уровень развития речи, логического мышления и др.

Дифференциация домашнего задания требует вдумчивой, кропотливой работы, творческой подготовки к каждому уроку и хорошего знания индивидуальных способностей учеников.

Обучение детей решению задач требует творческого отношения. Планируя урок, тщательно продумывается весь процесс самостоятельного решения задачи: заранее намечаю вопросы для слабых учащихся и дополнительный материал к задаче сильным ученикам. Одни учащиеся способны видеть разные способы решения, другим необходима значительная помощь для того, чтобы просто задачу решить. Да и потребность в мере помощи различна у разных учеников.

На этапе закрепления знаний, умений и навыков проводится дифференцированная работа с использованием дополнительных заданий. Дополнительные задания должны быть точно сформулированы и посильны детям для самостоятельного решения. Их заранее записываю на доске, таблице. Дополнительные задания одновременно предлагаю всем учащимся класса. Но к ним каждый приступает только тогда, когда выполнит основное задание. Как правило, их успевают выполнить дети с хорошим умственным развитием. Дополнительных заданий к задаче можно составить одно, два или три в зависимости от цели урока, трудности заданий, наличия времени на уроке для выполнения самостоятельной работы.

Приведу пример дополнительных заданий к задаче для учащихся 4 класса.

Основное задание: «Длина школьного сада прямоугольной формы 75 м, а ширина – 40 м. 1/5 площади сада занимают ягодные кусты, а остальную площадь – яблони. Сколько квадратных метров занято яблонями?»

Дополнительные задания:

Используя результаты решения задачи, вычисли: сколько ягодных кустов и сколько яблонь посажено в школьном саду, если на каждый куст требуется 3 м², а на каждую яблоню 16 м²площади сада?
Используя результат решения второй задачи, вычисли: сколько килограммов яблок собрали в саду, если с каждой яблони собирали в среднем по 52 кг яблок? Сколько ягод собрали в саду, если с каждого куста в среднем собирают по 6 кг ягод?

Важно, чтобы основное задание решили все учащиеся класса. Выполнение дополнительных заданий рассчитано на детей, которые раньше других справятся с основным заданием. После чтения основного задания в классе найдутся дети, способные его выполнить самостоятельно. С оставшимися учениками, продолжается работа над поиском решения задачи. После повторного чтения задачи снова найдутся дети, способные решить ее. Дается и им такую возможность. Аналогично подводится к самостоятельной работе группа детей после составления краткой записи. Остается часть учащихся, которые не могут приступить к решению задачи. Поэтому снова ведется разбор. Составляется план решения задачи, оказывается помощь. Затем дается время для самостоятельной работы и этой части детей. Детям со слабыми умственными способностями предлагаются карточки индивидуальной помощи. Составляя их, учитываются пробелы в знаниях и возможные затруднения каждого ученика.

Слабоуспевающие дети, используя подобные карточки, решают задачи и могут самостоятельно объяснить ход решения и обосновать выполнение действия. Таким образом, все дети работают над основным заданием, а те, кто его выполнил, сразу приступают к выполнению дополнительных заданий. В это время имеется возможность проследить за ходом самостоятельной работы, оказать помощь отдельным ученикам. Когда все дети справятся с основным заданием, начинается проверка. Выполнение основного задания, как правило, объясняет слабоуспевающий ученик. Объяснение решения дополнительных заданий поручается тем ученикам, которые выполнили их правильно, рационально. При работе над задачей описанным методом каждый ученик работает самостоятельно в меру своих возможностей. Кроме того, в ходе такой работы учащиеся получают дополнительную информацию, проявляют элементы творчества. Рассмотрение разных способов выполнения основного задания, а также некоторых дополнительных заданий сильными учениками, обогащает и остальных, так как показывает новые подходы к проблеме, новые способы ее разрешения. Возникает естественное желание – самостоятельно и наиболее рационально выполнить все предложенные задания. Предлагая детям подобные задания, необходимо добиваться того, чтобы ученик, решая задачу, не просто ответил на вопрос, но умел бы подойти к ней как к проблеме, которую надо рассмотреть со всех сторон. Ведь решение большинства практических задач, с которыми учащиеся могут столкнуться в жизни, имеет различные способы решения, и к этому детей необходимо готовить. Решение задач разными способами развивает математическое мышление, способности к исследованию, творчеству, познавательный интерес и желание учиться.

Так как школа работает по технологии проблемного обучения, то и уроки контроля предполагают организацию самостоятельной деятельности ученика в соответствии со следующей структурой:

- написание учащимися варианта самостоятельной работы;

- сопоставление с эталоном выполнения этой работы;

- оценка учащимися результата сопоставления в соответствии с ранее установленными критериями.

Пример выполнения самостоятельной работы по теме «Деление с остатком» и ее самопроверку по эталону.

Самостоятельная работа:

1. Найди частное и остаток

10 : 3 ; 18 : 5; 42 : 5; 32 : 37

2. Число разделили на 6. Напиши, какие остатки могут быть.

3. Реши задачу.

На одно платье идет 3 метра ткани. Сколько платьев можно сшить из 17 метров ткани?

Дети выполняют работу. Им предлагается эталон, по которому проходит проверка. Задания, в которых допущены ошибки, выписываются отдельно и формулируется проблема: « Почему в данных заданиях допущена ошибка?» Выясняем что, кто - то забыл таблицу умножения, кто-то не помнит алгоритм действия деления с остатком, а кто-то был невнимателен. Мы повторяем алгоритм действия деления с остатком, а на следующий день даю подобную самостоятельную работу и, как правило, ошибок практически нет.

Большую роль в развитии творческого мышления играет и внеклассная работа по математике.

Внеурочные занятия по математике призваны решить целый комплекс задач по углубленному математическому образованию, всестороннему развитию индивидуальных способностей школьников и максимальному удовлетворению их интересов и потребностей.

Внеурочные занятия с учащимися с успехом могут быть использованы для углубления знаний учащихся в области программного материала, развития их логического и творческого мышления, исследовательских навыков, смекалки, привития вкуса к чтению математической литературы, для сообщения учащимся полезных сведений из истории математики.

Чтобы успешно проводить внеклассную работу, учителю приходится постоянно расширять свои познания по математике, следить за новостями математической науки. Это благотворно сказывается и на качестве его. Автор опыта предлагает ряд заданий, которые могут использоваться во внеклассной работе по математике. Этот разнообразный методический материал поможет учителю сделать время пребывания в школе более интересным и содержательным, а также поможет реализовать свои задатки детям с высоким и средним уровнем творческого мышления.

Главная особенность предлагаемого опыта – его направленность не только на то, чтобы дать детям числовую грамотность, но и, в первую очередь, на то, чтобы, используя изучаемый математический материал, создать условия для развития и совершенствования всех познавательных интересов у младших школьников, от класса к классу усиливая акцент на развитие их творческого мышления.

Внеклассное занятие: «Увлекательный КВМ»

Цели: через занимательные упражнения содействовать поднятию интереса детей к математике, расширению их кругозора, развития математических способностей, творческое мышление и воображение.

Оборудование: Ребусы, кубики трех цветов: красный, зеленый, синий; геометрические фигуры: треугольник, квадрат.

Ведущий: Внимание! Внимание! Приглашаю всех отправиться в “царство Математики”. Не забудьте взять с собой быстроту мыслей, находчивость, смекалку, сообразительность, взаимопомощь.

Сегодня в клубе веселых математиков встречаются две команды: команда “Треугольник” и команда “Квадрат”, встречу судят… (состав жюри).

Вам, конечно, хочется знать, чем будете заниматься сегодня. Тогда сумейте открыть вот эти таинственные “двери”. Чтобы их открыть, надо прочитать загаданные слова, которые на них написаны. Это – ребусы. Для каждой команды своя “дверь” и еще одна для болельщиков.

Отгадав ребусы – открывают дверь.

Отгадывать вы уже начали.

I. А сейчас “Разминка”

( Во время разминки команды поочередно отвечают на вопросы, на обдумывание – 30 сек.)

Сколько концов у палки? А у двух с половиной палок?
Если у стола отпилить один угол, то сколько углов останется?
Две сардельки варятся шесть минут. Сколько времени будет вариться восемь таких сарделек?
Шла бабка в Москву и повстречала трех мужиков. Каждый из них нес по мешку, в каждом мешке – по коту. Сколько существ направлялось в Москву?
Пять лампочек тускло горели в люстре. Хлопнули двери – и две перегорели. Сделать нужно вам малость: сказать, сколько ламп осталось.
в клетке находились четыре кролика. Четверо ребят купили по одному из этих кроликов, и один остался в клетке. Как это могло случиться?
Дополни буквы и прочитай написанную фразу:

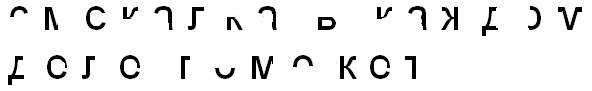
(это будет ваш девиз)

Пока команды выполняют задание, болельщики разгадывают ребусы.

II. Кто больше ответит за минуту (табличное умножение и деление)

14:2	16:8	21:3	24:8	63:7	7*8	9*9	3*9	7*3	5*5
54:6	48:8	45:9	28:7	35:7	9*4	8*6	4*8	2*6	4*5
20:5	25:5	15:3	8:4	81:9	8*8	4*4	2*9	4*6	9*8
72:8	36:6	14:7	56:8	42:7	4*9	7*9	6*5	8*4	9*5
40:5	18:3	63:9	40:8	64:8	18:9	8*7	5*8	6*9	7*6

III. Реши примеры “Замени число буквой”

36:6	54:9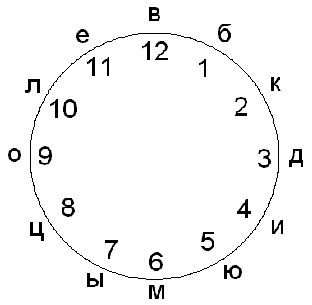
3*3	18:2
2*5	5*2
72:8	81:9
24:8	21:7
2*4	16:2
63:9	49:7

IV. Конкурс капитанов (с кубиками).

Построй башню так:

Красный кубик был выше синего, а зеленый между ними.
Зеленый кубик был не нижний и не верхний, а синий выше красного.
Синий кубик был в середине, а красный ниже зеленого.

Положи кубики в ряд:

Синий кубик был между красным и зеленым, красный слева от синего.
Красный кубик был правее синего, а зеленый между ними.
Зеленый кубик был в середине, а красный слева от него.

V. Задача на смекалку (командам даются лодочки – надо перевезти ведущего)

Ведущему надо переправиться через реку. В лодке мало места, она может выдержать на воде только одного взрослого или двух мальчиков. Как быть? Помогите.

(дети переезжают на другой берег, один остается на берегу, второй возвращается, дает лодку ведущему, он переезжает, а тот, кто был на берегу – возвращается к своему другу)

VI. Игра “Телефон”

Команда (шесть человек) становится в шеренгу.

Сначала проверяется “телефон” первой команды.

Для этого представитель второй команды подходит к крайнему ученику первой команды и тихо диктует первый пример (48:8). Крайний ученик про себя находит ответ и шепотом этот ответ передает рядом стоящему ученику. Представитель второй команды второму ученику сразу же говорит вслух “Прибавь 12 и ответ тихо передай следующему”. Третьему ученику он говорит вслух “Умножь на 4, а ответ тихо передай следующему” и так до конца цепочки. (Затем задание говорит игрок первой команды).

48:8	8*3
+12	:4
*4	+34
:3	*2
-8	-36
*5	:11
Отв. 80	Отв. 4