Geum.ru

Курс специальности «Математика», 7 семестр, 2011-2012 уч г., Одо требования к зачету по дисциплине 1

Вид материалаКонтрольная работа

Содержание


Примерная тематика докладов и рефератов по дисциплине
Подобный материал:
Рассмотрено и утверждено

на заседании кафедры математики, ТиМОМ

протокол № 4 от 28.11.2011 г.

зав. кафедрой _________________ Шебанова Л.П.


Вопросы к зачёту по дисциплине «Избранные вопросы теории групп» (курсы по выбору)

4 курс специальности «Математика»,

7 семестр, 2011-2012 уч. г., ОДО


ТРЕБОВАНИЯ К ЗАЧЕТУ ПО ДИСЦИПЛИНЕ

1. Не иметь долгов по контрольным и самостоятельным работам, выступить на одном из занятий с докладом по предложенной в приложении III тематике.

2. Знать основные понятия и утверждения изученной теории, иллюстрировать их примерами.


Контрольная работа №1 по дисциплине

Вариант №1

1. Является ли группой <А = {a + b }, +>?

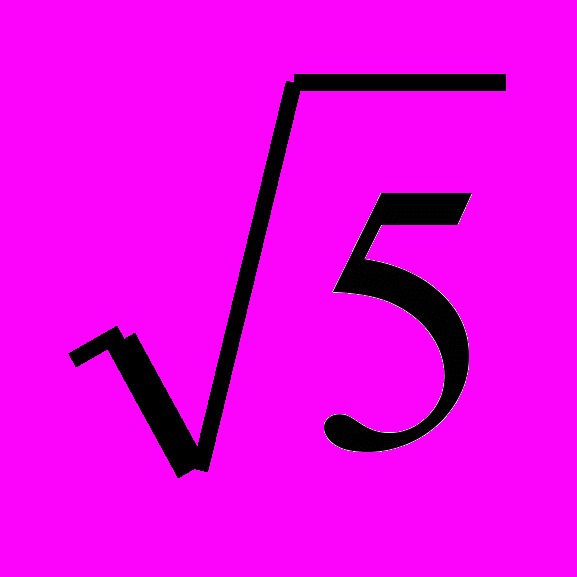2. Образует ли подмножество H = {7k, kÎZ} подгруппу группы ?

3. Построить фактор-группу аддитивной группы 3Z по подгруппе 9Z?

4. Найти левое и правое разложение симметрической группы подстановок S3 по циклической подгруппе, порождённой подстановкой f = .

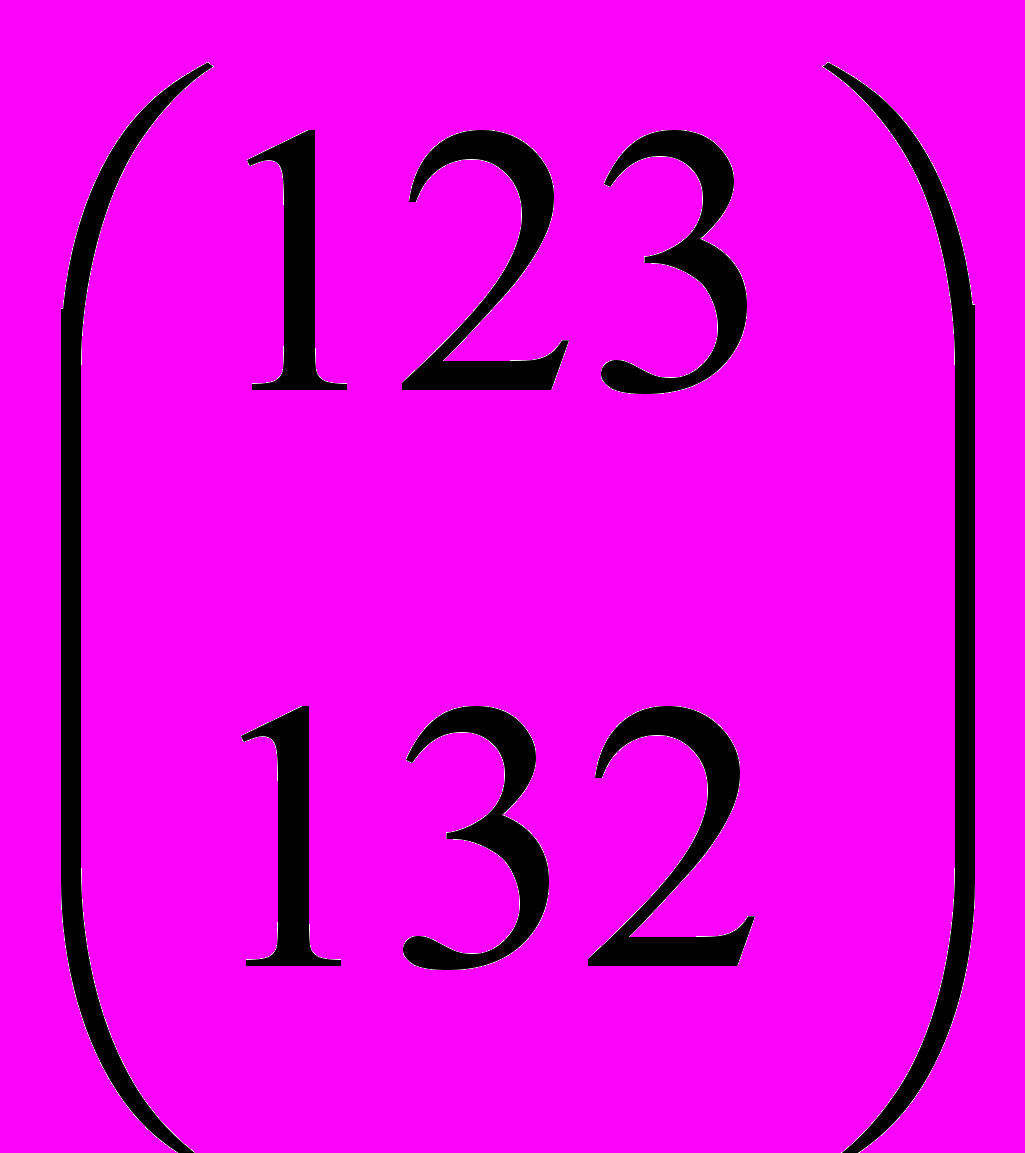5. Доказать изоморфизм групп и <7Z, +>.

Вариант №2

1. Является ли группой <А = {a + b }, +>?

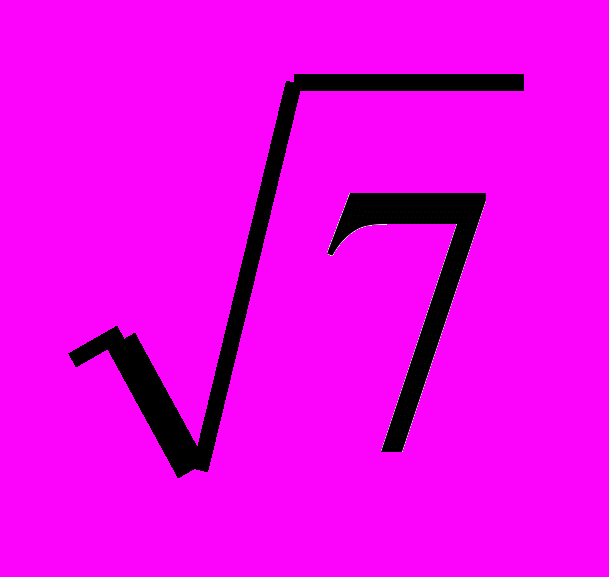2. Образует ли подмножество H = {11k, kÎZ} подгруппу группы ?

3.Построить фактор-группу аддитивной группы 2Z по подгруппе 6Z?

4. Найти левое и правое разложение симметрической группы подстановок S3 по циклической подгруппе, порождённой подстановкой f = .

5. Доказать изоморфизм групп и <5Z, +>.


Контрольная работа № 2 по теме: «Группа подстановок и ее свойства»

1. Изобразить с помощью стрелочных схем и найти произведение a×b, если a =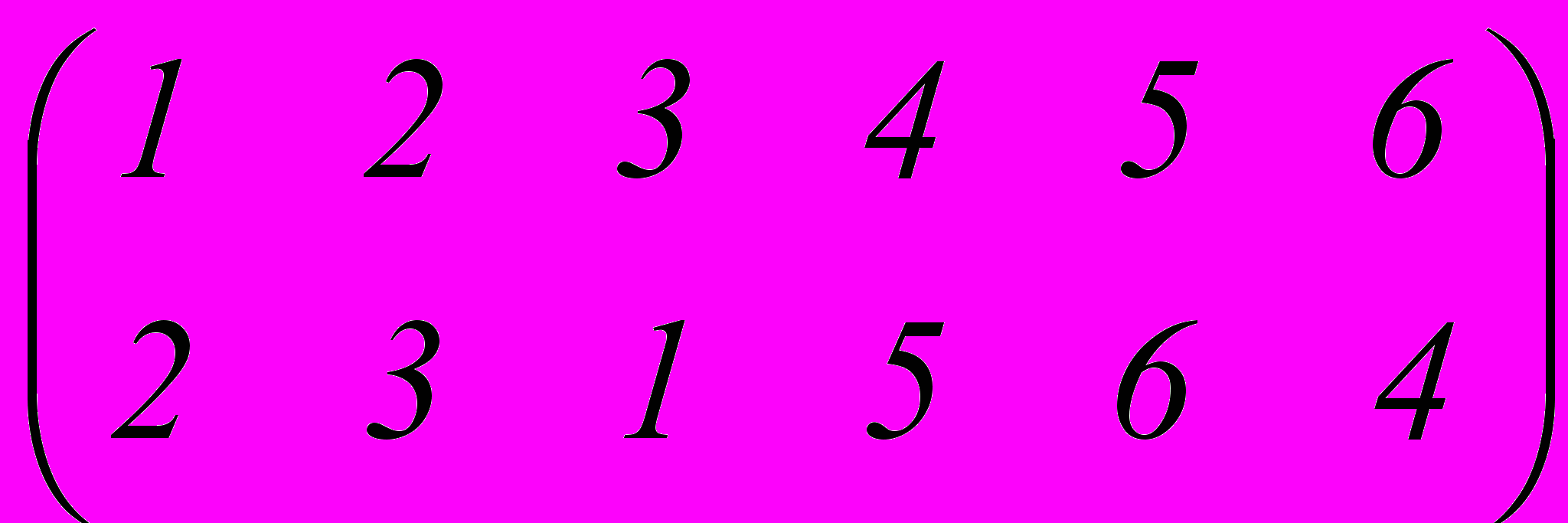, b =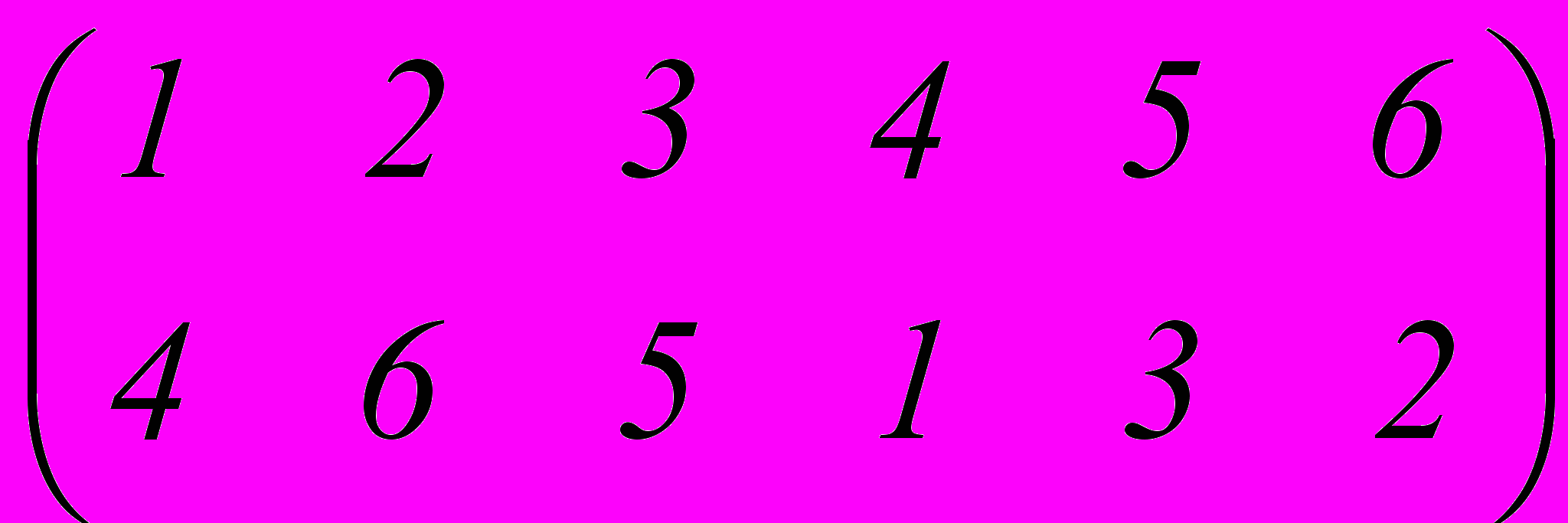

2. Решить уравнение:

x × =

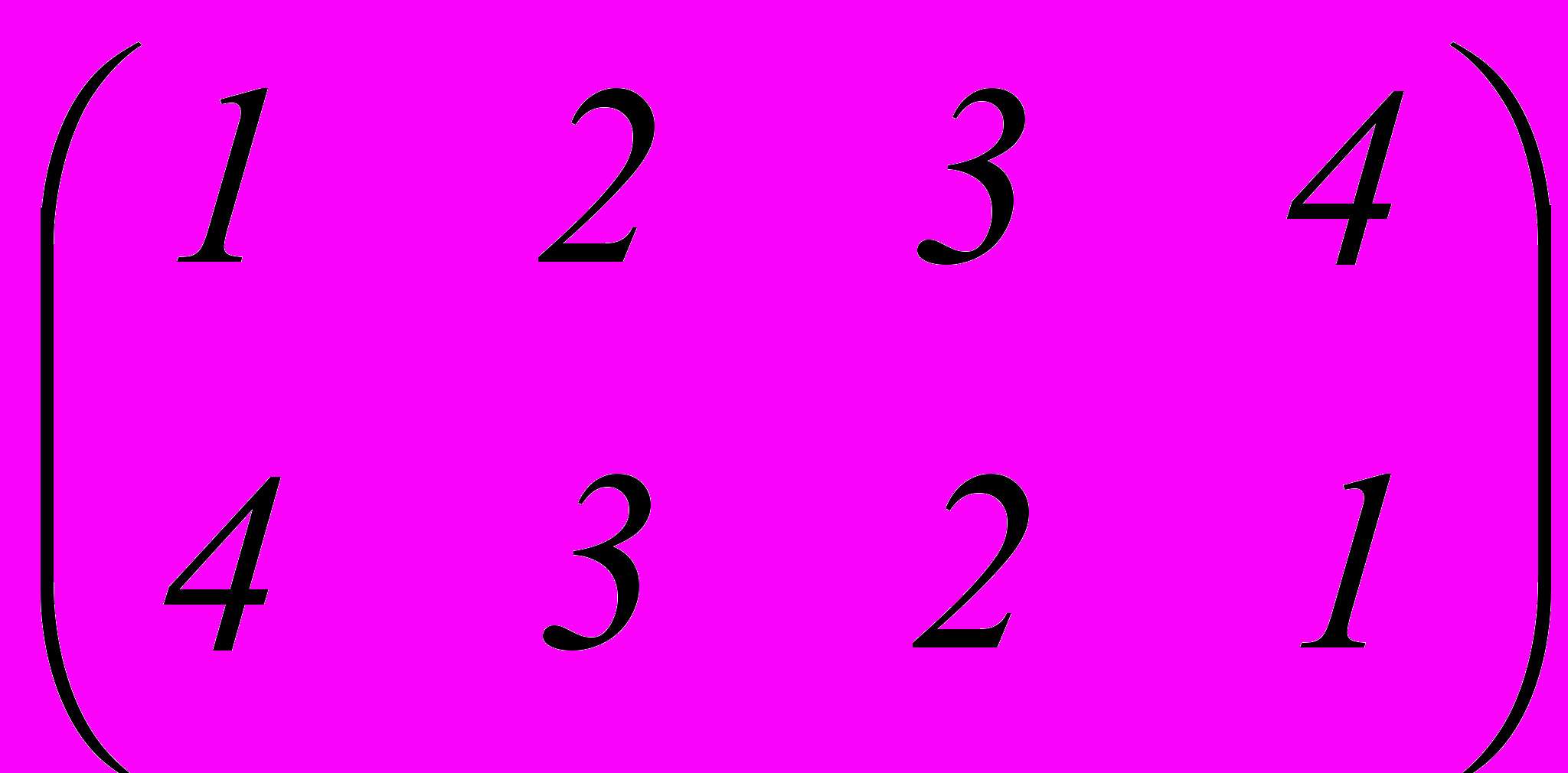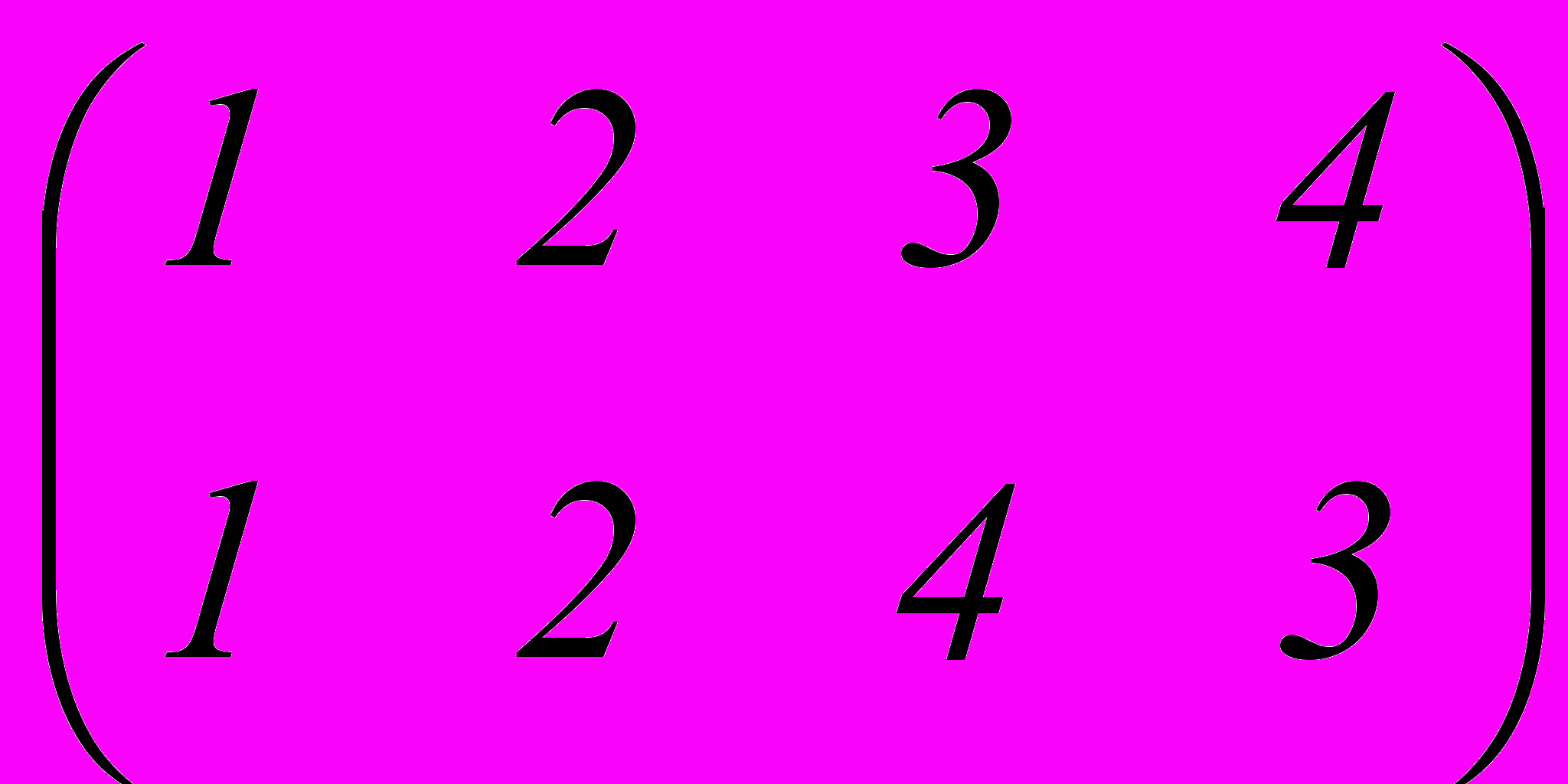
3. Разложить в произведение независимых циклов и найти порядок подстановки j. Вычислить j -25 , если j =.

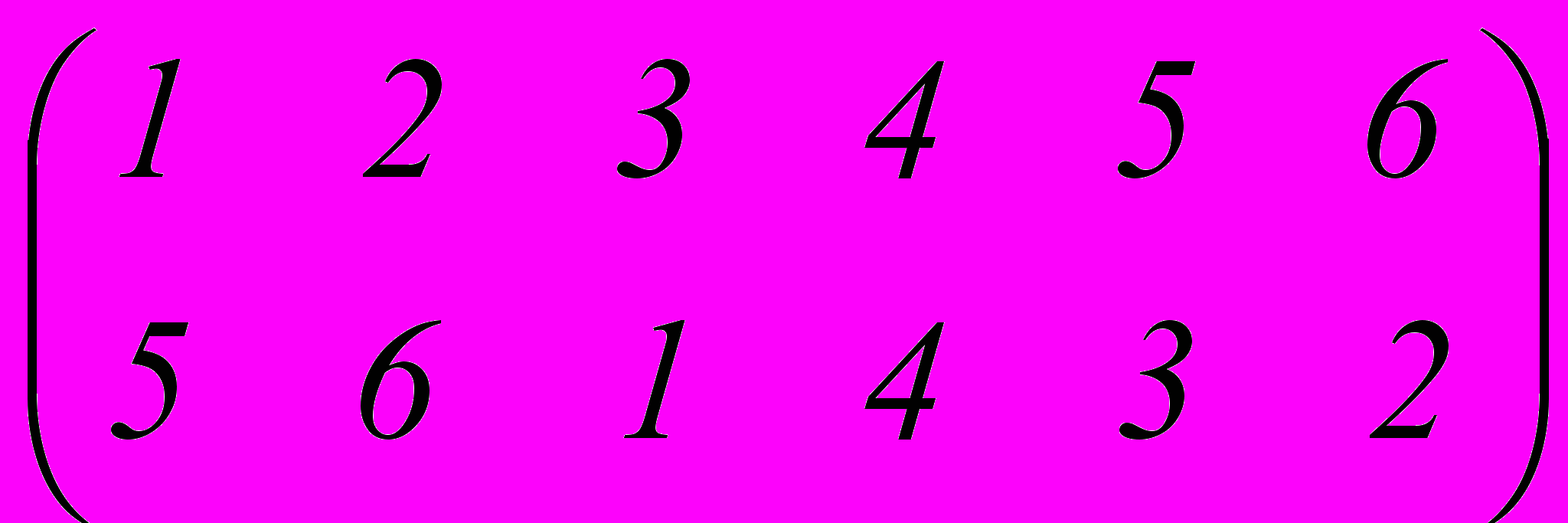4. Образует ли H={e, (2,3)} подгруппу в S3? Ответ обосновать.

5. Является ли подстановка четной?

j =.

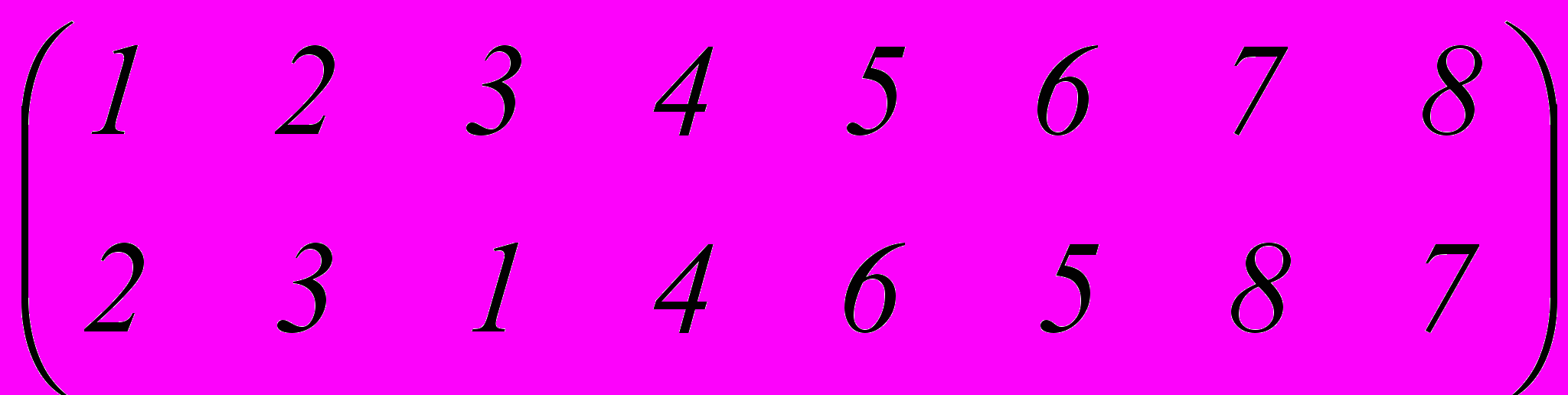6. Разложить подстановку из №3 в произведение элементов системы:

{(1, 2), (1, 3), (1, 4), (1, 5), (1, 6)}.

ПРИМЕРНАЯ ТЕМАТИКА ДОКЛАДОВ И РЕФЕРАТОВ ПО ДИСЦИПЛИНЕ

“ ИЗБРАННЫЕ ВОПРОСЫ ТЕОРИИ ГРУПП”

1. Суперпозиция функций и умножение преобразований (3,16,23,31)

2. Группа подстановок (3,16,23,31)

3. Графы преобразований. Орбиты. Циклическая форма записи подстановок (3,16,23, 31).

  1. Порядок подстановки (3, 16, 23, 31).
  2. Образующие симметрической группы (3, 16, 23, 31).
  3. Подгруппы симметрических групп (3, 16, 23, 31).
  4. Группы симметрий (3, 9, 16, 22, 31).
  5. Теорема Лагранжа (3, 16, 31).
  6. Орбиты группы подстановок. Лемма Бернсайда (10, 16).
  7. Комбинаторные задачи (10, 16).
  8. Действие подстановки на многочлен (16).
  9. Четные и нечетные подстановки. Знакопеременная группа (3, 16, 23, 31).
  10. Симметрические и четносимметрические многочлены (16).
  11. Решение алгебраических уравнений (16,13).
  12. Подстановки и математические игры (10, 16).


Основная литература

  1. Евсюкова Е.В. Введение в теорию групп: Учебно-методическое пособие для студентов физико-математических специальностей. – Тобольск: изд-во ТГСПА им. Д. И. Менделеева, 2010. – 153 с.
  2. Куликов Л. Я. Алгебра и теория чисел: Учеб. пособие для педагогических институтов. – М.: Высш. Школа, 1979.


Дополнительная литература
  1. Александров П.С. Введение в теорию групп (библиотечка «Квант»). М.: Наука,
  2. 1980 – 143с.
  3. Алексеев В.Б. Теория Абеля в задачах и решениях . М.: Наука, 1980 – 207с.
  4. Бердон М. Геометрия дискретных групп. М.: Наука, 1986.- 300с.
  5. Берже М. Геометрия. Т.1. М.: Мир, 1984 – 548с.
  6. Берже М., ери Ж. – П., Пансюн., Сен-Реймон К. Задачи по геометрии с коммента­риями и решениями. М.: Мир,1989.- 304с.
  7. Болтянский В.Г., Виленкин Н.А. Симметрия в алгебре. М., 1967.
  8. Вейль Г. Симметрия. М.: Наука, 1968. – 191с.
  9. Виленкин Н.Я. Популярная комбинаторика. М.: Наука, 1975. – 208с.
  10. Гильберт Д., Кон-Фоссен С. Наглядная геометрия. М.: Наука, 1981. – 344с.
  11. Гроссман И., Магнус В. Группы и их графы. М.:Мир, 1971. – 247с.
  12. Дальма А. Эварист Галуа – революционер и математик. М.: Наука, 1984.
  13. Дужин С.В., Чеботаревский Б.Д. От орнаментов до дифференциальных уравнений. Минск: Выш. шк., 1988. – 253с.
  14. Долбилин Н.П. Правильные системы. М.: Изд-во «Знание» №12, 1978г. (Серия «Математика, кибернетика» – 62с.)
  15. Калужнин Л.А., Сущанский В.И. Преобразования и перестановки. М.: Наука,1985. – 112с.
  16. Каргаполов М.И., Мерзляков Ю.И. Основы теории групп. М.: Наука, 1972. – 238с.
  17. Клейн Ф. Сравнительное обозрение новейших геометрических исследований /Эрлангенская программа/, 1872.- В сб.: Об основаниях геометрии. М.: Гостехиздат, 1956.- с.399-434.
  18. Клейн Ф. Элементарная математика с точки зрения высшей: в 2-х томах. Т.2. Геометрия: Пер. с нем. / Под ред. В.Г.Болтянского. – 2-е изд. М.: Наука, Гл. ред. физ.-мат. лит.,1987.- 416с.
  19. Коксетер Г.С.М. Введение в геометрию. М.:Мир, 1971.- 247с.
  20. Колмогоров А.Н. Паркеты из правильных многоугольников. // Квант.-1986.№6.С.3-7.
  21. Кукин Г.П., Кузнецова О.В. Лекции о симметрии. Омский ун-т, 1993. – 103с.
  22. Ляпин Е.С., Айзенштат А.Я., Лесохин М.М. Упражнения по теории групп. М.: Наука,1967.-264с.
  23. Моденов П.С., Пархоменко А.С. Геометрические преобразования. М.: Изд-во МГУ, 1961.- 231с.
  24. Молодший В.И. Очерки по философским вопросам математики. М.: Просвещение, 1969. – 303с.
  25. Земляков А. Орнамент. // Квант. – 1977.№3
  26. Постников М.М. Теория Галуа, М.,1963.
  27. Тимирбулатова А.М. Правильные системы. Дипломная работа. Тобольский пед. институт, 2001г.
  28. Федоров Е.С. Правильное деление плоскости и пространства. Л.: Наука, 1979. – 272с.
  29. Федоров Е.С. Симметрия и структура кристаллов: основные работы / Ред. А.В. Шубникова, И.И. Шафрановского. Симметрия правильных систем точек. М.: АН СССР, 1949.-С.111-255.
  30. Фрид Э. Элементарное введение в абстрактную алгебру. М.: Мир, 1979. – 260с.
  31. Яглом И.М. Феликс Клейн и Софус Ли. М.: Знание, 1977.-64с.
  32. Яглом И.М., Болтянский В.Г. Выпуклые фигуры. М.-Л. Гостехиздат, 1957. – 343с.


К.п.н., доцент ____________________ Евсюкова Е.В.