Формы представления моделей

Вид материала

Документы

Содержание Формы представления моделей На первом этапе На втором этапе На третьем этапе На четвертом этапе На шестом этапе Алгоритм и его свойства Исполнитель алгоритма

Подобный материал:

• 1. Классификация моделей представления знаний, 1008.73kb.
• Лекции по дисциплине «Математическое моделирование» для студентов и магистрантов специальности, 21.92kb.
• 1 Формы представления модели, 61.63kb.
• Тема: «Моделирование, как метод познания», 55.31kb.
• Доклад Целью данной работы является разработка моделей и средств формализованного представления, 57.62kb.
• Программа вступительного испытания (собеседование/устный экзамен) по дисциплинам «Информационная, 30.7kb.
• Разработка новых моделей школьной формы в официально-деловом стиле, 237.83kb.
• Контрольная работа по курсу «Высшая математика (раздел «Математическое программирование»)», 24.35kb.
• Техническое задание на выполнение курсовой работы на тему: Исследование моделей представления, 32.74kb.
• Программа обсуждена на заседании кафедры Математики фнти, 27.07kb.

Содержание


Этапы решения задач на ЭВМ. Моделирование и формализация …2

Алгоритм и его свойства ……………………………………………...5

Алгоритмическая структура ветвление ……………………………..10

Циклические алгоритмы ……………………………………………..13


Этапы решения задач на ЭВМ. Моделирование и формализация

С различными моделями и модельными представлениями мы встречаемся каждодневно и ежечасно. Моделями являются фотография, карта дорог, географическая карта, рисунок, картина, различные описания и т.д.

Модели незаменимы в физике, химии, биологии, математике, информатике. Выбор модельных представлений часто определяет успех научных исследований, т.к. от него зависит точность и достоверность получаемых выводов, прогнозов и рекомендаций.

Моделирование – это метод познания, состоящий в создании и исследовании моделей.

Модели по своей сути – чисто информационное понятие.

Модель – отражение наиболее существенных признаков, свойств, отношений, явлений, объектов или процессов предметного мира (фотографии и рисунки – это представление внешнего вида предметов, а чертежи раскрывают их структуру (внутреннюю организацию)).

Для одних и тех же объектов, процессов и явлений можно построить различные модели, а разные объекты могут описываться одной моделью. Многообразие модельных представлений, связываемых с одними и теми же объектами, отражает различие точек зрения, интересов, потребностей людей в изучении этих объектов. В математике и информатике модели служат основой для постановки задачи.

Формы представления моделей

Все модели можно разбить на два больших класса: модели предметные (материальные) и модели информационные. Пред­метные модели воспроизводят геометрические, физические и другие свойства объектов в материальной форме (глобус, анатомические муляжи, модели кристаллических решеток, макеты зданий и сооружений и др.).

Информационные модели представляют объекты и про­цессы в образной, знаковой или вербальной форме.

Образные модели (рисунки, фотографии и др.) представ­ляют собой зрительные образы объектов, зафиксированные на каком-либо носителе информации (бумаге, фото- и кино­пленке и др.). Широко используются образные информаци­онные модели в образовании (учебные плакаты по различным предметам) и науках, где требуется классифи­кация объектов по их внешним признакам (в ботанике, био­логии, палеонтологии и др.).

Знаковые информационные модели строятся с использо­ванием различных языков (знаковых систем). Знаковая ин­формационная модель может быть представлена в форме текста (например, программы на языке программирования), формулы (например, второго закона Ньютона Р = т•а), таб­лицы (например, периодической таблицы элементов Д.И. Менделеева) и так далее.

Вербальный - в мысленной или разговорной форме.

Работа по решению задач с использованием компьютера проходит через следующие этапы:


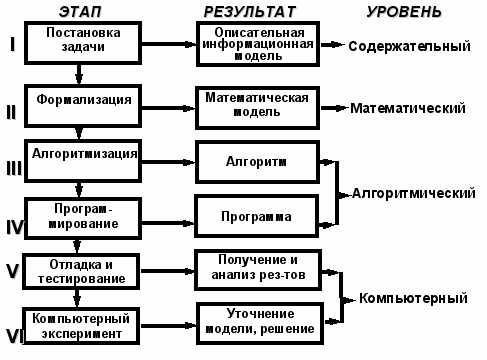
На первом этапе обычно строится описательная информационная модель объекта или процесса. При этом должно быть четко опреде­лено, что дано (какие исходные данные извест­ны, какие данные допустимы) и что требуется найти в решаемой задаче. Также должны быть четко выделены наиболее существенные свой­ства рассматриваемого объекта или процесса, указаны связи между исходными данными и ре­зультатами.

На втором этапе описательная информаци­онная модель формализуется, т. е. записывается с помощью некоторого формального языка. Для этого требуется:

• понять, к какому классу принадлежит рас­сматриваемая задача;

• записать известные связи между исходны­ми данными и результатами с помощью мате­матических соотношений;

• выбрать наиболее подходящий способ для решения задачи.

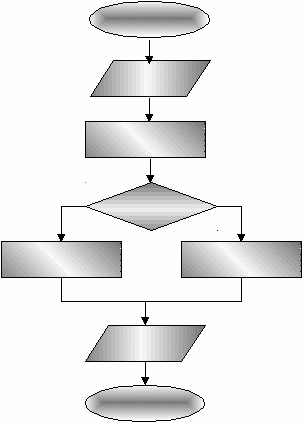
На третьем этапе осуществляется постро­ение алгоритма — четкой инструкции, задающей необходимую последовательность действий для решения задачи. Алгоритм чаще всего представ­ляется в форме блок-схемы, в силу ее нагляднос­ти и универсальности.

На четвертом этапе алгоритм записываем на понятном для компьютера языке, например, на одном из языков программирования.

На пятом этапе осу­ществляется отладка и тестирование програм­мы. Отладка программы — это процесс провер­ки работоспособности программы и исправле­ния обнаруженных при этом ошибок. Ошибки могут быть связаны, например, с нарушением правил записи программы на конкретном языке программирования. Их программисту помогает обнаружить используемая система программи­рования, выдавая на экран сообщения о выяв­ленных синтаксических и семантических ошиб­ках. Проверка правильности разработанного алгоритма осуществляется с помощью тестов. Тест — это конкретный вариант значений ис­ходных данных, для которого известен ожидае­мый результат.

На шестом этапе осуществляется компьютерный эксперимент, состоящий в проведении расчетов с заданными исходными данными, со­поставлении полученных результатов с экспе­риментальными фактами, теоретическими по­ложениями и т.д. При этом может возникнуть необходимость уточнить разработанную мате­матическую модель, полнее учесть особенности изучаемого объекта или процесса. По уточнен­ной математической модели снова составляется алгоритм, проводится компьютерный экспери­мент, анализируются результаты. Так продол­жается до тех пор, пока полученные результаты не будут достаточно точно соответствовать изу­чаемому объекту.

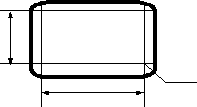
З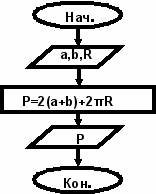адача №1. Определить периметр крышки стола. Нас интересуют лишь размеры крышки стола, поэтому заменим реальный объект «стол» плоской геометрической фигурой, размеры и конфигурация которой соответствуют поверхности крышки.

Радиусы закруглений равны, следовательно,

Исходные данные: r, a, b

Результат: Р

Вычислить значение Р: Р=2(a+b)+2πr


АЛГОРИТМ И ЕГО СВОЙСТВА


Каждый из нас ежедневно использует различные алгоритмы: инструкции, рецепты, правила и т.п. Обычно мы это делаем, не задумываясь. Примеры.

1. Изучим расписание занятий на следующий день: Физика.

Математика.

Русский язык.

Физическое воспитание.

Начинаем подготовку к этим занятиям в соответствии с расписанием.

2. Открывая ключом дверь своей квартиры, вы должны выполнить следующие действия: достать ключ, вставить ключ в замочную скважину, повернуть ключ 2 раза против часовой стрелки, вынуть ключ.

3. Получив приглашение в гости, вы просите подробное и точное описание, как добраться до указанного места: выйти из дома, повернуть направо, пройти 2 квартала до автобусной остановки, сесть в автобус 30, идущий к центру города, проехать 3 остановки, выйти из автобуса.

Ha первый взгляд эти 3 алгоритма не имеют между собой ничего общего. Однако при внимательном изучении можно заметить одно существенное сходство - строгий порядок выполнения действий. Правда, алгоритм 1 как частный случай выполняется при любом порядке действий, предложенных в нем. Но алгоритм 2 при перестановке, например, 2 и 3 действий может быть выполнен, но не приведет к желаемому результату - дверь не будет открыта. Если же в алгоритме 3 поменять местами 4 и 5 действия, он станет невыполняемым. Таким образом, для алгоритма важен не только набор действий, но и то, как они организованы, т.е. в каком порядке выполняются. Это общее свойство всех алгоритмов.

Теперь мы можем сказать, что А Л Г О Р И Т М - это организованная последовательность действий. Это формулировка не может считаться определением алгоритма, т.к. не объяснены понятия "организованная" и "действия". Абсолютно строгого определения алгоритма не существует. Это - одно из фундаментальных понятий информатики. Такое же, как понятие точки, прямой и плоскости в геометрии, пространстве и времени в физике, вещества в химии и т.д.

Понятие алгоритма возникло и используется давно, значительно раньше появления компьютеров. Само слово «алгоритм» происходит от латинской формы написания имени выдающегося математика средневекового Востока Мухаммеда Аль-Хорезми, который сформулировал правила выполнения арифметический действий. Но широким распространением это понятие обязано основополагающей идее - идее автоматизации поведения исполнителя - автомата, реализуемой на основе алгоритма.

Исполнитель алгоритма - некоторое устройство управления, соединенное с набором инструментов.

Устройство управления понимает алгоритмы и организует их выполнение, командуя соответствующими инструментами.

Инструменты производят действия, выполняя команды управляющего устройства.

Исполнителем алгоритма мажет быть:

- человек;

- животное;

- техническое устройство.

Исполнителя характеризуют:

- среда - это обстановка, в которой функционирует исполнитель;

- элементарные действия;

- система команд;

- отказы - возникают, если команда вызывается при недопустимом для нее состоянии среды.

Предписание о выполнении отдельного законченного действия исполнителя называется командой алгоритма. Совокупность всех команд, которые могут быть выполнены некоторым исполнителем, образует СКИ – систему команд данного исполнителя. Задача обучения алгоритмизации заключается в том, чтобы научить составлять запись алгоритмов, причем делать это так, чтобы воображаемый исполнитель мог однозначно и точно следовать предписаниям алгоритма и эффективно получать определенный результат. Это накладывает на записи алгоритмов целый ряд обязательных требований, которые мы сформулируем в виде перечня свойств, которым должны удовлетворять все алгоритмы.

1. Дискретность (прерывность).

Описываемый процесс должен быть разбит на последовательность отдельных шагов. Возникающая при этом запись представляет собой упорядоченную совокупность четко разделенных друг от друга предписаний (директив, команд), образующих прерывную (дискретную) структуру алгоритма: только выполнив требования одного предписания, можно приступить к выполнению следующего.

2. Понятность.

Используемые на практике записи алгоритмов составляются с ориентацией на определенного исполнителя. Составляя алгоритм, нужно знать, какие предписания этот исполнитель может понять и исполнить, а какие нет. У каждого исполнителя имеется свой перечень предписаний, которые для него понятны и которые он может исполнить. Такой перечень называют системой команд исполнителя (СКИ). Составляя запись алгоритма для определенного исполнителя, можно использовать лишь те команды, которые входят в его СКИ.

3.Определенность (детерминированность).

Будучи понятным, алгоритм не должен содержать предписаний, смысл которых воспринимается неоднозначно, т.е. алгоритм не должен оставлять места для произвола исполнителя. Предписание типа "Взять 2-3 ложки сахарного песка" или "умножить х на одно из двух данных чисел a или b" недопустимы в записи алгоритма. Кроме того, в алгоритмах недопустимы ситуации, когда после выполнения очередного предписания исполнителю не ясно, какое предписание алгоритма должно выполняться на следующем шаге.

4. Массовость

Наиболее предпочтительными являются алгоритмы, обеспечивающие решение широкого класса задач данного типа. В простейшем случае алгоритм должен обеспечивать возможность использования различных допустимых значений исходных данных, например: решение квадратного уравнения ах ²+ вх +с = 0 в области действительных чисел может быть найдено по формулам, которые применимы не для одного, а для многих квадратных уравнений с коэффициентами а,b,с, удовлетворяющими условию: D = b² -4ас > 0

5. Результативность

Это обязательное требование к алгоритмам, смысл которого состоит в том, что при точном исполнении всех предписаний алгоритма процесс должен прекратиться за конечное число шагов и при этом должен быть получен какой-либо определенный ответ на вопрос задачи.

Теперь с учетом рассмотренных свойств алгоритма (в частности, свойства 2) мы можем уточнить понятие алгоритма.

А Л Г О Р И Т М - это строго определенная последовательность действий, описывающая процесс преобразования объекта из начального состояния в конечное, записанная с помощью понятных исполнителю команд.

Разработка алгоритма – трудоемкая задача, требующая от человека глубоких знаний и больших временных затрат. Решение задачи по готовому алгоритму требует от исполнителя только строгого следования заданным предписаниям. Исполнитель не обязан вникать в смысл того, что он делает, и рассуждать, почему он поступает так, а не иначе, т.е. он действует формально – по командам.


Типы алгоритмических структур

1. Линейный алгоритм

2. Алгоритм с ветвлением

3. Циклический алгоритм

Алгоритм, в котором действия совершаются строго одно вслед за другим, называется ЛИНЕЙНЫМ.

Такими, например, будут алгоритмы вычислений по простейшим формулам: площадь круга, длина окружности, квадрат гипотенузы и т.д.

Алгоритмы бывают правильные и неправильные (действия выполнены, но необходимый результат не получен).

Для описания алгоритмов используют определенную форму записи - алгоритмический язык. Запись алгоритма должна оформляться по следующим правилам.

На первой строке записывается слово алгоритм или его трехбуквенное сокращение  алг. Далее за этим словом записывается название алгоритма.

На второй строке записывается слово начало или его сокращение  нач.

Далее в столбик записываются действия, составляющие алгоритм. Последней строкой описания алгоритма должно быть слово конец или  кон. в той же позиции, что и слово  начало. Общая форма записи: алг. <название алгоритма>

нач. <составные команды>

действия

кон. <конец>

В алгоритмической форме можно записывать не только алгоритмы для вычислительных машин, но и различные инструкции, предписания и рекомендации для людей.

Например:

Кипячение чайника.

 алг. < Кипячение чайника.>

нач

налить в чайник воды

зажечь газовую конфорку

поставить чайник на огонь

когда чайник закипит, выключить газ

снять чайник с плиты

кон.

Очень часто алгоритмы описываются с помощью языка блок-схем.

Блок-схема — графическое представление, элементы которого соответствуют выполняемым предписаниям и представляют собой геометрические фигуры, определенные ГОСТ

Символ	Обозначение
	Начало, конец алгоритма
	Ввод и вывод данных
	Действие
	Проверка условия
	Начало цикла

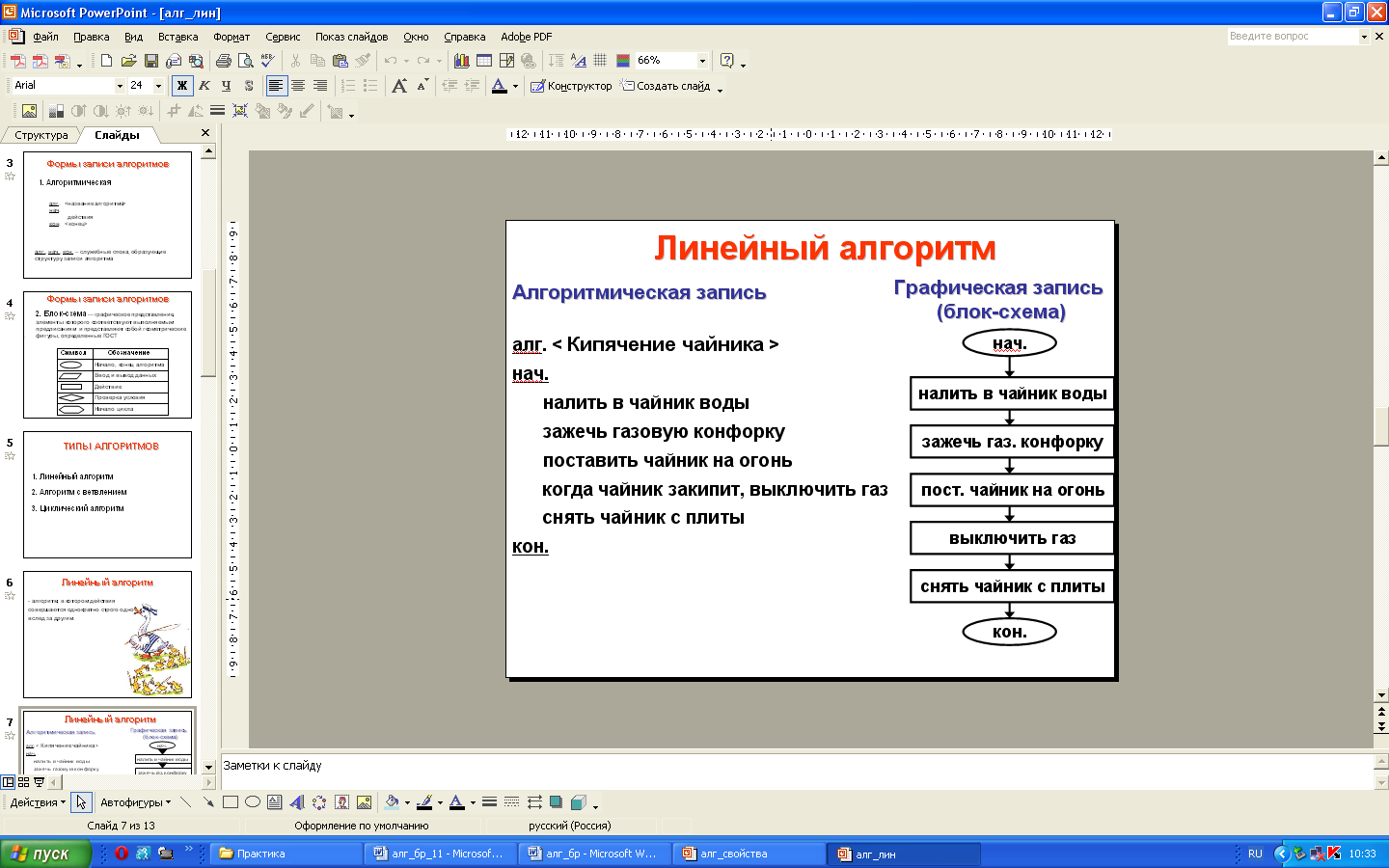
Тогда алгоритм для кипячения чайника с помощью блок - схемы можно описать следующим образом:


ЗАДАНИЕ

1. Записать в алгоритмической форме и составить блок-схему к следующему алгоритму:

Вычисление гипотенузы прямоугольного треугольника по двум катетам с помощью калькулятора.

2. Какие действия вы бы добавили, чтобы был выполнен следующий алгоритм переправы через Волгу в р-не г.Саратова?

Подойти к реке в районе г.Саратова,

войти в реку,

идти, пока не выйдешь на другой берег.