Решение логарифмических уравнений Цель: Обобщить знания по теме, сформировать умения решать логарифмические уравнения

Вид материала

Решение

Содержание Постановка цели урока. Устная работа. Историческая справка. Работа в группах Домашнее задание Задания для групп.

Подобный материал:

• Задачи урока : Проконтролировать знания учащихся по методам решения сложных логарифмических, 83.18kb.
• Урок по теме: "Показательные функции, уравнения, неравенства", 69.08kb.
• Урок математики в 6 классе по теме «Решение задач на составление уравнений», 98.1kb.
• Урок в11 классе по теме «Методы решения логарифмических уравнений. Подготовка к егэ», 66.55kb.
• «квадратные уравнения», 46.79kb.
• Решение квадратных уравнений Цели урока, 92.37kb.
• Урока алгебры и информатики «система счисления. Решение задач с помощью квадратных, 98.53kb.
• Решение нелинейных уравнений, 260.77kb.
• Урока: Урок обобщения и систематизации знаний по теме «Тригонометрические уравнения», 105.27kb.
• Решение задач повышенной сложности по теме: «Уравнения и системы уравнений», 141.17kb.

Тема: Решение логарифмических уравнений

Цель: Обобщить знания по теме, сформировать умения решать логарифмические уравнения.

Задачи:

Учебные (дидактические):

- углубить полученные теоретические знания решения логарифмических уравнений;

- систематизировать, обобщить знания, умения и навыки учащихся связанные с применением методов решения логарифмических уравнений.

Развивающие:

-развивать умение применять знания на практике;

- формировать умение выделять существенное, главное, необходимое для применения на практике;

- развивать стремление к расширению полученных знаний, умений и навыков

Воспитывающие:

- воспитывать у учащихся разнообразные интересы и способности;

- формировать навыки и потребности умственного труда,

- формировать чувство ответственности и инициативности.

Постановка цели урока.

Начало XX века. Франция. Париж. Проходя по площади Экзюпери, господин Команьон указал на дом Денизо: «Что-то больше не слышно о провидице, общавшейся со святыми. Меня водил туда Лакарель, правитель канцелярии префекта. Она сидела в кресле, закрыв глаза, а человек десять почитателей задавали вопросы… На все вопросы она отвечала в поэтическом стиле и без особого затруднения. Когда черед дошел до меня, я задал самый простой вопрос: «Каков логарифм 9?». Она мне ничего не ответила. Как же так? Провидица не знает логарифма 9? Да виданное ли это дело! Все были смущены. Я ушел, провожаемый общим неодобрением».

«Ох, опять логарифмы», - подумаете вы. А мне хочется сказать: «Ах, эти логарифмы». И сегодня на уроке мы продолжим отрабатывать навыки решения логарифмических уравнений.


Устная работа. Герберт Спенсер, английский философ, говорил: «Дороги не те знания, которые откладываются в мозгу, как жир, дороги те, которые превращаются в умственные мышцы». Вот мы сейчас и потренируем свои умственные мышцы. Я хочу вам предложить сыграть в морской бой. Я называю букву строки и номер столбца, а вы называете ответ и ищите соответствующую букву в таблице.


Ответ: Джон Непер.

	1	2	3	4	5	6	7
A	log416	Log327	log5125	log232	log39	log28	log381
B	log25125	log4 8	log279	log816	log8127	log324	log168
C	log82	log49 7	log162	log273	log1255	log644	log322
D	log66	log55	lg10	log77	log99	log42	log24
E	lg0,01	lg0,1	lg0,001	lg1000	lg	7log73	2log25

-3	5	3	1/2	1/5	1	3/4
О	Ж	Д	Н	Р	П	Е

Историческая справка. Джону Неперу принадлежит сам термин «логарифм», который он перевел как «искусственное число». Джон Непер – шотландец. В 16 лет отправился на континент, где в течение пяти лет в различных университетах Европы изучал математику и другие науки. Затем он серьезно занимался астрономией и математикой. К идее логарифмических вычислений Непер пришел еще в 80-х годах XVI века, однако опубликовал свои таблицы только в 1614 году, после 25-летних вычислений. Они вышли под названием «Описание чудесных логарифмических таблиц».


2) Альберт Эйнштейн говорил так: «Мне приходится делить время между политикой и уравнениями. Однако политика существует только для данного момента, а уравнения будут существовать вечно». Вот и сейчас в центре нашего внимания будут уравнения.


- Выберите среди предложенных выражений логарифмические уравнения.
















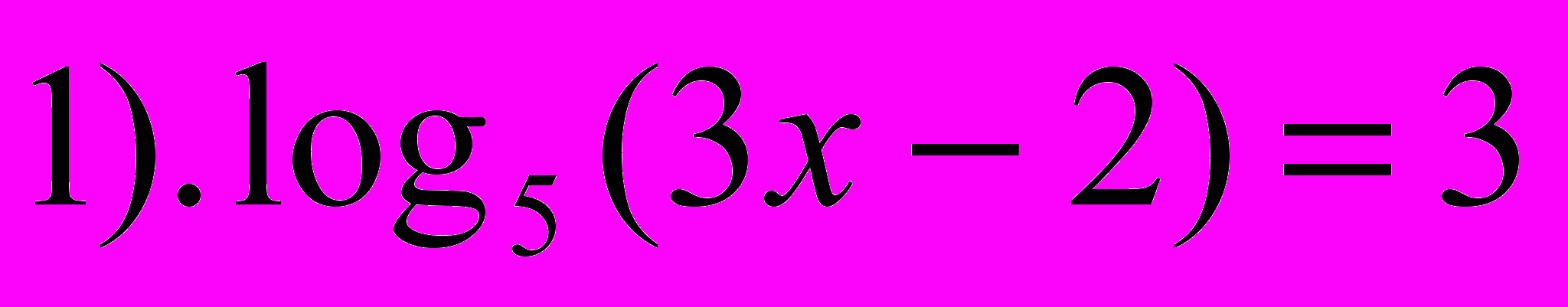
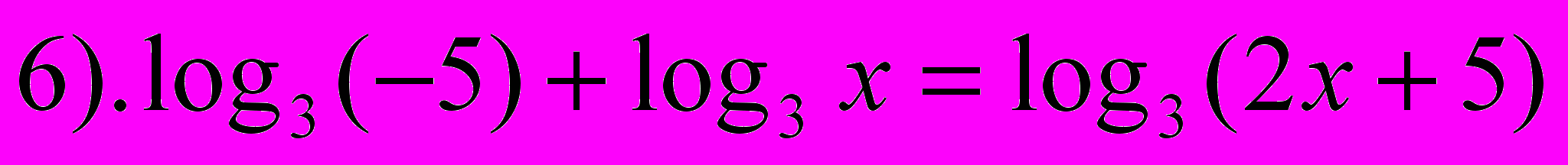
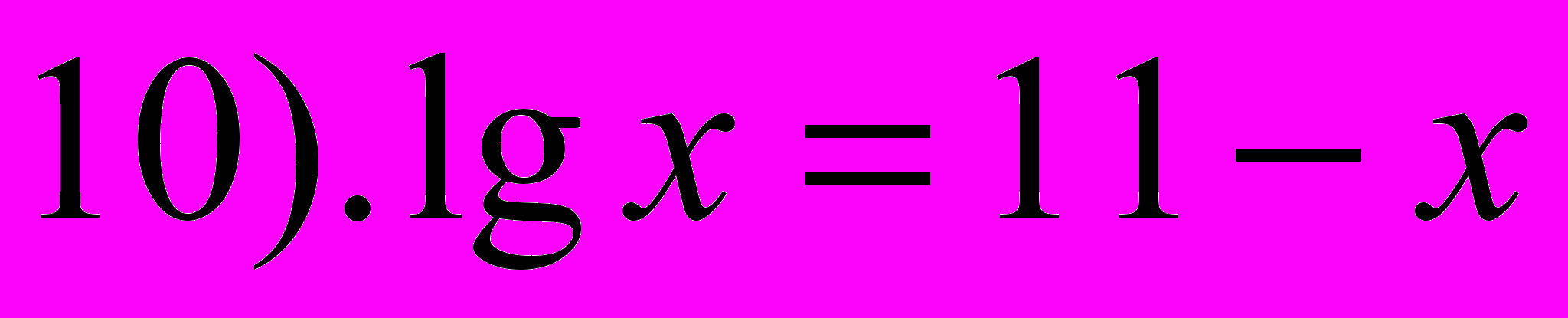
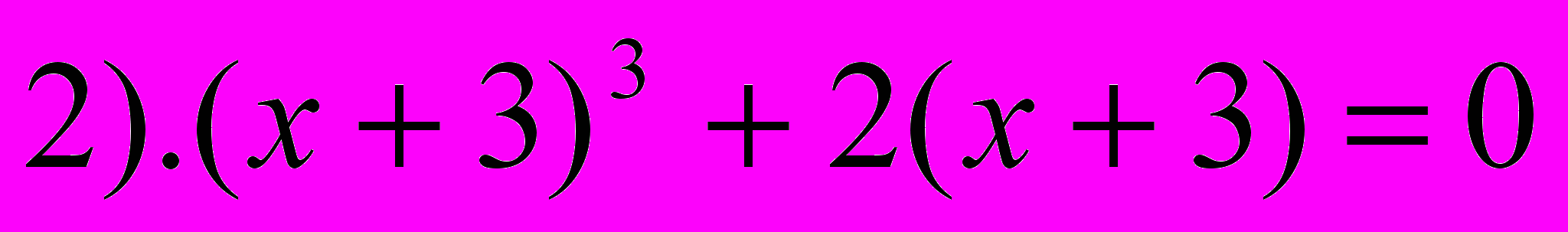
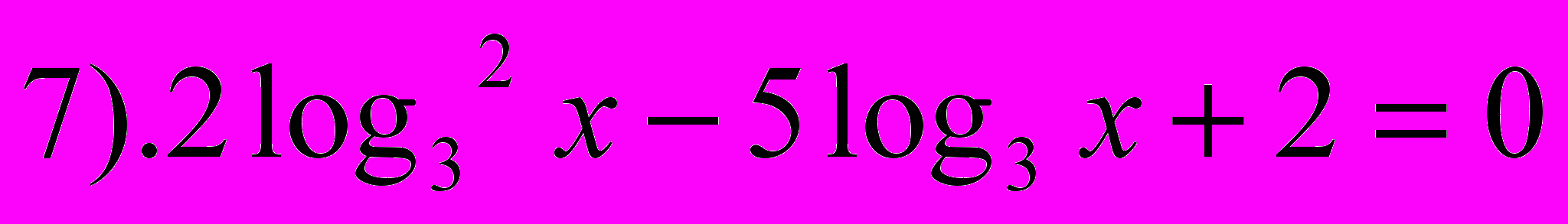
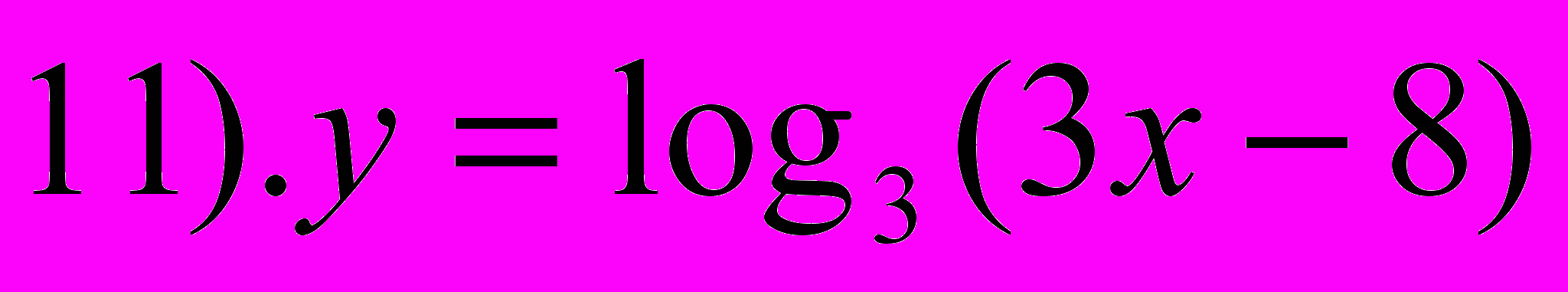
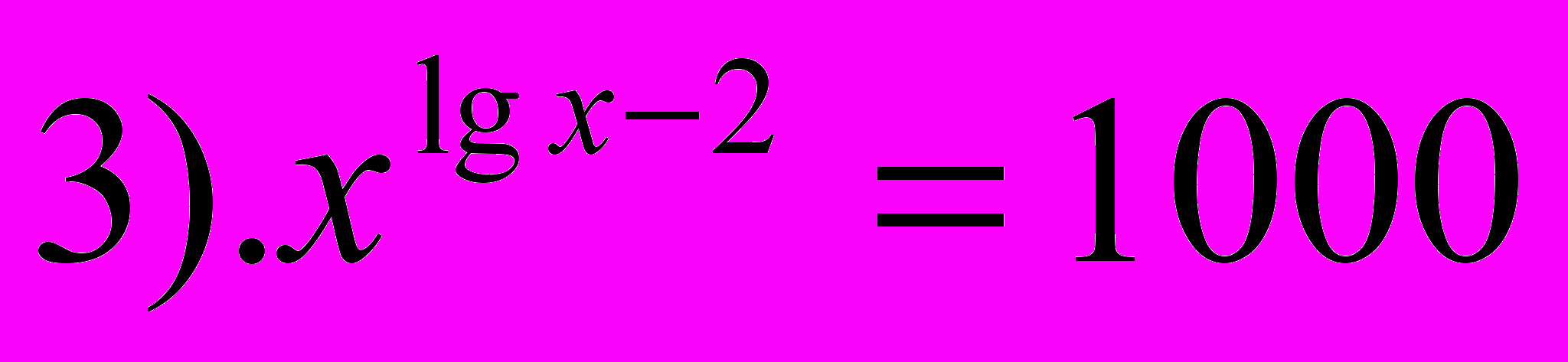
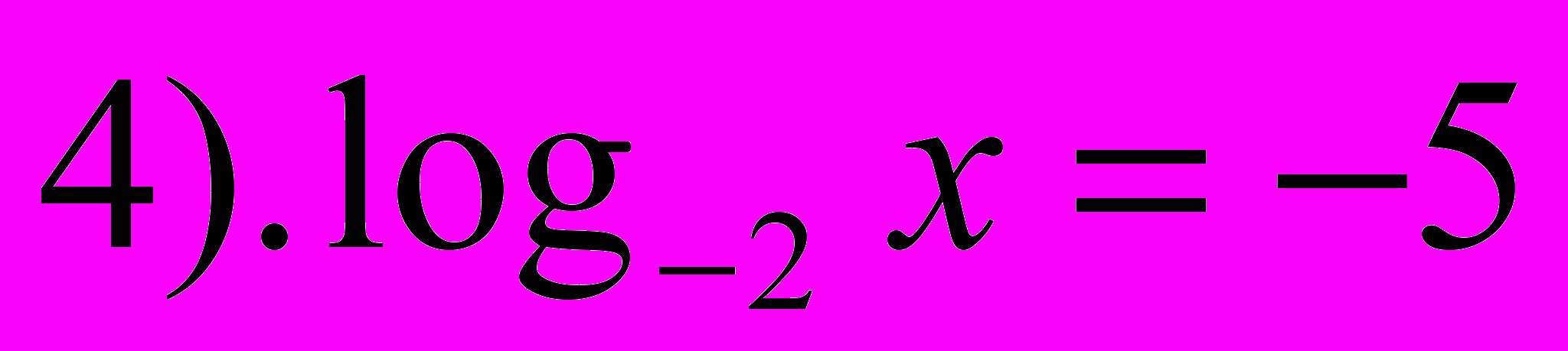
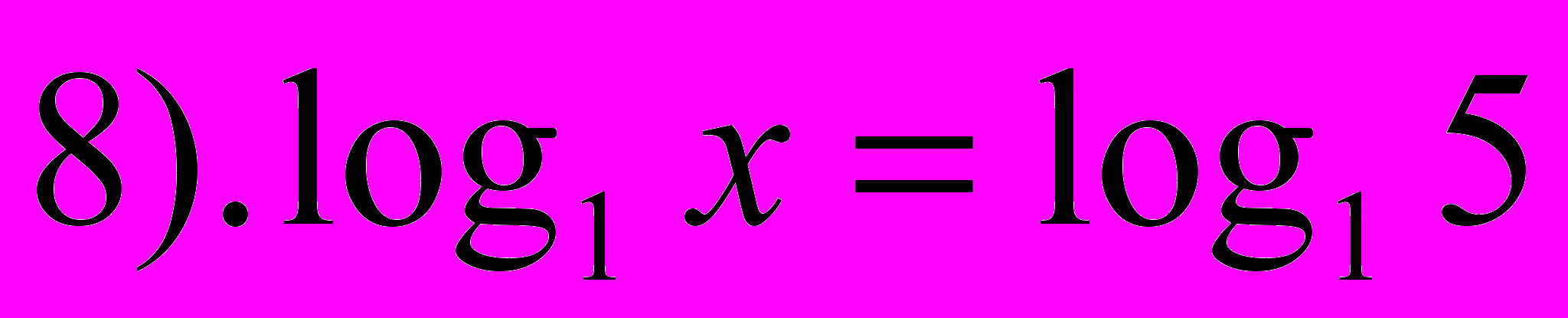
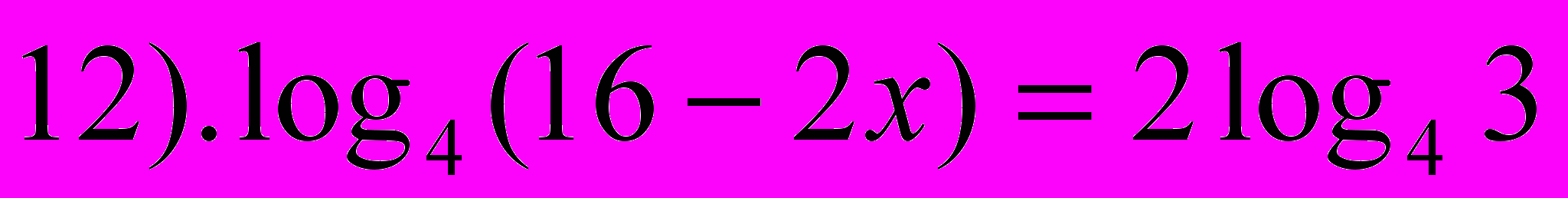
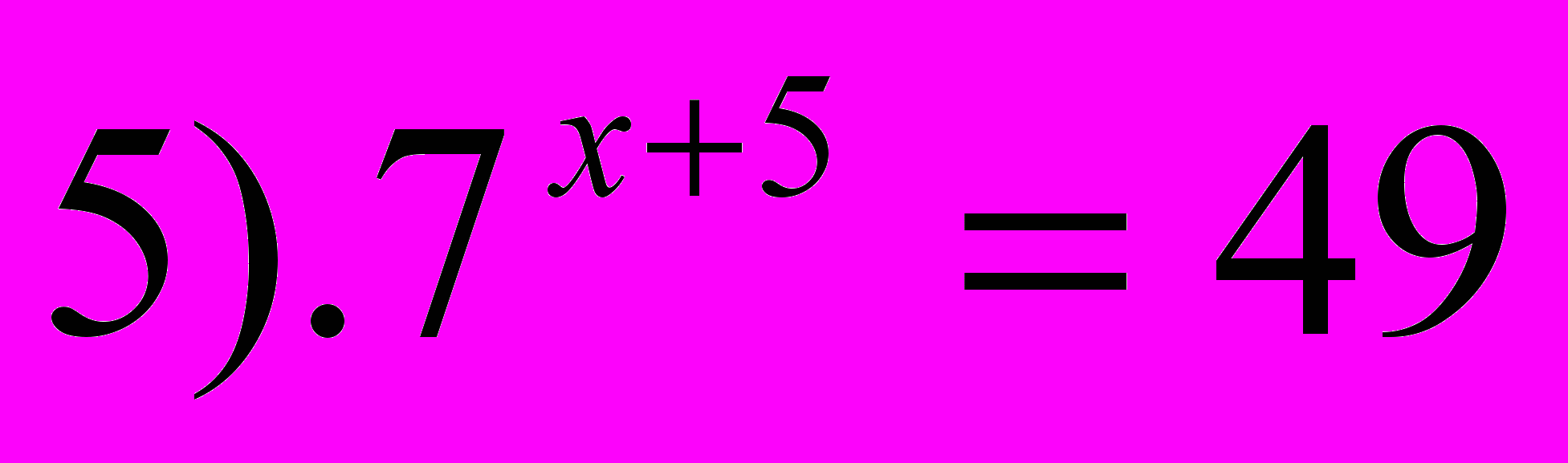
- Какие уравнения называются логарифмическими? (В которых переменная находится под знаком логарифма)

- Всегда ли логарифмическое уравнение решаемо, т.е. имеет смысл?

- Назовите номера логарифмических уравнений, которые не имеют смысла.

- Назовите методы решения, которые целесообразно использовать для этих уравнений:

1) Функционально – графический

2) Метод решения по определению логарифма

3) Метод потенцирования

4) Метод введения новой переменной

5) Метод логарифмирования

Задание: (Работа в парах)

Сколько корней имеет уравнения?

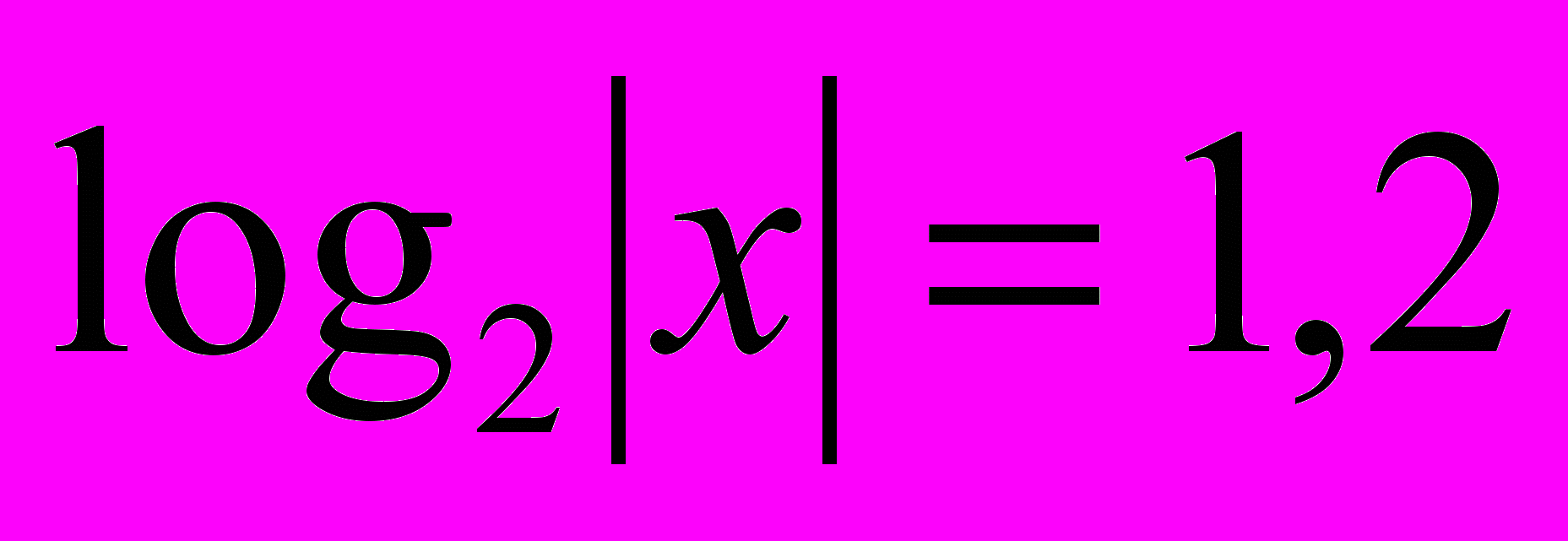Ответ: 2 решения 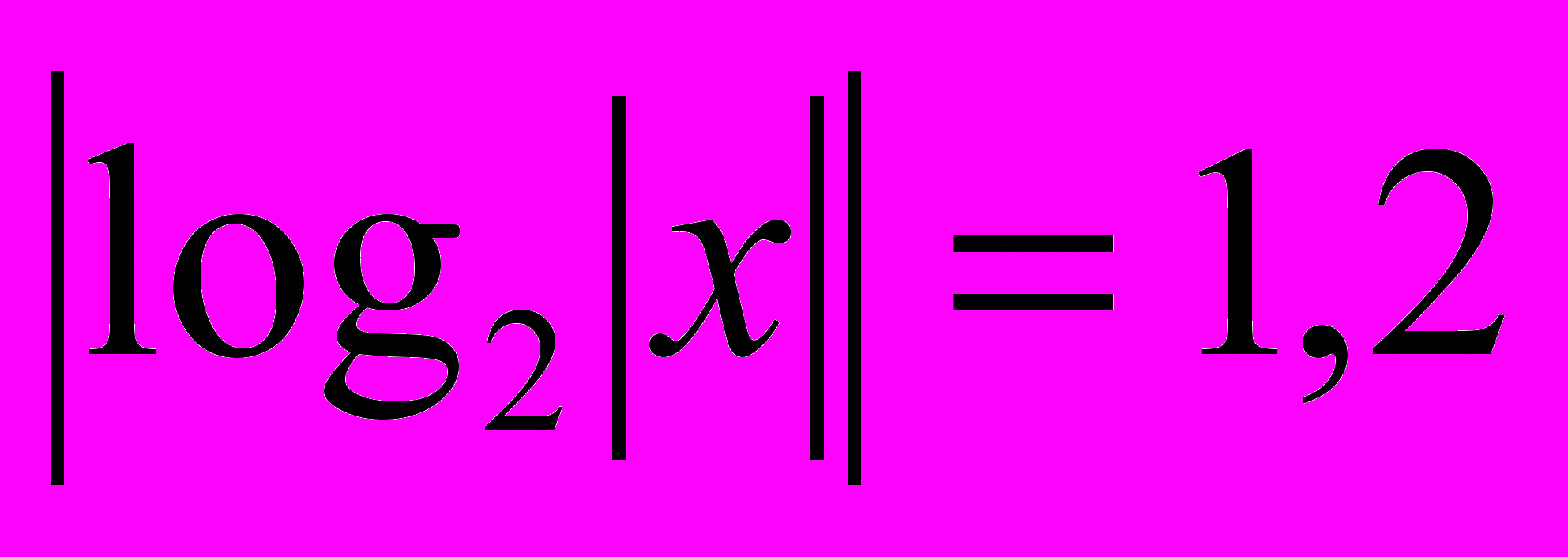Ответ 4 решения


Работа в группах: Перед вами 6 уравнений определите метод решения каждого уравнения и решите любые 3 уравнения.










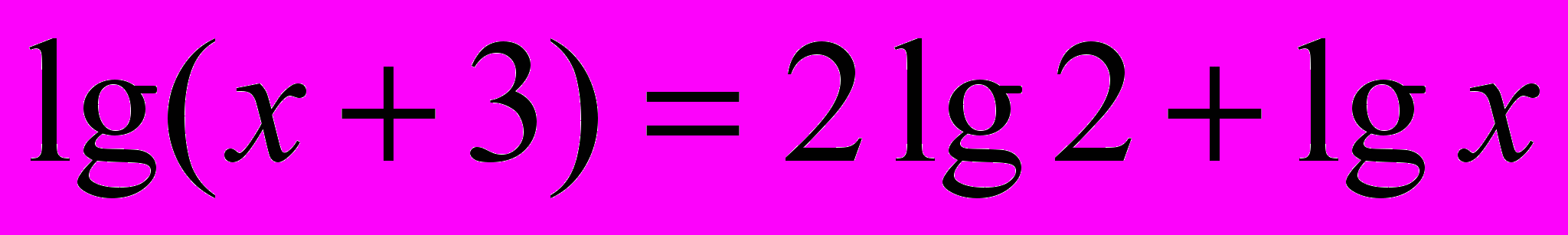
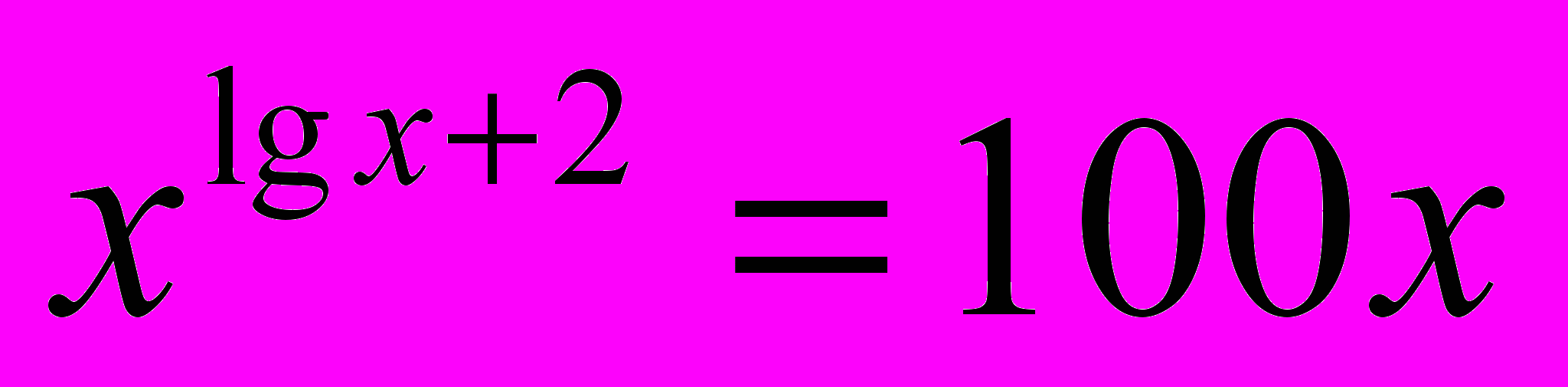
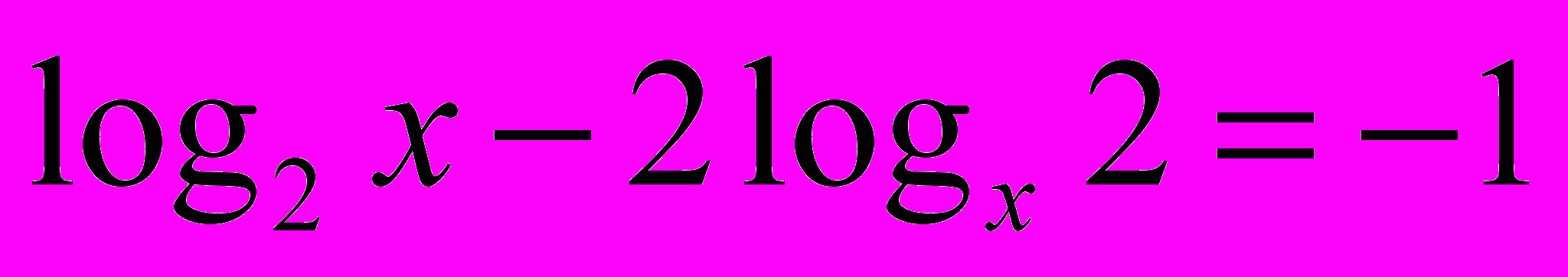
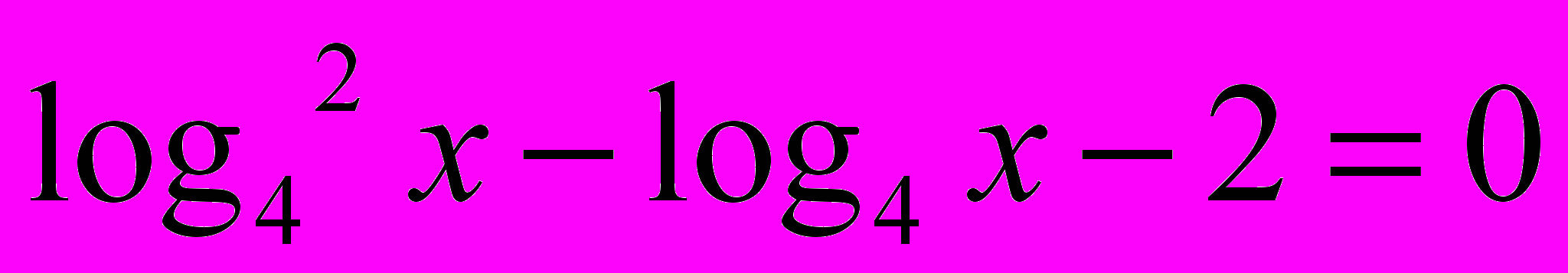
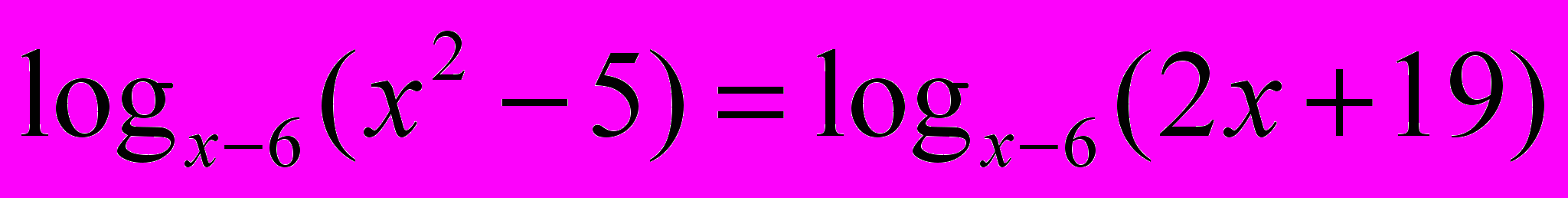
Ответы:

1. х = 1

2. х = 0,25 х = 2

3. х = 0,25 х = 16

4. х = 0,01 х = 10

5. корней нет

6. х = 1/9 х = 9


Вывод: по количеству выбранных уравнений сделайте вывод: какие методы решения логарифмических уравнений не вызывают затруднений, а над чем предстоит работать на следующих уроках. Оцените, пожалуйста, работу группы и каждого члена группы в зависимости от его активности, уровня выполненного задания.








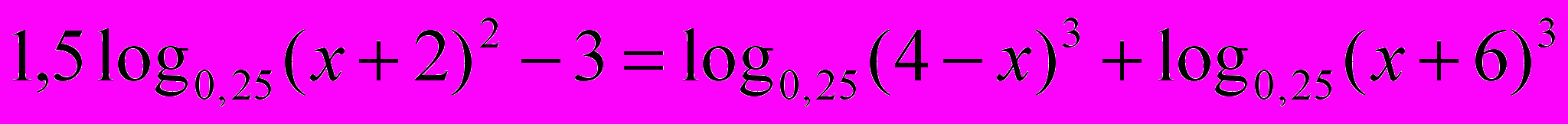
Ответ:


Самостоятельная работа:

Вариант 1 Решить уравнение: log2(x-3) = 4 (ответ: x=19). Найти произведение корней: lg2x - lgx=0 (ответ: x=10). Решить уравнение: log3(2x + 8) = log3(x - 2) (ответ: решения нет).

Вариант 2 Решить уравнение: log2(5 - x) = 2  (ответ: x=-4). Найти произведение корней: lg2x + lgx = 0 (ответ: x=0,1). Решить уравнение: log4(3x - 4) = log4(6 + x) (ответ: x=5).

Барометр настроения: Поставь крестик, как ты провел урок:








Домашнее задание: составить памятку, в которой отразить все методы

решения логарифмических уравнений, привести пример на каждый метод.


Хочется закончить урок такими словами:

Музыка может возвышать или умиротворять душу,

Живопись – радовать глаз,

Поэзия - пробуждать чувства,

Философия – удовлетворять потребности разума,

Инженерное дело – совершенствовать материальную сторону жизни людей,

а математика способна достичь всех этих целей

американский математик Морис Клайн.


Оценочный лист учащегося


Фамилия

Имя

Умения	Моя оценка	Оценка учителя
1. Находить значение логарифма
2. Находить область определения логарифмических уравнений
3. Определять методы решения логарифмических уравнений
4. Применять методы решения логарифмических уравнений в практических задачах.
5. Работать в группе
6. Анализировать свою работу на уроке

Барометр настроения









Задания для групп.


Перед вами 6 уравнений определите метод решения каждого уравнения и решите любые 3 уравнения.

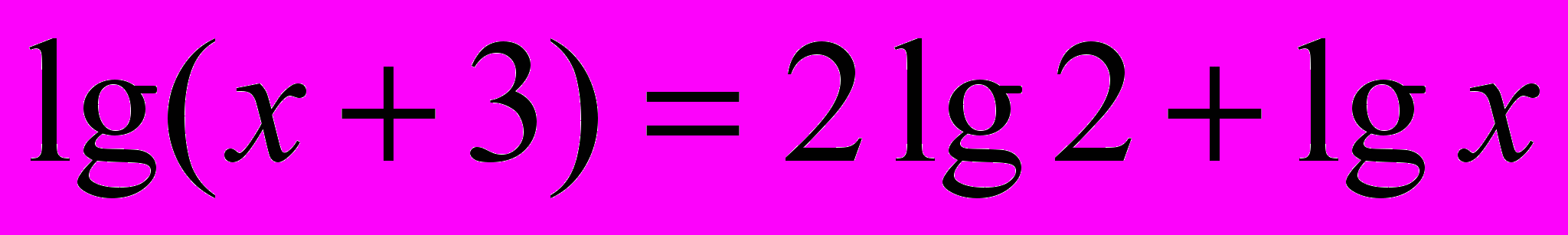
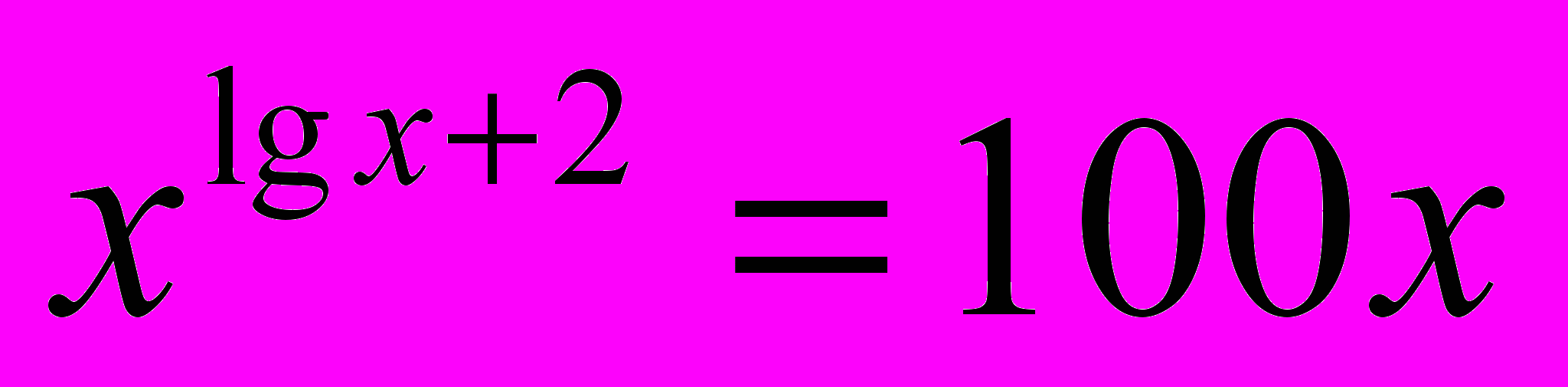
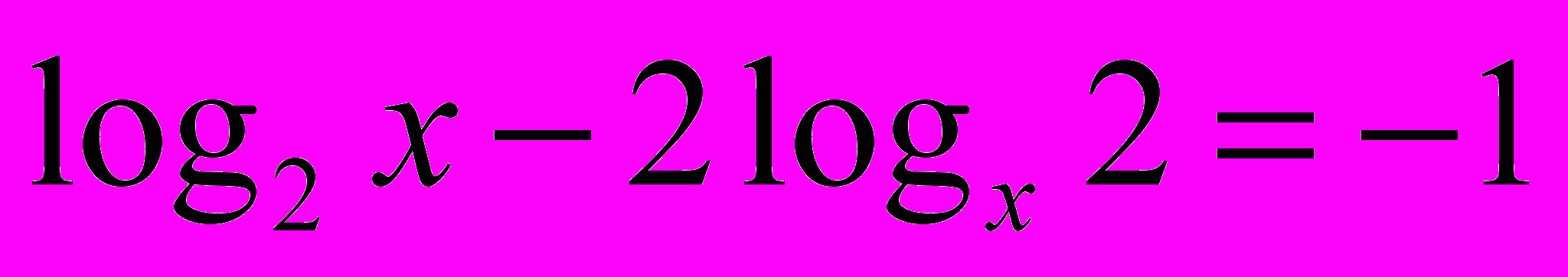
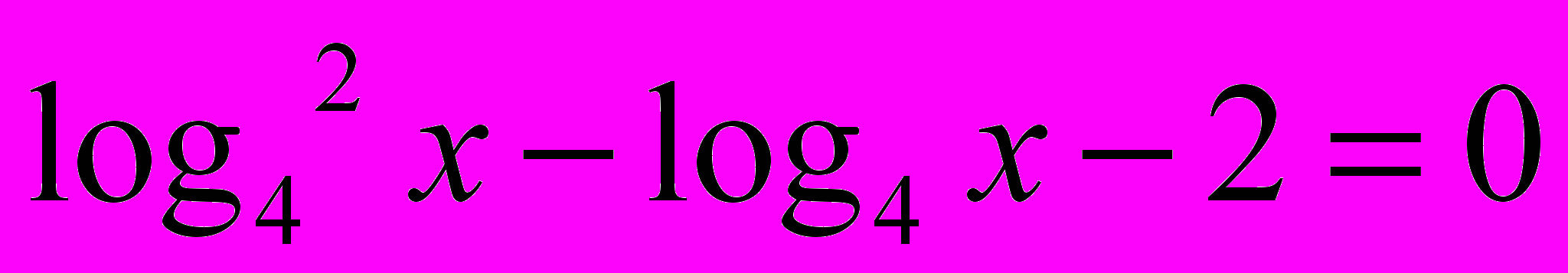
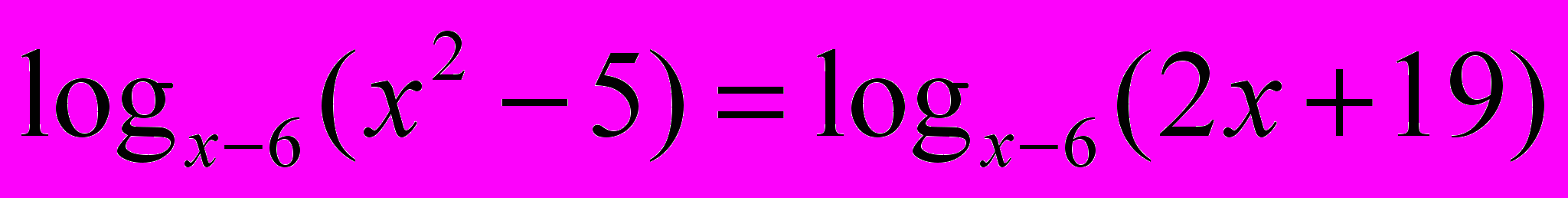
	1	2	3	4	5	6	7
A	log416	Log327	log5125	log232	log39	log28	log381
B	log25125	log4 8	log279	log816	log8127	log324	log168
C	log82	log49 7	log162	log273	log1255	log644	log322
D	log66	log55	lg10	log77	log99	log42	log24
E	lg0,01	lg0,1	lg0,001	lg1000	lg	7log73	2log25

-3	5	3	1/2	1/5	1	3/4
О	Ж	Д	Н	Р	П	Е