Шмидта Российской Академии Наук (ифз ран) по адресу; Москва 123995, ул. Большая Грузинская, д. 10. Сдиссертацией можно ознакомиться в библиотеке Учреждения ран институте физики Земли им. О. Ю. Шмидта ран автореферат
| Вид материала | Автореферат |
СодержаниеU, ускорения свободного падения g |
- Российской Академии Наук по адресу: 199034, Санкт-Петербург, наб. Макарова, д. 4 Сдиссертацией, 670.13kb.
- Тепло-электродинамические механизмы макроскопического формирования сверхпроводящих, 2637.04kb.
- Правительстве Российской Федерации по адресу: 117218, г. Москва, ул. Большая Черемушкинская,, 389.57kb.
- Аппаратная инфраструктура измерительных и управляющих систем плазменных установок ияф, 734.94kb.
- Российской Медицинской Академии последипломного образования по адресу: 123995, г. Москва,, 527.38kb.
- Кузнечные изделия населения северо-западной сибири во II-XVII веках, 271.12kb.
- Молекулярно-генетическая характеристика индивидуального района интеркалярного гетерохроматина, 399.53kb.
- Учреждения Российской Академии наук Института философии ран автореферат, 486.97kb.
- Президента Российской Федерации (по адресу: 103875, Москва, ул. Воздвиженка, д ) Сдиссертацией, 601.79kb.
- Российская дипломатия и корея (1876-1898), 662.43kb.
Методы представления решения дифференциальных уравнений или систем дифференциальных уравнений в виде ряда, обычно по времени, широко распространенный инструмент исследования дифференциальных уравнений, возникающих в геофизике. Методы построения решения в виде асимптотических разложений являются эффективным инструментом построения и анализа решений дифференциальных уравнений, однако, существуют классы задач, в которых в уравнениях или в граничных условиях присутствует малый параметр, что приводит к непригодности на больших временах решений, полученных с помощью прямых асимптотических разложений по времени [Найфе, 1976]. В задачах, содержащих малый параметр, метод построения решений в виде разложений по малому параметру, асимптотических пригодных на всем диапазоне рассматриваемого времени, представляет собой одно из наиболее мощных средств современной прикладной математики [Коул, 1972; Найфе, 1976; Бетчелор, 1973]. Этот метод позволяет получать аналитические представления решений сложных линейных и нелинейных краевых задач, которые являются равномерно пригодными по времени, то есть справедливыми и на больших временах исследуемой задачи, как для обыкновенных дифференциальных уравнений, так и для уравнений в частных производных. Аналитические методы малого параметра черезвычайно важны в многопараметрических нестационарных задачах, где нахождение характерного масштаба времени уравнений или системы уравнений , и сопоставление его с характерным временем изменения граничных условий или роста области может выявить принципиальные особенности поведения решения, выявить особые точки и асимптотики, и, тем самым, даст возможность сформулировать закономерности появления различных режимов поведения решения и увидеть их характерные свойства. Зачастую только аналитический анализ позволяет достоверно выявить закономерности поведения решения в зависимости от входящих коэффициентов и граничных условий. Для их обнаружения в численных расчетах требуется перебор большого количества вариантов расчетов. Методы построения равномерно пригодных асимптотических разложений были развиты как раз для решений задач с малыми параметрами, поскольку присутствие в задаче разных масштабов в прямом численном счете могло приводить к потере информации и затруднять или делать невозможным выявление характерных свойств решений на интересующих временах, как на малых, так и на больших. Ниже приводится построение асимптотического решения задачи о течении свободного флюида в вязкодеформируемой пористой среде с подвижной границей полученное с использованием идей построения равномерно пригодных асимптотических решений для дифференциальных уравнений с малым параметром [Коул, 1972; Найфе, 1976; Бэтчелор, 1973].
3.1 Математическая постановка задачи и решение.
Одномерное течение флюида, для которого определяющие величины будут обозначаться нижним индексом f, в пористой вязкодеформируемой среде описывается уравнениями неразрывности для флюида и матрицы, уравнением Дарси, определяющим движение флюида относительно матрицы, уравнением движения сильновязкой матрицы, а также динамическим соотношением между давлением флюида и эффективным давлением матрицы. Так как целью анализа является исследование процесса уплотнения и формирования порового давления на больших временах, где, как было показано ранее, вязкие процессы доминируют, то рассматривается вязкая постановка. Управляющая система уравнений записывается как :
 (3.1)
(3.1)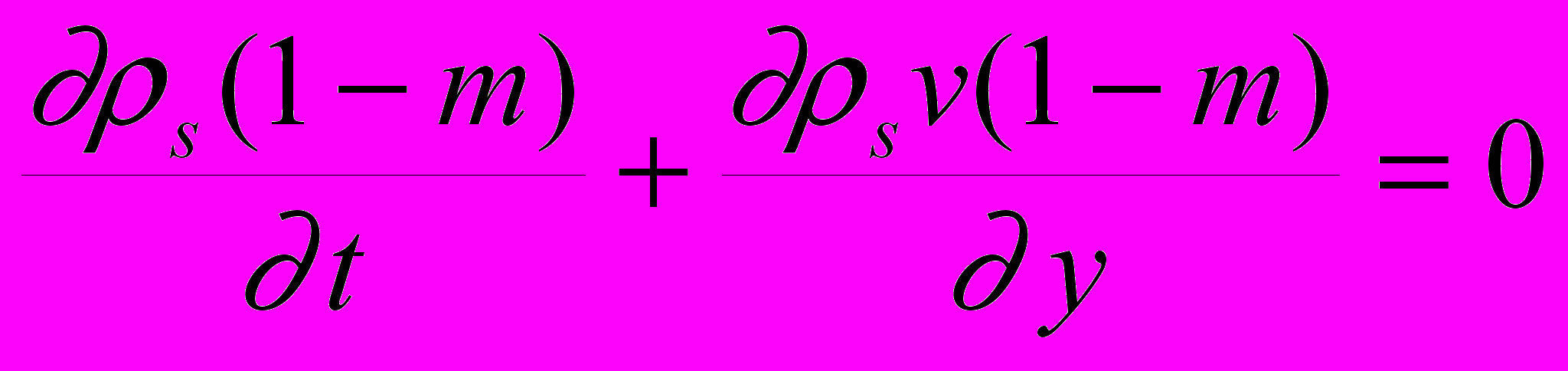 (3.2)
(3.2)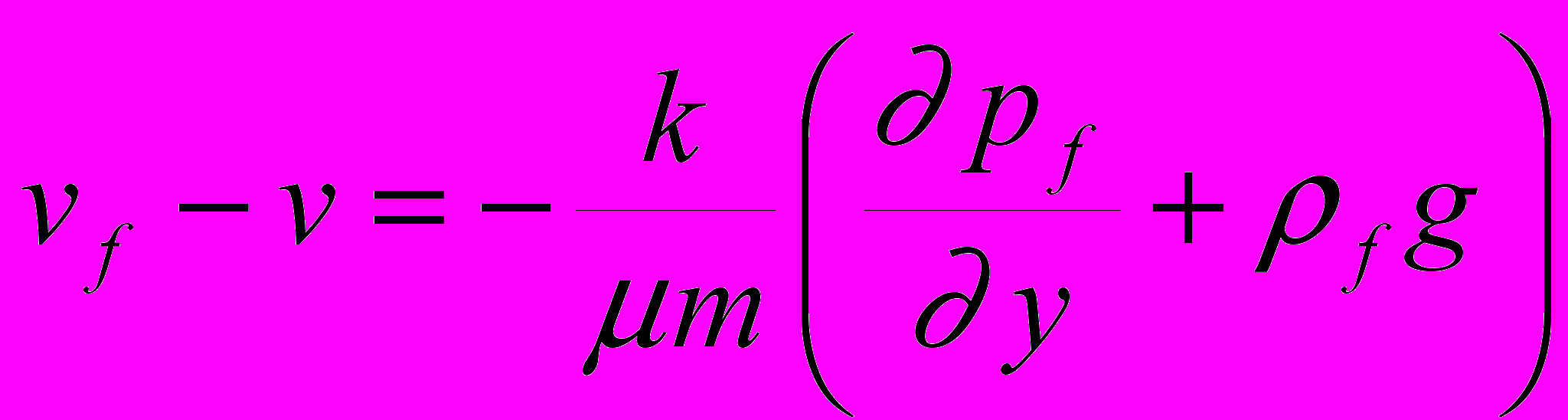 (3.3)
(3.3)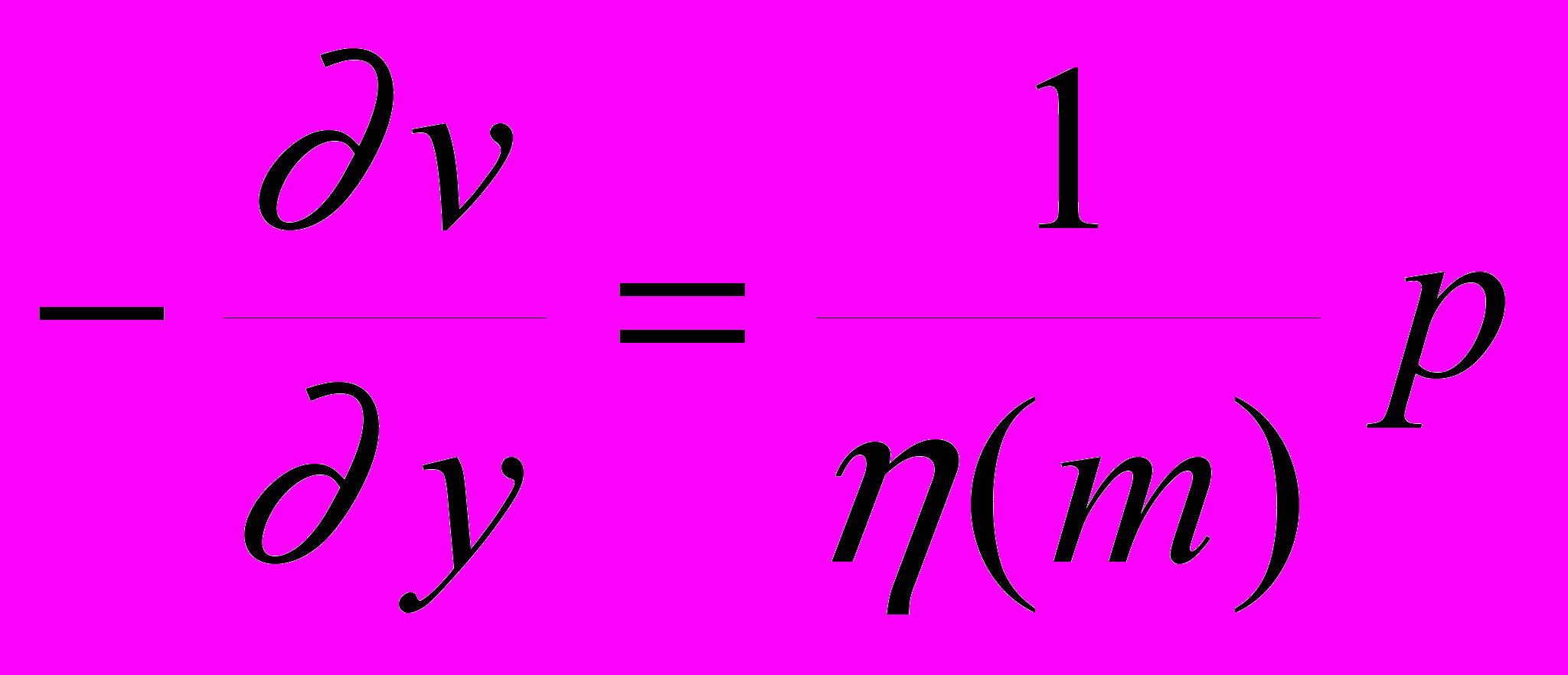 (3.4)
(3.4) p= -(ρf + Δρ)gy-pf (3.5)
Здесь используются следующие обозначения для неизвестных
величин: m - пористость, v - скорость, p – эффективное давление; для параметров:
ρ - плотность, η- вязкость среды, μ – вязкость флюида, k - проницаемость, g - ускорение свободного падения и для независимых переменных: времени - t и вертикальной координаты с положительным направлением вверх - y. Следуя изложенной в главе 2 постановке задачи накопления и уплотнения осадков, требуем, 1) чтобы уравнения (3.1-3.5) удовлетворялись в области, заключенной между нижней границей y=0 и верхней границей y=Ut, движущейся вверх с постоянной скоростью U, 2) чтобы неподвижная нижняя граница являлась непроницаемой и на ней скорости флюида и матрицы равнялись бы нулю и 3) чтобы на верхней границе пористость и давление были бы равны заданным постоянным значениям.
y=0: v f =0 , v=0 (3.6)
y=Ut: m=M, p=0 (3.7)
Соотношения (3.1) - (3.7), согласно вышеизложенному, представляют полную
формулировку задачи. В соответствии с изложенными ранее геофизическими представлениями принимается , что вязкость среды и проницаемость являются функциями пористости.
Система уравнений (3.1) - (3.5) заметно упрощается при использовании обычного предположения теории пористых сред: m<<1. Из уравнений (3.1), (3.2) и условий на границе (3.6), (3.7) следует интеграл
mvf +(1-m)v=0 (3.8)
Подстановка выражения для давления флюида pf из (3.5) в уравнение (3.2) с учетом соотношения . (3.8), приводит к системе уравнений
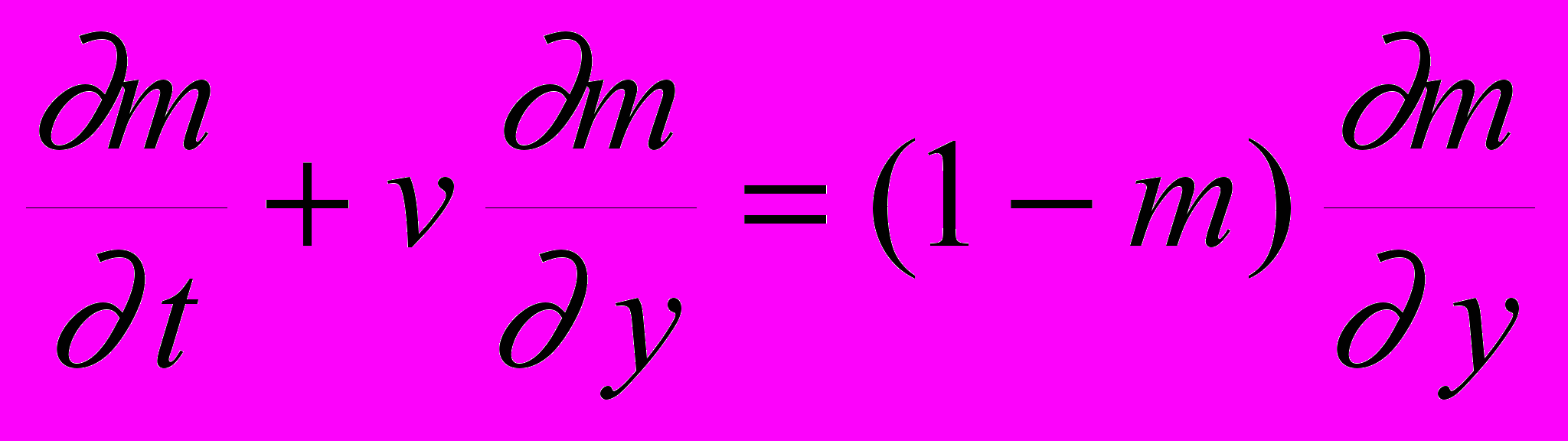 (3.9)
(3.9) (3.10)
(3.10)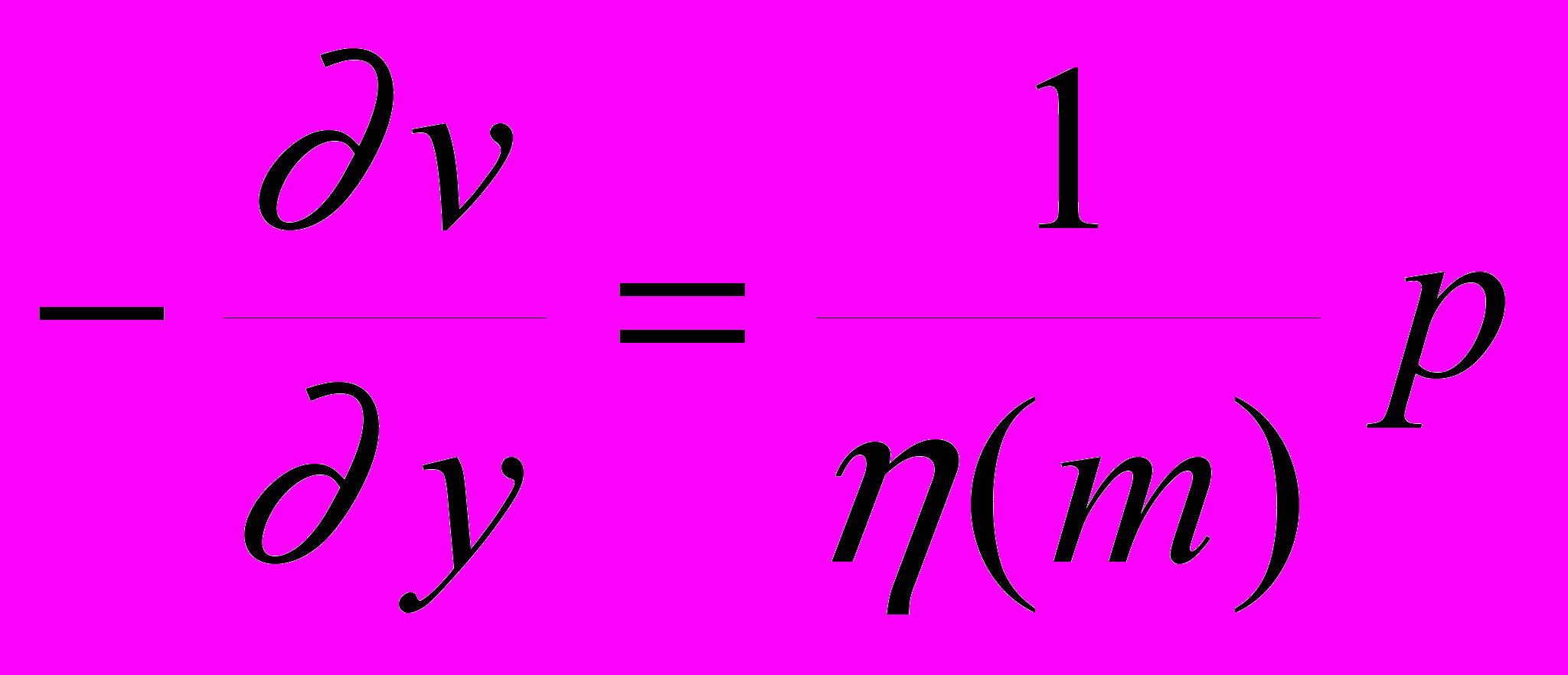 (3.11)
(3.11)с краевыми условиями
y=0: v f =0 , v=0 (3.12)
y=Ut: m=M, p=0 (3.13)
Решив задачу (3.9-3.13) можно определить скорость и давление флюида из соотношений (3.1) и (3.5)
Параметры задачи.
В соответствие с современным состоянием геофизических исследований и в зависимости от конкретного бассейна исходные параметры задачи могут варьироваться в широких пределах, некоторые величины в интервале до двух порядков. Cледуя изложеному в предыдущей части, выбираем функции k(m)=k0*ml и η(m)=η0/md, при l=2, d=1 и характерные значения в единицах СИ:
0.1<M<0.2, E-12<U
Масштабирование.
Введем характерные масштабы с помощью величин: скорости движения границы U, ускорения свободного падения g, разности плотностей матрицы и флюида ρ-ρf, а также пористости на верхней границе M. Определим масштабы длины, давления и времени, соответственно, в виде L=(η0U/g(ρ-ρf))1/2, P=(ρ-ρf)gL, T=L/U. Величины, измеряемые в этих масштабах, связаны с исходными величинами соотношениями
y=Ly`, t=Tt`, m=Mm`, v=MUv`, p=Pp`, ε=μU/(k0(ρ-ρf)gM)
В новых переменных, у которых для краткости записи опущены штрихи, задача при t>>1 записывается в виде
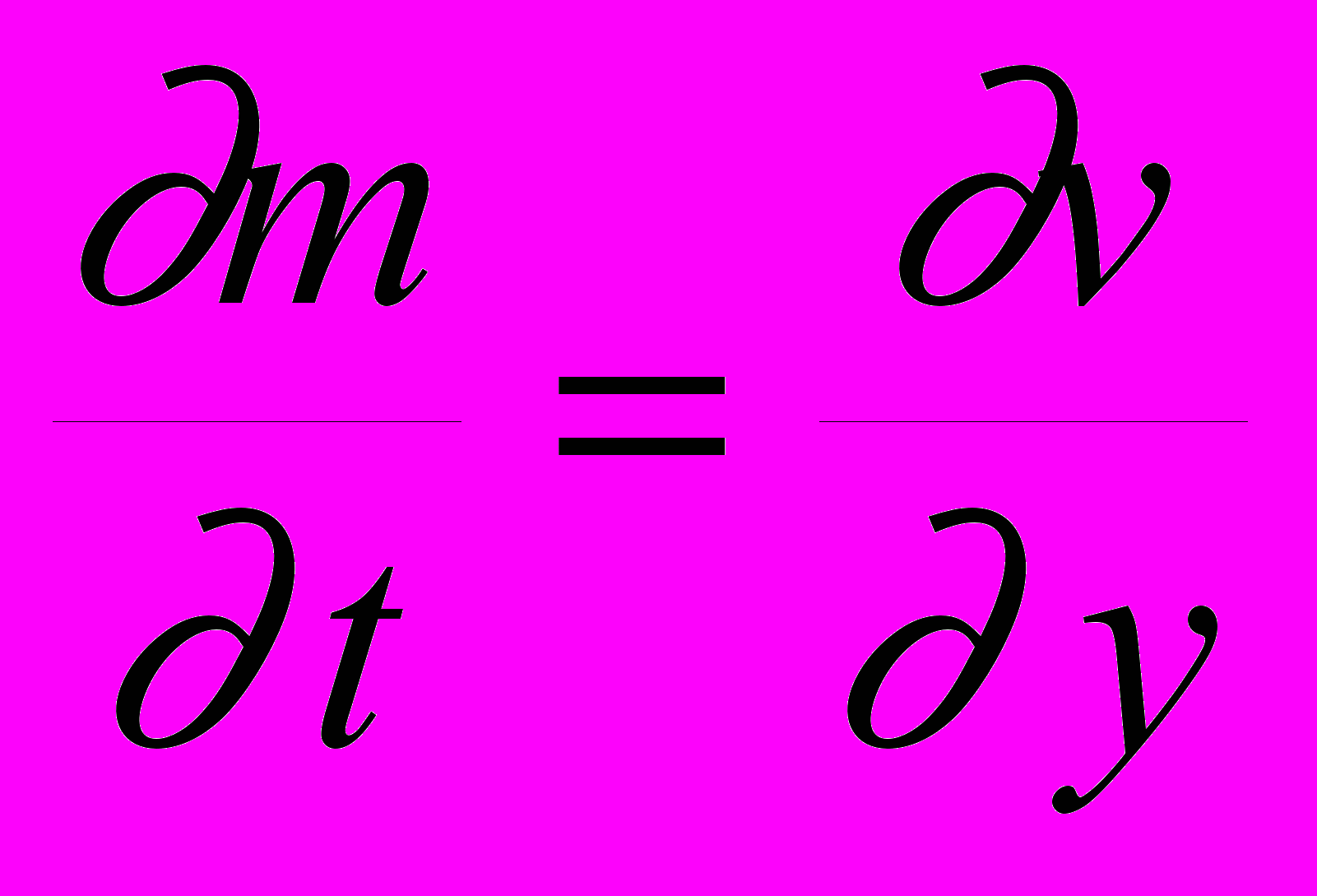 (3.14)
(3.14)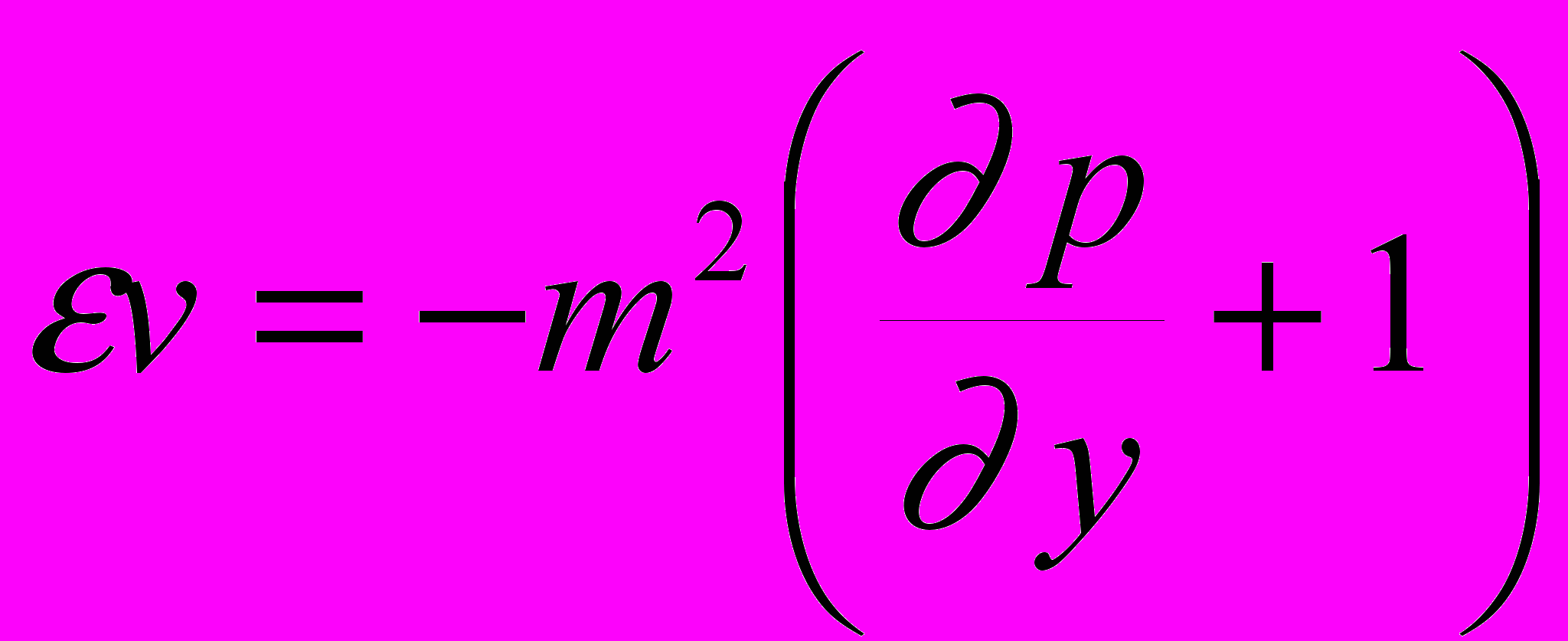 (3.15)
(3.15)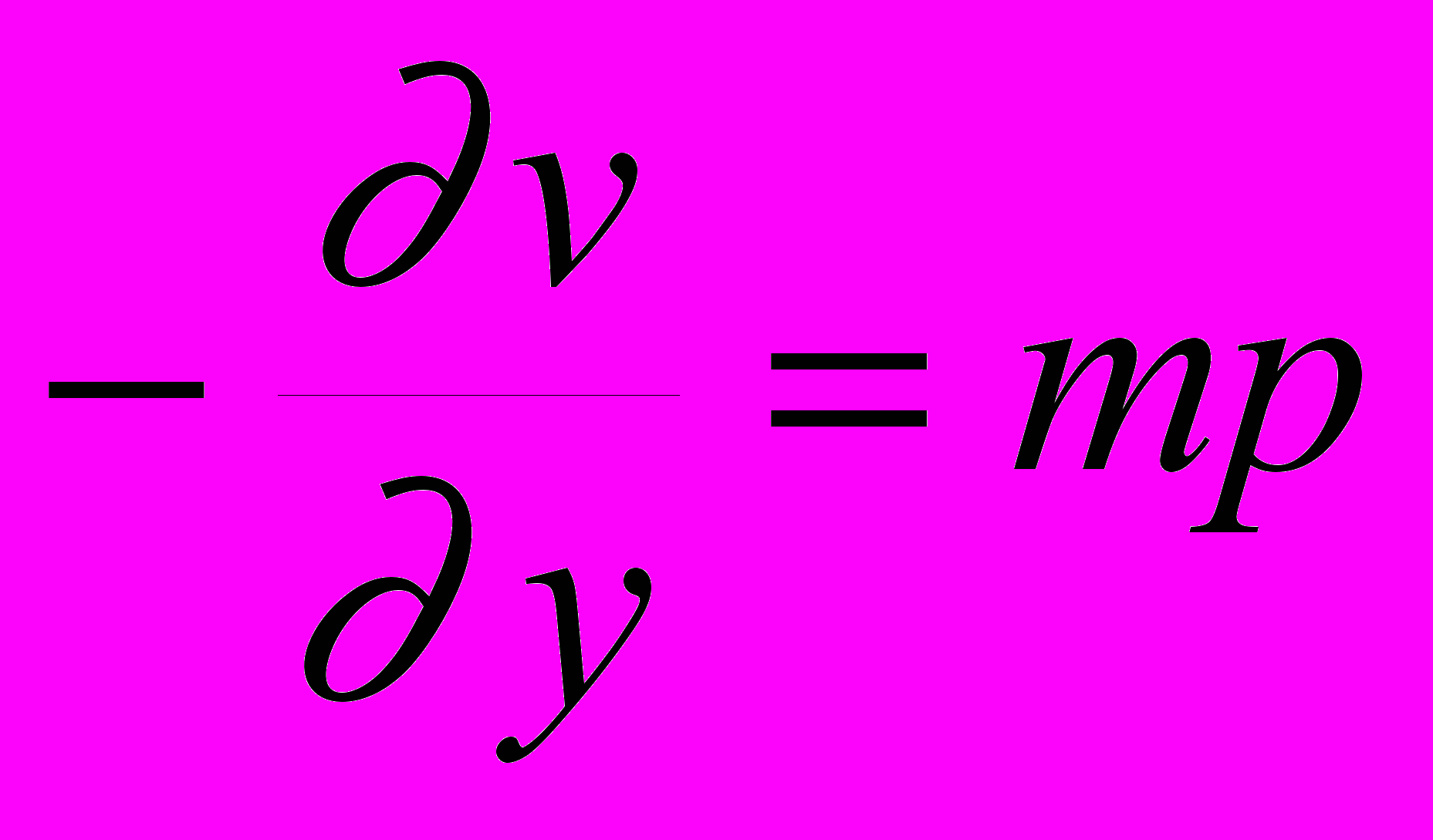 (3.16)
(3.16)с краевыми условиями
y=0 :v=0 ; (3.17)
y=t: m=1, p=0 (3.18)
Величина ε, оцениваемая по значениям исходных данных, оказывается заключенной в интервале 0.8E-5<ε<1.6E-2 и во всяком случае можно считать, что ε<<1.
Решение при ε <<1.
Представим решение s=m,v,p в виде асимптотического ряда по степеням ε
s=s0+ε•s1+... (3.19)
Подставляя разложение (3.19) в задачу (3.14-3.18 ), и ограничиваясь нулевым приближением, получаем аппроксимацию решения в виде
p0 = t-y
m0 = exp(-0.5(y-t)2) (3.20)
v0 = -m0 + exp(-0.5t2)
Решение (3.20 ) уравнений (3.14-3.16) при ε=0 удовлетворяет краевым условиям (3.17-3.18)) , но не является равномерной аппроксимацией при ε не равном 0 и t>>1. Для того, чтобы убедиться в этом, рассмотрим уравнение (3.15)) в следующем приближении - порядка ε, в котором оно записывается как
∂p1/∂y = -v0/m02 (3.21)
Если правая часть (3.21) оказывается величиной порядка 1/ε, то величина ε*p1 не является асимптотически малой по сравнению с p0 и разложение (3.19 ) неравномерно. При t>>1 и /y-t/~t значения величины m0~ε, и v0~ε, и правая часть (3.21) оценивается как ~ 1/ε. Таким образом, решение (3.20 ) является нулевым приближением внешнего разложения по ε задачи (3.14-3.18), которое аппроксимирует точное решение вблизи верхней границы, пока пористость остается величиной порядка единицы и следовательно, необходимо построить соответствующее решение вблизи нижней границы и произвести процедуру сращивания (сшивания) решения. Исходя из предыдущих оценок, следуя теории [Коул, 1972; Найфе, 1976], для нахождения решения введем новые масштабированные переменные
ti = t, yi = y/t, m=ε•mi, v=ε•vi, p=pi/t , (3.22)
которым соответствует преобразование
∂/∂y = 1/t1•∂/∂y1, ∂/∂t = ∂/∂t1 -y1/t1•∂/∂y1. (3.23)
Подставив (3.22-3.23), в уравнения (3.14 - 3.16 ), получим систему
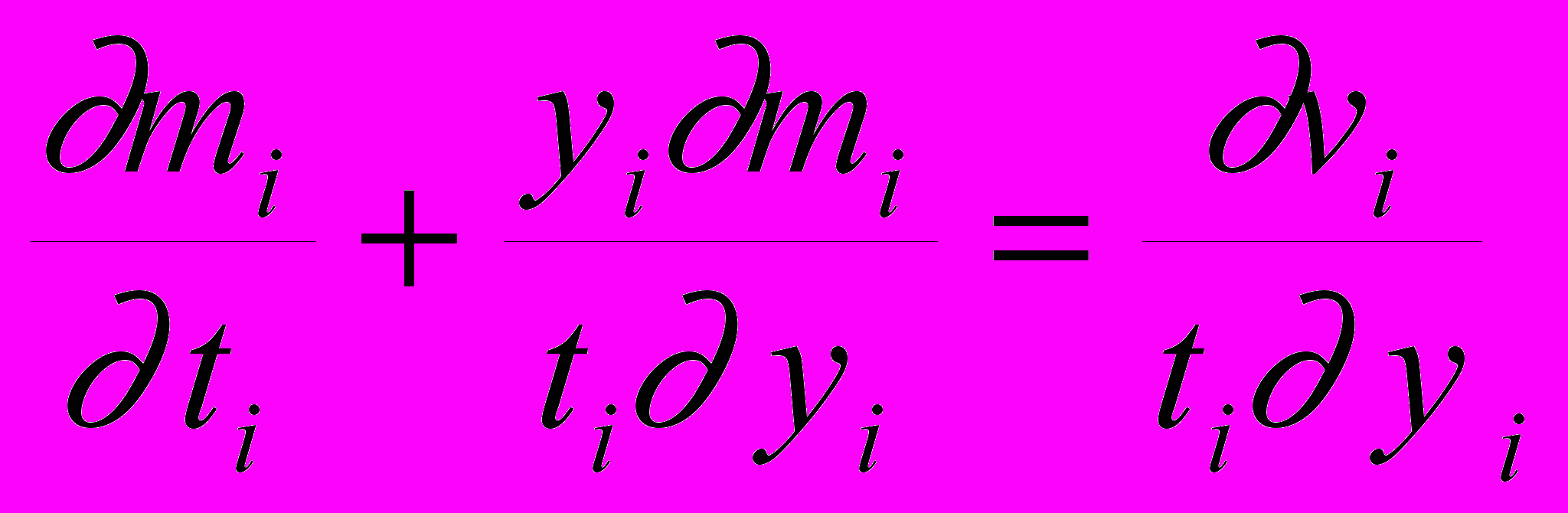 (3.24 )
(3.24 )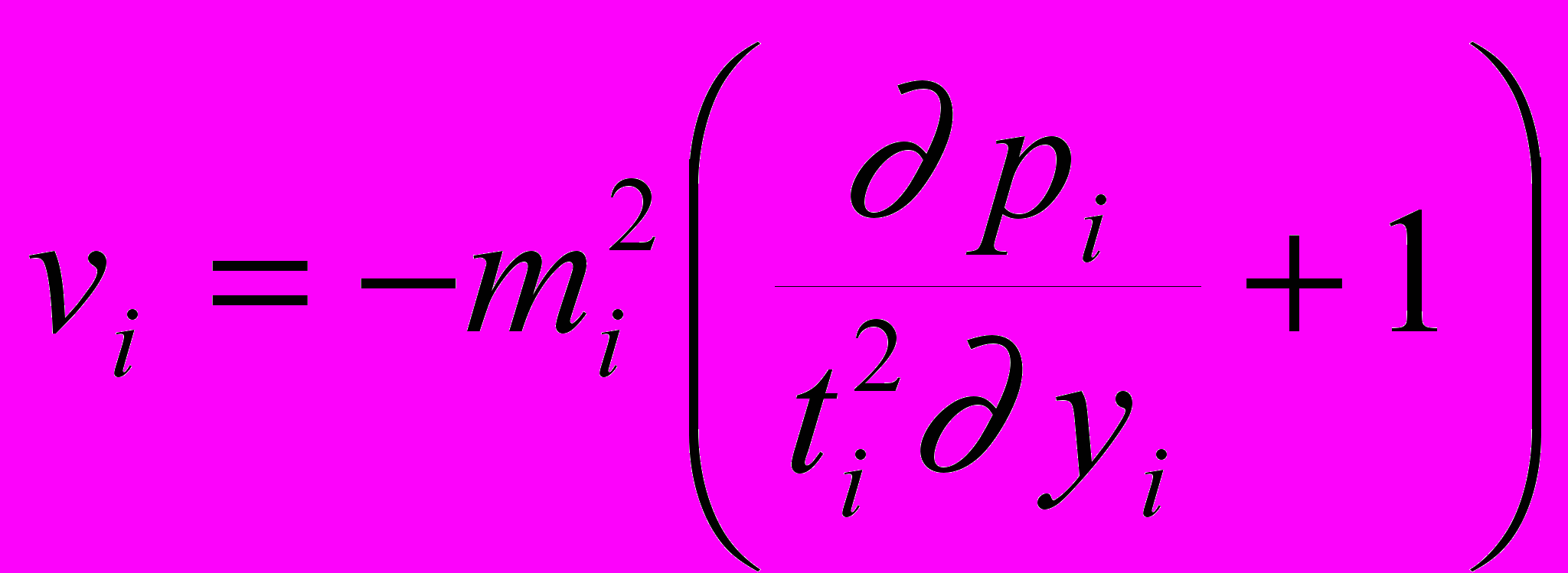 (3.25 )
(3.25 ) 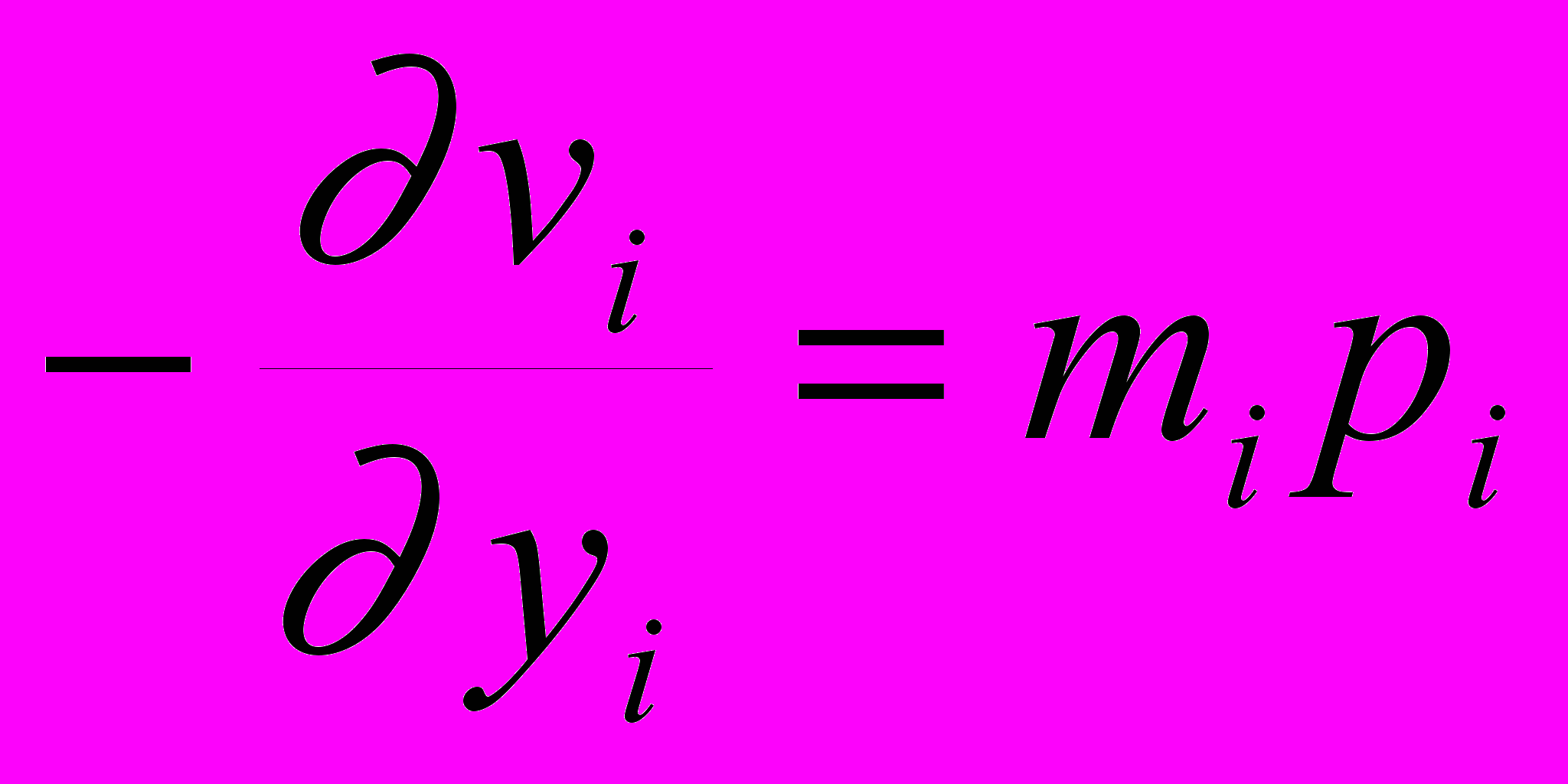 (3.26 )
(3.26 )которая имеет решение, записываемое в неявном виде
y1 = 2m1 + f(m1)/t1
v1 = -m12 (3.27 )
p1= -∂Ln(m1)/∂t1
Здесь f(mi) - неизвестная функция, которая должна быть определена из сращивания с внешним решением. Процедура сращивания внешнего (при большой пористости) и внутреннего (в окрестности нижней границы при малой пористости) решений состоит в определении функции f(mi), обеспечивающей удовлетворение решением граничных условий. Перепишем выражения для пористости в (3.20 ) и (3. 27 ) , соответственно, в виде:
y-t = - Ln 1/2(1/m2) (3.28 )
y-t = (2m1-1)t + f(mi) (3.29 )
Во внутреннем пределе при ε<<1, m1~1, с учетом связи (3.22 ), выражение (3.28 ) принимает вид
y-t = - lim Ln1/2(1/(ε•mi) 2) (3.30 )
Приравнивая (3.30 12``) и (3.29 16`), в главном приближении по ε имеем промежуточный предел m1 = 1/2 и можем определить неизвестную функцию f(mi) = - δ, где δ= Ln 1/2(4/ε2) . Теперь внутреннее решение - зависимость (3.29 ) - можно разрешить в явном виде относительно mi
m1 = 1/2 + (y-t+δ)/2t (3.31)
Срощенное выражение для пористости получаем складывая (3.31) с (3.20 ) и вычитая промежуточный предел и подставляя mi из (3.22) . Давление и скорости матрицы и флюида определяются, соответственно, из соотношений (3.16), (3.14 ) с условием (3.17 , 3.8 ), так что
m = exp(-0.5(y-t)2 ) + ε/2•(y-t+δ)/t
p = ((t-y)exp(-0.5(y-t) 2)+ ε/2•(y+δ)/t2)) /m
v = -exp(-0.5(y-t)2 ) - ε/4•(y2+2δy)/t2 + exp(-0.5t2 ) (3.32 )
vf = -v/m
Выражения (3.32) получены в нулевом приближении по ε и решения для пористости и скоростей являются равномерно пригодными по времени. Поэтому в этом приближении их можно упростить, опустив слагаемое с коэффициентом ε и окончательно решение записывается как :
m = exp(-0.5(y-t)2)
p = ((t-y)exp(-0.5(y-t)2) + ε/2•(y+δ)/t2)) / (exp(-0.5(y-t)2 ) + ε/2•(y-t+δ)/t)
v = -exp(-0.5(y-t)2) + exp(-0.5t2) (3.33)
vf = -v/m
Из выражений для скоростей флюида и матрицы видно, что толщина слоя ненулевой (порядка 1) пористости примыкает к верхней границе области течения, и ее мощность составляет величину порядка δ= ℓn 1/2(4/ε2) . Таким образом, получены аналитические равномерно пригодные асимптотические решения задачи вязкого уплотнения пористой среды растущей мощности.
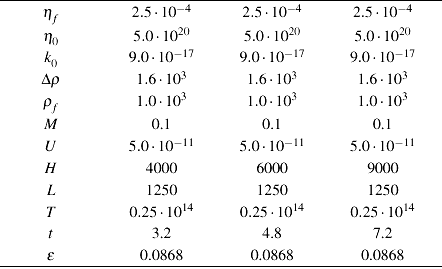
На рисунках 3.1-3.3 приводятся результаты асимптотического и численного решений для трех вариантов исходных значений параметров и соответствующих им характерных величин в единицах СИ, собранных в таблице 1. Здесь же приведены безразмерные значения времени t и параметра ε.
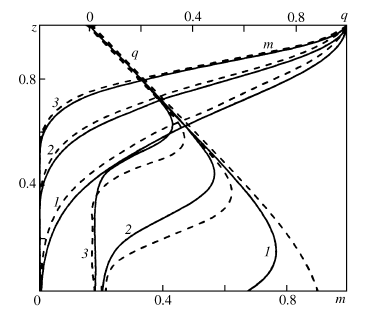
Рис. 3.1. Численное (штриховые кривые) и аналитическое (сплошные кривые) решения для пористости и эффективного давления q(z) при t=3,2; 4,8; 7,2 (кривые 1-3) и ε=0,00868 (q=pH/L)
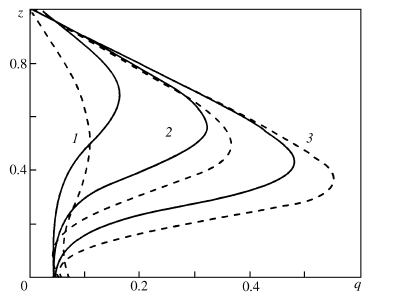
Рис. 3.2. Эффективное давление q(z) при t=4,8;и ε=0,868; 0,0868; 0,00868 (1-3)
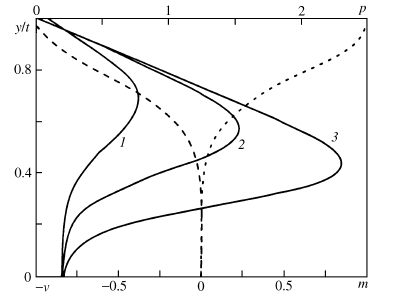
Рис. 3.3. Пористость (пунктирная кривая), скорость матрицы (штриховая кривая) и эффективное давление (сплошная кривая) при t= 4,8; и ε=0,868; 0,0868; 0,00868 (1-3)
Таблица 1
Все единицы указаны в системе СИ
Сравнение результатов, полученных асимптотическими методами, с результатами численного решения показывает удовлетворительное совпадение результатов для умеренных значений времени и хорошее - для больших, для типичных значений параметров осадконакопления. Важным обстоятельством является простота полученного асимптотического решения, делающая возможным определение пористости, давления, скоростей для конкретных геологических условий и вариаций параметров задачи с помощью достаточно простых вычислений по полученным формулам. Асимптотическое решение позволяет уверенно определить закономерность увеличения развивающегося в порах давления при увеличении значения параметра ε= μU/(k0(ρ-ρf)gM). Действительно, при увеличении значения ε знаменатель в выражении для эффективного давления (3.32, 3.33 ) растет быстрее, чем числитель, и следовательно эффективное давление уменьшается (рис.3.3 ), что, в силу определения эффективного давления, означает увеличение давления флюида. Чем больше ε , тем меньше мощность приповерхностного погранслоя в котором осуществляется основное, значимое падение пористости и тем больше градиент порового давления в приповерхностном погранслое.
Вычисляя параметры T и ε и пользуясь описанными закономерностями, можно делать обоснованные предположения о скорости падения пористости и росте порового давления с глубиной. Параметр ε интерпретируется как отношение скорости роста мощности осадочного слоя к гидродинамическому масштабу задачи, характеризующему комплекс управляющих гидродинамических параметров процесса фильтрации. Следует отметить, что параметры V и ε отличаются множителем М2, что связано с различным выбором шкал скорости и различными принятыми зависимостями проницаемости от пористости, но закономерность увеличения значения градиента давления флюида с ростом V или ε прослеживается достоверно аналитически и численно.
Таким образом, аналитическими и численными методами исследования показано, что значение формирующегося в осадках порового давления зависит от значения безразмерного параметра подобия, являющегося определенной нелинейной комбинацией физических и гидродинамических свойств осадков и скорости их накопления. Полученные результаты исследования дают возможность рассчитывать предполагаемые сценарии формирования аномально высоких давлений флюида в осадках, предсказание которых представляет теоретическую и практическую проблемы при изучении осадочных бассейнов [ Аникеев, 1971; Gretener, Feng, 1985; Фертль, 1980].
Глава 4. Исследование влияния уплотнения осадков и фильтрации поровых флюидов на тепловой режим осадконакопления.
Изучение теплового режима осадочных структур в процессе их формирования имеет большое научное и практическое значение, так как температура является одним из главных параметров определяющих физико-химические процессы, протекающие в осадочных бассейнах. При формировании осадочного заполнения бассейна происходит одновременно несколько взаимосвязанных процессов: погружение основания бассейна и накопление осадков, их прогрев, уплотнение и фильтрация к поверхности поровых флюидов. Тепловой режим осадков исследовался в рамках моделирования осадочных бассейнов по двум направлениям. Первое, начатое работой McKensie, (1978), -изучение эволюции температур в осадках, обусловленной внешними, по отношению к структуре осадков, факторами, и глубинными процессами. Второе- следующее работе Birch (1968), основанное на решении тепловой задачи для однородного полупространства с стационарным распределением температуры, которое нарушается возникшим движением верхней границы. Было также получено аналитическое решение задачи о тепловом режиме осадконакопления,
учитывающее и влияние движения границы и нестационарность теплового потока, поступающего к основанию осадочного слоя [Суетнова, 1989]. Однако, вклад происходящего при накоплении осадков процесса уплотнения и связанного с ним процесса фильтрации к поверхности поровых флюидов в эволюцию температурного поля осадков был мало изучен. В работах [Hutchison, 1985; Bethke, 1985; Wangen, 1992] проводилось моделирование теплового режима осадочных бассейнов с учетом вклада фильтрации к поверхности порового флюида, однако закон фильтрации следовал из принятой модели уплотнения Ати [Athy,1930.], с заданной априори кривой убывания пористости по глубине и без рассмотрения процесса уплотнения. В настоящей работе для моделирования и анализа влияния процесса уплотнения осадков и фильтрации порового флюида на тепловой режим осадочного бассейна используется представленный в предыдущей главе подход, который дает возможность анализа влияния взаимообусловленных процессов уплотнения и фильтрации порового флюида на эволюцию во времени распределения температур в процессе формирования бассейна. Исследуется уравнение теплопроводности (2.1.5 ), с зависящей от времени и глубины скоростью массопереноса, в слое растущей толщины. Рассматриваемая задача не включает рассмотрение вклада теплогенерации осадков [Гордиенко, 2005], и зависимости тепловых свойств от PT условий [Миклашевский, Попов, и др., 2006], что, в рамках сформулированной цели исследования не снижает общности результата.
Пользуясь идеями построения равномерно пригодных асимптотических решений дифференциальных уравнений [Коул, 1972; Найфе, 1976 ] в предыдущей главе было получено выражение для асимптотического решения задачи (3.1-3.7 ), которое дает выражение для скорости фильтрации и скорости осадков в виде:
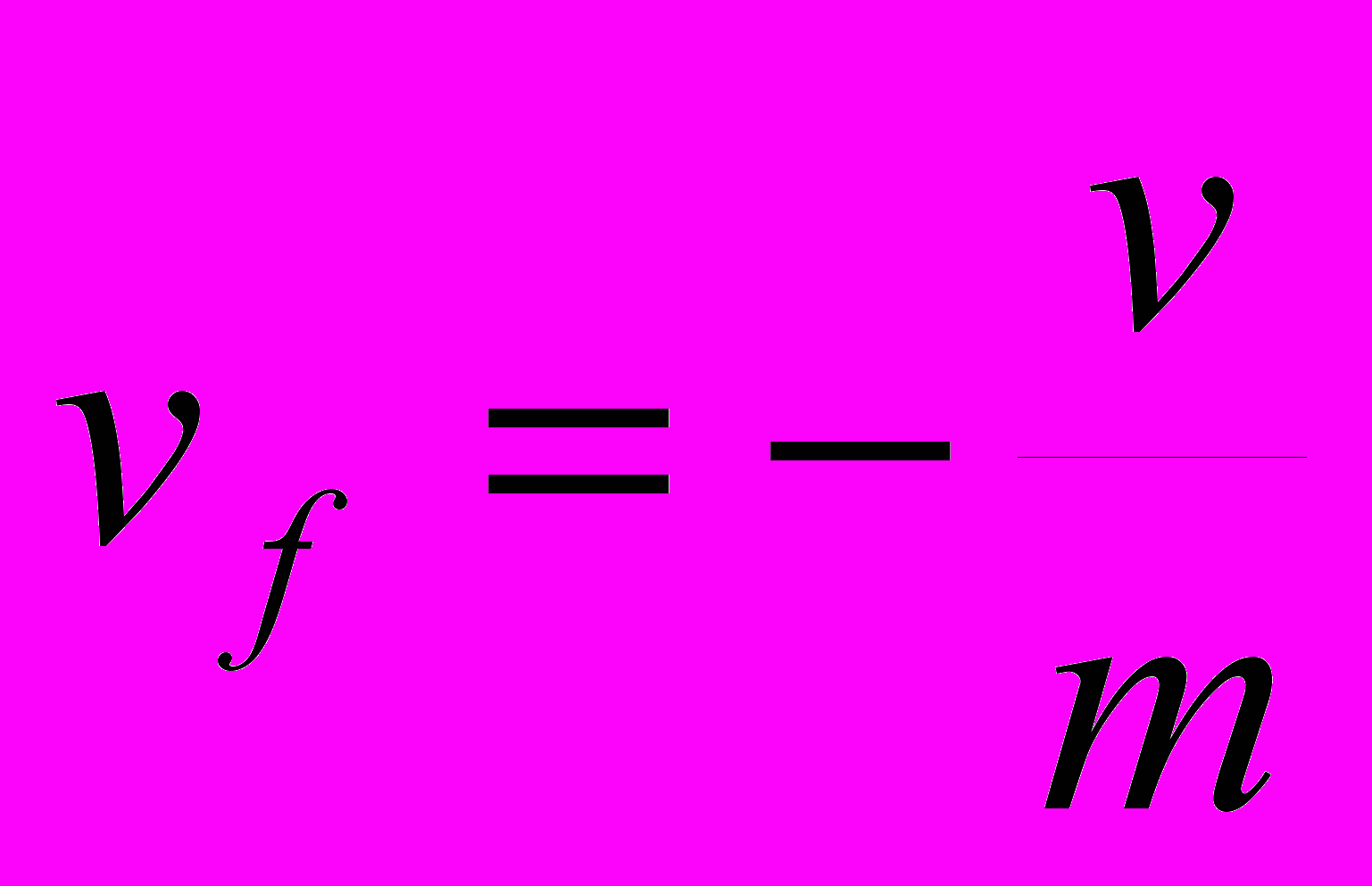
где
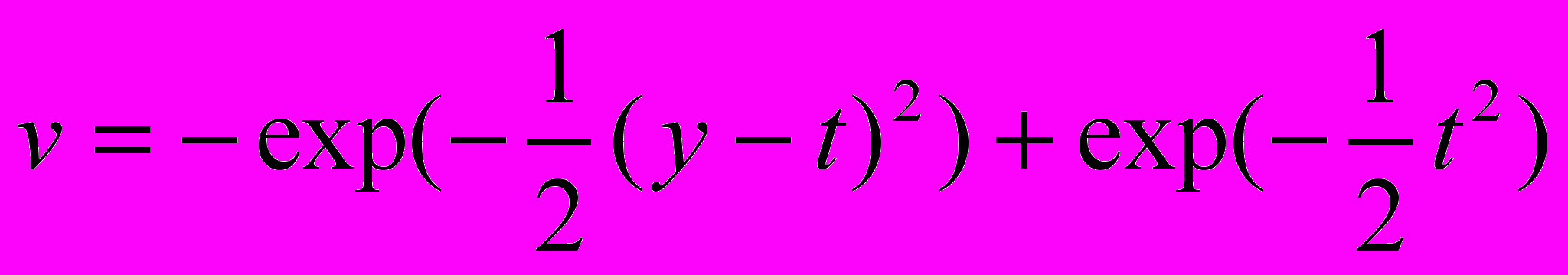 (3.33)
(3.33)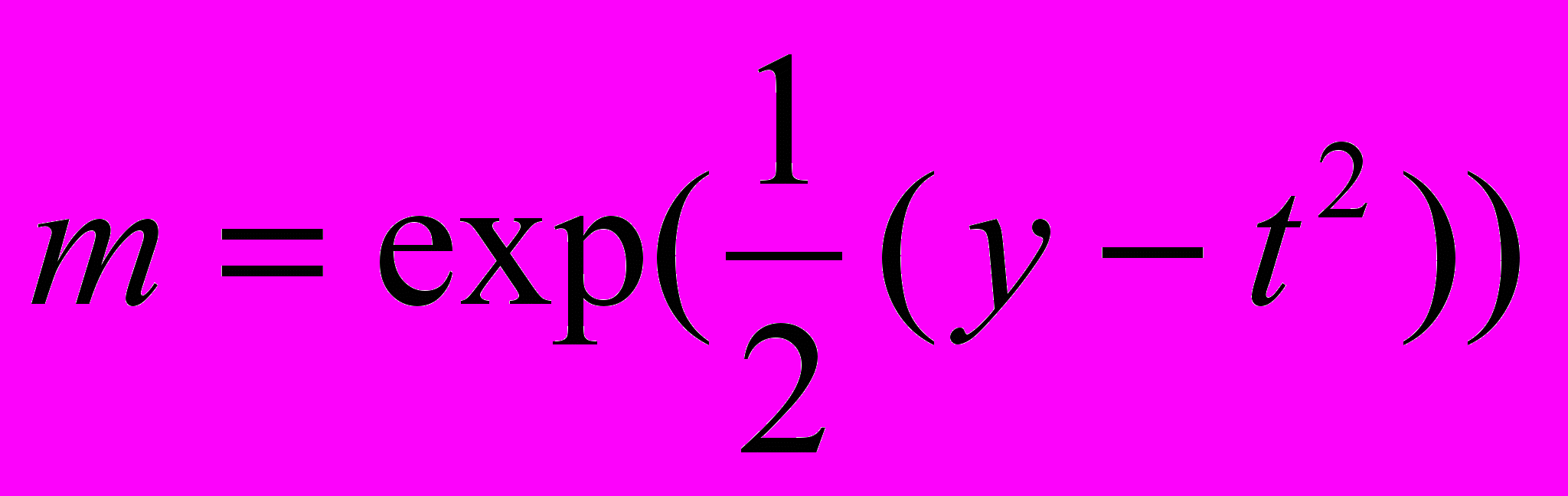
Как было показано, асимптотическое решение дает удовлетворительное совпадение с численным при умеренных временах и хорошее - при больших для реалистических параметров модели [Суетнова, Чернявский 2001 ], что дает возможность использовать его для анализа и решения уравнения теплопроводности (2.1.5). Характерные времена конвективного и кондуктивного переноса тепла сильно различаются, так как характерное время прогрева слоя осадков толщины d определяемое как d 2/K2 много меньше характерного времени накопления такого слоя при формировании бассейна d./U [Суетнова. 1989]. Поэтому, в нулевом приближении решение уравнения (2.1.5) удовлетворяет стационарному уравнению [Суетнова. 1989] и параметрически зависит от медленного времени t задачи (3.1-3.7 ). С учетом этого обстоятельства и формулы (3.8) уравнение теплопроводности (2.1.5) в безразмерных переменных и системе координат задачи (3.1-3.7 ) имеет вид:
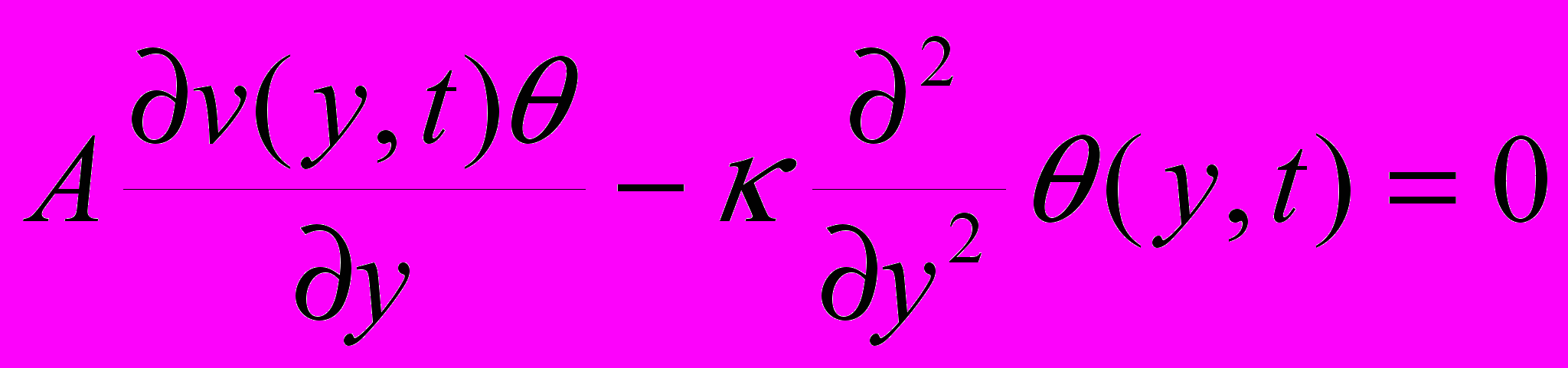 (4.1)
(4.1)A= -(A1 -A 2 )М
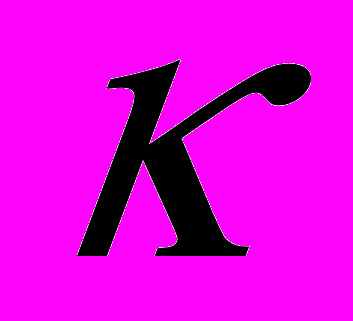 =KT/L2
=KT/L2  =f/F F=2730
=f/F F=2730Краевое условие на нижней границе определяется заданным потоком тепла, а верхняя поверхность при y=t, поддерживается при нулевой температуре.
 (4.2)
(4.2)H= BL/F
Решая (4.1 ) относительно θ с использованием (4.2) и выражения для скорости из (3.33) находим решение для температуры в виде:
 (4.3 )
(4.3 )Для представления полученных аналитических решений в численном виде брались типичные тепловые характеристики, использовавшиеся в исследованиях теплового режима осадочных бассейнов [ Hutchison, 1985; Turcotte and Schubert, 1982 ], так что для приведенных ниже графиков расчеты проводились для значений А =-0.46; К=0.4
 , F=2730K. На рисунках 4.1-4.3 приведены результаты вычислений безразмерных температуры и градиента температуры при различных значениях механических параметров задачи, соответствующих реалистическим сценариям осадконакопления. На каждом рисунке распределение соответствующей величины по глубине показано для трех моментов безразмерного времени задачи, что дает возможность проследить эволюцию распределения температуры и ее градиента в процессе роста толщины слоя осадков. На Рис.4.1. показаны распределения по глубине в различные моменты времени температуры; рассчитанные для L=3953 и T=0.79 1013 , что соответствует значению вязкости
, F=2730K. На рисунках 4.1-4.3 приведены результаты вычислений безразмерных температуры и градиента температуры при различных значениях механических параметров задачи, соответствующих реалистическим сценариям осадконакопления. На каждом рисунке распределение соответствующей величины по глубине показано для трех моментов безразмерного времени задачи, что дает возможность проследить эволюцию распределения температуры и ее градиента в процессе роста толщины слоя осадков. На Рис.4.1. показаны распределения по глубине в различные моменты времени температуры; рассчитанные для L=3953 и T=0.79 1013 , что соответствует значению вязкости  =5 1020 Па с и скорости роста мощности осадков U=5 10 –10 м./с
=5 1020 Па с и скорости роста мощности осадков U=5 10 –10 м./с.
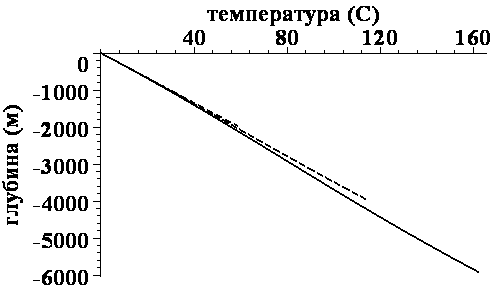
Рис.4.1 Штрих-пунктирная линия соответствует значению времени t=0.5, пунктирная линия соответствует значению времени t=1, сплошная линия соответствует значению времени t=1.5.
Из рисунка видно, как фильтрация порового флюида и уплотнение осадков влияет на распределение температуры по глубине.
Следующий рисунок (Рис.4.2 ) показывает как изменяется распределение температуры и ее градиента при большей вязкости осадков но при меньшей скорости накопления осадков, U=5 10–11 м./с., и тех же остальных параметрах задачи, что приводит к следующим значениям безразмерных величин L=3953; T=0.79 1014 .
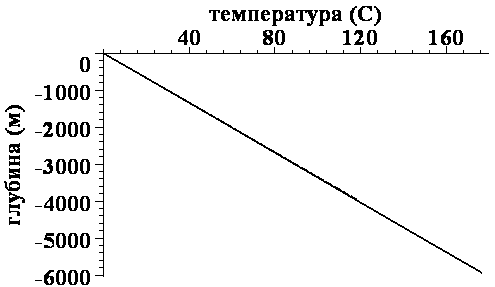
Рис.4.2 Обозначения как на рис.4.1.
Распределение температуры и ее градиента демонстрируют незначительное отклонение от линейного распределения. Расчеты наглядно показали, что уменьшение вязкости накапливающихся осадков и увеличение скорости их накопления приводит к росту нелинейности профиля температуры за счет влияния скорости накопления, уплотнения и фильтрации поровых флюидов к поверхности, вызываемой уплотнением.
Результаты моделирования теплового режима накапливающихся осадков при учете их уплотнения и обусловленной уплотнением фильтрации порового флюида к поверхности в диапазоне репрезентативных значений параметров осадконакопления показали, что влияние этих процессов на тепловой режим осадков незначительно и тем меньше, чем меньше скорость накопления осадков.
