Шмидта Российской Академии Наук (ифз ран) по адресу; Москва 123995, ул. Большая Грузинская, д. 10. Сдиссертацией можно ознакомиться в библиотеке Учреждения ран институте физики Земли им. О. Ю. Шмидта ран автореферат
| Вид материала | Автореферат |
- Российской Академии Наук по адресу: 199034, Санкт-Петербург, наб. Макарова, д. 4 Сдиссертацией, 670.13kb.
- Тепло-электродинамические механизмы макроскопического формирования сверхпроводящих, 2637.04kb.
- Правительстве Российской Федерации по адресу: 117218, г. Москва, ул. Большая Черемушкинская,, 389.57kb.
- Аппаратная инфраструктура измерительных и управляющих систем плазменных установок ияф, 734.94kb.
- Российской Медицинской Академии последипломного образования по адресу: 123995, г. Москва,, 527.38kb.
- Кузнечные изделия населения северо-западной сибири во II-XVII веках, 271.12kb.
- Молекулярно-генетическая характеристика индивидуального района интеркалярного гетерохроматина, 399.53kb.
- Учреждения Российской Академии наук Института философии ран автореферат, 486.97kb.
- Президента Российской Федерации (по адресу: 103875, Москва, ул. Воздвиженка, д ) Сдиссертацией, 601.79kb.
- Российская дипломатия и корея (1876-1898), 662.43kb.
В предыдущих главах были проанализированы фундаментальные закономерности уплотнения накапливающихся осадков для реалистических значений физических условий их накопления. Однако, эти закономерности были выявлены на основании анализа результатов моделирования процесса накопления и уплотнения однородных осадков. В описаниях истории заполнения осадочных бассейнов (по данным геофизических исследований и по данным бурения) можно увидеть, что в течении геологической истории менялись виды осадков, как например, преимущественно песчаные осадки сменялись преимущественно глинистыми, что сильно меняет гидродинамические свойства осадков [Файф, Прайс, Томпсон, 1981 ]. Моделирование процесса уплотнения осадочного слоя, история формирования которого включает периоды накопления различного осадочного материала, представляет интерес как для фундаментальной, так и для прикладной геофизики. Закономерности формирования сложных, немонотонных профилей распределения пористости и порового давления по глубине осадков могут быть исследованы с помощью математического моделирования и численных экспериментов. Математическая модель (глава 2) позволяет провести численные эксперименты, которые позволяют выявить характер влияния изменения физических характеристик поступающих осадков на процесс их уплотнения в течении осадконакопления. При моделировании задавались базовые значения вязкости и проницаемости, используемые для вычисления масштабных шкалирующих параметров и текущие значения вязкости и проницаемости, соответствующие моменту накопления, которые могли отличаться от базовых значений. На рисунке 5.1 показаны результаты расчетов эволюции распределения пористости и порового давления для случая накопления, в определенный период времени формирования бассейна, осадочного слоя меньшей, чем прилегающие слои, вязкости.

Рис.5.1 Эволюция распределения пористости а) и порового давления б) по глубине бассейна в случае накопления осадков с пониженной вязкостью в период времени, когда мощность осадочного слоя увеличивалась от 0.35 до 0.37 его конечной мощности.
Слой с меньшей вязкостью уплотняется быстрее, создавая препятствие фильтрации порового флюида к поверхности. В дальнейшем, при накоплении вышележащих слоев осадков процесс уплотнения приводит к формированию двух зон сверху и снизу слоя пониженной вязкости, в каждой из которых продолжается увеличивающееся со временем падение пористости по глубине. Поровое давление нарастает в нижней зоне быстрее, чем в верхней, что связано с быстрым падением пористости в слое пониженной вязкости (Рис 4.1б).
Другой важный пример, иллюстрирующий влияние различия вязкости поступающих в различные периоды времени осадков на эволюцию пористости и порового давления в формирующемся бассейне приведен на рисунке 5.2 а,б.
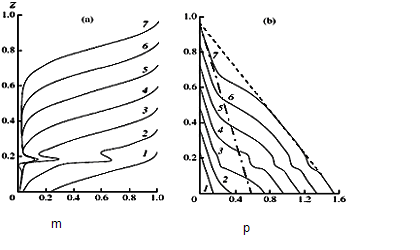
Рис.5.2 а,б. Эволюция распределения пористости а) и порового давления б) по глубине бассейна в случае накопления осадков с повышенной вязкостью в период времени, когда мощность осадочного слоя увеличивалась от 0.15 до 0.2 от его конечной мощности.
Если в процессе седиментации накапливается слой осадков с вязкостью, повышенной по сравнению с вязкостью прилегающих слоев, то, при последующем наращивании мощности осадочного слоя, также формируются верхняя и нижняя зоны прогрессивного уплотнения. Между ними, в области повышенной вязкости, тоже происходит падение пористости во времени, но более медленное так, что пористость в этой области всегда остается большей чем, чем в прилегающих зонах (Рис 5.2а). Поровое давление, развивающееся в этой области по мере роста толщины перекрывающих осадков, превышает гидростатическое, но остается всегда меньшим, чем в прилегающих слоях (Рис 5.2б).
В случае, когда при формировании бассейна накапливаются слои с различными коэффициентами проницаемости, например преимущественно глинистые сменяются преимущественно песчаными или наоборот, процесс их уплотнения приводит также к образованию относительных вариаций пористости и порового давления по глубине (Рис. 5. 3а, б ) по сравнению с базовой моделью однородного осадконакопления (Рис.2.1 а, б).
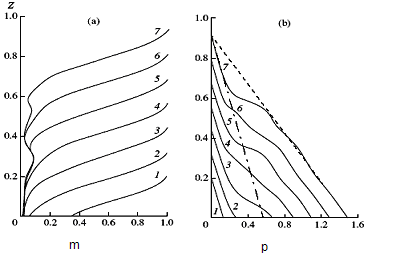
Рис 5.3 а,б эволюция распределения пористости а) и порового давления б) по глубине бассейна в случае накопления осадков с пониженной проницаемостью в периоды времени, когда мощность осадочного слоя увеличивалась от 0.25 до 0.4 и от 0.53 до 0.62 его конечной мощности. Все остальные параметры как для рис.2.1.
В слое с относительно пониженной проницаемостью падение пористости затруднено из-за относительно более быстрого падения пористости в накапливающихся вышележащих слоях большей проницаемости. При этом поровое давление, формирующееся в этом слое, превышая гидростатическое, оказывается больше, чем в случае соответствующего однородного осадконакопления. С геофизической точки зрения, интерес представляет и исследование закономерностей истории уплотнения осадков в случае длительных периодов накопления осадков с относительно пониженной проницаемостью которые в дальнейшем перекрыты более проницаемыми осадками, что может потенциально уменьшить, относительно случая накопления однородных осадков, поток порового флюида в более проницаемые вышележащие слои. На рисунке 5.4 представлены результаты расчетов эволюции распределения пористости и порового давления в истории формирования осадочного слоя финальной мощности 8 км. при накоплении осадков таким образом, что слой с относительно пониженной проницаемостью (0.1 k0) стал накапливаться с момента, когда мощность осадков составляла около 0.17 от его финальной мощности, принятой за 1, и до момента, когда мощность осадков составляла около 0.49 . После этого, верхняя часть осадочного слоя формировалась за счет накопления осадков с проницаемостью k0 . То есть, это модель процесса перекрытия менее проницаемых осадков более проницаемыми. Расчеты показывают, что перекрытие менее проницаемых осадков относительно более проницаемыми в течении формирования осадочной толщи вносит возмущения в профили распределения пористости и порового давления по глубине в различные моменты времени (рис. 5.4) по сравнению с профилями, формирующимися при накоплении осадков с постоянными гидродинамическими характеристиками.
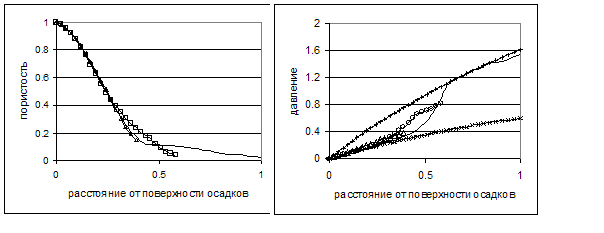
Рисунок 5.4. Распределение пористости и порового давления по глубине осадков в различные моменты истории формирования осадочного слоя, представленные в безразмерном виде.
Модельный рисунок 5.4 показывает профиль порового давления, подобный наблюденному распределению давления, приведенному в работе [Neuzil , 1995]. Результаты модельных расчетов в целом находятся в удовлетворительном соответствии с имеющимися в литературе геофизическими данными по осадочным бассейнам, что подтверждает обоснованность описываемого моделью механизма нестационарного вязкоупругого уплотнения накапливающихся осадков при последовательном накоплении слоев с различными физическими свойствами.
Представленные результаты численного моделирования нестационарного вязкоупругого уплотнения накапливающихся осадков, позволили прояснить влияния неоднородностей свойств накапливающихся осадков на процесс их уплотнения и механизм образования флуктуаций распределения пористости и порового давления по глубине осадочной толщи за время ее формирования и их эволюцию в течении истории осадконакопления. Результаты численного моделирования показывают, что накопление слоя относительно пониженной вязкости приводит в дальнейшем, со временем, к образованию и сохранению в убывающем по глубине распределении пористости инверсии, такой, что пористость ниже этого слоя оказывается большей, чем в вышележащих слоях, а поровое давление растет, стремясь к литостатическому. К формированию в глубине толщи осадков зон инверсии пористости приводит также относительно пониженная проницаемость накопившихся в определенный момент истории осадконакопления слоев осадков, при этом происходит относительное увеличение порового давления именно в этих слоях. Подобная инверсия пористости образуется и в случае накопления слоя сравнительно повышенной вязкости, однако, в этом случае, поровое давление напротив, будет иметь в этой области локальный минимум. Таким образом, предложенная модель объясняет возможные механизмы образования в толще осадков вязкоупругой реологии пористых коллекторов с принципиально разным уровнем порового давления, т.е. с локально повышенным и локально пониженным давлением относительно прилегающих слоев.
Глава 6. Анализ закономерностей взаимовлияния режима осадконакопления и уплотнения осадков и процесса осаждения примесей из насыщающего флюида на примере аккумуляции газгидратов в зоне их стабильности в субаквальных условиях.
Представленные в предыдущих главах результаты моделирования базового процесса уплотнения накапливающихся осадков могут быть использованы как основа для моделирования широкого класса задач в области изучения осадочных толщ, связанных с переносом флюидом примесей, для которых процесс их растворения и, или, осаждения зависит от температуры и давления.
Фильтрация к поверхности поровых флюидов, содержащих растворенный газ, во многих случаях, описанных в научной литературе, приводит к образованию на разных глубинах в толще осадков слоев, насыщенных газгидратами. Благоприятные для образования и стабильности газгидратов давления и температуры широко распространены в осадочных структурах океанского дна, где при условии достаточного количества термогенного или биогенного газа (в основном метана) [Троцюк, Марина, 1988 ], происходит образование гидратов глубинах [Гинсбург, Соловьев, 1994;]. Газгидраты в естественных условиях представляют собой кристаллические образования из газа (главным образом метана) и воды, подобные льду, которые стабильны в определенном диапазоне давления и температуры [Sloan, 1997]. Проведенные к настоящему времени исследования поддерживают гипотезу о образовании гидратов из биогенного и термогенного газа, который транспортируется в зону стабильности гидратов c фильтрующимся коровым флюидом [Hyndman, Davis, 1992; BenClennel, Hovland , Booth, et. al, 1999, Kleinberg еt al, 2003]. К настоящему времени различными геофизическими методами (в основном сейсмическими) выявлено более 100 площадей проявлений газгидратов в осадках [Kleinberg, Flaum, Griffin et al., 2003; Дмитриевский, Баланюк, 2006 ]. Для адекватной интерпретации данных геофизических измерений и природы сейсмических границ в земной коре [Hyndman, Yuan, Moran , 1999 ] необходимо развитие моделей образования и эволюции газгидратных проявлений в естественных условиях. В данной главе на основе численного моделирования исследуются особенности взаимного влияния процессов уплотнения субаквальных осадков и формирования в пористой среде осадков газгидратов из растворенного в коровом флюиде газа при различных режимах фильтрации насыщающего флюида флюида, определяемых проницаемостью осадков, их физическими свойствами и скоростью их накопления. В рамках разработанной комплексной математической модели характерное течение процессов уплотнения осадков, фильтрации флюидов и накопления газгидратов описывается нелинейной системой из 8 уравнений в частных производных, а именно:
Движение порового флюида к поверхности описывается уравнением Дарси
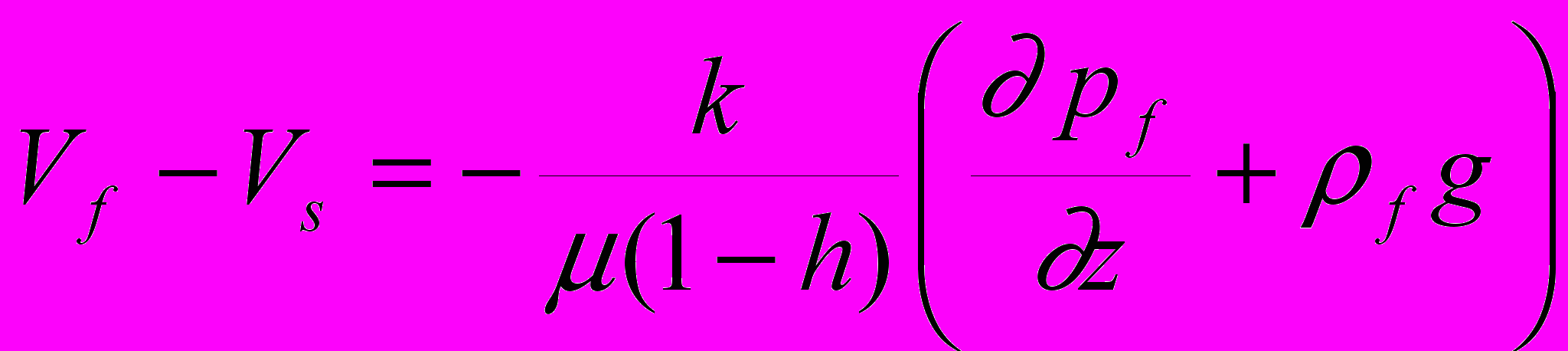 (6.1)
(6.1) h –гидратонасыщенность пор, остальные параметры описаны ранее в главе 2.
У

равнения баланса масс для порового флюида и насыщенной пористой среды записываются как :
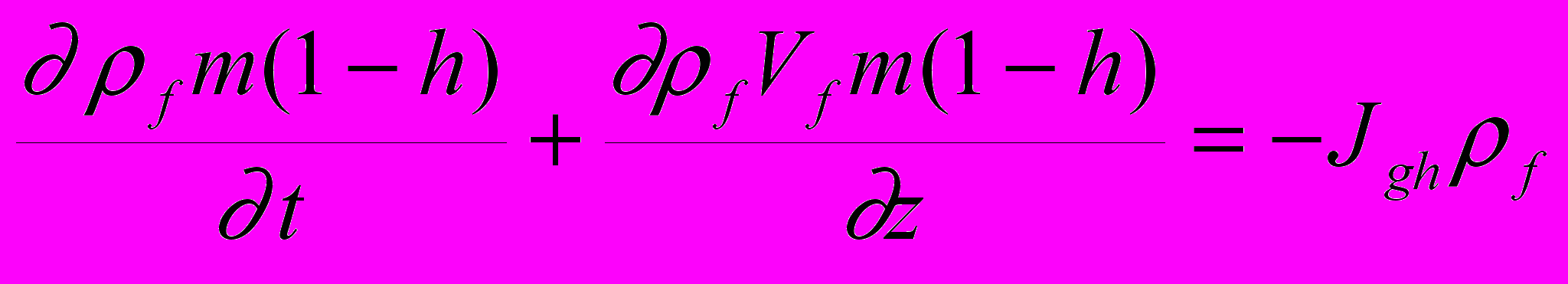 (6.2)
(6.2)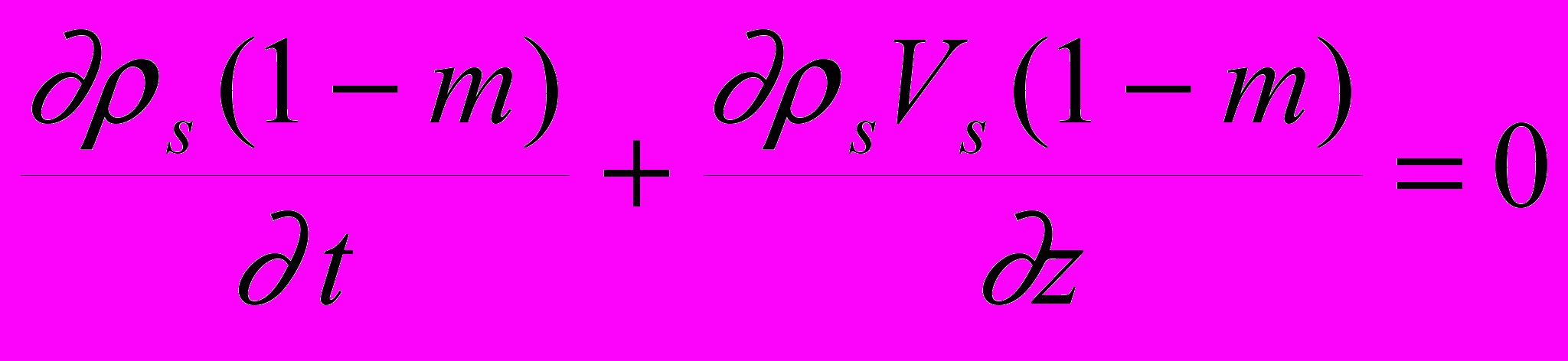 (6.3)
(6.3)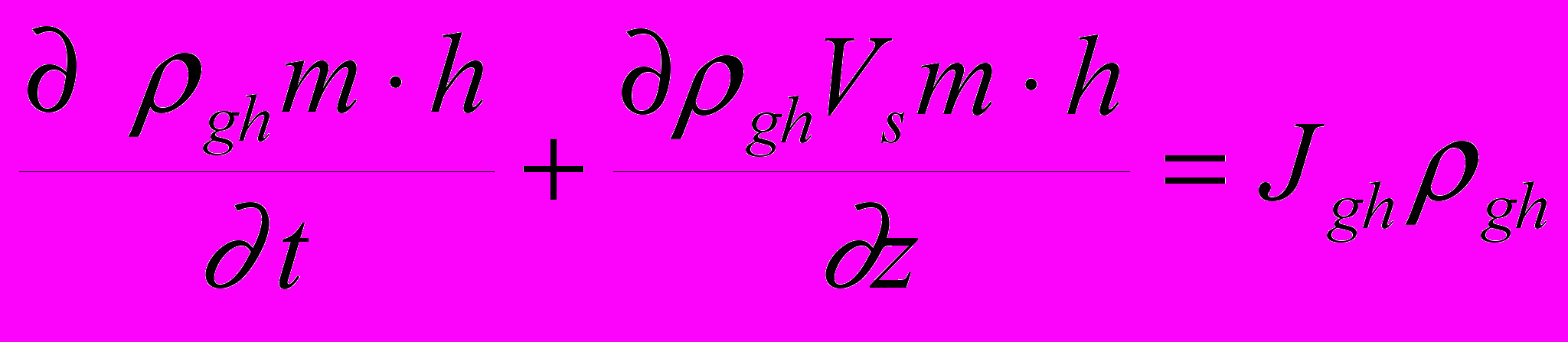 (6.4)
(6.4)где ρs - плотность осадков. Правые части в уравнениях (6.2 )и (6.4) (объемная скорость поглощения флюида и приращения образования гидрата), в предположении локального термодинамического равновесия и отсутствия дефицита газа, используются следуя работе [Davie, Buffet, 2001].
При росте газгидратов происходит поглощение содержащегося в поровом флюиде газа. Модификация уравнения сохранения для растворенного газа в предположении отсутствия дефицита газа [Rempel, Buffet, 1998] для случая непостоянного потока флюида [Суетнова 2007] дает:

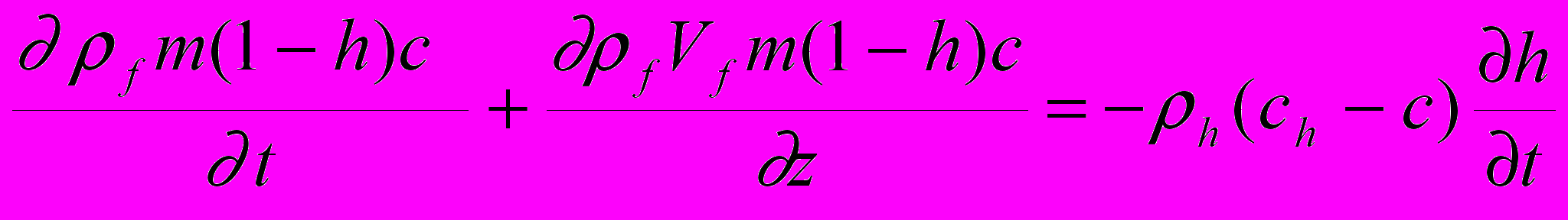 ( 6.5)
( 6.5)c- концентрация метана в флюиде
ch –концентрация метана в гидрате
Для вычисления концентраций газа задается зависимость ceq ( равновесная концентрация метана в поровом флюиде) от давления и температуры в области стабильности газгидратов,
ceq(T)= ceq(T3(P))exp((T-T3(P))/τ) для T
, где τ~14.4oC,
а T3(P), положение фазовой границы стабильности [Davie, Zatsepina, Buffet, 2004]. Процесс уплотнения насыщенной среды осадков, подчиняющийся реологическому закону Максвелла, модифицированному с учетом принципа эффективного напряжения Био-Терцаги для пористой среды записывается как (глава 2 ) :
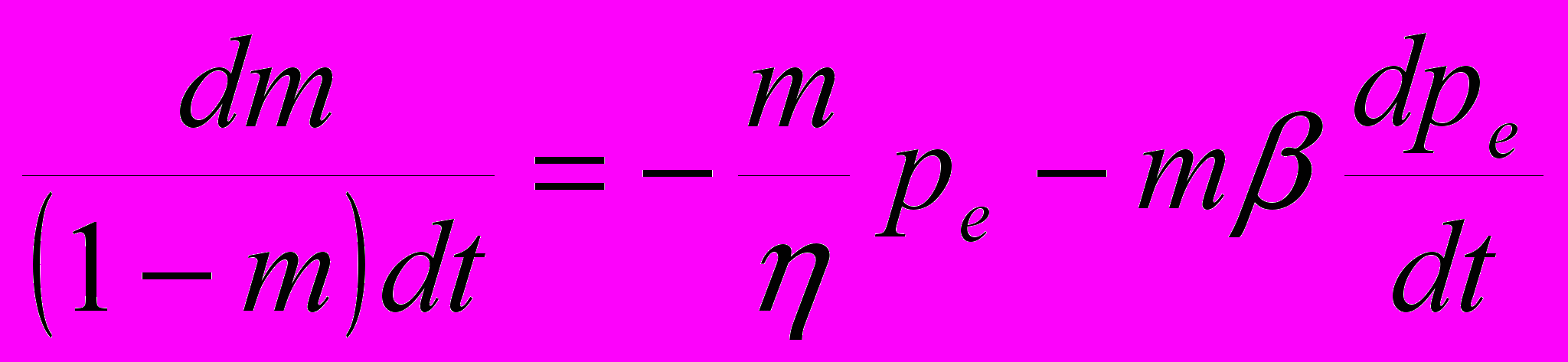 (6.7)
(6.7)Уравнение теплопроводности записывается как
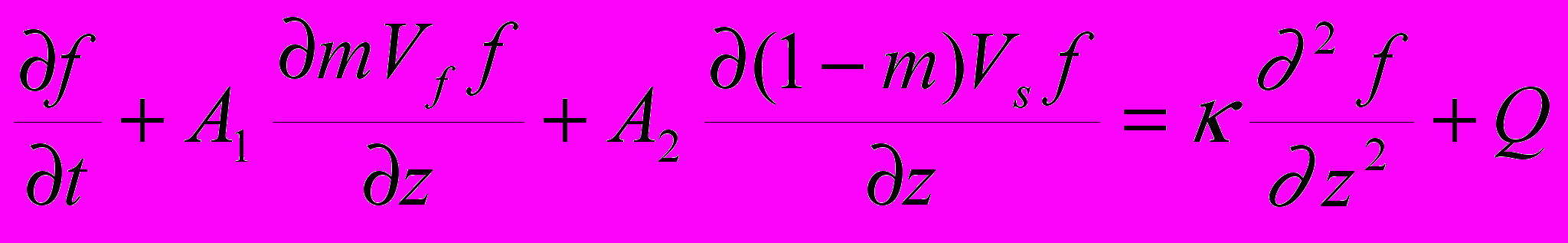 (6.8)
(6.8)f –температура; κ-температуропроводность осадков, Q- теплота фазового перехода.
A1 =
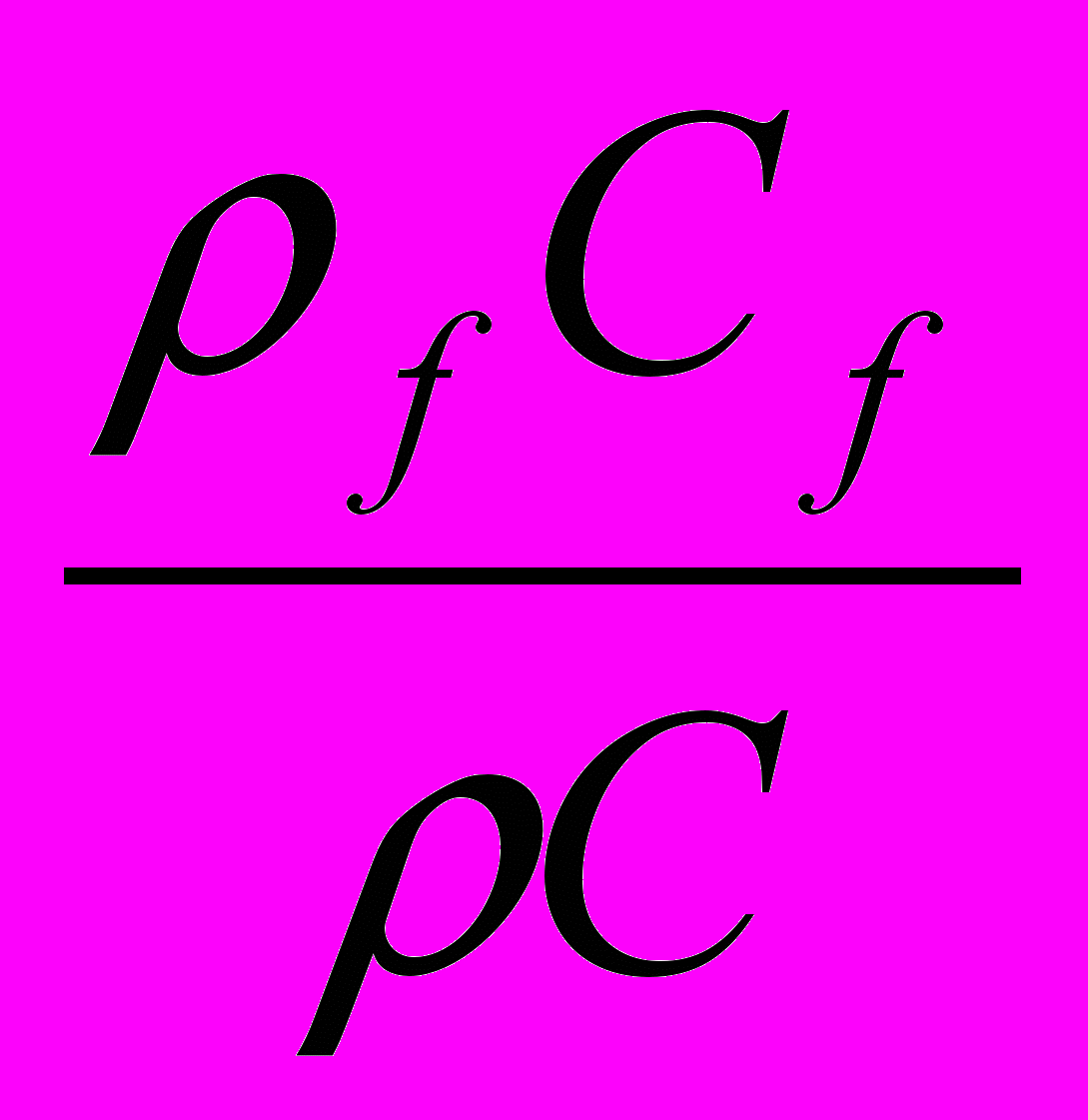 ; A2 =
; A2 =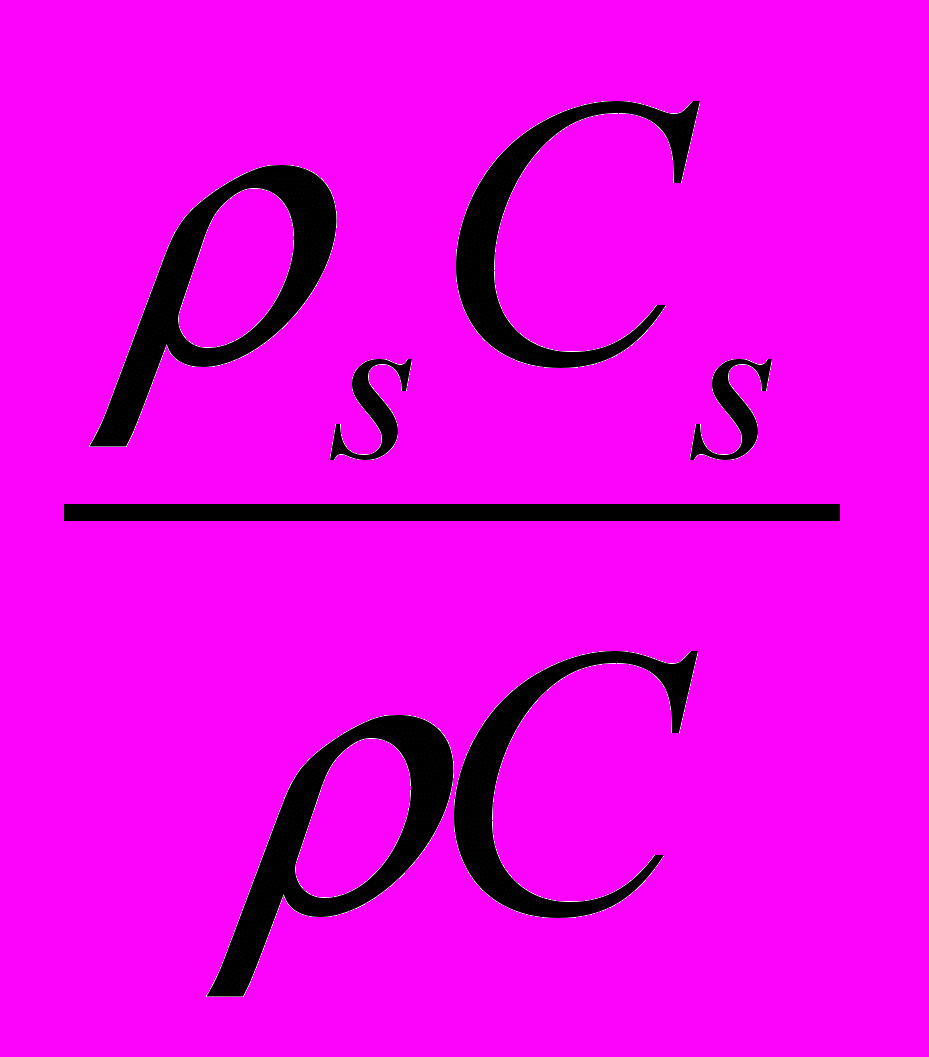
Система (6.1-6.8) становится полной и замкнутой после формулировки граничных условий сформулированных в главе 2 : на нижней, непроницаемой границе осадков z =b(t), скорости твердой V

s и жидкой Vf фаз обе равны V1, - скорости погружения основания бассейна. На верхней дренажной границе, пористость принимается постоянной, m(z=0),t) = mb . Температура на верхней границе области поддерживается постоянной и равной нулю; на нижней границе задается постоянный градиент температуры. Для локализации зоны стабильности гидратов, также должно быть задано давление на поверхности бассейна, отражающее его глубину [Davie, Zatsepina, Buffet, 2004]. Следуя результатам исследований работ [Davie, Buffet, 2001; Xu , Ruppel, 1999] и результатам главы 4, принимается, что температура в осадках растет линейно с глубиной и скрытая теплота реакции гидратообразования не вносит значимых возмущений в профиль температуры. Для газгидрата ставится естественное условие равенства 0 содержания гидрата в порах вне границ зоны стабильности. Сформулированная система была приведена к безразмерному виду, как описано в главе 2, и решалась численно по разработанной программе с использованием литературных данных о возможных значениях входящих физических параметров.
На модельных примерах, рассчитанных с использованием репрезентативных физических параметров системы, показано, как скорость гидратообразования зависит от скорости накопления осадков, и их проницаемости, вязкости и теплового режима осадконакопления. Выявлено, что скорость и объем накопления гидратов из растворенного в флюиде газа, при одинаковом градиенте температуры в осадках и внешнем давлении, определяются значениями безразмерных величин скорости и времени заполнения бассейна, которые являются безразмерными нелинейными комбинациями физических и динамических параметров исследуемого процесса. Расчеты показывают, что чем больше значение безразмерного времени процесса t' при той же безразмерной скорости, тем больше результирующая гидратонасыщенность, а чем больше значение безразмерного комплекса V' «скорость наращивания мощности осадков», тем больше скорость гидратонакопления (рис 6.1, 6.2).
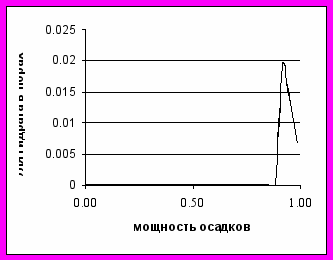
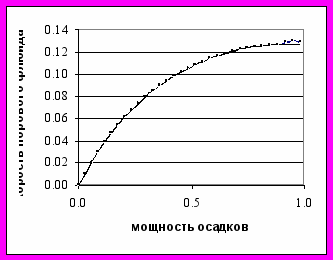
Рис. 6.1. Результаты вычислений для V'= 0.5 10-1 ; t'=0.24 10 (V1=10-10 м/с и конечной мощности осадков 6 км) гидратонасыщенности пор и скорости порового флюида представленные в безразмерном виде. Сплошная кривая скорости -в отсутствии гидратов, маркированная-в случае гидратонакопления.

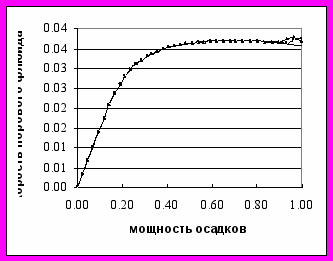
Рис. 6.2. Результаты вычислений для V'=0.5 10-2 ; t'= 0.2 102 ( V1=10-11 м/с и конечной мощности осадков 6 км), гидратонасыщенности пор и скорости порового флюида представленные в безразмерном виде. Сплошная кривая скорости -в отсутствии гидратов, , маркированные-в случае гидратонакопления с различной мощностью зоны стабильности гидрата.
Влияние накопления гидратов на скорость порового флюида отмечается во всех случаях, что отражает взаимовлияние этих процессов за счет изменения свободной пористости. На рис.6.3. приведены результаты сравнения расчетов результирующей гидратонасыщенности для различных значений критериев подобия V и D при одинаковых размерных скоростях осадконакопления и финальной мощности осадков.

Рисунок 6.3. Распределение гидратонасыщенности по глубине для скорости осадконакопления 10-10 м/с. и различных значениях физических и гидродинамических свойств осадков. Ряд1- V = 0.06 D = 0.6 Ряд2- V = 0.06 D = 0.06 Ряд3- V = 0.6 D = 0.6 Ряд4- V = 0.6 D = 0.06
На рисунке 6.3 ясно видно, что при больших значениях параметра подобия V скорость аккумуляции гидратов выше для больших значений параметра подобия D Видно, что для V =0.6 при увеличении значения D в десять раз, с 0.06 до 0.6 (ряд3), финальная гидратонасыщенность увеличилась почти в 1.6 раза по сравнению с результатом для D =0.06 (ряд4), при одинаковом реальном времени процесса. При меньших значениях параметра подобия V влияние величины параметра подобия D на скорость накопления гидратов несущественно. Скорость аккумуляции гидратов оказывается выше при больших значениях V, но при этом безразмерное время оказывается на порядок меньше, что и определяет результирующую гидратонасыщенность при исследованном наборе репрезентативных значений физических и гидродинамических свойств осадков. Таким образом, результаты вычислений и их анализа показывают, как результирующая гидратонасыщенность в процессе накопления и уплотнения осадков и формирования газгидратов в зоне их стабильности зависит и от скорости заполнения бассейна, и от физических и гидродинамических свойств осадков. Гидратонакопление определяется значениями безразмерных критериев подобия задачи уплотнения накапливающихся осадков, являющихся нелинейными комбинациями физических и гидродинамических параметров задачи. Все отмеченные зависимости носят нелинейный характер в силу существенной нелинейности задачи.
Обнаруженная зависимость гидратонасыщенности и скорости ее роста от параметров подобия задачи уплотнения позволяет простым образом сравнивать потенциальную гидратонасыщенность для геофизических объектов, характеризующихся различными физическими параметрами осадков и скоростями их накопления.
Заключение.
В заключении обобщаются выводы, и приводится список публикаций по теме работы.
Выводы
- Модель вязкоупругого процесса уплотнения флюидонасыщенной пористой среды при росте ее мощности представляет механизм, объясняющий характер эволюции пористости и порового давления в течении процесса формирования осадочных толщ.
- Модель дает теоретическое обоснование зависимости характера процесса уплотнения насыщенной пористой среды от физических и гидродинамических свойств среды и скорости наращивания ее мощности.
- Модель позволяет построение серий аналитических и численных решений нестационарных задач, описывающих процесс эволюции тепломассопереноса в двухкомпонентных растущих средах литосферы для выявления основных характеристических свойств поведения решений и возникающих возможных особенностей процессов термомеханической эволюции и условий тепломассопереноса в земной коре на масштабах геологического времени.
На основании анализа результатов модельных расчетов сформулированы закономерности эволюции распределения пористости и эффективного и порового давления по глубине в процессе уплотнения накапливающихся осадков в зависимости от величин параметра подобия ˝время˝ и флюидодинамического и реологического критериев, представляющих собой: 1) отношение скорости роста мощности осадков к гидродинамическому масштабу скорости, характеризующему процесс фильтрации; и 2) отношение времени релаксации Максвелла к масштабу времени процесса уплотнения.
- Полученное методом построения равномерно пригодного асимптотического разложения по малому параметру аналитическое решение задачи уплотнения растущей насыщенной среды позволяет аналитически оценивать характер эволюции пористости и порового давления во времени, и прогнозировать возможное формирование аномально повышенного порового давления, в зависимости от значения выявленного безразмерного критерия подобия, зависящего от физических свойств осадков и скорости их аккумуляции.
- Модель позволяет количественно исследовать возможное влияние накопления в течении роста осадочного слоя осадков с различными физическими и гидродинамическими свойствами на процесс уплотнения и фильтрации флюидов к поверхности и образование гидродинамических барьеров, ловушек (зон относительно повышенной пористости и относительно пониженного давления флюида) и локальных неоднородностей давления флюида.
- Проведенное исследование показывает, как осаждение примесей из насыщающего флюида (на примере образования газгидратов) в зависимости от Р-Т-t условий, будучи зависимым от скорости фильтрации, обусловленной уплотнением, само оказывает влияние на фильтрацию.
- На основании численного моделирования обоснованы количественные закономерности взаимовлияния образования газгидратов из растворенного газа в зоне Р-Т условий стабильности гидратов и процессов фильтрации насыщающего флюида и уплотнения среды.
Список основных публикаций по теме работы
1. E.I.Suetnova. Thermal field near the axial zone of mid-oceanic ridges and heat balance of oceanic lithosphere // Tectonophysics. 1989. V. 159. P. 319-324.
2. Е.И.Суетнова. Тепловой режим осадочных бассейнов в условиях переменного глубинного теплового потока // Доклады АН СССР. 1989. Т. 309, N 1, C с. 65-69.
3. Е.И.Суетнова. Цикличность тепловых процессов в осевых зонах срединно- океанических хребтов и тепловой режим спрединга // Доклады АН СССР. 1991. Т. 320. N 3. C. 600-605.
4. Е.И.Суетнова. Региональные вариации скоростей опускания океанической литосферы и тепловой режим спрединга // Известия РАН. Физика Земли. 1993. N.12. C. 3-8.
5. Глико А.О., Левшенко В.Т., Парфенюк О.И., Петрунин А.Г., Суетнова Е.И. Тепловая эволюция литосферы и условия тепломассопереноса в земной коре // Институт Планетарной геофизики (Основные результаты работы в 1992-1993 гг.). М. 1994. C. 99 – 122.
6. Suetnova E.I., Carbonel R, Smithson S.B. Bright seismic reflections and fluid movement by porous flow in the lower crust // Earth Planet. Sci. Letters. 1994. 126. P. 161-169.
7. E.I.Suetnova, R.Carbonel, S.B.Smithson. Possible pore fluid pressure variations in the lower crust as an explanation of bright seismic reflections in the 1886 PASSCAL Nevada experiment // EOS Trans. 1994. V. 75 S. N 44. P. 486.
8. R. Carbonel, S.B.Smithson, E.I.Suetnova. The extended crust of Western Nevada (Basin and Range Province). // EOS Trans.1994. V .75 S, N 44, P. 678.
9. Е.И.Суетнова, В.М.Чернявский. Об устойчивости неоднородного ползущего течения с деформируемой границей // Докл. РАН. 1997. Т. 354. № 6. С. 762-766.
10. Suetnova E I Balling N. Fluid pressure and seismic reflectivity in the lower crust // Newsletter. 1998. (66) European Geophysical Society. XXIII General Assembly.
