Geum.ru

Шмидта Российской Академии Наук (ифз ран) по адресу; Москва 123995, ул. Большая Грузинская, д. 10. Сдиссертацией можно ознакомиться в библиотеке Учреждения ран институте физики Земли им. О. Ю. Шмидта ран автореферат

Вид материалаАвтореферат
Подобный материал:
1   2   3   4   5
Глава 1. Моделирование процессов тепломассопереноса в флюидонасыщенных областях земной коры (Обзор).


Первая глава носит обзорный и постановочный характер. Здесь приводится анализ комплексных геологических и геофизических данных о строении и эволюции флюидосодержащих толщ земной коры, рассматриваются как их общие характерные черты, так и особенности строения, полученные на основе данных геофизических исследований. Значительные регионы земной коры фактически являются выраженной мультикомпонентной средой, содержащей переменное количество флюида (обычно жидкость) рассеянного в трещинах, порах или межзеренном пространстве твердой породы (Файф, Прайс, Томсон, 1981). Примерами таких регионов являются рифтовые зоны и зоны интенсивного осадконакопления, такие как осадочные бассейны, континентальные окраины, глубоководные желоба, в которых поровый флюид участвует в процессах формирования структуры коры и определяет специфику процессов тепломассопереноса в этих зонах. При наращивании мощности осадочного чехла Земли происходит ряд геофизических и геохимических процессов, формирующих структуру осадочных пород, и базовым процессом является уплотнение и связанная с ним фильтрация к поверхности насыщающего флюида. Исследование динамики уплотнения осадков при их накоплении и погружении является важным элементом решений как фундаментальных задач формирования и эволюции осадочных областей земной коры, так и прикладных задач миграции поровых флюидов и формирования пористых коллекторов в осадочных бассейнах. Результаты геофизических исследований структуры земной коры осадочных регионов дают основание заключить, что процессы миграции к поверхности свободного флюида и уплотнение осадков происходили по однотипному механизму. Процессы уплотнения приводят к падению свободной пористости с ростом глубины от поверхности пород вплоть до средней и нижней коры, и прогрессивному обезвоживанию земной коры в течение истории роста мощности осадочного слоя [Hall, 1993]. Однако, при принципиальном сходстве трендов, наблюденные зависимости распределения пористости и порового давления от глубины оказывались различными для различных регионов (рис 1.1) [Hall, 1993]. В первых работах на эту тему, относящихся к тридцатым годам прошлого века были предложены полуэмпирические законы экспотенциального падения пористости с ростом глубины, причем коэффициенты подбирались путем сопоставления с экспериментальными данными по измерениям пористости в скважинах в конкретном регионе и считалось, что распределение пористости по глубине зависит только от типа осадков [Athy, 1930]. Позднейшие модификации закона Ати уже связывали пористость с эффективным давлением, как это было до этого сформулировано в механике грунтов для гидростатического порового давления [Terzaghi, 1923].

.

.

.

.

.

.




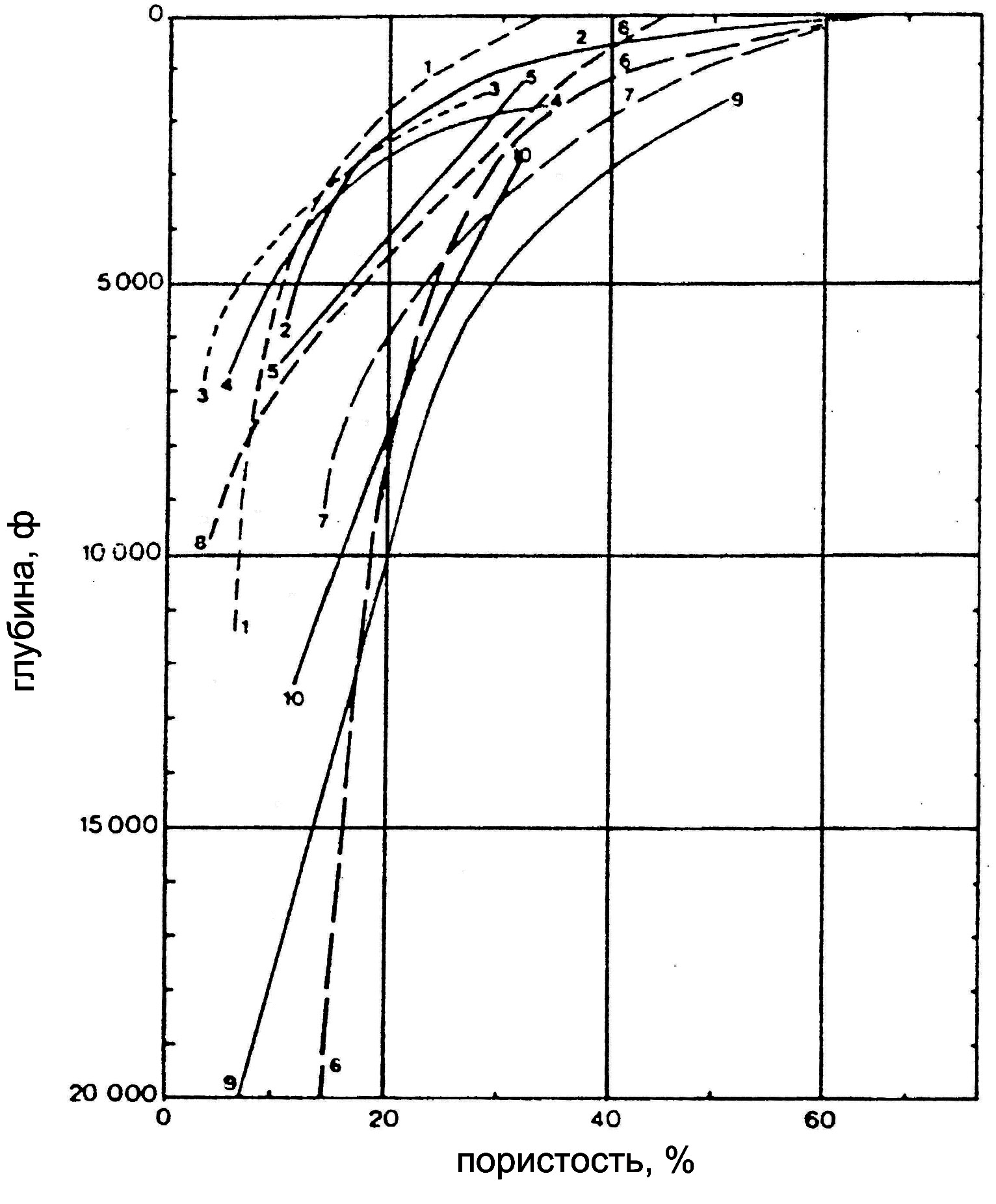
Рисунок 1.1. Распределение пористости по глубине осадочного слоя для различных осадочных бассейнов [Hall P.L., 1993].


В дальнейшем процесс уплотнения осадков исследовался на основе математического моделирования в предположении упругого или упруго-пластического характера деформирования осадков при потере насыщающего флюида [Parasnis , 1960; Magara, 1978; Audet , McConnell , 1992; Wangen, 1997; Luo, Vasseur, Pouya, Lamoureux-Var, Poliakov, 1998]. Такой подход позволял удовлетворительно моделировать распределение пористости в приповерхностных горизонтах, но не давал возможности учесть зависящую от времени, необратимую компоненту уплотнения осадков, наблюдаемую как в природе, так и в лабораторных экспериментах [Bjerrum, 1967; Vasseur, 1998]. Большой объем существенных теоретических результатов, полученных при изучении движения подземных флюидов [Николаевский, Басниев, Горбунов, Зотов, 1970; Файф, Прайс, Томсон, 1981, и др.] касается процессов движения внутрикоровых флюидов и влияния фильтрации на среду коры в масштабах короткого времени и небольших глубин, в предположении упругого деформирования среды, так что процессы, связанные с движением коровых флюидов в геологическом масштабе времени формирования структур коры были разработаны недостаточно.

Зависящая от времени, необратимая компонента уплотнения осадков может численно моделироваться на основании решения задач уплотнения осадков в вязкой постановке, аналогично, например, моделированию фильтрации расплава под рифтовыми зонами [McKenzie, 1984; Каракин, Суетнова, 1989; Stevenson, Scott., 1991] и флюидов в коре [Suetnova, Carbonel, Smithson, 1994]. Были исследованы несколько специальных стационарных и квазистационарных случаев вязкого уплотнения двухкомпонентной флюидонасыщенной среды коры, которые позволили сделать следующий шаг в моделировании геофизического процесса уплотнения осадков [Mckenzie, 1987; Каракин, Суетнова, 1989; Birchwood, Turcott, 1994; Schneider, Potdevin, Wolf and Faille , 1996; Fowler, Yang , 1999; Podladchikov, Connoly, 2000]. Эти исследования, внеся существенный вклад в понимание процессов уплотнения, не давали возможности описать с единых позиций закономерности и особенности эволюции в течении геологической истории основных характеристик процесса уплотнения, таких как распределение пористости, порового давления, скорости флюида и скорости уплотнения осадка для репрезентативной реконструкции динамики процесса уплотнения осадочных толщ в течении времени их формирования.

Однако изучение истории формирования наблюдаемых структур осадков и процессов образования в них полезных ископаемых требует моделирования истории уплотнения и обезвоживания, т.е. динамики фильтрации насыщающего флюида в зависимости от условий осадконакопления, т.к. миграция флюидов к поверхности в земной коре может приводить к скоплению флюидов в аккумулирующих резервуарах и оставлять следы в вмещающей среде в виде рудных проявлений вследствие зависимости от давления параметров растворения и осаждения. Изучение геологической эволюции земной коры и интерпретация данных геофизических измерений требует создания моделей условий тепломассопереноса, учитывающих флюидную компоненту, обусловленную уплотнением, и изучения закономерностей связи процессов движения флюида и уплотнения (деформации) вмещающей породы в течении геологической истории. Этим целям отвечает моделирование с помощью постановки и решения нестационарных задач, учитывающих вязкоупругую реологию среды и описывающих закономерности и особенности эволюции во времени гидродинамических, механических (уплотнение) и тепловых процессов, проходящих в течении формирования флюидонасыщенных регионов земной коры при различных краевых условиях, отражающих специфику процесса накопления осадков. В следующих частях данной работы изложены полученные автором результаты исследований по этому направлению.


Глава 2. Нестационарная задача уплотнения флюидосодержащих осадков вязкоупругой реологии при их накоплении.


2.1 Математическая модель задачи.


Рассматриваемая задача моделирует геологический процесс седиментации и уплотнения накапливающихся осадков при росте осадочной толщи при формировании осадочного бассейна или на континентальной окраине или в глубоководных желобах. Принимается вязкоупругая реология осадков. Течение развивается в области, которая, вследствие осадконакопления, зависит (растет) от времени, и характер этого роста определяется граничными условиями. Течение флюида в пористой деформируемой среде осадков описывается уравнениями неразрывности для флюида и матрицы, уравнением Дарси, определяющим движение флюида относительно матрицы, уравнением движения матрицы, а также динамическим соотношением между давлением флюида и эффективным давлением матрицы.


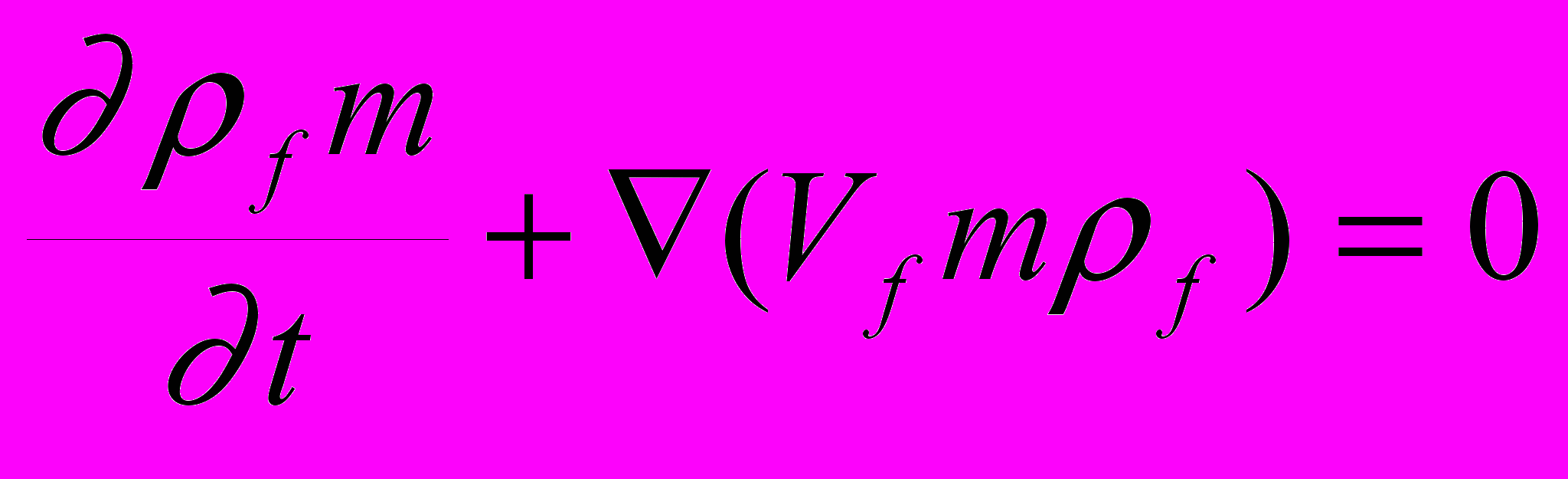(2.1.1)

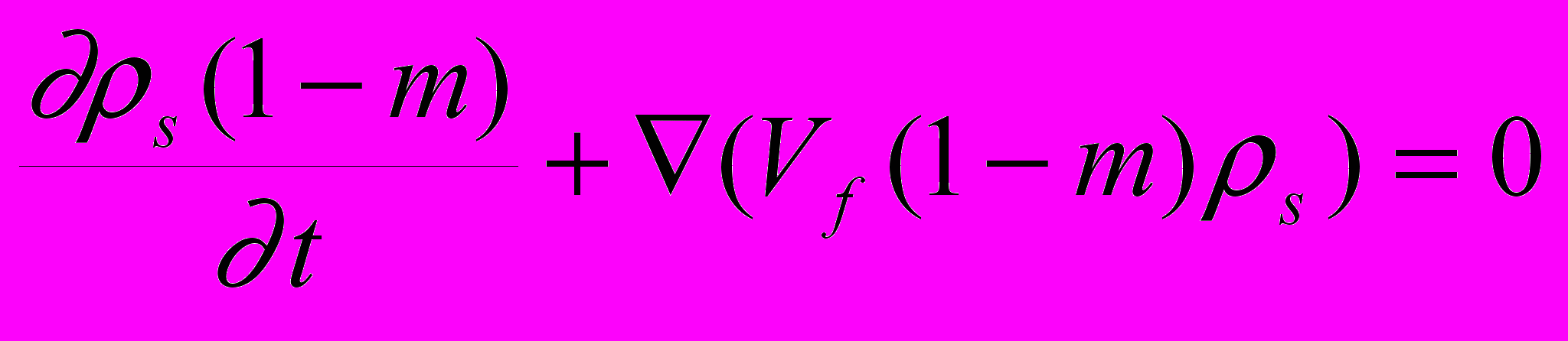(2.1.2)

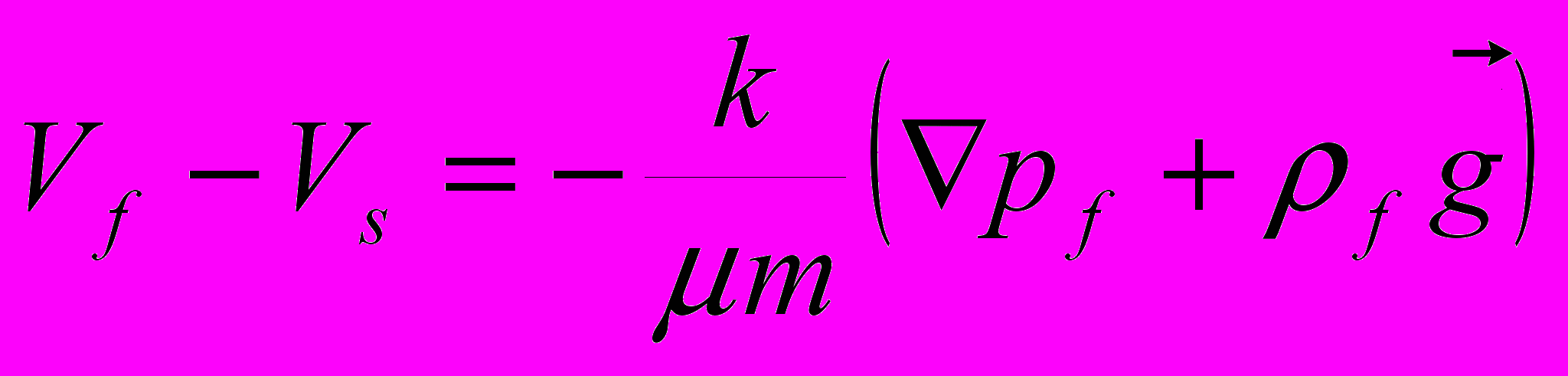(2.1.3)

В рамках модифицированного с учетом принципа эффективного напряжения Био-Терцаги для пористой среды, Максвелловского реологического закона, динамическое соотношение для напряжения и скорости деформации записывается как:


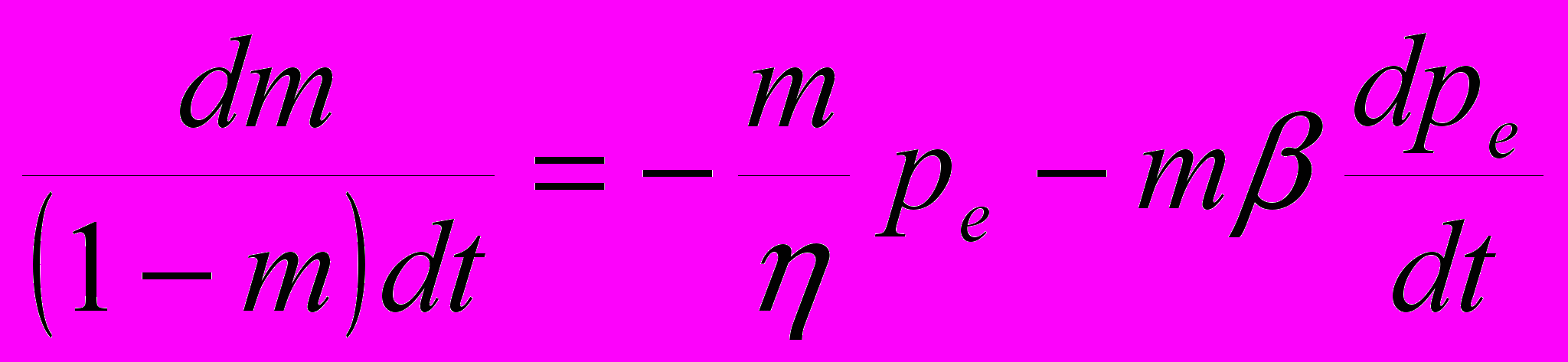(2.1.4.)

Уравнение теплопроводности записывается как

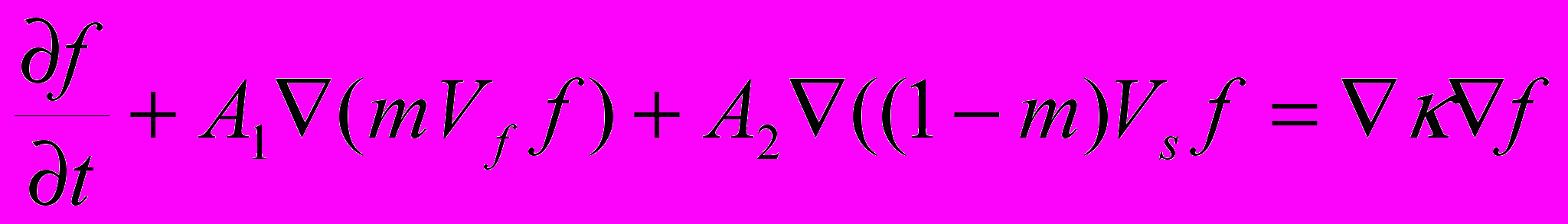(2.1.5)

где А1= 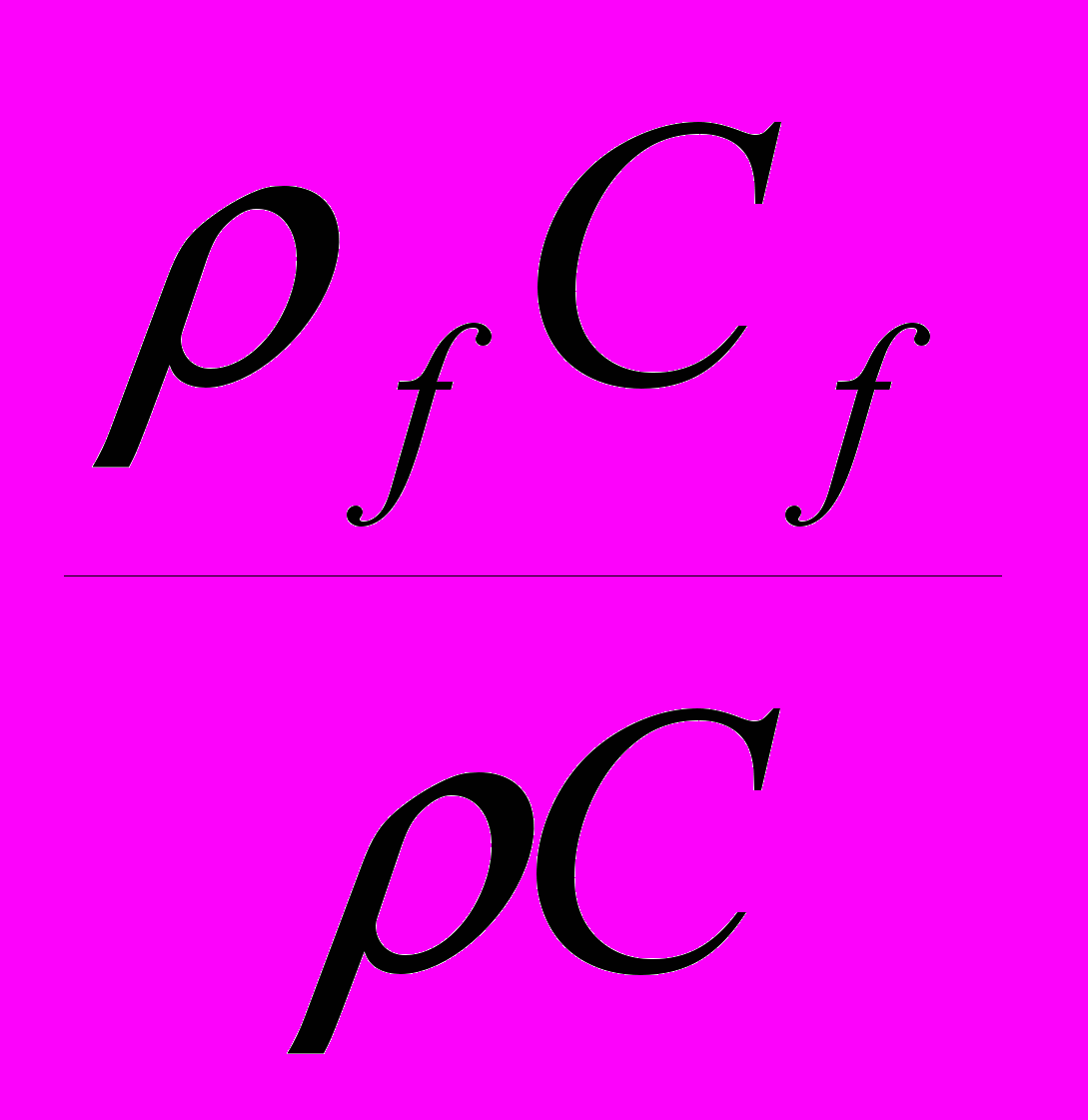, А2= ,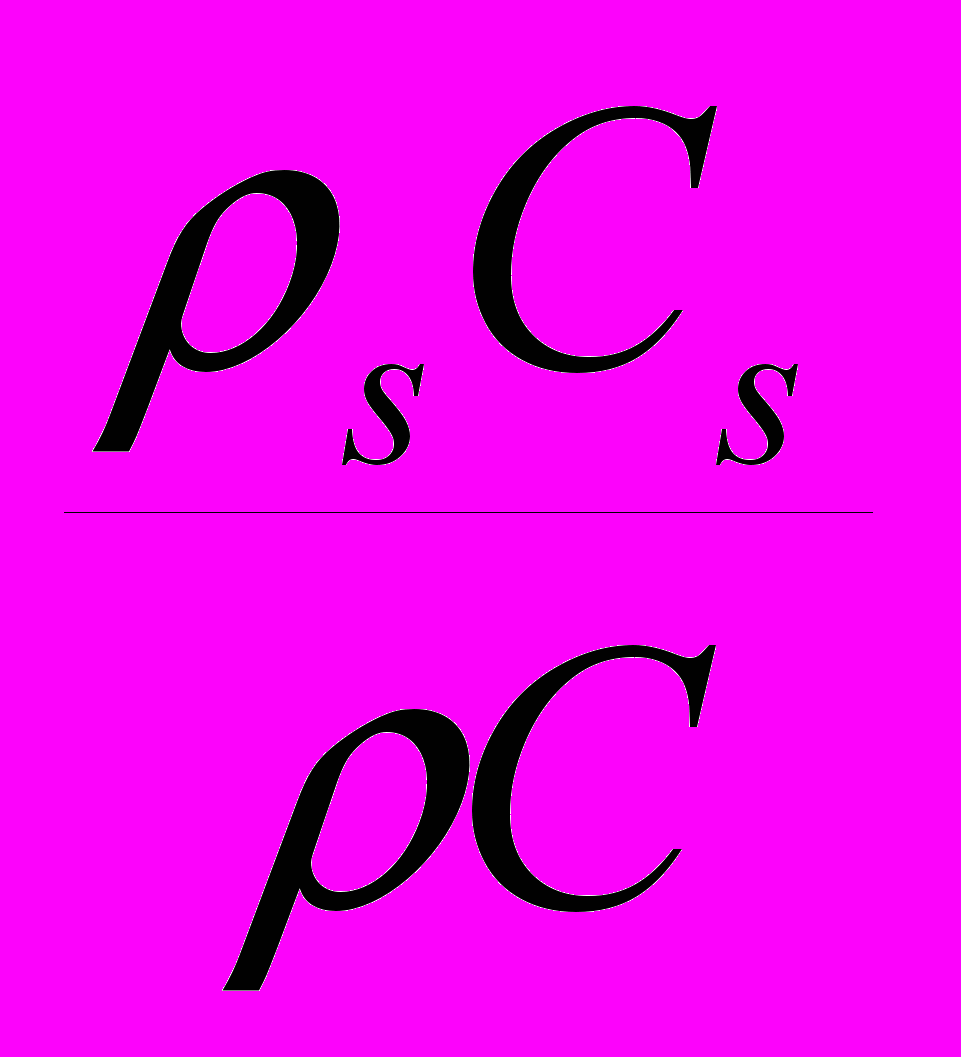

pf -давление флюида,

Vf - скорость порового флюида,

Vs - скорость матрицы осадков, t –время, m-пористость, ρf - плотность флюида, Cf - теплоемкость флюида, ρs - плотность осадков, Cs - теплоемкость матрицы осадков, k - проницаемость, μ - вязкость флюида, g-ускорение силы тяжести, ρ - плотность осадoчной среды, f - температура, κ- температуропроводность осадков, C -теплоемкость осадков, pe -эффективное давление pe = ptot - pf , (ptot-полное авление), η- вязкость осадков [Stevenson , Scott 1991; Birchwood and Turcotte, 1994], β -эффективная сжимаемость среды (в силу предположения вязкоупругой реологии пористой среды β характеризует сжимаемость пор [Gueguen, Palciauskas, 1994]).

В работе далее система уравнений рассматривалась в одномерной постановке, в соответствии с целью - исследовать уплотнение при процессе наращивания мощности слоя за счет поступления на поверхность осадков, который обусловливает миграцию флюида к поверхности под действием гравитационных сил. Горизонтальный размер слоя предполагается много больше вертикального и накопление осадков на поверхность растущего слоя принимается однородным по поверхности. Рассматриваемая задача не включает рассмотрение в уравнении баланса энергии вклада теплогенерации осадков, и зависимости тепловых свойств от PT условий [Bethke, 1985; Миклашевский, Попов, и др., 2006], что, в рамках сформулированной цели исследования не снижает общности результата. Система (2.1.1-2.1.5) становится полной и замкнутой после формулировки следующих граничных условий (без потери общности рассматривается скомпенсированное осадконакопление): на нижней, непроницаемой границе осадков y =b(t), скорости твердой V

s и жидкой Vf фаз обе равны V1, - скорости погружения основания. Пористость на верхней границе, являющейся дренажной, постоянна m(y=0),t) = mb и эффективное давление pe =0. Температура на поверхности осадков поддерживается постоянной и на нижней границе задается градиент температуры


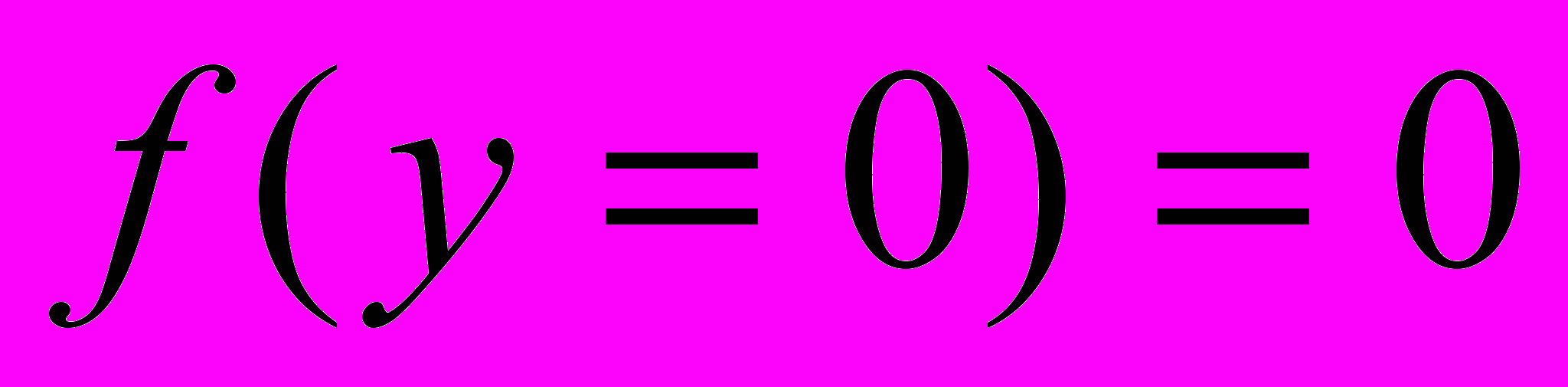
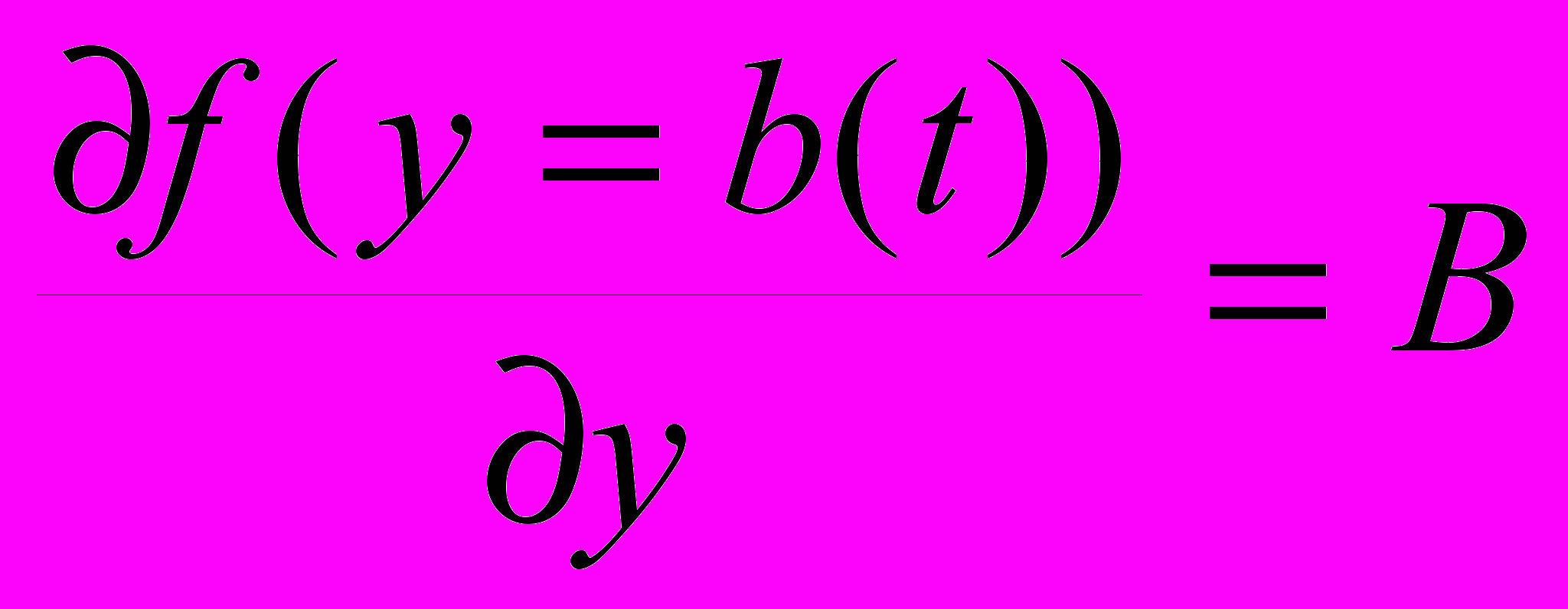
2.2. Физические параметры модели и масштабирование.


Уравнения (2.1.1-2.1.5) включают коэффициенты, которые являются физическими параметрами модели совместно с граничными условиями.

Проницаемость, являющаяся по экспериментальным наблюдениям, нелинейной функцией пористости, обычно в моделях рассматривается как степенная функция пористости [Николаевский, Басниев, Горбунов, Зотов, 1970 ] и показатели степени варьируют от 2 или 3 [Birchwood, Turcott, 1994] до 8 [Fowler, Yang, 1999]. В работах, сделанных в рамках “Basin modeling” [Bethke, 1985], принимают логарифмическую зависимость проницаемости от пористости, и вопрос вида зависимости проницаемость-пористость продолжает быть предметом исследований. В данной работе принимается зависимость проницаемости от пористости k=k0 ml , l=2; 3. Величина k0 зависит от типа осадков. Экспериментальные значения проницаемости для осадков могут варьировать от 10-12 до 10-21м2 [Файф, Прайс, Томсон, 1981; Gueguen and Palciauskas, 1994]. Используя данные имеющиеся в литературе в данной работе был принят для k0 диапазон от 10-15 до 10-17 м2. Следующий модельный параметр - вязкость осадочной среды, принимается не зависящей от температуры и давления на масштабах исследуемых глубин и варьируется в диапазоне 1019 Па с -1022 Па с [Birchwood, Turcott 1994; Schneider, Potdevin, Wolf, Faille, 1996]. Параметр  оценивается как 10-10 Па-1 - 10-9 Па -1 [Hart and Wang, 1995; Berryman, 1992]. Скорость погружения основания осадков (при скомпенсированном осадконакоплении она определяет скорость роста мощности слоя) V которая, в общем случае, непостоянна в ходе формирования бассейна, согласно литературным данным оценивается как 10-10мс-1-10-11мс-1, что согласно литературным данным является типичными величинами [Audet, 1996; Fowler, Yang,1999]. Остальные принятые физические параметры модели соответственно равны :ρ=2.6 10--4 Па с, ρf=1.0103 кг м-3, ρs=2.65103 кг м-3.

Используя приведенные выше величины входящих параметров и следуя классической теории вязкоупругости [Nadai, 1963], мы можем оценить время Максвелловской вязкоупругой релаксации , как 109 с - 1012 с , и следовательно, можно ожидать заметного проявления вязких эффектов уплотнения накапливающихся осадков на временах порядка от сотен до тысяч лет в зависимости от свойств осадочной среды. Предполагая, что механические параметры задачи не зависят от температуры, мы можем исследовать механику и гидродинамику уплотнения. Для построения и исследования решений был произведен переход в систему координат, движущуюся со скоростью погружения основания осадков, и произведена замена переменных и необходимая процедура масштабирования и приведения к безразмерному виду переменных и коэффициентов для выявления параметров подобия [Баренблат, 1982; Седов, 1977] так что, масштабом длины является 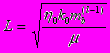; масштабом времени является 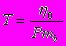. Масштабом пористости является mb и масштабы давления и скорости, записываются как P=∆ρgL, V=L/T.

В безразмерных переменных и после перехода в движущуюся систему координат задача записывается как

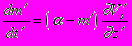(2.2.1)

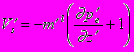(2.2.2)

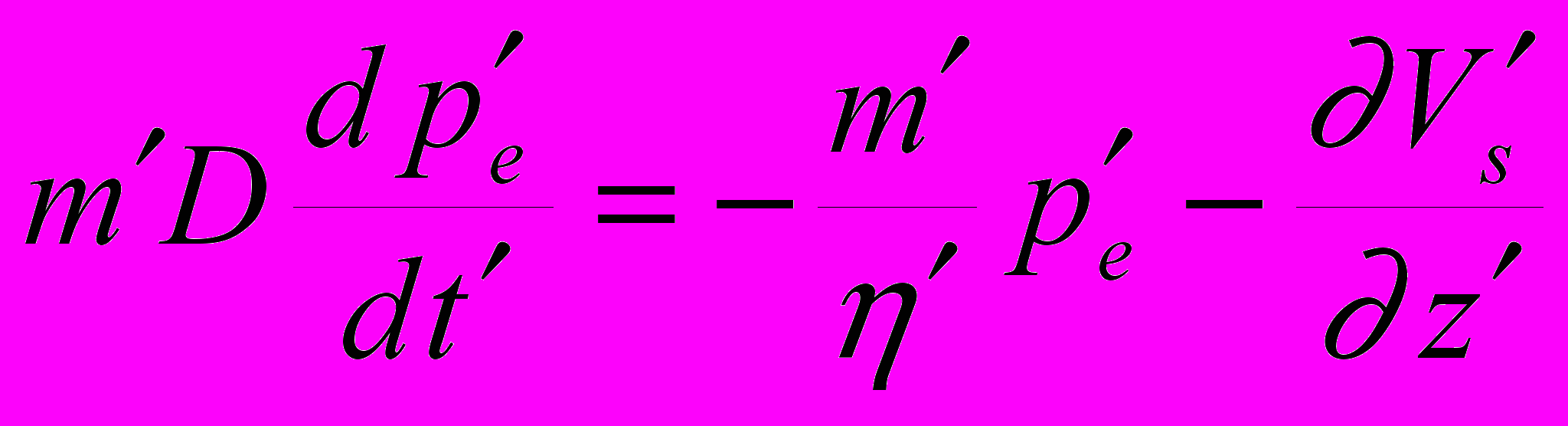(2.2.3)

m, Vs и pe - безразмерные неизвестные и a = 1 / mb .


В системе уравнений (2.2.1-2.2.3) все коэффициенты и переменные представляют из себя безразмерные величины: z=z/L, t=t/T, pe=pe/P,. Vs= Vs /(L/T), a = 1 / mb , η=η/ηo, D= βp=βp Pmb= η0 βp/T. Граничные условия записываются как:Vs(z=0,t)=0 ; p (z=h( t),t)=0; m(z=h(t),t)=1; m(z,t=0)=minitial(z). Скорость движения верхней границы области V0= V0 /(L/T). Безразмерные параметры V0 = V и D являются нетривиальными критериями подобия сформулированной системы уравнений.


2.3. Численное решение


Для решения полученной нелинейной системы уравнений в частных производных в области с движущейся границей была написана программа для персонального компьютера (приводится в приложении). Система уравнений (2.2.1-2.2.3) решалась численно модифицированным методом конечных разностей. Алгоритм решения задачи в наращиваемой области был построен по полунеявной схеме с контролем переменного шага по времени [Флетчер, 1991; Press et al, 1992 ], обновлением сетки в соответствии с ее уплотнением на каждом шаге по времени, и наращиванием элементов сетки в соответствии с дискретной аппроксимацией скорости роста области и контролем устойчивости [Флетчер, 1991; Press et al, 1992].

На рисунках 2.1 (а,b) показаны результаты расчетов для следующих значений физических параметров задачи: V0= 10-11 м с-1, ηo =51020 Па с, β =10-9 Па -1, k0 =10-15м, и конечная толщина бассейна принималась равной 4 км. Такой набор параметров модели приводит к следующим значениям масштабных параметров T и L : T = 71013 с, L =4.3103м и масштабированной скорости роста границы V0 = 0.016.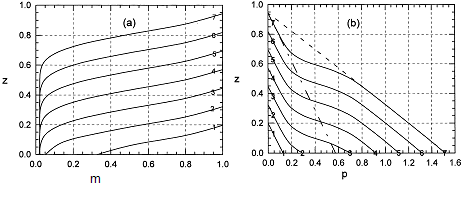





Рисунок 2.1а ,b . Результаты расчетов распределения пористости и порового давления по глубине в различные моменты времени формирования бассейна. Все величины на рисунках безразмерные.


На рисунке 2.2а,б. показаны результаты расчетов для различных моментов времени для следующих значений физических параметров задачи: V0= 10-11 м с-1, ηo =51020 Па с , β =10-9 Па -1 , k0 =10-16м , и конечная мощность осадков принималась равной 4 км. Такой набор параметров модели приводит к следующим значениям масштабных параметров T и L : T = 2.21014 с, L =1.4103м и безразмерной скорости роста границы V0 = 1.6





Рисунок 2.2. а ,b . Результаты расчетов распределения пористости и порового давления по глубине в различные моменты времени формирования бассейна. Все величины на рисунках безразмерные.


Численное решение (рис. 2.1, 2.2) показывает, как процесс уплотнения накапливающихся осадков развивается во времени. В результате в верхнем, приповерхностном слое, пористость монотонно уменьшается, а поровое давление растет по глубине, в формирующемся нижнем слое, примыкающем к основанию осадков пористость практически не меняется, оставаясь равной минимальному значению и градиент порового давления близок к литостатическому. В промежуточной области происходит резкое убывание градиента пористости и возрастание градиента давления. В целом наличие такой переходной зоны по давлению на глубине около 3 км. является типичным (Рис 2.2.3.) но не может быть объяснено в рамках моделей упругого уплотнения [Hubbert, Rubey, 1959; Mello, 1994].





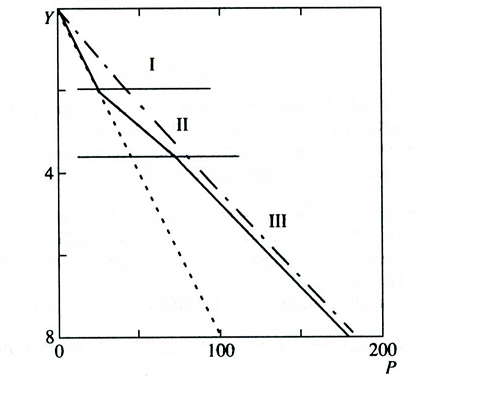
Рисунок 2.2.3. Обобщенное типичное распределение порового давления по глубине осадков в прибрежном бассейне Луизианы [Mello, 1994].


Анализ результатов расчетов позволяет сформулировать следующие закономерности эволюции распределения пористости и порового давления с глубиной в процессе уплотнения накапливающихся осадков.

В любой заданной точке осадков в приповерхностной зоне пористость уменьшается с ростом значения параметра безразмерное время. Так как значение параметра подобия ´безразмерное время´ определяется не только реальным временем процесса, но и физическими свойствами осадков, то осадки меньшей вязкости или (и) большей проницаемости будут демонстрировать большее падение пористости в течение заданного реального времени, чем более вязкие и (или) менее проницаемые. Из анализа результатов численных решений видно, что градиенты падения пористости и роста давления флюида по глубине зависят от значений безразмерного характеристического комплекса V (параметра подобия), являющегося нелинейной комбинацией физических параметров осадков и скорости их аккумуляции. А именно: градиент давления насыщающего флюида в приповерхностном слое оказывается выше при большем значении безразмерного параметра V0 = V. Давление насыщающего флюида повышается с увеличением расстояния от поверхности осадков и градиент развивающегося в накапливающихся и уплотняющихся осадках давления флюида тем больше, чем больше скорость осадконакопления и тем меньше, чем больше пористость и проницаемость поступающих осадков. При формировании осадочной толщи в течении заданного времени, градиент давления флюида будет большим для слоя, на поверхность которого поступали менее проницаемые осадки. Безразмерный параметр подобия D в уравнении (2.2.3) характеризует вклад упругого эффекта в процесс уплотнения. Расчеты показывают, что этот параметр также влияет на распределение порового давления и пористости по глубине [Суетнова, 2008 ], так, что градиент падения пористости по глубине осадков тем больше, чем больше значение механического (реологического) параметра подобия D. Для наглядного выделения роли параметра подобия D на рис 2.2.4. приведены в безразмерном виде результаты расчетов распределения эффективного давления по глубине накапливающихся осадков для одинаковых значений параметра подобия V (V=0.06), и различных значений параметра подобия D (D =0.002-сплошная линия, D =2.- пунктирная линия). Такие значения параметров подобия соответствуют следующим значениям реальных параметров исследуемого процесса: 1) V0= 10-11 м с-1, ηo =11020 Па с , β =10-10 Па -1 , k0 =10-15м , m0=0.3 и финальной мощности осадочного слоя равной 8км; 2) V0= 10-11 м с-1, ηo =11021 Па с , β =10-7 Па -1 , k0 =10-15м 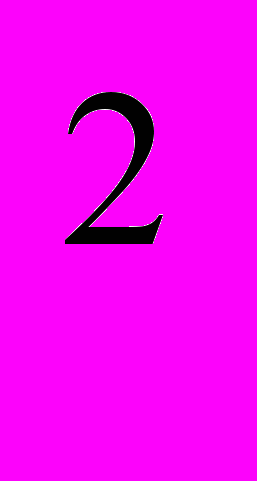, m0=0.3 и той же финальной мощности осадочного слоя равной 8км.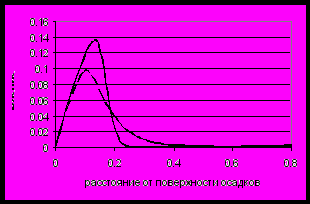




Рис. 2.2.4. Распределение эффективного давления по глубине накапливающихся осадков для одинаковых значений параметра подобия V (V~0.06 ) и различных значений параметра подобия D (D~ 0.002-сплошная линия, D ~2.- пунктирная линия).


Видно, что распределение эффективного давления по глубине зависит от значения параметра подобия D. Чем больше значение D, тем эффективное давление оказывается меньше, и, следовательно, давление насыщающего флюида – больше, для одинаковых значений гидродинамического параметра подобия V и реальной мощности накопленных осадков. Кроме того, глубина перехода давления насыщающего флюида к окололитостатическому давлению (то есть глубина, на которой эффективное давление становится близким к нулю) оказывается большей для большего значения D. Это означает, что число Деборы (De=D/t) оказывается меньше для меньшего значения D и, следовательно, вязкие эффекты в этом случае проявляются больше, что и демонстрирует рисунок 2.4.7. На следующих рисунках 2.2.5а и 2.2.5б представлены графики распределения пористости и порового давления по осадочной колонке для различных значений V и D при одинаковой финальной мощности осадков, которые наглядно показывают различие в градиентах падения пористости и роста порового давления по глубине в зависимости от значений этих критериев подобия.



Рисунок 2.2.5а. Распределение пористости по глубине для скорости осадконакопления 10-10 м/с. и различных значениях физических и гидродинамических свойств осадков. Обозначения: сплошная линия - V = 0.06 D = 0.6, маркировка треугольники- V = 0.06 D = 0.06, квадраты- V = 0.6 D = 0.6, ромбы- V = 0.6 D = 0.06





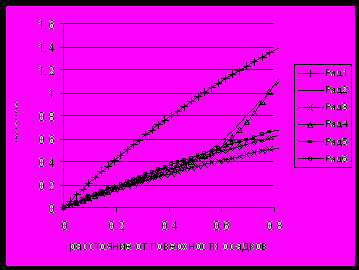
Рисунок 2.2.5б. Распределение порового давления по глубине осадков для скорости осадконакопления 10-10 м/с. и различных значениях физических и гидродинамических свойств осадков. Обозначения: крест-литостатическое давление флюида, косой крест- гидростатическое давление, остальные обозначения как на рисунке 2.2.5а.


Такие значения критериев подобия определяются следующими значениями физических и гидродинамических параметров осадков: V0= 10-10 м/с, η= 5 ·1021 Па· с, k=10-15 м2., β=1/Kp= 10-9 Па -1 , m0 =0.3, V= 0.576, D =0.0649, t=0.766 (обозначение ромбы); V0=10-10 м/с, η=5· 1021 Па· с, k=10-15 м2., β=1/Kp= 10-8 Па -1 , m0 =0.3, V= 0.576, D =0.649 , t=0.78 (обозначение квадраты); V0= 10-10 м/с, η= 5· 1020 Па· с, β=1/Kp= 10-9 Па -1 , k=10-14 м2 , m0 =0.3, V= 0.0576, D =0.0649, t=7.77 (обозначение треугольники); V0= 10-10 м/с, η= 5 ·1020 Па· с , β=1/Kp= 10-8 Па -1 , k=10-14 м2 , m0 =0.3, V= 0.0576 , D =0.649, t=7.80 (обозначена сплошной линией). Из сравнения результатов вычислений следует, что различие в распределении пористости и порового давления в зависимости от значений критерия D проявляется более сильно при большем значении критерия V. Такое различие объясняется тем, что при больших значениях критерия V безразмерное время формирования слоя осадков заданной мощности оказывается меньшим, и, следовательно, большее значение имеют упругие эффекты. Для меньших значений критерия V градиент порового давления в приповерхностном слое оказывается меньшим, и различие в распределении пористости и порового давления в зависимости от значения критерия D оказывается слабее, чем при больших значениях V. Но при меньшем влиянии значения D, при меньших значениях V процесс уплотнения приводит к формированию приповерхностного погранслоя монотонного изменения порового давления и пористости и появлению на определенной глубине осадков резкого возрастания порового давления и резкого убывания градиента пористости. При этом важно отметить, что безразмерное время в этом случае оказывается большим, при том же значении реального времени формирования слоя осадков.

Для построения явной аналитической зависимости эволюции распределения пористости и порового давления в накапливающихся осадках от физических параметров процесса осадконакопления построено асимптотическое решение системы (2.1.1-2.1.5), что позволяет выразить отмеченные зависимости поведения решений в явной форме.