Geum.ru

Уроках математики

Вид материалаУрок

Содержание


Тексты и решение задач
во 2-м классе
Подобный материал:

Нестандартные задачи на уроках математики

К учителю


Известно, что решение текстовых задач представляет большие трудности для учащихся. Известно и то, какой именно этап решения особенно труден. Это самый первый этап – анализ текста задачи. Учащиеся плохо ориентируются в тексте задачи, в ее условиях и требованиях.

Текст задачи – это рассказ о некоторых жизненных фактах:

"Маша пробежала 100 м, а навстречу ей..."

"Ученики 1-го класса купили 12 гвоздик, а ученики 2-го... "

"Мастер сделал за смену 20 деталей, а его ученик..."

В тексте важно все: и действующие лица, и их действия, и числовые характеристики. При работе с математической моделью задачи (числовым выражением или уравнением) часть этих деталей опускается. Но мы именно и учим умению абстрагироваться от некоторых свойств и использовать другие.

Умение ориентироваться в тексте математической задачи – важный результат и важное условие общего развития ученика. И заниматься этим нужно не только на уроках математики, но и на уроках чтения и изобразительного искусства. Некоторые задачи – хорошие темы для рисунков. И любая задача – хорошая тема для пересказа. А если в классе есть уроки театра, то некоторые математические задачи можно инсценировать. Разумеется, все эти приемы: пересказ, рисунок, инсценировка – могут иметь место и на самих уроках математики. Итак, работа над текстами математических задач – важный элемент общего развития ребенка, элемент развивающего обучения.

Но достаточно ли для этого тех задач, которые имеются в ныне действующих учебниках и решение которых входит в обязательный минимум? Нет, недостаточно. В обязательный минимум входит умение решать задачи определенных типов:

о числе элементов некоторого множества;
о движении, его скорости, пути и времени;
о цене и стоимости;
о работе, ее времени, объеме и производительности труда.

Указанные четыре темы являются стандартными. Считается, что умение решать задачи на эти темы может научить решать задачи вообще. К сожалению, это не так. Хорошие ученики, умеющие решить практически любую задачу из учебника на перечисленные темы, часто бывают не в состоянии понять условие задачи на другую тему.

Выход заключается в том, чтобы не ограничиваться какой-либо тематикой текстовых задач, а решать и нестандартные задачи, то есть задачи, тематика которых не является сама по себе объектом изучения. Ведь не ограничиваем мы сюжеты рассказов на уроках чтения! Нестандартные задачи нужно решать в классе ежедневно.

Чтобы облегчить поиск таких задач для решения на уроках в 1-м классе, предлагаю этот материал. Число задач в ней таково, что можно выбрать из них задачи для каждого урока: по одной на урок. Задачи решаются дома. Но очень часто нужно разбирать их и в классе. Среди предлагаемых задач есть такие, которые сильный ученик решает моментально. Тем не менее нужно требовать и от сильных детей достаточной аргументации, объясняя, что на легких задачах человек учится способам рассуждения, которые понадобятся при решении трудных задач. Нужно воспитывать в детях любовь к красоте логичных рассуждений. В крайнем случае можно добиваться от сильных учеников таких рассуждений, требуя построить объяснение, понятное для других – для тех, кто не понимает быстрого решения.

Среди задач есть совершенно однотипные в математическом отношении. Если дети увидят это, – замечательно. Учитель может и сам показывать это. Однако недопустимо говорить: решаем эту задачу, как ту, и ответ будет такой же. Дело в том, что, во-первых, не все учащиеся в 1-м классе способны к таким аналогиям. А, во-вторых, в нестандартных задачах фабула не менее важна, чем математическое содержание. Поэтому лучше подчеркивать связи между задачами со сходной фабулой.

Тексты и решение задач

в 1-м классе

1. Портфель Коли помещается в портфеле Васи, а портфель Васи можно спрятать в портфель Севы. Какой из этих портфелей самый большой?

Эта задача о свойствах предметов. Но о размерах портфелей сообщается опосредованно – через возможность одному из них поместиться в другом. Заметим, что эти свойства не эквивалентны: если один портфель не помещается в другом, то из этого не следует, что он больше. Но если один портфель помещается в другом, то из этого следует, что он меньше. Нужно добиться четкого решения задачи в три этапа:

1) Так как портфель Коли помещается в портфеле Васи, то портфель Коли меньше портфеля Васи.
2) Так как портфель Васи можно спрятать в портфеле Севы, то портфель Васи меньше портфеля Севы.
3) Так как портфель Коли меньше портфеля Васи, а портфель Васи меньше портфеля Севы, то портфель Севы самый большой.

При анализе решения желательно сопроводить этот сюжет рисунком на доске и в тетрадях: изобразить портфели в виде отрезков с буквами к, в и с. С самого начала нужно приучать детей изображать отрезками любые объекты, о которых известно, что один из них больше другого или равен ему.



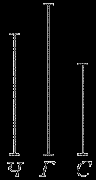
2. Температура тела у человека меньше температуры тела голубя, но больше, чем у слона. У кого из них термометр покажет самую низкую температуру?

И в этой задаче речь идет о свойствах объектов. В данном случае сравнивается температура, а вывод требуется делать о показаниях термометра. Мы вводим ребенка в круг понятий, связанных с измерением температуры: с термометром и со словоупотреблением "температура ниже" – значит меньше. Ход решения и здесь в три этапа:

1) У человека термометр покажет более низкую температуру, чем у голубя, так как температура у человека меньше.
2) У слона термометр покажет более низкую температуру, чем у человека, так как температура у слона меньше.
3) Значит, самую низкую температуру термометр покажет у слона.

При анализе задачи можно нарисовать отрезки – столбики термометра – с надписями Ч, Г и С.



3. Если провести более твердым по менее твердому, то на менее твердом может остаться след, царапина. Останется ли царапина, если провести стеклом по картону? Картоном по стеклу?

Здесь ученик знакомится с еще одним свойством вещей – их твердостью – и со способом сравнения твердости. Нужно получить ответ: стекло оставит царапину на картоне, так как оно тверже; картон не оставит царапины на стекле, так как стекло тверже картона.

4. Если провести стеклом по мрамору, на мраморе окажется царапина. А если провести алмазом по стеклу, царапина останется на стекле. Какой из этих материалов самый твердый?

В этой задаче известны результаты взаимодействия веществ, а вывод требуется сделать об их сравнительной твердости. Решение в три этапа:

1) Стекло тверже мрамора, так как оставляет на нем царапину.
2) Алмаз тверже стекла, так как оставляет на нем царапину.
3) Следовательно, алмаз самый твердый из этих трех веществ.

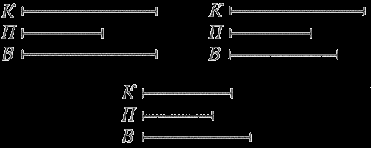
5. Мама дала по яблоку трем своим детям. Катино яблоко тяжелее, чем Петино, а Петино легче, чем Васино. Какое яблоко самое большое, а какое самое маленькое?

Здесь в условии говорится о сравнительной тяжести яблок, а вывод требуется сделать об их сравнительной величине. Детям должно быть понятно, что чем тяжелее яблоко, тем оно больше. Вдобавок, условие о том, что Васино яблоко тяжелее Петиного, дано в косвенной форме. Решение в три этапа:

1) Катино яблоко больше Петиного, так как оно тяжелее его.
2) Васино яблоко тяжелее Петиного, так как Петино яблоко легче Васиного. Значит, Васино яблоко больше Петиного.
3) Неизвестно, какое яблоко самое большое, а какое самое маленькое – известно. Это Петино яблоко. Рисовать отрезки здесь обязательно. Нужно дать все три варианта рисунков: когда Катино и Васино яблоки равны между собой, когда Катино больше Васиного и когда Катино меньше Васиного. При этом во всех случаях нужно изображать Петино яблоко самым маленьким из трех отрезков.


во 2-м классе


1. Сколько весит арбуз?



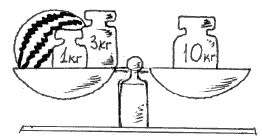
Решение: 10 – (1 + 3) = 6 (кг).

Ответ: 6 кг.

2. Шесть пирожных разделили между братьями и сестрами так, что у братьев их оказалось на два меньше, чем у сестер. Сколько у кого?

Решение. Задача может быть решена угадыванием. Однако желательно дать и решение с вопросами. Этого можно добиться, если нарисовать два отрезка, один из которых на две клетки больше другого. Как узнать, сколько клеток должно быть в каждом отрезке? Сумма этих трех отрезков должна равняться 6 клеткам. Значит, сумма двух равных отрезков равна 6 – 2 = 4, а каждый из них 2. Когда учащимся покажется, что это рассуждение ими понято, нужно записать его по вопросам и действиям. Нужно подсказать первый вопрос:

1) Сколько было бы пирожных, если бы у сестер было столько же, сколько у братьев? 6 – 2 = 4.
2) Сколько было пирожных у братьев? 4 : 2 = 2.
3) Сколько было пирожных у сестер? 2 + 2 = 4 (или 6 –2 = 4).

Ответ: у братьев 2, у сестер 4.

3. Ваня живет в 12-этажном доме, на 9 этаже, если считать сверху. На каком этаже живет Ваня?

Решение. Можно нарисовать дом, а можно решить задачу и без рисунка, узнав, сколько этажей дома находится ниже Вани (12 – 9 = 3).

Ответ: На 4 этаже.

4. В коробке лежит 15 шариков: черных, белых и красных. Красных шариков в 7 раз больше, чем белых. Сколько в коробке черных шариков?

Решение. Белых шариков не может быть больше одного, так как если бы их было хотя бы 2, то красных шариков было бы не меньше 14, а шариков всего 15. Значит, белый шарик всего один, а красных в семь раз больше, то есть семь. Черных шариков 15 – (1 + 7) = 7.

5. Пес Тузик на 6 кг тяжелее кота Барсика, а Барсик втрое легче Тузика. Сколько весит Барсик?

Решение можно сопроводить рисунком. 6 : 2 = 3 (кг) – вес Барсика.

Ответ: 3 кг.

6. Расшифруй предложение, в котором каждая буква заменена ее номером в русском алфавите и все слова написаны слитно:

(15)1(14)(17)6(19)(15)(33)(19)(20)(18)(16)(10)(20)(30)

(10)8(10)(20)(30)(17)(16)(14)(16)4(1)6(20).

Ответ: Нам песня строить и жить помогает.

7. Придумай возможное продолжение этой последовательности чисел: 1, 1, 2, 3, 5,…

Решение. 1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5. Одно из правил, по которому может быть составлена эта последовательность, таково: первые два числа – единицы, а каждое число, начиная с третьего, равно сумме двух предыдущих чисел.

Ответ: Возможно такое продолжение: 8, 13, 21, …

в 3-м классе

1. 1 февраля 1999 г. был понедельник. Каким днем недели было 1 марта 1999 г.?

Решение. Задачи на эту тему актуальны в переживаемом нами начале века и тысячелетия, их несколько в этой книжке (№ 1, 21, 41, 61, 81, 101, 121 и 141). Все они решаются подсчетом остатка от деления некоторого числа дней на число дней в неделе – на 7. В данной задаче нужно выяснить: сколько дней прошло с 1 февраля 1999 г. до 1 марта 1999 г. (так как 1999 г. был невисокосным, то в феврале было 28 дней); каким днем является день "понедельник + 28 дней" (так как 28 дней – это ровно 4 недели, то "понедельник + 28 дней" – снова понедельник).

Ответ: 1 марта 1999 г. был понедельник.Полезно составить календарь на февраль 1999 г. Из него станет ясно, что ответ получен правильный.

2. Сколько существует трехзначных чисел, все цифры которых – 1, 2 или 3?

Решение. На первое место можно поставить любую из трех данных цифр. На второе – тоже любую из этих трех цифр. Значит, первые два места могут быть заняты девятью способами: 11_ , 12 _, 13 _, 21 _, 22 _, 23 _,31 _, 32 _, 33 _. В любом из этих случаев третье место можно занять любой из тех же трех цифр. Значит, все число можно записать 27 разными способами, от 111 до 333.
Кратко это решение можно высказать так: первой может быть любая из трех цифр, второй – любая из трех цифр, третьей – любая из трех цифр; значит, всего таких чисел 3 x 3 x 3 = 27.

Ответ: 27 чисел.

3. Петя нашел один гриб, Коля – два, а Паша – три. Мама дала им 18 орехов и велела разделить их по заслугам. Сколько орехов получил каждый?

Решение. Паша собрал ровно половину всех грибов, поэтому ему полагается половина всех орехов – девять. Из остальных девяти орехов Коля должен получить в два раза больше Пети, так как он собрал вдвое больше грибов. Значит, Петя должен получить три ореха, а Коля шесть.

Ответ: Петя – 3, Коля – 6, Паша – 9.

4. Во сколько вопросов можно узнать день рождения человека, если он на каждый вопрос отвечает "да" или "нет" (и всегда правдив)?

Решение. Один из 12 месяцев можно узнать в 4 вопроса (так как 12 > 8 и 12 < 16). Вопросы могут быть такими:
Родились ли вы в первом полугодии?
Родились ли вы в первом квартале полугодия?
Родились ли вы в первом месяце квартала?
(Задается, если на третий вопрос получен Ответ "нет") Родились ли вы во втором месяце квартала?
Число в данном месяце определяется в 5 вопросов (так как в месяце больше 16 дней и не больше 32). Эти вопросы могут быть такими:
Родились ли вы с 1 по 16 число?
Родились ли вы в первые 8 из тех 16 дней, которые определены предыдущим ответом?
Родились ли вы в первые 4 из тех 8 дней, которые определены предыдущим ответом?
Родились ли вы в первые 2 из тех 4 дней, которые определены предыдущим ответом?
Родились ли вы в первый из тех 2 дней, которые определены предыдущим ответом?
Нужно проиграть эти вопросы для разных случаев (подробно об этом говорится в моей книжке "Нестандартные задачи во втором классе").

Ответ: 9 вопросов.

5. Среди трех монет одна фальшивая. Она не отличается от настоящей монеты по виду, но немножко тяжелее настоящей монеты. У нас имеются чашечные весы без гирь. Как одним взвешиванием установить, какая монета фальшивая?

Решение. Сравниваем две монеты взвешиванием; если они уравновесятся, то фальшивая монета – третья, если одна из монет окажется тяжелее, то она – фальшивая.

в 4-м классе

1. Сколько разных нарядных костюмов у Андрея, если у него три пары нарядных брюк, два нарядных пиджака и два нарядных галстука и все эти предметы подходят друг другу?

Решение. К любой паре брюк можно подобрать любой из двух пиджаков и любой из двух галстуков. То есть к любой паре брюк можно подобрать четыре варианта "пиджак + галстук". А так как пар брюк имеется 3, то всего нарядных костюмов 12. Желательно начертить на доске такое дерево возможностей:

А еще лучше сделать такой рисунок.



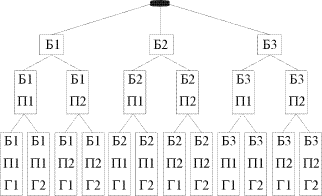
Ответ: 12.

2. Как тремя взвешиваниями на чашечных весах без гирь найти одну фальшивую (более легкую) монету из 20 монет?

Решение. Разделим монеты на три группы: 9, 9 и 2 монеты. Первое взвешивание – сравниваем вес первых двух групп. Если они одинаковы, то фальшивая монета среди двух монет третьей группы, и мы вторым взвешиванием сравниваем их между собой. Та, которая легче, – фальшивая. Если в первом взвешивании одна из групп окажется легче, то фальшивая монета в ней. Делим эту группу на три группы по три монеты. Вторым взвешиванием устанавливаем, которая из этих трех групп легче, а третьим взвешиванием находим легкую монету в этой тройке.

3. Продолжи последовательность: 8, 6, 10, 6, 12, 6, ... .

Решение. Все четные члены последовательности равны 6, а все нечетные получаются прибавлением числа 2 к предыдущему нечетному члену.

Ответ: 8, 6, 10, 6, 12, 6, 14, 6, 16, 6, ... .

4. Разгадай ребус: 5* + **3 = **01.

Решение. Достаточно записать пример в столбик, и решение будет очевидным.

Ответ: 58 + 943 = 1001.

5. В одной бочке 50 л жидкого дегтя, в другой – 50 л жидкого меда. Ложку дегтя переливают в бочку меда, а потом ложку полученной смеси переливают в бочку дегтя. Чего стало больше: меда в дегте или дегтя в меде?

Решение. Это задача на тему поговорки "Ложкой дегтя можно испортить бочку меда". Но интересна она не этим, а тем, что даже взрослые люди часто дают на нее неверный ответ: дегтя в меде больше, так как дегтя перелили целую ложку, а меда перелили не целую ложку (ложку, в которой был также и деготь). После того как будут выслушаны разные ответы, нужно дать такое решение задачи.
В результате переливаний в первой бочке оказалось х миллилитров меда. Так как в ней всего 50000 мл, то дегтя в ней 50000 – х миллилитров. Во второй бочке осталось поэтому 50000 – х миллилитров меда. Значит, дегтя в ней тоже х мл.
И сопроводить решение таким рисунком:



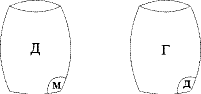
Довод в пользу неверного ответа, который казался таким убедительным, теперь легко опровергнуть: во время второго переливания часть дегтя вернули обратно.

Ответ: поровну.