Управление рисками
| Вид материала | Учебное пособие |
СодержаниеТаблица 11 - Распределение вероятностей для продукта У |
- Концепция магистерской программы «Управление рисками, страхование и актуарные методы», 310.41kb.
- Справка о проведенных занятиях по курсу, 49.56kb.
- «Управление рисками в проектах по созданию программного обеспечения», 103.45kb.
- «управление проектами в сфере бизнеса», 21.93kb.
- Оценка и управление инвестиционными рисками (на примере лизинговой компании), 266.02kb.
- Программа дисциплины Управление рисками в логистике для специальности 061100 «Менеджмент, 223.86kb.
- Пятая Банковская Конференция управление рисками, 287.13kb.
- Рабочая программа по курсу «Управление рисками» для студентов специальности 080502, 23.28kb.
- Управление банковскими рисками, 31.22kb.
- Валтарс Риск Менеджмент Система управления рисками. Принципы построения, внутренние, 43.81kb.
-Точка принятие решений
--Возможные события
Рисунок 16 - Дерево решений
Измерение численного результата (вознаграждения) для каждого возможного исхода в единицах, отражающих степень достижения заданных целей. Чаще всего это выражается в денежном виде, например, прибыль или поток денежных средств, но в некоторых случаях предпочтительнее выражать в других показателях, например, времени, рыночной доле и т.п.
Возможность того, что какое-то событие или внешнее условие наступит, известно под термином вероятность. Как правило, она выражается в виде десятичной дроби, и при этом ее значение находится между 0 и 1, или в процентах. Значение 0 указывает на нулевую возможность тог, что анализируемое событие обязательно случиться. Вероятность, скажем, 0,4 означает, событие, как ожидается, произойдет четыре раза из десяти. Общая сумма вероятностей событий, которые могут произойти, должна составлять 1,0. Например, если педагог говорит, что вероятность того, что студент сдаст экзамен, равно 0,7, то это означает, что у студента шанс на сдачу экзамена равен 70%. Учитывая, что среди других возможных событий, связанных со сдачей экзамена, можно указать только провал на экзамене, то вероятность такого исхода будет равна 0,3.
Информация может быть представлена в виде распределения вероятностей. Это список возможных исходов для анализируемого события и вероятности того, что исход наступить. Распределение вероятности для описанного выше примера имеет следующий вид:
-
Исход
Вероятность
Сдача экзамена
0,7
Провал экзамена
0,3
Итого
1,0
Некоторые вероятности также известны как объективные вероятности, поскольку могут быть вычислены математические или получены на основании исторический достоверных данных. Примерами объективных вероятностей могут быть: подбрасывание монеты или выбрасывание игровой кости. Например, вероятность того, что монета при ее подбрасывании ляжет «орлом» вверх, логически должна составлять 0,5. Это можно проверить на опыте, подбрасывая монету много раз и фиксируя полученные результаты. Аналогично, вероятность поучения цифры 1 при выбрасывании кости равна 0,166(т.е. одна шестая). Это тоже можно объяснить логически и проверить, многократно бросая игральную кость и фиксируя получаемые результаты.
Однако для решений в сфере бизнеса получение объективных вероятностей маловероятно, поскольку в этом случае часто предыдущих данных или повторно проводящихся процессов не бывает. Вероятности здесь приходится оценивать менеджерам на основе собственных суждений. Вероятности, полученные таким способом, называются субъективными вероятностями, поскольку скорее всего в таких условиях даже два человека редко присвоят конкретному исходу одни и те же значения вероятности. Субъективные вероятности оцениваются на индивидуальных знаниях, прошлом опыте и наблюдениях за текущими переменными, которые, возможно, влияют на результат будущих событий. Поэтому маловероятно, что такие вероятности могут быть оценены точно, т.е. любые оценки будущих неопределенных событий связаны с субъективными ошибками.
Преимущество этого подхода в том, что он обеспечивает более обоснованную информацию, которая позволяет указать наиболее вероятный исход. Рассмотрим, например, ситуацию, в которой преподавателя спрашивают о том, сдадут ли экзамен студенты А и В. Преподаватель может ответить, что оба студента, как он ожидает, экзамен сдадут. Это оценка преподавателя с точки зрения наиболее вероятного исхода. Однако более предпочтительно использовать в этом случае распределение вероятностей.
Таблица 3 - Распределение вероятностей
| Исход | Вероятность для студента А | Вероятность для студента В |
| Сдача экзамена | 0,9 | 0,6 |
| Провал экзамена | 0,1 | 0,4 |
| Итого | 1,0 | 1,0 |
Такое распределение вероятностей требует от преподавателя уточнить степень его уверенности в том, каковы будут возможные результаты будущего события. Понятно, что такая информация более значимо, чем простая оценка того, что оба студента, вероятно, сдадут предстоящий экзамен, поскольку показывает, что вероятность того, что студент А экзамен провалит, мала, в то время как для студента В это вполне возможно. Теперь применим принципы теории вероятностей к принятию решений в бизнесе.
Для менеджеров представление распределения вероятностей для каждого альтернативного варианта действий может дать полезную дополнительную информацию, поскольку такое распределение показывает степень неопределенности, которая существует для каждого из этих вариантов. Распределение вероятностей позволяет менеджерам рассматривать не только возможные прибыли (вознаграждения) для каждого альтернативного варианта, но и степень неопределенности этого варианта. Рассмотрим ситуацию, представленную в следующем примере
Таблица 4 - Распределение вероятностей для продукта А
| Исход по прибыли | Оцениваемая вероятность | Взвешенное значение |
| 6000 | 0,1 | 600 |
| 7000 | 0,2 | 1400 |
| 8000 | 0,4 | 3200 |
| 9000 | 0,2 | 1800 |
| 10000 | 0,1 | 1000 |
| | 1,0 | 8000(ожидаемое значение) |
Таблица 5 - Распределение вероятностей для продукта В
| Исход по прибыли | Оцениваемая вероятность | Взвешенное значение |
| 4000 | 0,05 | 200 |
| 6000 | 0,1 | 600 |
| 8000 | 0,4 | 3200 |
| 10000 | 0,25 | 2500 |
| 12000 | 0,2 | 2400 |
| | 1,0 | 8900(ожидаемое значение) |
Менеджер рассматривает целесообразность выпуска продукта А или В, причем одновременно может производиться только один из них. Оцениваемый спрос по каждому продукту неизвестен. Подробное исследование возможного спроса по каждому продукту дает следующее распределение вероятностей прибыли по каждому из них.
Какой продукт компаний выгоднее выпускать?
Из распределения вероятностей, показанных в примере, видно, что существует один шанс из десяти, что прибыль для продукта А составит 6000 д. ед. и четыре шанса из десяти, что она будет д. ед. 8000. Более полезный способ анализа распределения вероятностей связан с тем, что компания по продукту А получит прибыль д. ед.8000 или меньше в семи случаях из 10. Это цифра получается сложением вероятностей для прибыли в д. ед. 6000, д. ед. 7000,и д.ед. 8000. Аналогично можно показать, что у компании вероятность получения прибыли в д. ед. 9000 и больше будет три из десяти.
Ожидаемые значение (иногда его называют ожидаемым вознаграждением) вычисляется взвешиванием каждого уровня прибыли (возможного исхода) в примере 12.2 на соответствующую ему вероятность. Сумма этих взвешенных величин называется ожидаемым значением для распределения вероятностей. Другими словами, ожидаемое значение это взвешенное среднее арифметическое возможных исходов. Для продуктов А и В ожидаемые значение в д. ед.8000 и в д. ед.8900 определяются с учетом не единственного варианта развития событий (единственное наиболее вероятной оценки), а диапазона возможных исходов. Например, единственная наиболее вероятная оценка-это уровень прибыли, который компания получит с наибольшей вероятностью. Для обоих продуктов в рассматриваемом примере наиболее вероятной оценкой является прибыль в д. ед.8000, а от продукта В д. ед.8900 . Ожидаемые значение - это средние результаты возможных исходов, получаемые на основе менеджерских оценок.
Но нет никаких гарантий, что фактические исходы будут равны ожидаемым. Действительно, ожидаемое значение для продукта В распределении вероятностей как таковое не показано.
Помимо ожидаемых значений прибыли для различных альтернативных вариантов менеджеров также интересует степень неопределенности ожидаемых будущих прибылей. Например, предположим, что появилось возможность для еще одного варианта действий, т.е. если вернуться к примеру, то теперь можно выпускать и продукт С. В этом случае распределение вероятностей будет следующим.
Таблица 6 - Распределение вероятностей для продукта C
| Исход | Ожидаемая вероятность | Взвешенное значение |
| Убытки 4000 | 0,5 | -2000 |
| Прибыль 22000 | 0,5 | 11000 |
| | | 9000 (ожидаемое значение) |
Продукт С имеет более высокое ожидаемое значение, чем продукты А и В, но маловероятно, что менеджеры предпочтут продукт С продукту В; слишком высока у него изменчивость возможных исходов. Другими словами, у продукта С более высокая степень неопределенности.
Удобным показателем отклонения распределения вероятностей является стандартное отклонение. Это ()- квадратный корень из среднеквадратического ожидаемого значения, вычисляется по формуле:
=
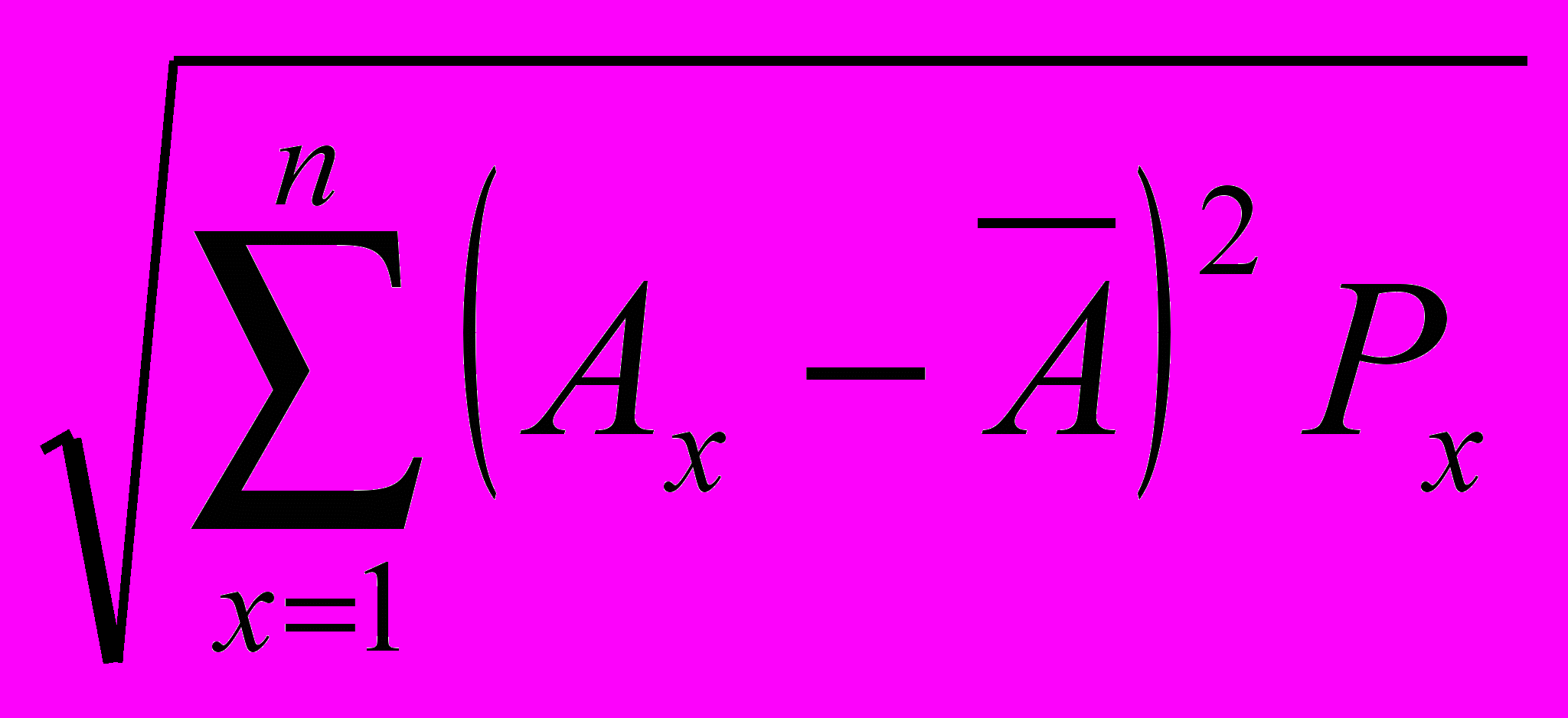,где
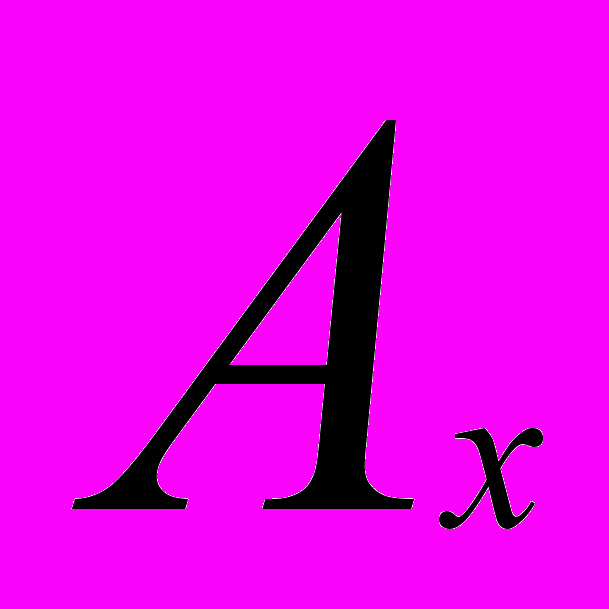-результат при конкретном уровне прибыли;
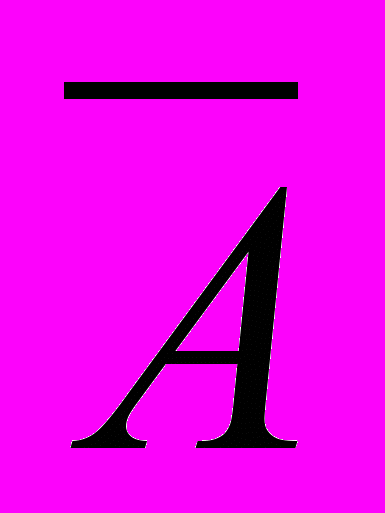- ожидаемое или среднее значение;
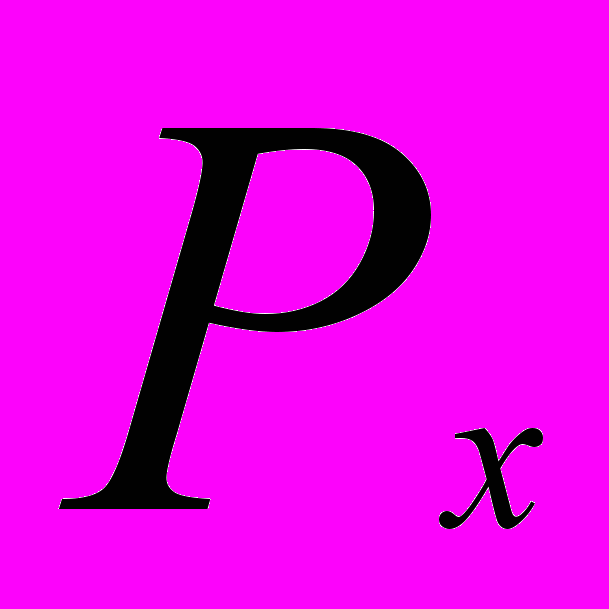-вероятность каждого исхода;n-общее число возможных вариантов;
суммирование осуществляется по всем возможным вариантом.
Квадрат среднеквадратического отклонения (
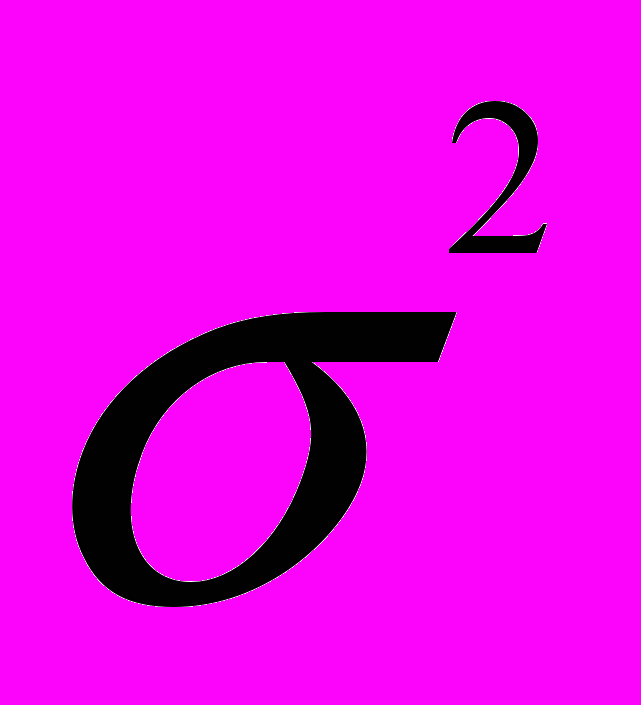) известен как статистическая дисперсия распределения и не должен смешиваться с отклонением от сметных или нормативных издержек. Вычисления среднеквадратических отклонений для продуктов А и В из примера показаны в таблицах 7, 8.Таблица 7 - Вычисление среднеквадратических отклонений.
Продукт А
| Прибыль | Отклонение от ожидаемого значения | Квадрат среднеквадратического отклонения | Вероятность | Взвешенное значение |
| 6000 | -2000 | 4000000 | 0,1 | 400000 |
| 7000 | -1000 | 1000000 | 0,2 | 200000 |
| 8000 | 0 | - | 0,4 | - |
| 9000 | 1000 | 1000000 | 0,2 | 200000 |
| 10000 | 2000 | 4000000 | 0,1 | 400000 |
| Сумма квадратов среднеквадратических отклонений | 1200000 | |||
| Среднеквадратическое отклонение | 1095,40 | |||
| Ожидаемое значение | 8000000 | |||
Сравнивать среднеквадратические отклонения двух распределений вероятностей с различными ожидаемыми значениями напрямую нельзя. Почему? Чтобы разобраться в этом, рассмотрим распределение вероятностей для другого продукта, например D. Среднеквадратическое отклонение для продукта D равно 21424 д. ед., хотя во всех возможных исходах результат в 10 раз больше соответствующих исходов для продукта В.
Исходы для продукта D имеют такой же тип распределения вероятностей, как и для продукта В, и можно бы предположить, что риск, связанный с этими двумя продуктами, будет одинаковым. Но среднеквадратическое отколонение у продукта Д в 10 раз больше, чем у продукта В. Этот эффект масштаба может быть устранен при помощи замены среднеквадратического отклонения относительным показателем дисперсии. Относительный показатель дисперсии может быть выражен коэфициентом вариации, который представляет собой сренеквадратическое отклонение, деленное на ожидаемое значение. Коэффициент вариации для продукта В равен 2142,40 / 8900=0,241 (или 24,1%), а для продукта D- также 0,241 (21 424/89000), что указывает на то, что для обойх продуктов относительное значение дисперсии является одинаковым.
Таблица 8 - Вычисление среднеквадратических отклонений.
Продукт В
| Прибыль | Отклонение от ожидаемого значения | Квадрат среднеквадратическое отклонение | Вероятность | Взвешенное значение |
| 4000 | -4900 | 24 010 000 | 0,05 | 1 200 000 |
| 6000 | -2900 | 8 410 000 | 0,10 | 841 000 |
| 8000 | -900 | 810 000 | 0,40 | 324 000 |
| 10000 | 1100 | 1 210 000 | 0,25 | 302 500 |
| 12000 | 3100 | 9 610 000 | 0,20 | 1 922 000 |
| Сумма квадратов среднеквадратических отклонения Среднеквадратическое отклонение Ожидаемое значение | 4 590 000 | |||
| 2142,40 | ||||
| 8900 | ||||
Таблица 9 - Распределение вероятностей для продукта D
| Исход по прибыли | Оцениваемая вероятность | Взвешенное значение |
| 40000 | 0,05 | 2000 |
| 60000 | 0,1 | 6000 |
| 80000 | 0,4 | 32000 |
| 100000 | 0,25 | 25000 |
| 120000 | 0,2 | 24000 |
| | 1,0 | 89000(ожидаемое значение) |
В ходе проведенных рассуждений до сих пор риск определялся в единицах разброса возможных исходов, т.е. риск может быть большим даже в том случае, если все возможные исходы связаны с получением высокой прибыли. Однако риск, присущий возможным прибылям или убыткам, полученный при другом варианте действий, является не дисперсией как таковой, а прежде всего вероятностью того, что отклонения будут ниже ожидаемого значения. В данном случае лицо, принимающее решение, вряд ли станет рассматривать большие возможные отклонения, превышающие ожидаемое значение, как нежелательные (поскольку тогда просто прибыль будет больше). Рассмотрим следующие распределения вероятностей.
Среднеквадратические отклонения составляют д. ед.1342 для продукта Х и д. ед.2227-для У, что дает значения коэффициентов вариаций соответственно 0,19 (Х) и 0,28 (У). Эти показатели свидетельствуют о том, что оценкии для продукта У подвержены большей изменчивости, однако скорее всего продукт Х относится к категории с более высоким риском, так как вероятность того, что прибыль будет ниже д. ед.7000 (ожидаемое значенние Х), равна 0,4 для х и 0,2-для У. Понятно, что среднеквадратическое отклонение и коэффициент вариации не являются совершенными показателями риска, однако математические трудности измерения того, что эти отклонения ниже по величине ожидаемого значения,обычно очень значительны, если не говорит о самых простых случаях. Можно сказать, что ожидаемое значения, среднеквадратические отклонения и коэффициенты вариации используются для выражения обобщенных характеристик альтернативных вариантов действий, но сами по себе являются плохими заменителями для представления распределений вероятностей, так как не дают лицу, принимающему решение, всей релевантной информации. Поэтому появляется аргумент, чтобы предоставлять лицу, принимающему решение, непосредственно все распределение вероятностей. Такой подход вполне пригоден, когда менеджеры могут выбирать из небольшого числа альтернативных вариантов, но в ситуациях, когда вариантов возможных действий, которые необходимо рассмотреть, очень много; анализ многих распределений вероятностей скорее всего будет трудным и потребует много времени. В этих условиях у менеджеров может не оказаться большого выбора с точки зрения применяемых методов, и им ничего не останется, кроме сравнения ожидаемых значений и коэффициентов вариации.
Таблица 10 - Распределение вероятностей для продукта Х
| Исход по прибыли | Оцениваемая вероятность | Взвешенное значение |
| 40000 | 0,1 | 400 |
| 60000 | 0,3 | 1800 |
| 80000 | 0,6 | 4800 |
| | 1,0 | 7000(ожидаемое значение) |
Таблица 11 - Распределение вероятностей для продукта У
| Исход по прибыли | Оцениваемая вероятность | Взвешенное значение |
| 6000 | 0,2 | 1200 |
| 8000 | 0,5 | 4000 |
| 12000 | 0,3 | 3600 |
| | 1,0 | 8800(ожидаемое значение) |
Как определить, является выбранный вариант действий рикованным или нет? Ответ на этот вопрос зависит от отношения к риску лица, принимающего решение. Можно выделить три возможных отношения к риску: отрицательное, положительное и нейтральное. Рассмотрим два варианта - А и В, которые характеризуются следующими возможными исходами в зависимости от состояния экономики (т.е. внешними условиями).