Управление рисками

Вид материала

Содержание

Функция полезности
Функция полезности
2.3 Вид функций полезности и рискованные решения
Контрольные вопросы

Подобный материал:

1 2 3 4 5 6 7 8 9

Функция полезности

Проигрыш Выигрыш

Вредность

проигрыша

Рисунок 1 - График функции полезности риска при ровном отношении

При ровном отношении к риску полезность выигрыша равна этой сумме П(C) = C, П(-в) = - в.

Ожидаемый выигрыш страховой компании может быть таким:

если авария произойдет, то страховая компания должна выплатить премию и удовлетвориться получением страхового взноса, ее выигрыш отрицателен и равен р (- С + в);
если аварии не будет, то выигрыш страховой компании за счет страхового взноса, который положителен, составит (1 - Р) в.

Страховая компания будет идти на риск, если общая сумма ее выигрыша положительна:

р (- С + в) + (1 – Р) в > 0 (5)

при в > рС (условие заключения договора страховой компанией).

Полезность риска при страховании имущества для его владельца может быть определена так. Если заключается договор о страховании, то полезность выигрыша П(-в) равна риску потери сравнительно небольшой суммы страхового взноса. Если договора нет, то полезность выигрыша составляет рП(-С), т.е. равна риску потерять значительно большую сумму. идти на риск страхования следует, если П(-в)-РП(-С) > 0, т.е. риск оправдан, если рискуя меньшим, избегаем больших потерь.

При ровном отношении к риску из неравенства П(-в) – рП(-С) > 0 следует, что -в + рС > 0 и в < рС, а это неравенство противоречит условиям страхования (в < рС), поэтому при ровном отношении к риску страхования не будет вовсе, риск не имеет смысла.

Полезность

выигрыша

Функция

полезности

Проигрыш Выигрыш

Вредность

Проигрыша

Рисунок 2 - График функции полезности риска при осторожном отношении

Но ровное отношение к риску не только не единственное, но и не самое распространенное. Люди оценивают полезность выигрыша и вредность проигрыша не пропорционально их величине. Для осторожного (не расположенного к риску) отношения характерно опасение больших проигрышей.

Вредность больших проигрышей преувеличивается, а соответствующая полезность выигрышей преуменьшается. Соответствующий риск называется осторожным. Функция полезности при осторожном отношении к риску, показанная на рисунке 2, имеет вид: П(в) = 1-е ^–в . П(в) – вероятность появления не менее одного выигрыша, если выигрыш – редкое событие. Формула получена на основе теории вероятностей.

При осторожном отношении полезность общего результата для владельца имуществом складывается из полезности выигрыша и проигрыша и равна

П(в) = П(-в) – р · П(-С) = 1-е ^b – р(1-е^с) (6)

На риск следует идти, если общий результат окажется положительным, т.е. П(в) > 0:

1-е^b-р(1-е^с) > 0;

-p(1-e^c) > e^b - 1;

p(e-1) > e^b - 1;

P > (e^b-1) / (e^c-1).

Это условие страхования для имущества при осторожном отношении к риску, а p < b / c – условие заключения договора страховой компанией.

Отсюда следует, что страхование состоится, если вероятность аварии равна

b / c > p > ( e^b - 1) / (e^c-1) (7)

При предполагаемой вероятности аварии осторожный владелец будет страховать имущество при определенном соотношении между размером страхового взноса и страховой премии.

Смелое (расположенное к риску) отношение характерно тем, что малые выигрыши считаются почти бесполезными, а полезность больших выигрышей не пропорционально увеличивается. Вероятность больших проигрышей сильно преуменьшается. Соответствующий риск называется смелым и представлен на рисунке 3.

Функция полезности риска при смелом отношении имеет вид

П(В) = е^b-1 (8)

Она получена по формуле сложных процентов.

При смелом отношении к риску решение о страховании будет принято владельцем имущества, если общая полезность выигрыша и проигрыша будет положительна:

П(в) = П(-в) – р · П(-С) > 0;

e^-^b- 1 - p(e^-^c-1) > 0;

p < (e^-b-1) / (e^-c-1).

Условие страхования при смелом отношении к риску для владельца имущества таково:

p < (e^-b-1) / (e^-c-1) (9)

Полезность

выигрыша

Функция полезности

Проигрыш Выигрыш

Вредность

проигрыша

Рисунок 3 - График функции полезности риска при смелом отношении

Вероятность аварии (р) изменяется от 0 до 1. Сумма страховой премии принята за единицу (с =1), а величина страхового взноса (в) изменяется от 0 до 1 усл.ед.

Кривая совмещенных графиков, соответствующая смелому отношению к риску, проходит слева от линии, соответствующей требованию страховой конторы, т.е. в области, где страхование для конторы нецелесообразно. Интересы владельца имущества и страховой конторы нигде не совпадают, следовательно, при смелом отношении к риску страхование не состоится вообще.

Еще одной моделью с использованием функций полезности может служить «задача о вознаграждении при действии на удачу», например, покупка дополнительного оборудования, относительно которого нет твердой уверенности в том, что оно обязательно понадобится. Но если произойдет какое-то событие (пожар, необходимость эвакуации, срочная погрузка с использованием подъемно-транспортного средства и т.п.), то сравнительно недорогое оборудование даст значительный выигрыш или предотвратит. Стремление получить значительный выигрыш сравнительно малыми средствами характерно для этой ситуации, которую относят к ситуации риска по типу лотереи.

Пусть Л – стоимость лотерейного билета (стоимость оборудования, которое будет куплено при принятии решения о целесообразности риска, р - вероятность выигрыша; Д – сумма выигрыша (она возвращает стоимость билета, купленного оборудования, которое представляет собой материальную ценность).

Выигрыш организатора лотереи (в) складывается так:

если билет выигрывает, то его выигрыш отрицателен: р(-Д);
если билет не выигрывает, то за счет продажи билетов выигрыш составит (1-р) Л.

Организатор станет рисковать, если общий результат окажется положительным:

В=р(-Д)+(1-р)Л, В>0, Л>p(Д+Л) (10)

Тогда -рД+Л-рЛ>0: p<Л/(Д+Л) – это условие организатора лотореи.

Если р=0,001 (1 билет из 1000 выигрывает), то 0,001>Л/(Д+Л), 0,001=1/(999+1). Д=299, Л=1, т.е. стоимость билета должна быть не менее, чем 1/999 от размера выигрыша.

Выигрыш обладателя билета будет таким:

если билет выигрывает, то размер выигрыша рД;
если билет не выигрывает, то проигрыш равен (1-р) (-Л).

Общий выигрыш составит

В_в.б=рД+(1-р) (-Л)=рД-Л+рЛ=Л+р(Д+Л) (11)

Отсюда р>Л/(Д+Л).

А так как организатор устраивает лотерею, при р>Л/(Д+Л), то владелец билета всегда будет получать средний выигрыш отрицательный, т.е. в среднем он будет в проигрыше.

Тогда встает вопрос о бесполезности риска. Но все зависит от отношения владельца билета к ожидаемому выигрышу. Для принятия решения о риске по типу лотереи денежный выигрыш равен 1 усл. ед. (Д=1), вероятность выигрыша изменяется от 8 до 1, а стоимость билета – от 0 до 1 усл. ед.

При ровном отношении к риску полезность выигрыша для владельца билета составит П(В)=В_в.б=-Л+р(Д+Л).

Предельное отношение функции полезности при ровном отношении к риску будет при р=Л/(Д+Л). Но владелец билета будет рисковать, если его выигрыш положителен:

В_в.б=-Л+р(Д+Л), В_в.б>0

Отсюда р(Д+Л) >Л.

А это противоречит условию устройства лотереи организатором, который требует, чтобы Л >р(Д+Л). Следовательно, при ровном отношении риск не оправдан. Не оправдан он и при осторожном отношении к риску. Полезность общего результата владельца билета будет в этом случае:

П(В_в.б)=П(рД+(1-р) (-Л))=П(рД)+П((1-р)(-Л))=р(1-е^-Д)+(1-р) (1-е^Л)

Она должна быть положительной:

р(1-е^-Д)+(1-р) (1-е^Л) >0 (12)

Отсюда р > (е^Л-1) / (е^Л-е^-Д). Так как эта линия находится слева от линии ровного отношения, а область благоприятного риска находится справа от нее, то при осторожном отношении риск покупки билета не оправдан.

При смелом отношении к риску полезность выигрыша владельца билета составит:

П(В_в.б)=П(рД)+П((1-р) (-Л));

П(В_в.б)= р(1-е^-Д)+(1-р) (1-е^Л).

Полезность общего результат должна быть положительной:

р(е^Д-1)+(1-р) (е^-Л -1) >0;

р > (1-е^-Л) / (е^Д - е^-Л).

Смелому отношению к риску соответствует линия, которая показывает граничное значение р = (1- е^-Л) / (е^-Д -е^Л). Эта линия находится справа от линии ровного отношения.

Поэтому при смелом отношении к риску покупать билеты целесообразно, если

1-е^-Л

< р < Л / Д + Л (13)

е^Д-е^-Л

Например, если р=0,2, то стоит рискнуть в том случае, если стоимость билета составляет от 0,25 до 0,6 усл. ед. Если выигрыш составляет 100000 усл. ед, то покупка целесообразна при стоимости билета от 2500 до 60500 усл. ед.

Таким образом, рассмотрев два типовых случая, можно систематизировать основные выводы о принятии решений.

Таблица 1 - Варианты принятия решений

Отношение к выигрышу и проигрышу (вид функции полезности риска)	Решение о риске в ситуации
	По типу страхования	По типу лотереи
Ровное	Не рисковать	Не рисковать
Осторожное	Рисковать (при определенных условиях)	Не рисковать
Смелое	Не рисковать	Рисковать (при определенных условиях)

2.3 ВИД ФУНКЦИЙ ПОЛЕЗНОСТИ И РИСКОВАННЫЕ РЕШЕНИЯ

Кроме ровного, осторожного и смелого отношений, полезность риска может быть выражена и другими видами функций. Некоторые из этих функций полезности риска называют: отношение «сильного», отношение «слабого», «гибкое» отношение, «призовое» отношение, «целевое» отношение.

Отношение «сильного» характеризуется тем, что преуменьшается как полезность выигрышей, так и вредность проигрышей. Поэтому эта функция полезности представляет собой сочетание функций, соответствующих осторожному (при проигрыше) и смелому (при выигрыше) отношениям.

«Гибкое» отношение характеризуется тем, что для небольших выигрышей и проигрышей функция полезности риска показывает смелое отношение, а для больших – осторожное.

«Призовое» отношение – это такое, при котором, кроме полезности выигрыша (вредности проигрыша) учитывается дополнительный приз за выигрыш и дополнительные потери при проигрыше. Это могут быть и денежные премии, призы, штрафы и т.п.

«Целевое» отношение – это такое, при котором целью всех действий, сопряженных с риском, является достижение определенного выигрыша. Только такой выигрыш считается полезным, а далее полезность его постоянна. Меньше значение выигрыша (как и большее - проигрыша) никакой полезности (для проигрыша – вредности не представляет. Это может быть необходимость выполнения определенного задания, плана, программы и т.д.

40

С Д

30

В

20

А

10

Полезность УЕ

0 50 100 150 200 Доход, тыс.уе

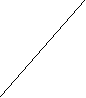
Рисунок 4 - Функция полезности и антипатия к риску

Существуют условия, определяющие вид функции полезности. Во-первых, он зависит от состояния дел того, кто собирается рисковать. Если ограничены, то, вероятнее всего, будет преобладать отношение «слабого»: большие выигрыши и проигрыши будут казаться еще больше. Если же средства велики, то можно ожидать отношения «сильного». Во-вторых, вид функции полезности обусловлен целью идущего на риск: если нужно выиграть во что бы то ни стало, то характерно «целевое» отношение к риску. В-третьих, на вид функции полезности влияют субъективные данные идущего на риск: его характер, темперамент, моральное состояние, получаемое удовольствие от самого процесса, азарт и др. Об этом говорят и названия некоторых видов отношений к риску: осторожное, смелое, ровное, гибкое, целевое.

От выбора связанных с риском альтернативных вариантов потребители получают определенную полезность, измерения которой удобно представить в условных единицах – УЕ, хотя на практике такие измерения невозможны.

Например, функция полезности при осторожном отношении к риску (антипатия к риску) может показывать уровень полезности, измеренный в условных единицах и достигаемый при каждом уровне дохода.

Когда доход увеличивается с 50 до 100 тыс. ед. предельная полезность уменьшается с 20 до 10 УЕ, а, когда доход поднимается со 100 до 150 тыс. ед. – до 3. По мере увеличения дохода общая полезность тоже возрастает, но каждые новые 50 тыс. ед. дохода добавляют к общей предельной полезности.

Предположим, что субъект может выбирать работу со стабильным доходом в 100 тыс. ед. с вероятностью 0,5 и доходом 50 тыс. ед. с той же вероятностью (так что ожидаемый доход составляет 100 тыс. ед.): (150·0,5+50·0,5=75+25=100). Ожидаемая полезность неопределенного дохода равна : 20·0,5+33·0,5=26,5 УЕ.

Сравним ожидаемую полезность при работе, связанной с риском, с полезностью при доходе в 100 тыс. ед. без риска. Уровень полезности дан точкой В и равен 30 УЕ. Он больше, чем ожидаемая полезность при работе с риском, поэтому будет выбрана работа, приносящая меньший, но стабильный доход.

40

С

Полезность УЕ

30

В

20

А

10 О

0

50 100 150 200

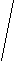
Рисунок 5 - Функция полезности и расположенность к риску

Реальный опыт, основанный на многочисленных специальных экспериментах, говорит, что большинство субъектов экономики (индивидуумы, фирмы и т.п.) склонны к стабильности. Они предпочитают вариант, приносящий стабильный доход, варианту, связанному с риском. В то же время средние значения (математические ожидания) дохода одни и те же.

Если не любящий риск субъект экономики предпочтет детерминированный доход случайному, то максимальная сумма, которую он готов заплатить, чтобы избежать риска, является вознаграждением за риск.

В случае расположенности к риску ожидаемая полезность определенного дохода, который может составить 50 тыс. ед. с вероятностью 0,5 или 150 тыс. ед. с той же вероятностью, выше, чем полезность определенного дохода в 100 тыс. ед., равная 10 УЕ. В числовом выражении полезность неопределенного дохода составит:

0,5·+0,5·22=2+11=13 УЕ.

При смелом отношении к риску будет выбрана работа, связанная с риском неопределенного дохода.

При нейтральном (безразличном, ровном, спокойном) отношении к риску человек безразличен к заработку со стабильным и неопределенным доходом, если неопределенный доход равен ожидаемому доходу.

Полезность связанная с работой, дающей доход 50 тыс. ед. или 150 тыс. ед. с равной вероятностью (рисунок 6), составляет 20 УЕ.

0,5·10+0,5·30=5+15=20

40 Д

Полезность УЕ

30

С

20

В

10

А

О

0 50 100 150 200 Доход

Рисунок 6 - Функция полезности и безразличия к риску

Полезность при получении стабильного дохода в 100 тыс. ед. тоже равна 20 УЕ (точка В). Неопределенный доход, как уже отмечалось, равен ожидаемому доходу в 100 тыс. ед.:

0,5·50+0,5·150=100

Человек, относящийся безразлично как к стабильному доходу, так и к рискованному с одинаковым ожидаемым значением, является безразличным к риску.

Анализируя выбор в условиях риска, М.Фридмэн и Л. Сэвэдж отметили следующие свойства функции полезности. Она возрастает вместе с доходом (предельная полезность ожидаемого дохода везде положительна). Если кривая полезности находится ниже некоего уровня дохода, то она будет выпуклой сверху, вогнутой на промежутке от текущего до более высокого дохода и вновь выпуклой для всех еще более высоких доходов. Это означает, что предельная полезность является убывающей на изначальном выпуклом сегменте, возрастает на вогнутом сегменте и убывает на верхнем выпуклом сегменте. Большинство потребителей имеет тенденцию выбора деятельности, доходы от которой позволяют им размещаться в тех сегментах кривой, где предельная полезность дохода убывает.

Выпуклость функции полезности вниз (вверх) отражает склонность (не склонность) к риску.

Анализируя различные функции полезности, авторы работы пришли к выходу, что в общем случае функции полезности должна:

в зоне умеренных доходов быть близкой к линейной;
в зоне больших доходов – существенно «пологой» (эффект насыщения);
в зоне большого ущерба резко возрастать по абсолютной величине, а затем, возможно, переходить в почти постоянную функцию, что побуждает к уменьшению вероятности срыва, разорения (и это означает, в частности, отказ от ориентации на средне значение).

С помощью функций полезности можно установить, при каких условиях стоит рисковать, а при каких нет. Или может быть обратная задача: зная условиях риска, определить, при каких функциях полезности можно ожидать рискованных действий, а при каких нет. Рискующий сопоставляет шансы на успех и неудачу, и если это соотношение его устраивает, то он идет на риск. Оценка соотношения шансов производится с учетом полезности, субъективной ценности той или иной степени успеха или неудачи. Полезность определяется главным образом, состоянием дел рискующего и его задачами. На риск он пойдет тогда когда полезность выигрыша больше опасности проигрыша.

Следует отметить, что получаемый с помощью рискованных действий некоторый положительный итог имеет место не в каждом отдельном случае, а в среднем в конечном результате многих рискованных действий.

КОНТРОЛЬНЫЕ ВОПРОСЫ

Что такое «полезность альтернатив»?
Какую альтернативу выбирает потребитель при отсутствии и при наличии риска?
Что такое «полезность риска»?
От чего зависит принятие решения: идти или нет на риск?
Почему при нейтральном (ровном, безразличном, простейшем) отношении к риску владелец имущества не станет его страховать?
Чем характерно осторожное отношение к риску и всегда ли владелец имущества захочет его застраховать?
Почему при смелом отношении к риску страхование вообще не состоится?
Какие ситуации относятся к ситуации риска по типу лотереи?
При каком отношении к риску будет принято решение рисковать и при каком не рисковать в ситуации по типу лотереи?
Как выглядит график функции полезности риска при отношении «сильного» и в каких случаях можно ожидать подобного отношения?
Чем характеризуется график функции полезности риск при отношении «слабого» и какие условия определяют вид этой функции полезности?
Как выглядит график функции полезности риска можно выделить и чем они характеризуются?
Какие еще функции полезности риска можно выделить и чем они характеризуются?
Какие факторы определяют вид функции полезности риска?
В каком случае субъект предпочтет стабильный доход определенного размера равному по размеру, по связанному с риском доходу?
Что является критерием выбора для потребителей?
При какой функции полезности риска субъект относится одинаково как к стабильному доходу, так и к рискованному с одинаковым ожидаемым значением?
Какой потребитель и при какой функции полезности предпочтет связанный с риском доход стабильному получению этой ожидаемой суммы? Почему он так поступил?
Почему при расположенности к риску выбирается вариант (работа, капиталовложения, ценные бумаги и т.д.), связанный с риском неопределенного дохода?
Что такое вознаграждение за риск?

Blog

Управление рисками

Содержание

Функция полезности

Функция полезности