Задача дирихле для фрактального уравнения лапласа в прямоугольной области масаева О. Х

Вид материала

Задача

Подобный материал:

• Уравнения математической физики Лектор 2010/11 уч года д ф. м наук, и о. проф. Косимов, 67.08kb.
• Секция 7 А. Н. Васильев, Д. а тархов, 79.95kb.
• Вопросы к экзамену по учебной дисциплине «Дифференциальные уравнения», 32.43kb.
• Задача Коши для одномерного уравнения Даламбера. Формула Даламбера, 45.74kb.
• Рабочая программа дисциплины уравнения в конечных разностях направление подготовки, 90.19kb.
• Календарный план чтения лекций, 27.51kb.
• Дифференциальные уравнения (вопросы к экзамену), 26.43kb.
• Содержание курса (лекции), 49kb.
• Задача Коши для неоднородного уравнения с однородными граничными условиями, 80.58kb.
• Лекции Число часов, 51.1kb.

ЗАДАЧА ДИРИХЛЕ ДЛЯ ФРАКТАЛЬНОГО УРАВНЕНИЯ ЛАПЛАСА В ПРЯМОУГОЛЬНОЙ ОБЛАСТИ

Масаева О.Х.

Учреждение Российской академии наук Научно – исследовательский институт прикладной математики и автоматизации КБНЦ РАН, Нальчик

1. Введение. Рассмотрим уравнение
   

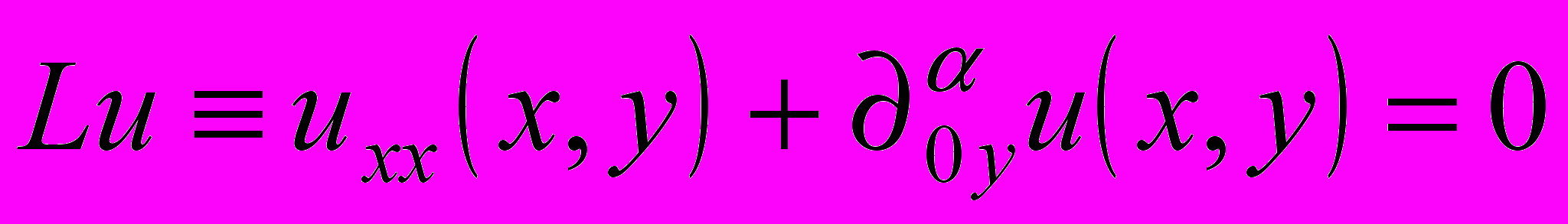, (1)

где 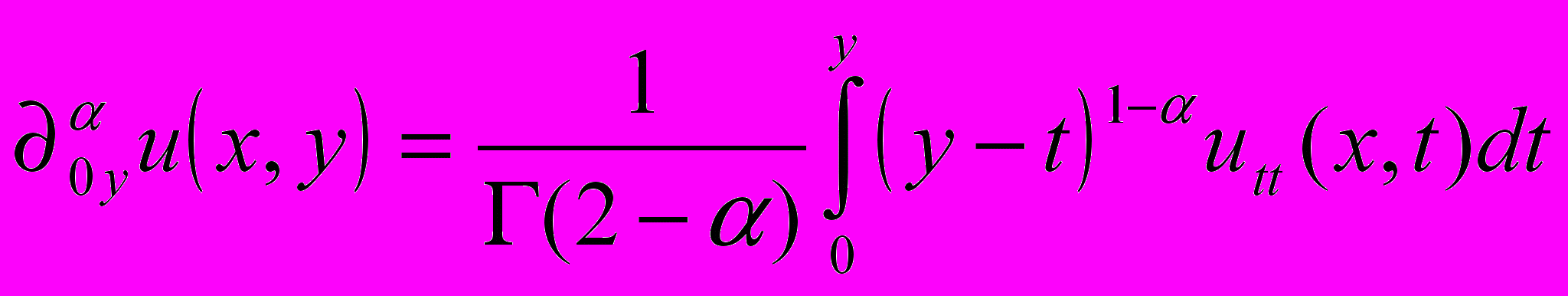- производная Капуто порядка 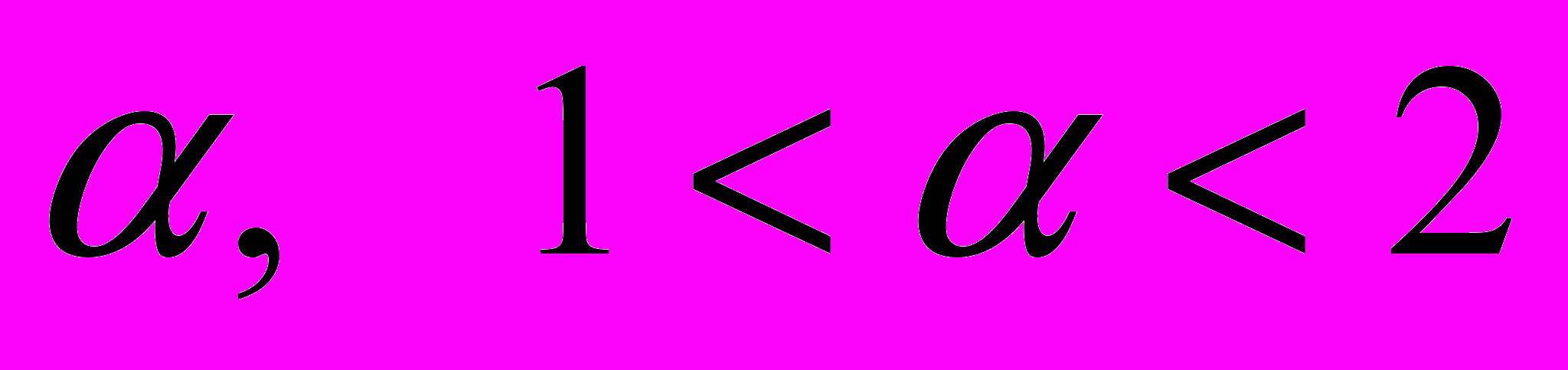, [1, c.11].

Оператор 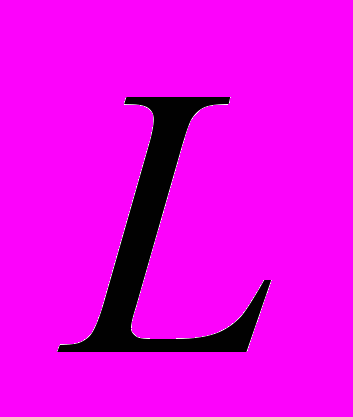совпадает с оператором Лапласа при 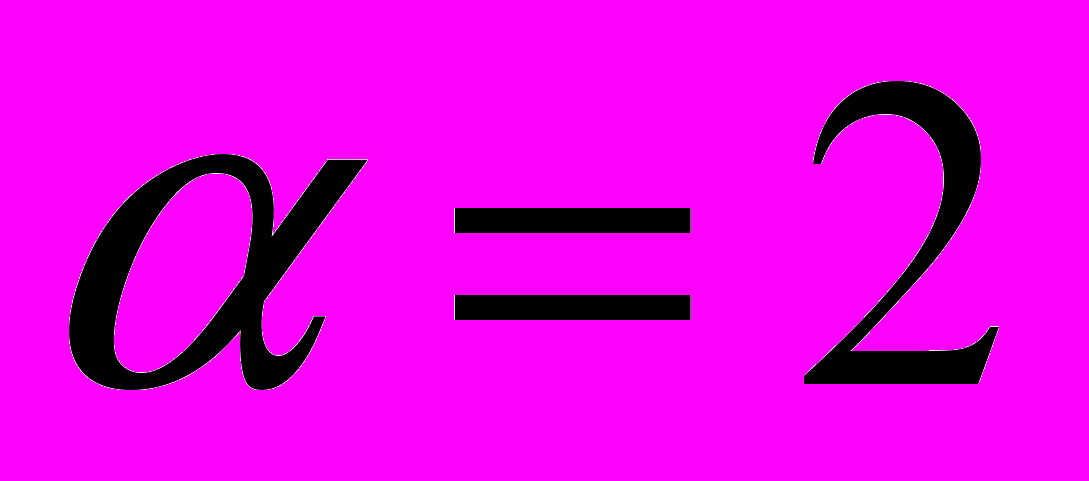и обобщает его на нецелые значения порядка производной по переменной .

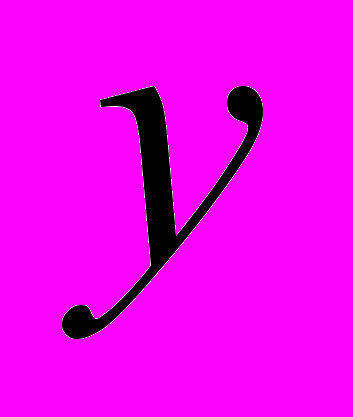Необходимость исследования краевых задач для уравнения (1) определяется использованием фрактального уравнения Лапласа для описания производственных процессов при математическом моделировании социально-экономических систем [2].

В работе [3] методами теории потенциалов исследованы основные граничные задачи для трехмерного уравнения Лапласа дробного порядка. В работе [4] доказана корректность по Адамару аналога задачи Дирихле для уравнения



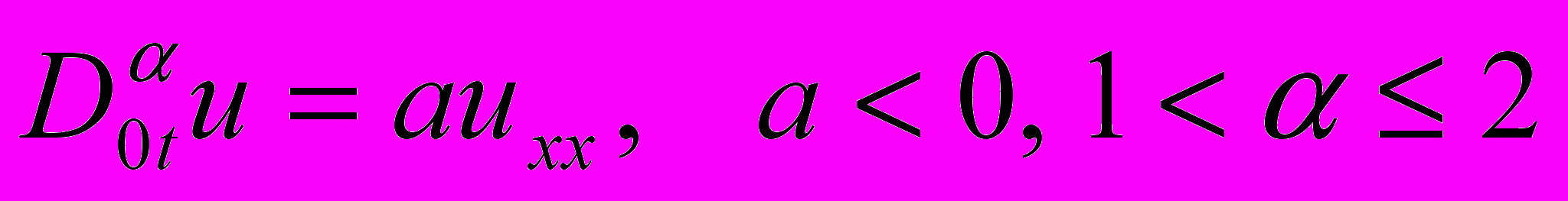
в прямоугольной области, где 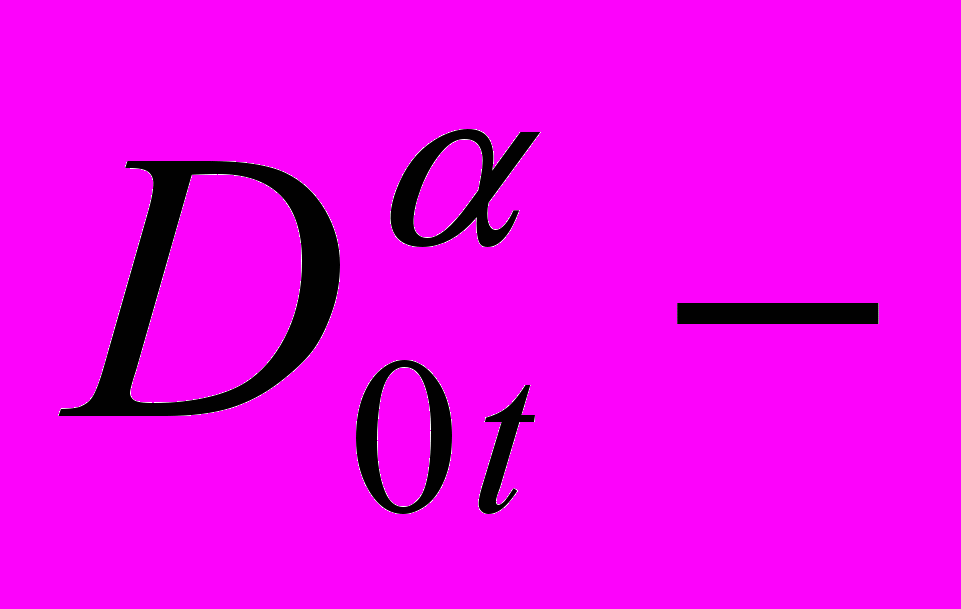оператор дробного дифференцирования Римана-Лиувилля [1, c. 9].

В данной работе методом Фурье строится решение задачи Дирихле для уравнения (1) в прямоугольной области и предложенным в работе [5] методом доказывается единственность решения.

2. Постановка задачи. Регулярным решением уравнения (1) в области 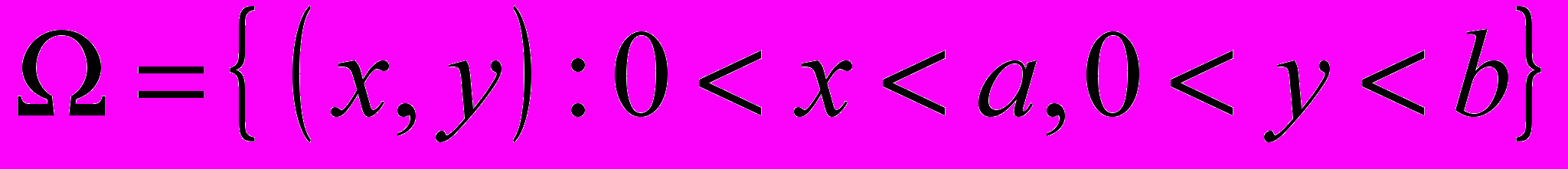назовем функцию 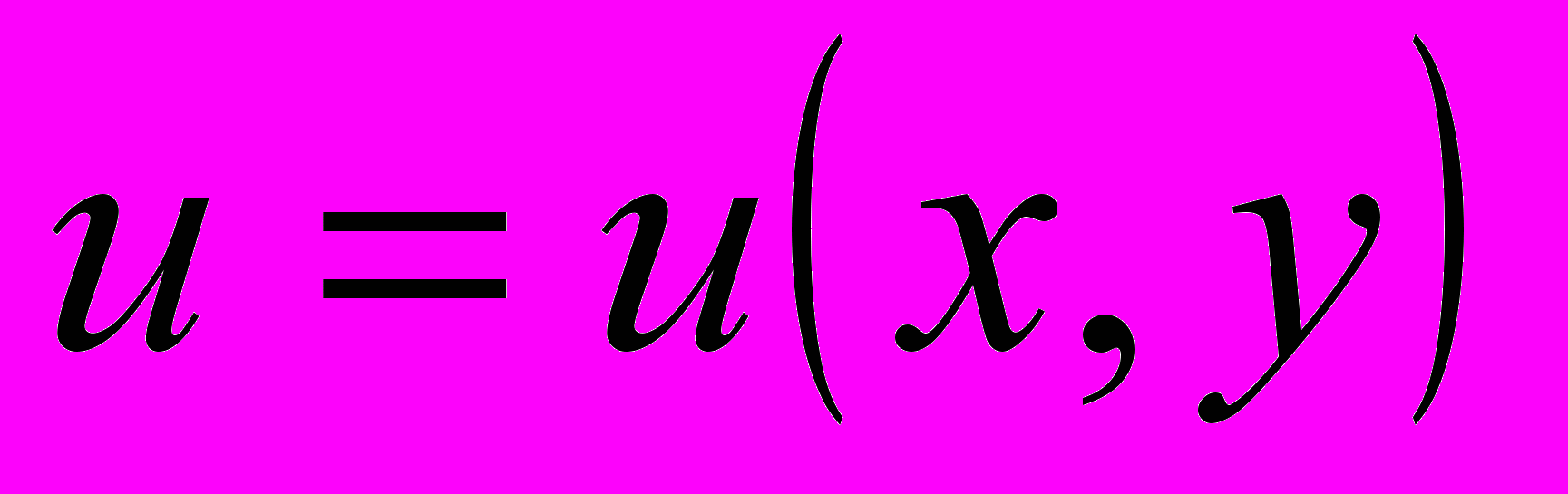такую, что 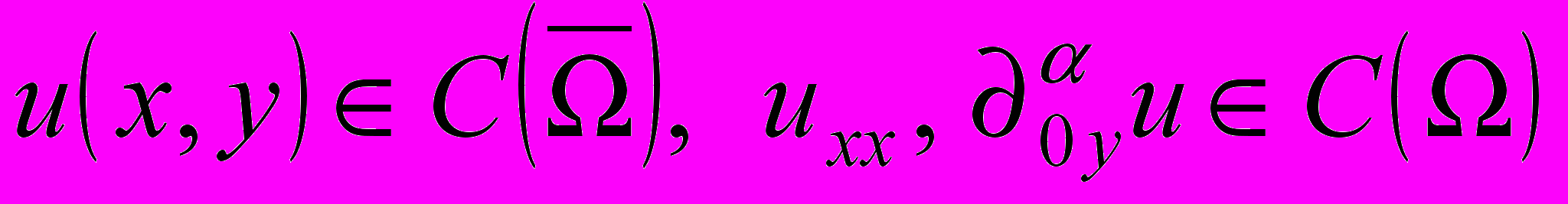и удовлетворяющую уравнению (1) во всех точках .
   

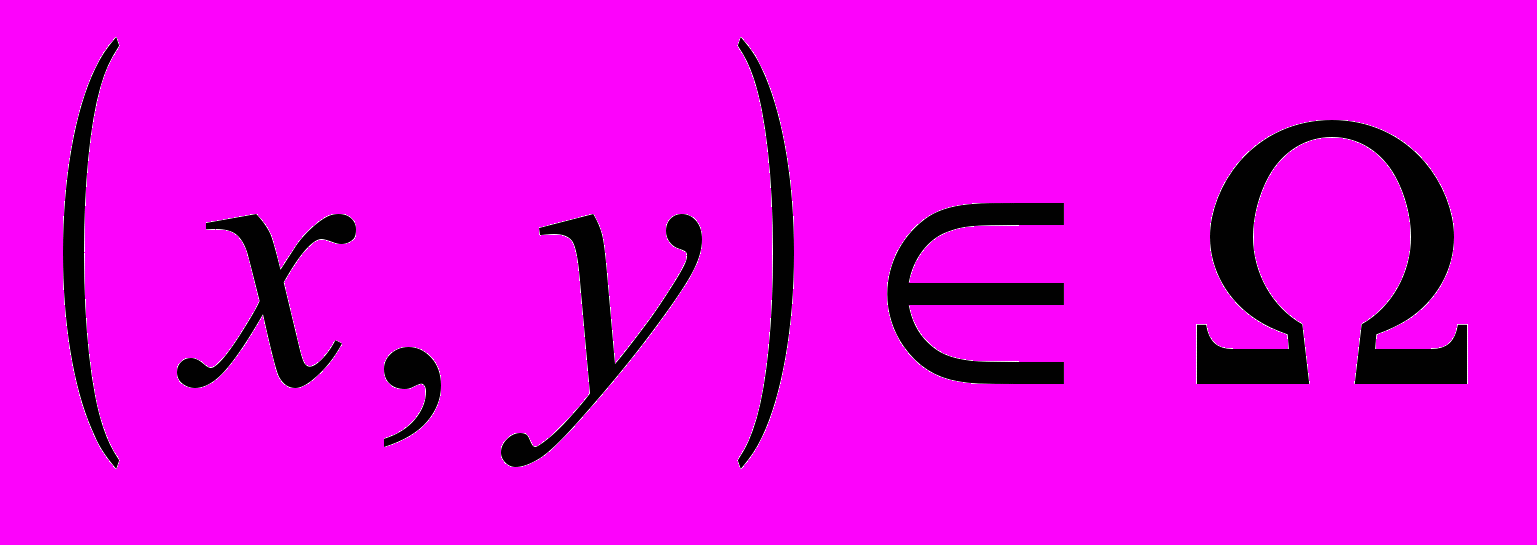Задача Дирихле. Найти регулярное решение уравнения (1) удовлетворяющее краевым условиям

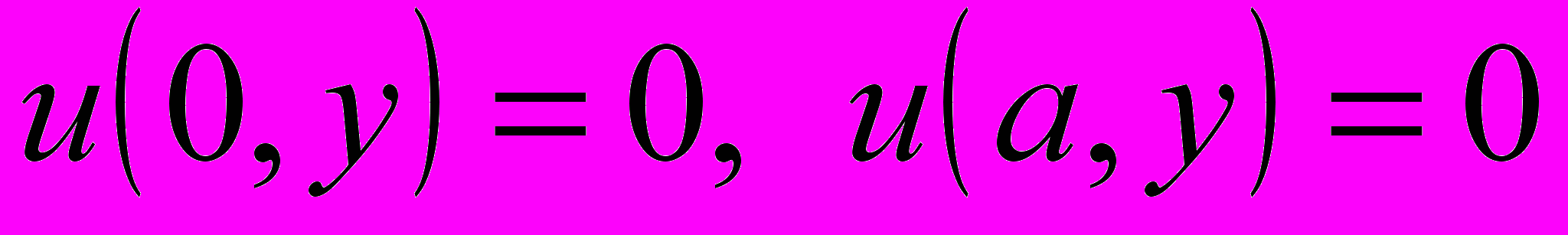, (2)

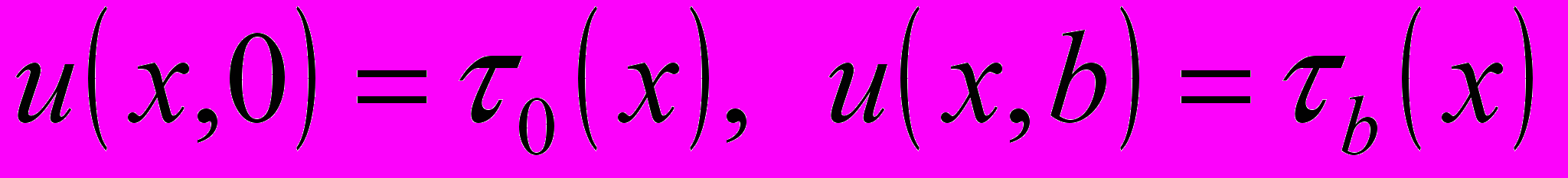, (3)

где 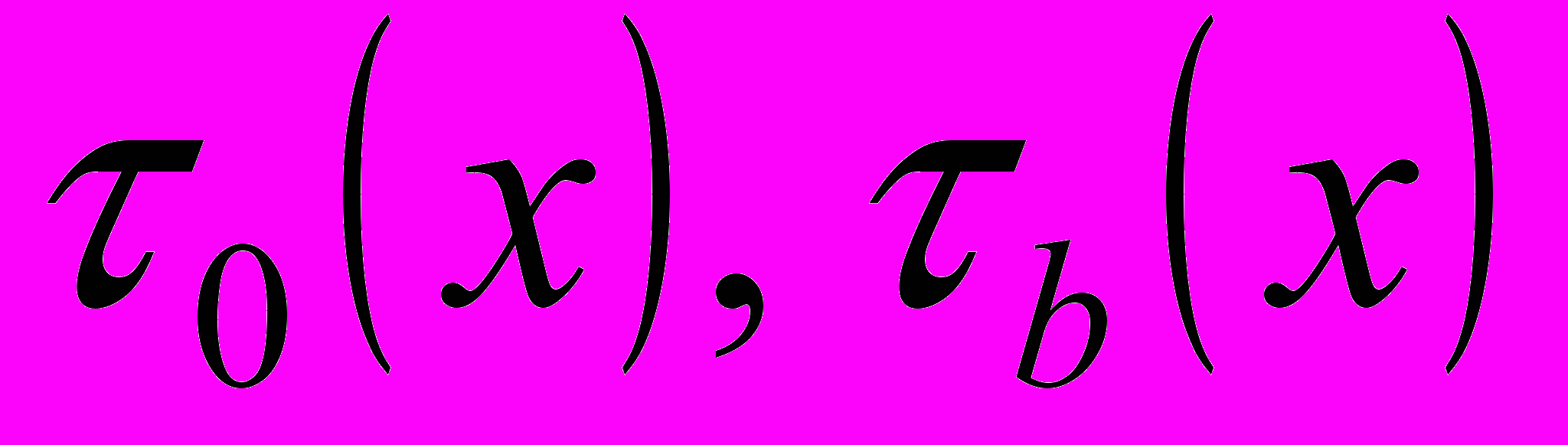- заданные функции.

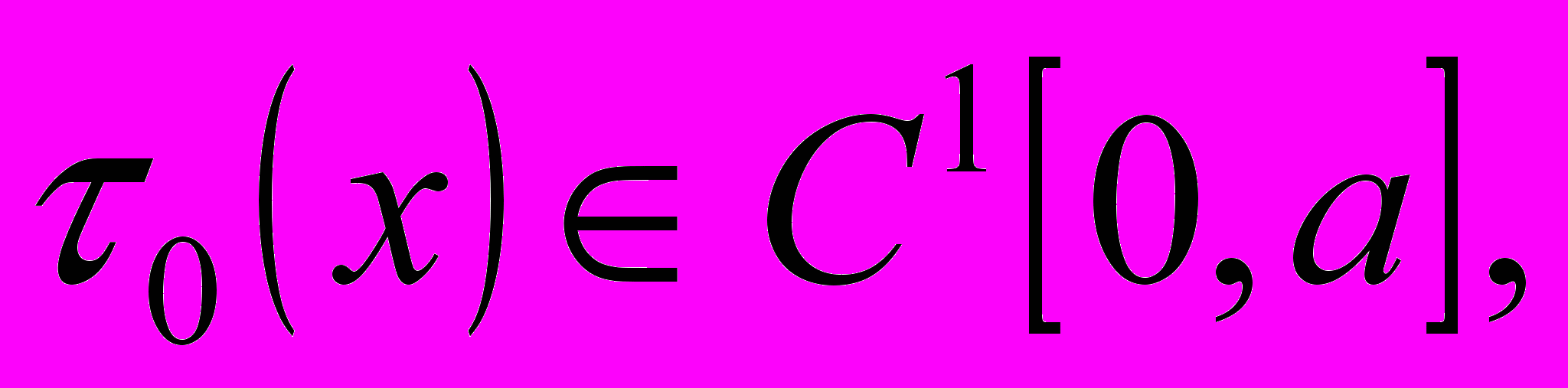
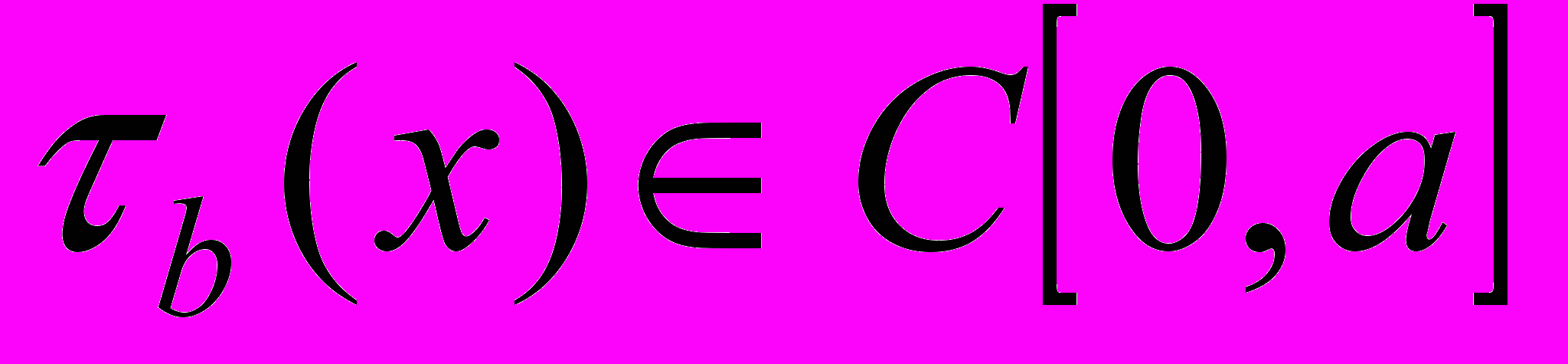
Теорема 1. Если 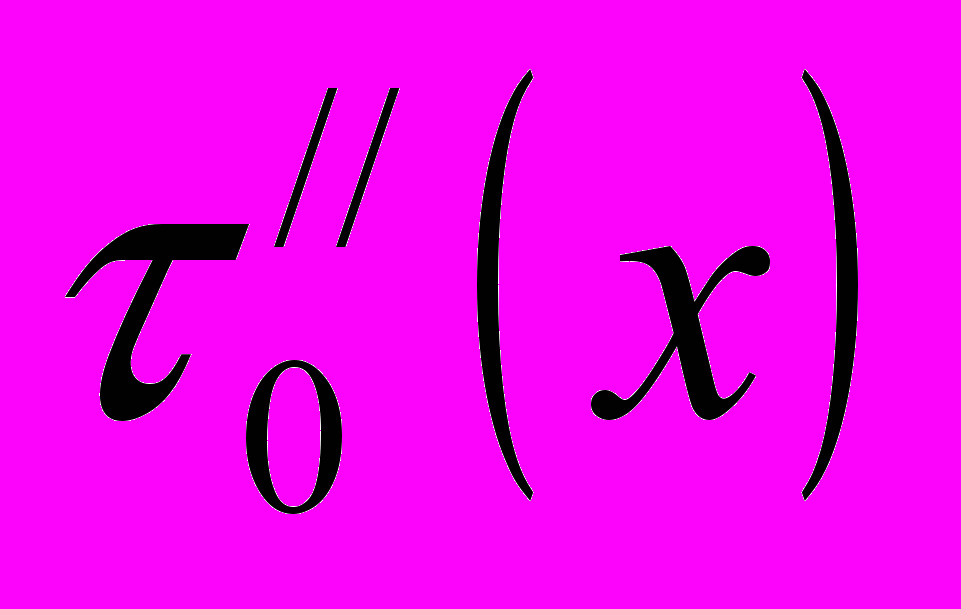,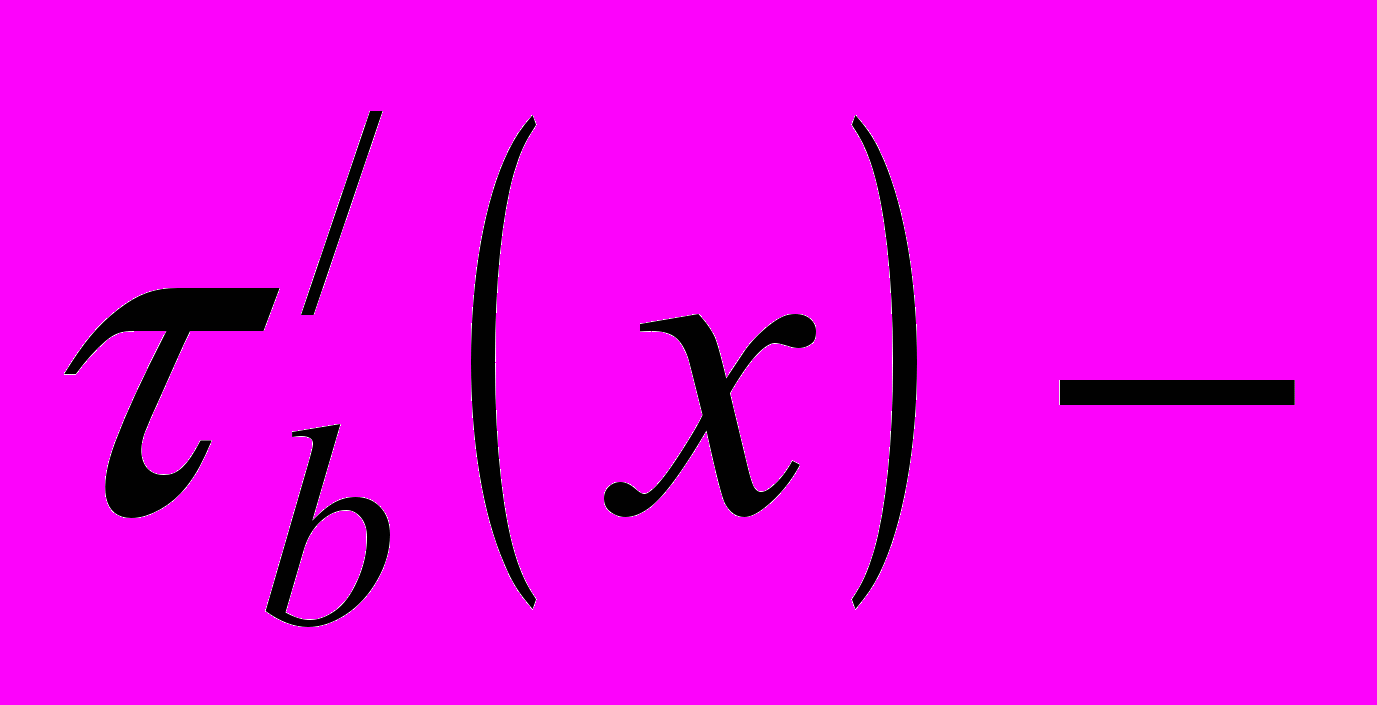кусочно-непрерывны и кусочно-монотонны в промежутке 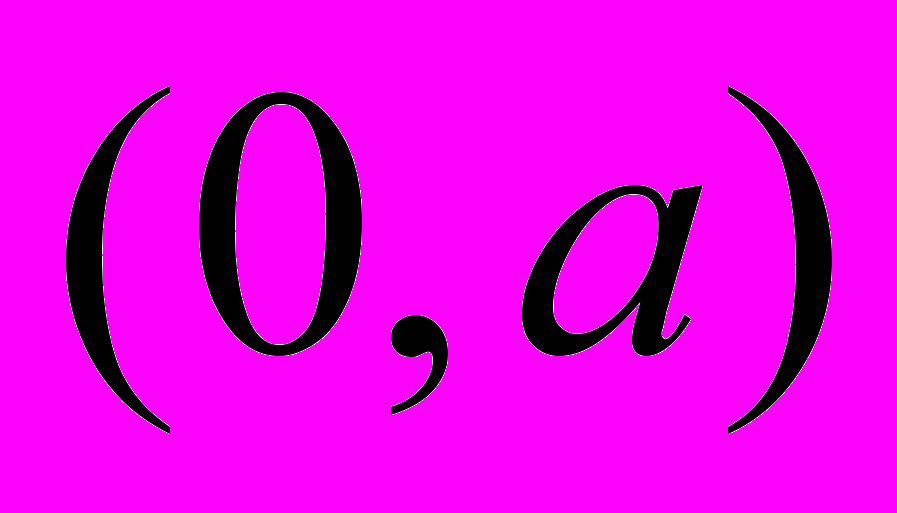, , 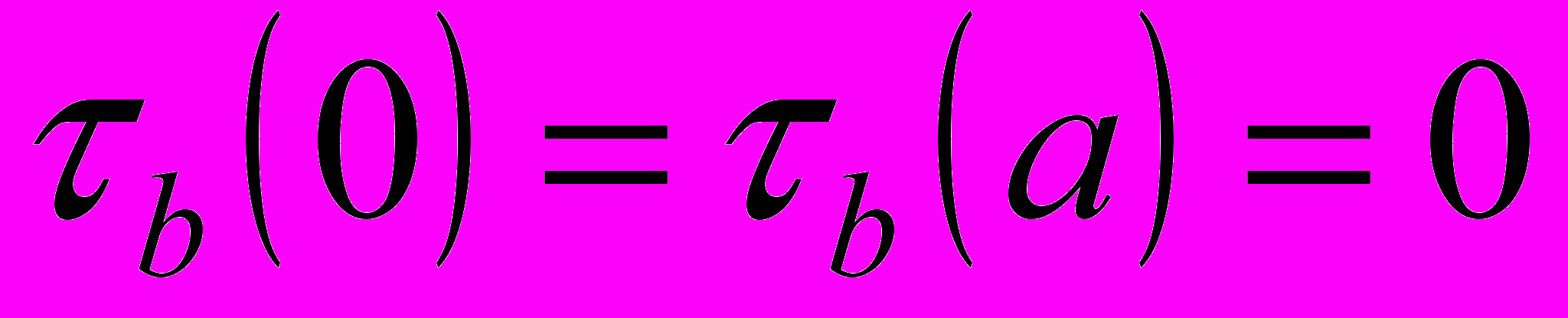, 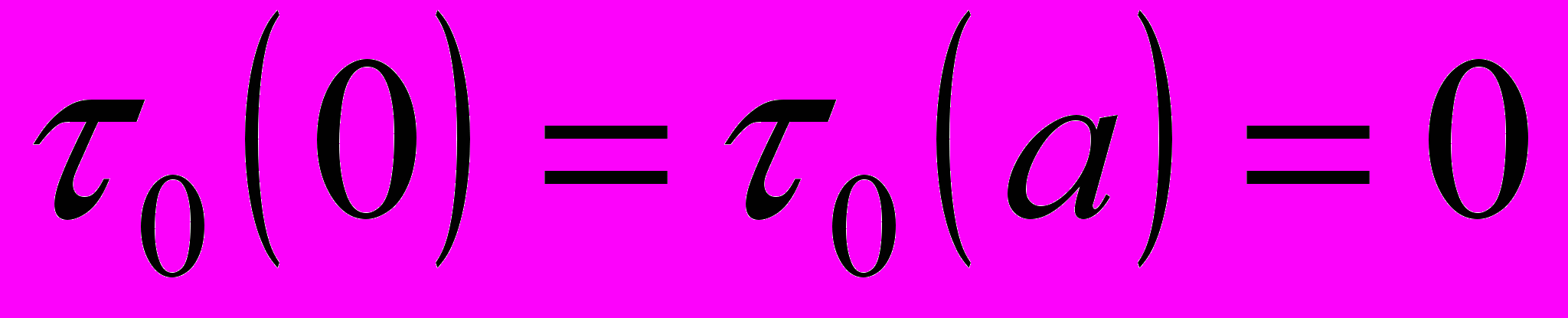то функция

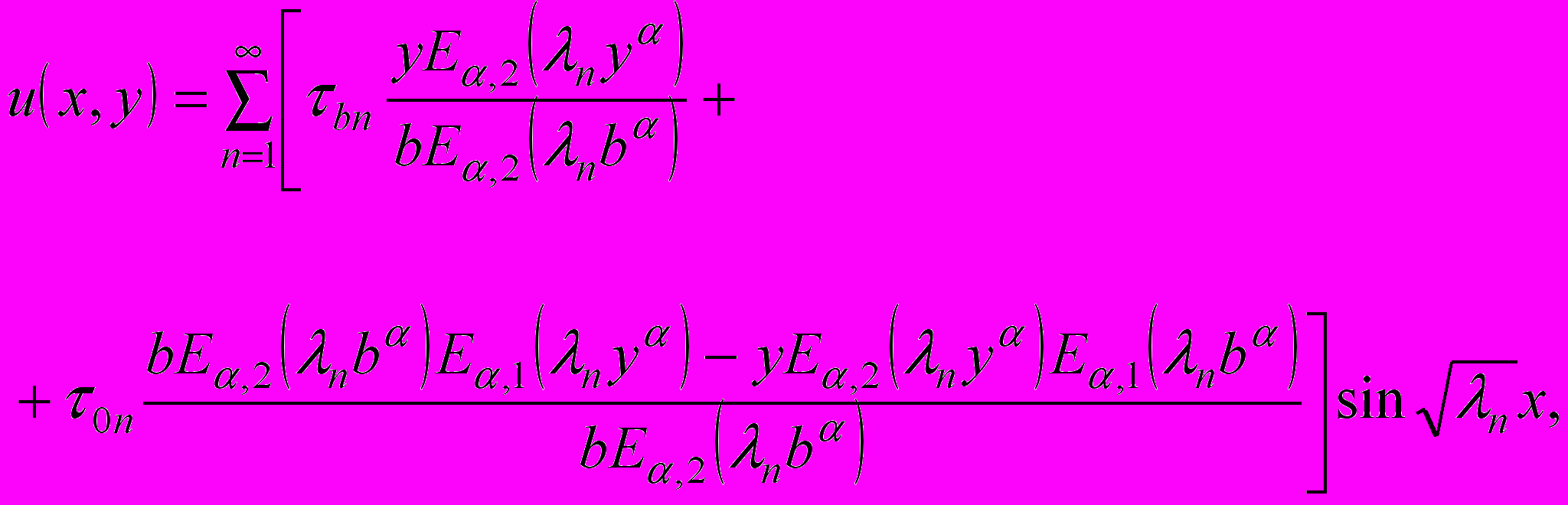(4)

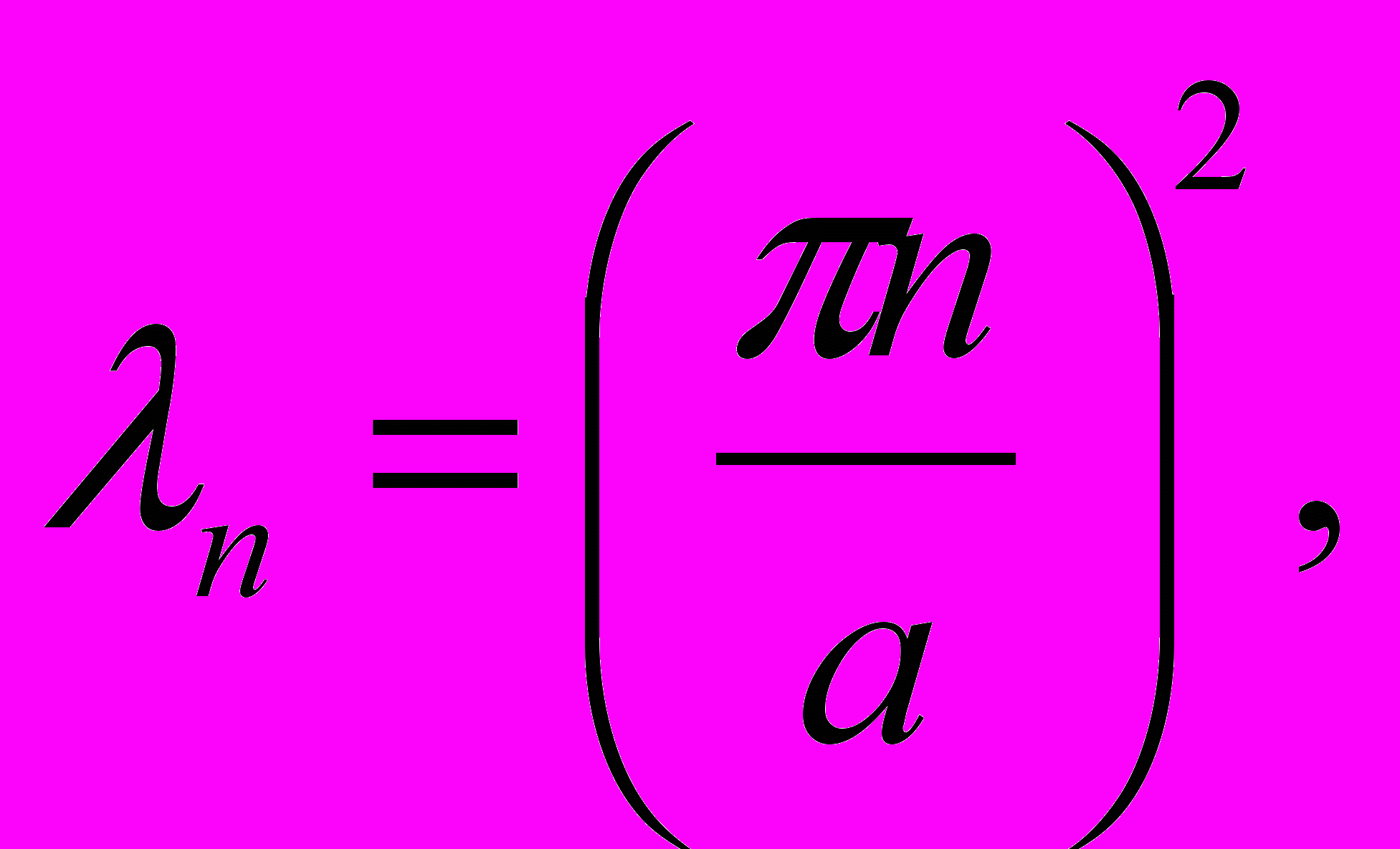
есть решение задачи (1)-(3), где 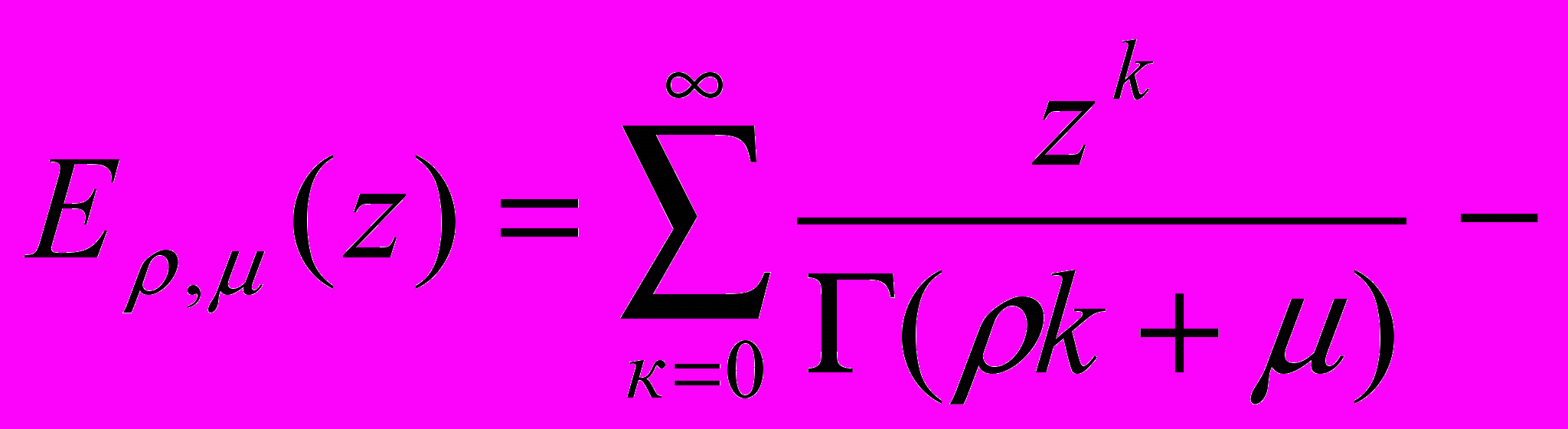функция типа Миттаг – Леффлера.

Теорема 2. Задача (1) – (3) имеет не более одного решения .


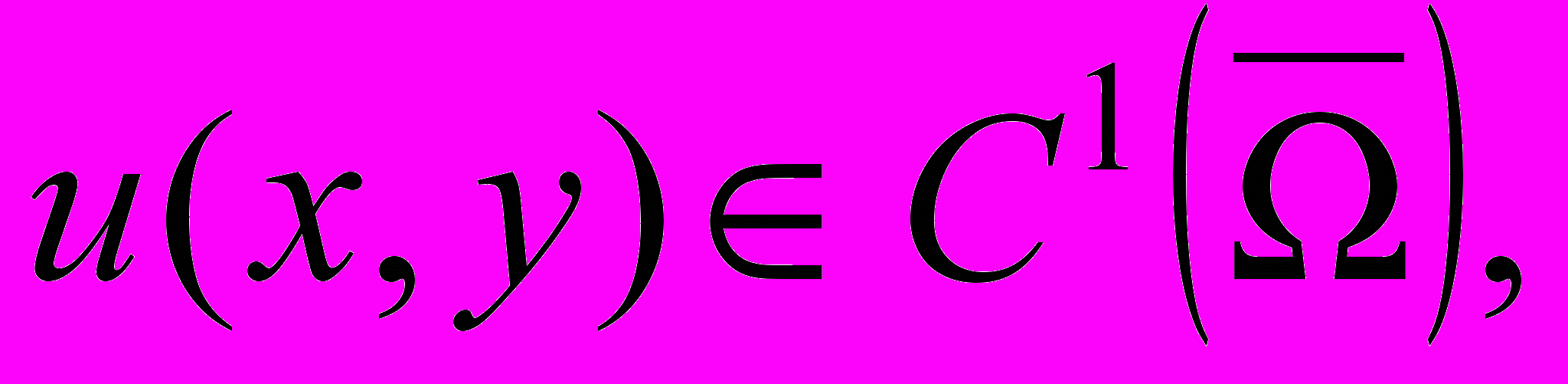
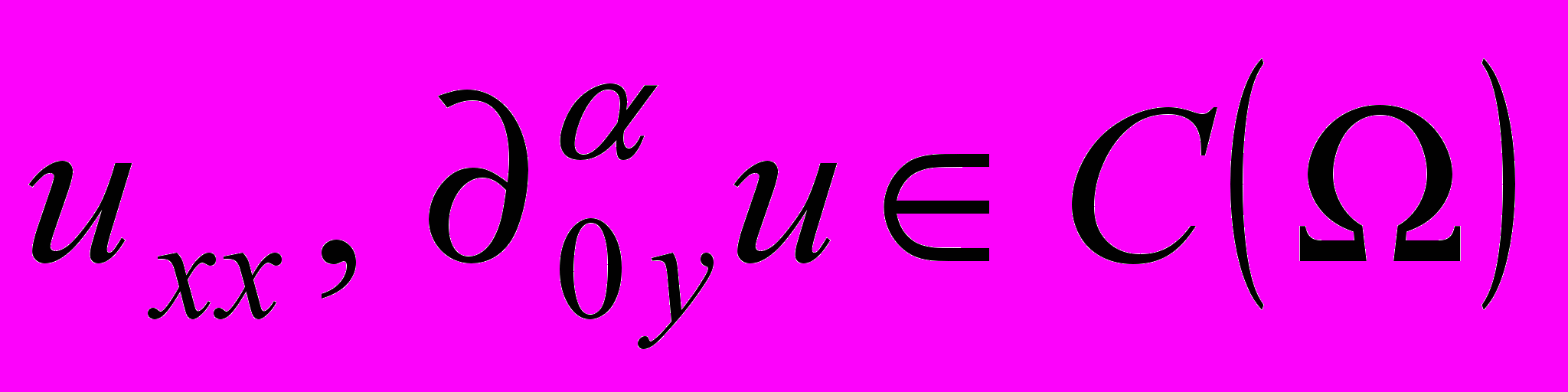Список литературы.

1. Нахушев А.М. Дробное исчисление и его применение. М.: Физматлит, 2003. -272,с.
   
2. Нахушев А.М. О математических и информационных технологиях моделирования и управления региональным развитием //Доклады Адыгской (Черкесской) Международной академии наук. 2007. Т 9, №1. С. 128-137
   
3. Лопушанська Г.П. Основнi граничнi задачi для одного piвняння в дробних похiдних // Укр. мат. журн. 1999. Т. 51, № 1. С. 48-59.
   
4. Еремин А.С. Краевые задачи для дифференциального уравнения, содержащего оператор дробного дифференцирования // Международный Российско-Казахский симпозиум ''Уравнения смешанного типа и родственные проблемы анализа и информатики" и Школы молодых ученых "Нелокальные краевые задачи и проблемы современного анализа и информатики". Материалы, Нальчик-Эльбрус. 2004. С. 73-75.
   
5. Нахушев А.М. Критерий единственности задачи Дирихле для уравнения смешанного типа в цилиндрической области // Дифференц. уравнения. 1970. Т 6. №1.
   
6. Владимиров В.С. Уравнения математической физики. М., 1971, 512 с.