Рабочая программа дисциплины уравнения в конечных разностях направление подготовки

Вид материала

Рабочая программа

Содержание 2. Место дисциплины в структуре ООП бакалавриата 3 Компетенции обучающегося, формируемые в результате освоения дисциплины (модуля) Уравнения в конечных разностях Знать: классификацию уравнений в конечных разностях, методы и способы их решения, Уметь 4. Структура и содержание дисциплины «Уравнения в конечных разностях» Формы текущего контроля успеваемости 5. Образовательные технологии 7. Учебно-методическое и информационное обеспечение дисциплины 8. Материально-техническое обеспечение дисциплины

Подобный материал:

• Рабочая учебная программа дисциплины Уравнения математической физики Направление подготовки, 224.86kb.
• Рабочая программа дисциплины «теоретические основы теплотехники» Направление подготовки, 554.69kb.
• Рабочая программа дисциплины «Техническая термодинамитка» Направление подготовки, 804.99kb.
• Рабочая программа дисциплины Физика, ен. Ф. 03 направление подготовки, 491.56kb.
• Рабочая программа дисциплины «Компьютерная диагностика» Направление подготовки, 209.63kb.
• Рабочая программа дисциплины технические измерения и приборы Направление подготовки, 496.12kb.
• Рабочая программа дисциплины «Основы технологии машиностроения» Направление подготовки, 365.59kb.
• Рабочая программа дисциплины «Интегрированные системы проектирования и управления», 208.14kb.
• Рабочая программа дисциплины «Вычислительные машины, системы и сети» Направление подготовки, 231.13kb.
• Рабочая программа учебной дисциплины «психология» Направление подготовки, 808.24kb.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Томский государственный университет

Факультет прикладной математики и кибернетики


Декан ФПМК

___________________ А.М.Горцев

"_____"__________________2011 г.


РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ

УРАВНЕНИЯ В КОНЕЧНЫХ РАЗНОСТЯХ


Направление подготовки

010400 – Прикладная математика и информатика


Квалификация выпускника

Бакалавр


Форма обучения

очная


Томск

2011

1. Цели освоения дисциплины:

Целями освоения дисциплины «Уравнения в конечных разностях» являются изучение уравнений в конечных разностях, которые широко используются для анализа марковских моделей и преобразования Лапласа-Стилтьеса, применяемое при анализе временных характеристик систем обслуживания.


2. Место дисциплины в структуре ООП бакалавриата:

Данная дисциплина входит в вариативную часть профессионального цикла Б.3. дисциплин Федерального государственного образовательного стандарта высшего профессионального образования (ФГОС ВПО) по направлению «Прикладная математика и информатика» (бакалавриат). Изучается студентами в 4 семестре.

Здесь изучается специфический математический аппарат, который обычно не излагается в курсах математического анализа и дифференциальных уравнений. К числу специфических уравнений, которые часто встречаются в теории массового обслуживания, относятся уравнения в конечных разностях. Рассматриваются линейные однородные и неоднородные уравнения с постоянными коэффициентами, решение которых проводится методами неопределенных коэффициентов, производящих функций, вариации произвольных постоянных, уравнения с переменными коэффициентами и системы уравнений. Изучаются основные свойства преобразования Лапласа-Стилтьеса.

Для изучения данного модуля обучающемуся необходимы знания и умения в следующих областях: математический анализ и линейная алгебра, дифференциальные уравнения, теория вероятностей и математическая статистика, теория случайных процессов.

Данная дисциплина будет необходима для изучения приложений математических методов, в частности, моделей и методов теории случайных процессов и теории массового обслуживания.


3 Компетенции обучающегося, формируемые в результате освоения дисциплины (модуля) Уравнения в конечных разностях:

ОК-1: способность владеть культурой мышления, умение аргументировано и ясно строить устную и письменную речь;

ОК-15: способность работы с информацией из различных источников, включая сетевые ресурсы сети Интернет, для решения профессиональных и социальных задач;

ПК-1: способность демонстрации общенаучных базовых знаний естественных наук, математики и информатики, понимание основных фактов, концепций, принципов теорий, связанных с прикладной математикой и информатикой;

ПК-2: способность приобретать новые научные и профессиональные знания, используя современные образовательные и информационные технологии;

ПК-6: способность осуществлять целенаправленный поиск информации о новейших научных и технологических достижениях в сети Интернет и из других источников;

В результате освоения дисциплины обучающийся должен:

Знать: классификацию уравнений в конечных разностях, методы и способы их решения,

Уметь: определять вид частного решения неоднородного уравнения в конечных разностях, вид общего решения уравнения

Владеть: методами решения уравнений в конечных разностях.

4. Структура и содержание дисциплины «Уравнения в конечных разностях»:

Общая трудоемкость дисциплины составляет 2,2 зачетные единицы 79 часов.

№ п/п	Раздел Дисциплины	Семестр	Неделя семестра	Виды учебной работы, включая самостоятельную работу студентов и трудоемкость (в часах)		Формы текущего контроля успеваемости (по неделям семестра) Форма промежуточной аттестации (по семестрам)
				Лекции	СРС
1	Дифференциальные уравнения, классификация	4	1	2	2
2	Уравнения в конечных разностях – общие замечания	4	2	2	2
3	Линейные однородные уравнения в конечных разностях	4	3-4	4	2
4	Метод неопределенных коэффициентов	4	5	2	2	Контрольная работа, коллоквиум
5	Неоднородные уравнения в конечных разностях	4	6-7	4	2
6	Метод производящих функций	4	8-9	4	1	Контрольная работа, коллоквиум
7	Метод вариации произвольных постоянных	4	10-11	4	1
8	Задача о разорении игрока	4	12	2	2
9	Линейные уравнения конечных с переменными коэффициентами	4	13	2	2
10	Системы уравнений в конечных разностях	4	14	2	2	Контрольная работа, коллоквиум
11	Преобразование Лапласа-Стилтьеса	4	15	2	2	Зачет
	Итого			30	20	29

5. Образовательные технологии

В качестве образовательной технологии выбрана традиционная – лекционно-семинарская система обучения, которая является наиболее информационноемкой. Она пригодна для решения таких задач как передача большого объема информации, развития памяти, внимания, некоторых логических умений обучающихся (выделять главное и существенное, структурировать учебный материал, подбирать доказательство). Составляющие технологии:

• поточно-групповая организация занятий;
  
• еженедельная передача информации небольшими порциями;
  
• постановка преподавателем четких целей обучения;
  
• фронтальная и индивидуальная работа преподавателя со студентами;
  
• индивидуальная работа студентов с учебной литературой;
  
• фрагментарная проверка выполнения самостоятельной работы студентов;
  

Условием эффективного усвоения содержания курса является обязательное сочетание теоретических занятий с практическими, на которых отрабатываются выделенные общие умения, входящие в них знания.

Предусмотрено использование в учебном процессе активных форм проведения занятий (семинары в диалоговом режиме, дискуссии, разработка конкретных ситуаций, групповые дискуссии, результаты работы студенческих исследовательских групп). В рамках учебных курсов предусмотрены встречи с преподавателями российских и зарубежных вузов, участие бакалавров во всероссийских и международных конференциях. Одной из основных активных форм обучения профессиональным компетенциям является семинар, продолжающийся на регулярной основе, к работе которого привлекаются ведущие исследователи и преподаватели.

6. Учебно-методическое обеспечение самостоятельной работы студентов. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины:

Вопросы для контроля:

1. Дифференциальные уравнения, классификация
   
2. Уравнения в конечных разностях – общие замечания
   
3. Линейные однородные уравнения в конечных разностях
   
4. Метод неопределенных коэффициентов
   
5. Неоднородные уравнения в конечных разностях
   
6. Метод производящих функций
   
7. Метод вариации произвольных постоянных
   
8. Задача о разорении игрока
   
9. Линейные уравнения в конечных с переменными коэффициентами
   
10. Системы уравнений в конечных разностях
    
11. Преобразование Лапласа-Стилтьеса
    

Самостоятельная работа:

1. Решить уравнение методом неопределенных коэффициентов
   
2. Решить уравнение методом неопределенных коэффициентов
   
3. Решить уравнение методом неопределенных коэффициентов
   
4. Решить уравнение методом неопределенных коэффициентов
   
5. Найти общее решение однородных уравнений в конечных разностях
   

1. ,
   
2. ,
   
3. ,
   
4. ,
   
5. ,
   
6. .
   

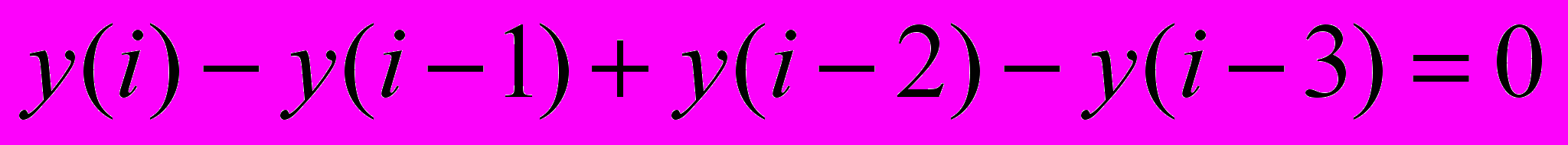6. Найти общее решение неоднородных уравнений в конечных разностях методом неопределенных коэффициентов
   

1. ,
   
2. ,
   
3. ,
   
4. ,
   

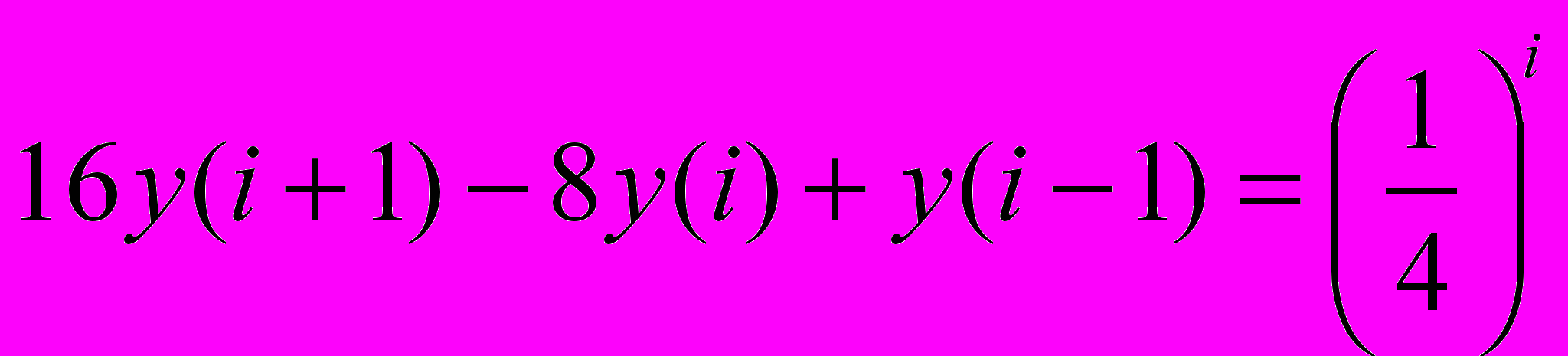7. Решить уравнения в конечных разностях методом неопределенных коэффициентов. Записать частное решение при наличии начальных условий
   

1. , , ,
   
2. , , ,
   
3. , ,.
   

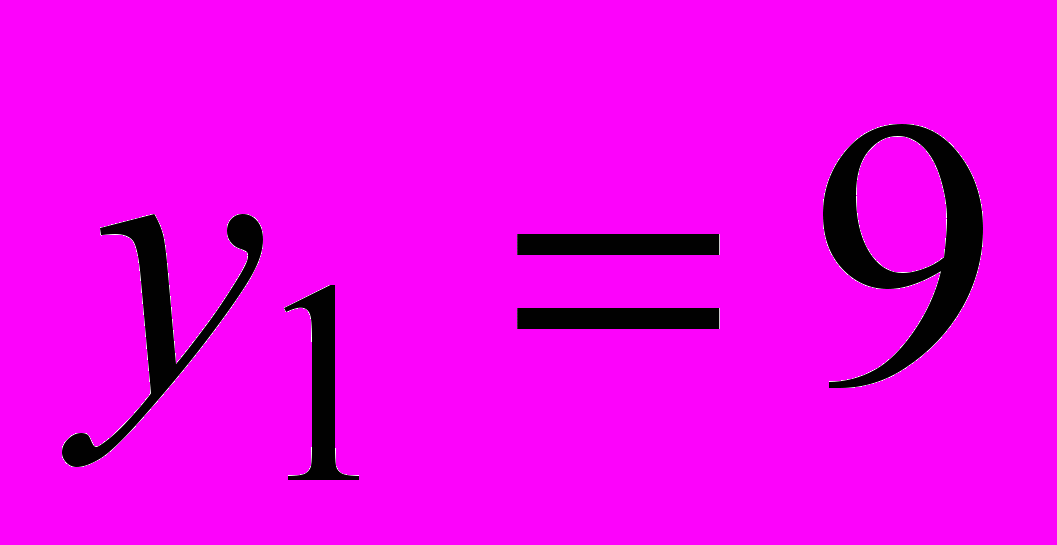8. Решить уравнения в конечных разностях методом производящих функций. Записать частное решение при наличии начальных условий
   

1. , ,,
   
2. ,,,
   

9. , ,,
   

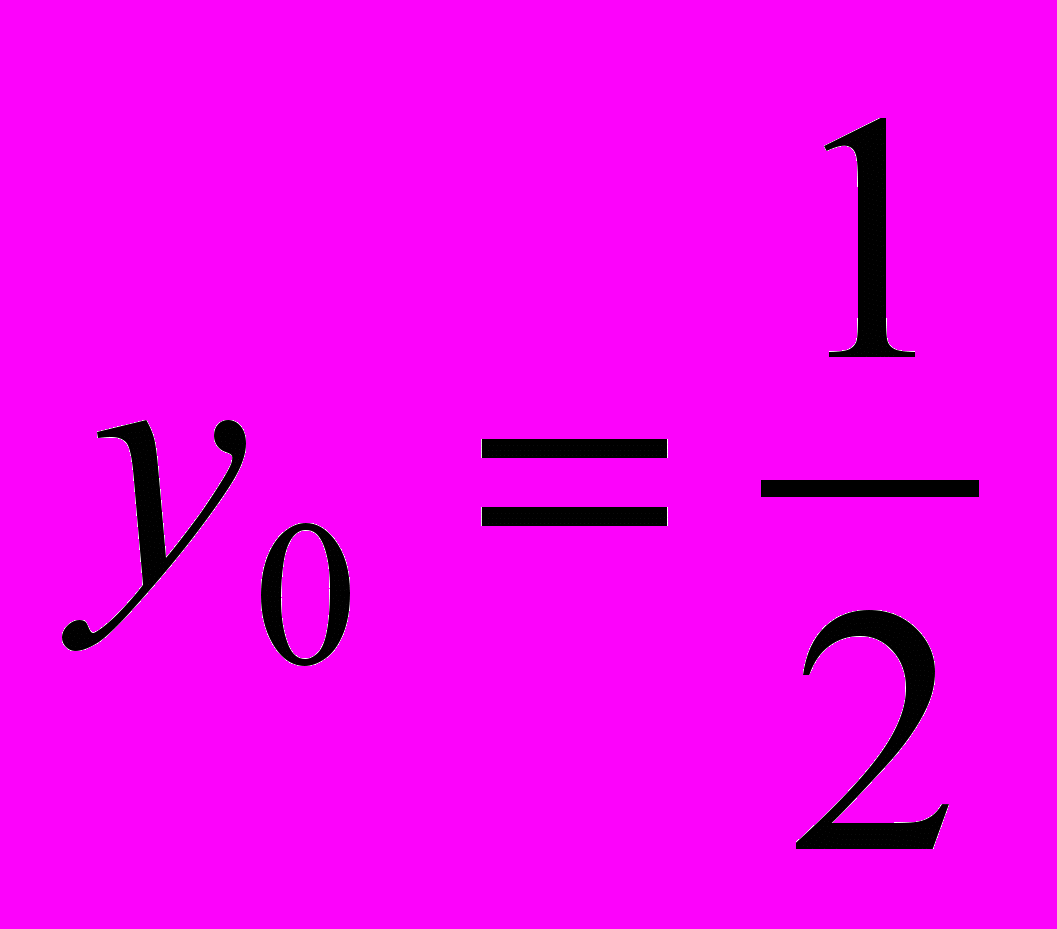Вид учебной работы: лекции. Изучение дисциплины заканчивается зачетом.

7. Учебно-методическое и информационное обеспечение дисциплины:

1. Назаров А.А., Терпугов А.Ф. Теория массового обслуживания: учебное пособие. – Томск: изд. НТЛ, 2004. – 228 с.

2. Гельфонд А.О. Исчисление конечных разностей. – М.: ОНТИ, 1936.


8. Материально-техническое обеспечение дисциплины:

В распоряжении преподавателей и обучающихся имеется основное необходимое материально-техническое оборудование, а именно компьютеры с соответствующим компьютерным обеспечением, Интернет-ресурсы, доступ к полнотекстовым электронным базам, книжный фонд (3,8 млн. экземпляров) Научной библиотеки Томского университета.

Программа составлена в соответствии с требованиями ФГОС ВПО с учетом рекомендаций и ПрООП ВПО по направлению подготовки 010400 – Прикладная математика и информатика.

Автор: к.физ.-мат.н. С.В. Лопухова.

Рецензент: д.техн. н., профессор А.М. Горцев.

Программа одобрена на заседании Ученого Совета ФПМК от «__»___________2011, протокол № ____.