Секция 7 А. Н. Васильев, Д. а тархов

Вид материала

Подобный материал:

СЕКЦИЯ 7

А.Н. Васильев, Д.а. тархов

Санкт-Петербургский государственный политехнический университет

Нейросетевой подход к решению

некоторых неклассических задач

математической физики

Аннотация

В работе показано, что нейронные сети позволяют эффективно находить приближенные решения начально-краевых задач для уравнений в частных производных не только в классической, но и в неклассической постановке. Эти решения обладают свойством устойчивости по отношению к возмущениям входных данных. В качестве примеров рассматриваются нестандартные задачи для уравнения Лапласа и близких к нему уравнений – изучается возмущение уравнения, граничных условий, самой границы, исследуется задача, в которой уравнение задано лишь в части области, где ищется решение, кроме этого решение должно соответствовать некоторым зашумлённым экспериментальным данным.

В данной работе в соответствии с программой, заявленной в статье авторов [1], методология нейронных сетей применяется к численному решению ряда задач математической физики, которые трудно решаются обычными методами.

Рассмотрим краевую задачу

здесь

– некоторый дифференциальный оператор, т.е. алгебраическое выражение, содержащее частные производные от

– оператор, позволяющий задать граничные условия (допустимый оператор),

– граница области

.

Ищем ее решение

в виде нейросетевой аппроксимации

параметры которой (входящие линейно скаляры

и входящие нелинейно векторные параметры

) определяются в процессе обучения нейросети на основе минимизации (в простейшем случае) функционала ошибки в виде

На практике этот функционал заменяется некоторым его дискретным аналогом.

Рассмотрим простейшее уравнение эллиптического типа – уравнение Лапласа

. Оно описывает электростатические поля, стационарные поля температуры и т.п. Условия на границе области, в которой рассматривается поле, как правило, позволяют выделить из бесчисленного множества решений

единственное, отвечающее конкретной физической задаче.

В работе [2] в качестве первых шагов рассматривалось применение нейронных сетей (в основном, RBF типа) к решению краевых задач для уравнения Лапласа в случае плоскости. Основным примером, на котором проверялись нейросетевые методы решения, была задача Дирихле для единичного круга: ищется функция, которая в круге удовлетворяет уравнению Лапласа, а на его границе равна некоторой заданной функции. В качестве следующего шага интересно рассмотреть более сложные задачи.

Во-первых, в любой реальной задаче присутствуют случайные добавки – погрешности измерений, шумы и т.д. Для изучения влияния таких добавок было рассмотрено несколько задач.

Первая такая задача получается заменой уравнения Лапласа уравнением Шредингера со случайным потенциалом

, где

– случайная функция типа белого шума определённой амплитуды

, т.е. каждой точке круга ставится в соответствие независимая случайная величина, распределённая равномерно на промежутке

. Численные эксперименты проводились при

равном 0.01, 0.1 и 1. В первом случае результаты не отличаются от результатов в отсутствие шума, при этом обучение происходит даже несколько быстрее. Для амплитуды

результат тоже оказался достаточно близким. При амплитуде шума

существенные отличия наблюдаются только в точках максимума и минимума решения, а его общий характер не меняется.

Вторая задача получается введением аналогичной случайной добавки в граничное условие: функция

заменяется данными

, где

– равномерный белый шум амплитуды

. Численные эксперименты дали аналогичные результаты, при этом малый шум опять ускорил обучение на начальном этапе.

Третья задача возникает при возмущении границы

: случайная функция вводится в уравнение окружности. Эта постановка задачи достаточно естественна, так как идеальных кривых (в частности, окружностей) в природе нет. Численные эксперименты показали, что для предлагаемого подхода эта задача сложнее, чем две предыдущие, однако при амплитуде добавки 0.01 получаются вполне приемлемые результаты. Сложность задачи вызвана тем, что мы фактически требуем выполнения граничных условий в некоторой области (окрестности границы) – в данном случае в кольце. Возможно, для этой задачи более эффективным окажется применение многослойного персептрона или некоторой гибридной сети.

В четвертой задаче рассматривается случай составной области

, в подобласти

которой выполняется уравнение

– малая случайная функция (нами рассматривался белый шум фиксированной амплитуды

), а в дополнении

– уравнение

, на границе

выполняется, например, условие Дирихле

на

– естественное условие согласования. Для численных экспериментов в качестве области

, по-прежнему, выбирался единичный круг, а в качестве

– круг радиуса 0.4, центр которого смещён на 0.4 относительно начала координат,

нейросеть – из 150 персептронов.

Рис. 1. График решения

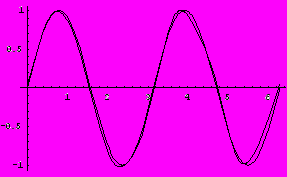
Рис. 2. Удовлетворение краевому условию

Рис. 3. График решения

на сечении

Рис. 4. График значения

на сечении

Во-вторых, возможным усложнением задачи является рассмотрение нелинейных уравнений. Первый естественный шаг в таком направлении – заменить уравнение Лапласа уравнением

, где

– некоторая нелинейная функция. Мы рассматривали два примера таких функций. В первом –

, где вычитание единицы позволяет рассматривать нетривиальное решение при однородном граничном условии. В этой задаче получилась достаточно хорошая сходимость (значительно быстрее, чем в задаче Дирихле для уравнения Лапласа). Во втором –

. Это известное уравнение в теории горения при однородном условии на границе:

при

, –- имеет два решения – одно ограниченное и отрицательное, другое положительное и неограниченное. Процесс обучения достаточно быстро сходится к первому решению. Для получения второго, по-видимому, следует рассмотреть неограниченные базисные функции.

Важное для приложений уравнение Шредингера с кубической нелинейностью рассмотрено в статье [3].

В-третьих, можно рассмотреть более сложные граничные условия. Один из таких вариантов – задание граничного условия не на всей границе, а только на её части. Численное исследование такой задачи, когда граничное условие задано только на полуокружности, привело к интересному результату: на другой половине окружности обученная сеть даёт естественное граничное условие – равенство нулю нормальной производной, ожидать выполнения которого при рассматриваемом подходе, казалось, не было никаких оснований. Другой вариант задания нетрадиционного граничного условия – добавить к условию на границе условие на луче, выходящем из начала координат. Численный эксперимент показал вполне приемлемую точность и сходимость процесса обучения, если не считать окрестность начала координат, в которой возникает естественная особенность. Аналогичный результат получается и в задаче Зарембы, когда на части границы задана функция, а на другой части – нормальная производная – сходимость портится только в точках стыка условий. Следует отметить, что в этой задаче асимметрические RBF-сети [2] показали себя намного эффективней обычных.

В качестве нового примера нестандартной постановки рассмотрим задачу нахождения функции, для которой в некоторой части области известно уравнение, кроме того, известны (например, в результате измерений) её значения в некотором наборе точек. Будем искать

, где

, удовлетворяющую условиям:

– эллиптический оператор.

Авторам неизвестны какие-либо классические подходы к решению этой задачи. Нами предлагается нейросетевая аппроксимация решения с помощью RBF-сети из гауссовых функций

где

– евклидова норма в

вместо гауссианов возможен выбор и других функций (Коши, мультиквадратиксы и т.п.). Другой вариант – аппроксимирующая нейросеть из однослойных персептронов

где нелинейная функция

задается как

, возможны и другие формы активационных функций

, например,

. Параметры сети – коэффициенты

– находятся из условия минимизации функционала ошибки

дискретный аналог которого имеет вид

здесь

– набор тестовых точек в

Для расчетов выбирался двумерный оператор Лапласа

область

. Пусть заменяющие краевые условия «измеряемые» данные

известны с ошибкой, которая является случайной величиной, равномерно распределенной на отрезке

. В качестве тестовой была взята функция

. Получился удивительный результат. Выберем

. Если в виде исходных требований к решению помимо удовлетворения уравнению Лапласа в полукруге

задать значения решения со случайной ошибкой

в 3 случайных точках в

, а в полукруге

взять решение с такой же ошибкой в 7 случайных точках, то сеть позволяет найти решение с той же ошибкой

. При этом граничные условия никак не задаются!

Рис. 5. График решения

Рис. 6. График

Результаты приведены для гауссовой RBF сети из 30 функций:

. (Применение нейронной сети на персептронах дало существенно более плохие результаты.) Среднеквадратичные ошибки в удовлетворении уравнению Лапласа

и тестовому краевому условию

равны соответственно

. График поточечного удовлетворения тестовому краевому условию дан выше.

Рис. 7. График

На последнем рисунке приведены аналогичные результаты для другого значения штрафного параметра:

.

Список литературы

Васильев А.Н., Тархов Д.А. Нейронные сети как новый универсальный подход к численному решению задач математической физики // Нейрокомпьютеры: разработка, применение. М.: Радиотехника. 2004. № 7-8.
Васильев А.Н., Тархов Д.А. Новые подходы на основе RBF – сетей к решению краевых задач для уравнения Лапласа на плоскости // Нейрокомпьютеры: разработка, применение. М.: Радиотехника. 2004. № 7-8.
Васильев А.Н., Тархов Д.А. Нейросетевые подходы к решению краевых задач в многомерных составных областях. Известия ТРТУ (в печати).

УДК 004.032.26(06) Нейронные сети

Blog

Секция 7 А. Н. Васильев, Д. а тархов