Geum.ru

Решение задачи о пористом катализаторе на основе нейросетевого подхода а. Н. Васильев, профессор фмф спбгпу, a n. vasilyev@gmail com Д. А. Тархов

Вид материалаРешение
Подобный материал:
РЕШЕНИЕ ЗАДАЧИ

О ПОРИСТОМ КАТАЛИЗАТОРЕ

НА ОСНОВЕ НЕЙРОСЕТЕВОГО ПОДХОДА


А.Н.Васильев, профессор ФМФ СПбГПУ, a.n.vasilyev@gmail.com

Д.А.Тархов, профессор ФМФ СПбГПУ, dtarkhov@gmail.com

Анализ баланса тепла и массы в грануле пористого катализатора при каталитической химической реакции приводит к следующей задаче [1]:

требуется найти решение нелинейного обыкновенного дифференциального уравнения



удовлетворяющее краевым условиям



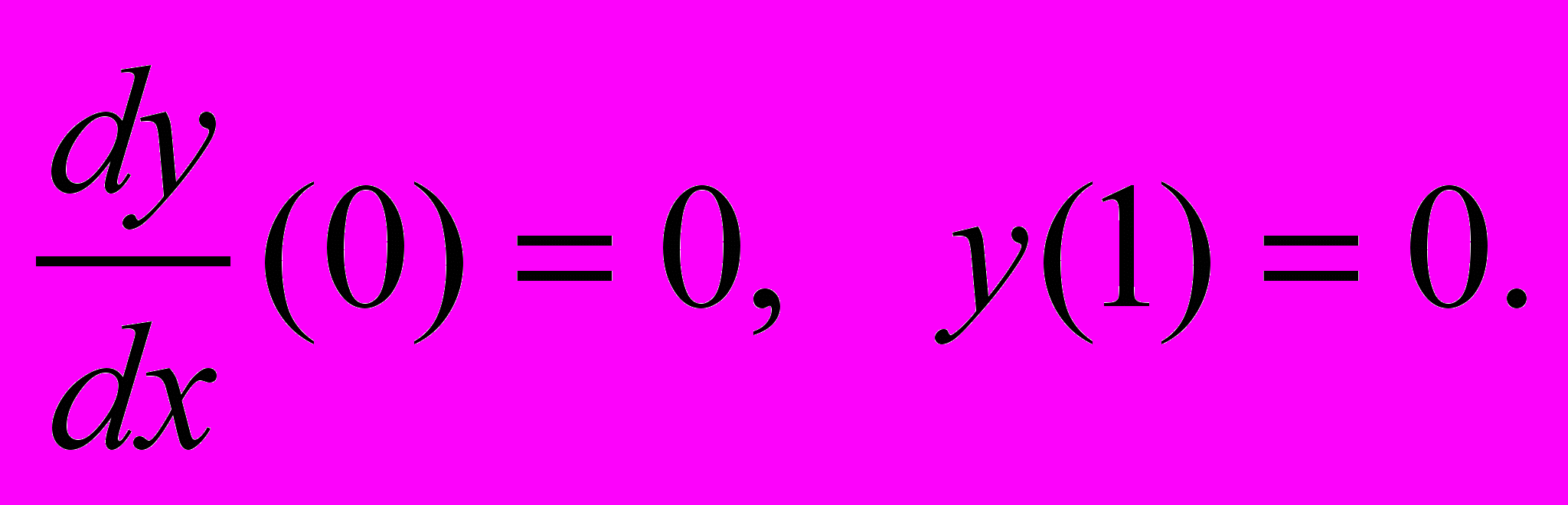
В работе [2] из материалов VI Международной конференции NPNJ'2006 приведены два метода численного решения дискретного аналога поставленной задачи – ее разностной аппроксимации: метод Лаэя [3] и метод дискретного продолжения по наилучшему параметру [4]. Результаты вычислений по этим оригинальным методам, к сожалению, не приводятся, но утверждается, что они совпадают с результатами, полученными методом интегральных уравнений, которые приведены в известной монографии [5].

Применим к этой нелинейной задаче развиваемый авторами нейросетевой подход к построению устойчивых приближенных моделей сложных систем (см., например, работу [6], [7] и другие публикации авторов [8-17]).

Поясним суть этого подхода на простейшей (вообще говоря, нелинейной) краевой задаче

(1)

здесь 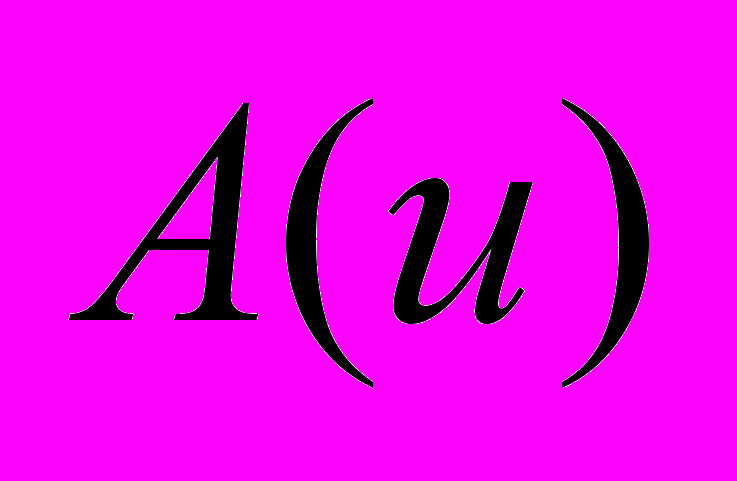– некоторый дифференциальный оператор, т.е. алгебраическое выражение, содержащее обыкновенные или частные производные от неизвестной функции , – оператор, позволяющий задать граничные условия, – граница области .

Ищем приближённое решение задачи (1) в виде выхода искусственной нейронной сети заданной архитектуры веса которой – линейно входящие параметры и нелинейно входящие параметры – определяются в процессе поэтапного обучения сети на основе минимизации функционала ошибки вида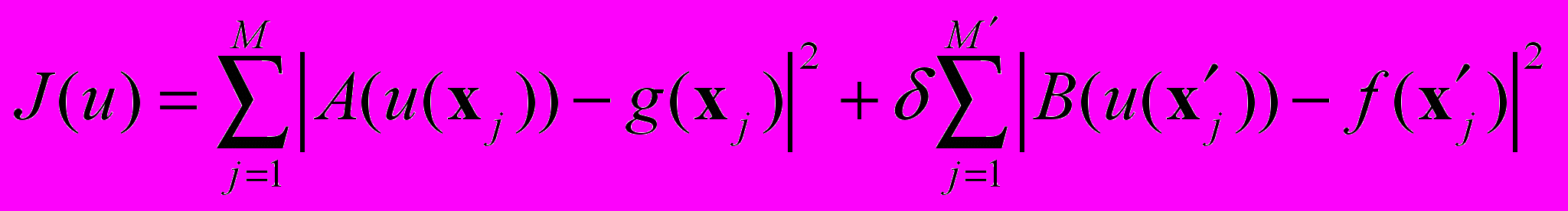

. (2)

Здесь – периодически перегенерируемые пробные точки в области , – пробные точки на её границе ; штрафной параметр.

В нашем случае 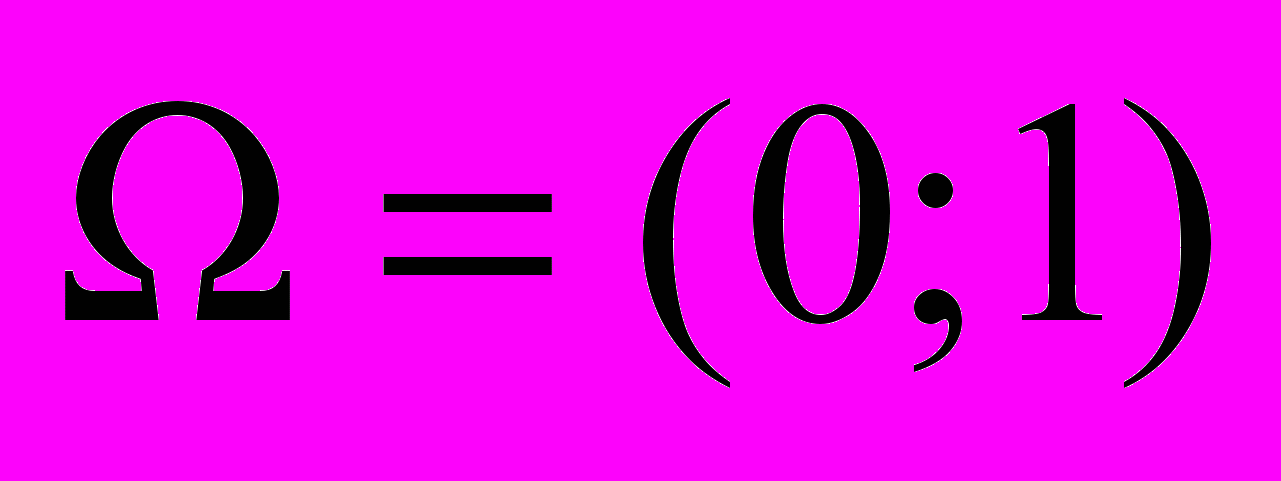, , в качестве базисных нейроэлементов, к примеру, могут быть выбраны гауссианы 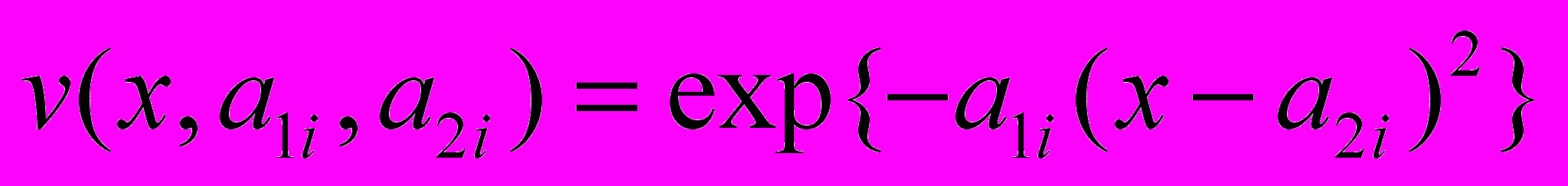, здесь 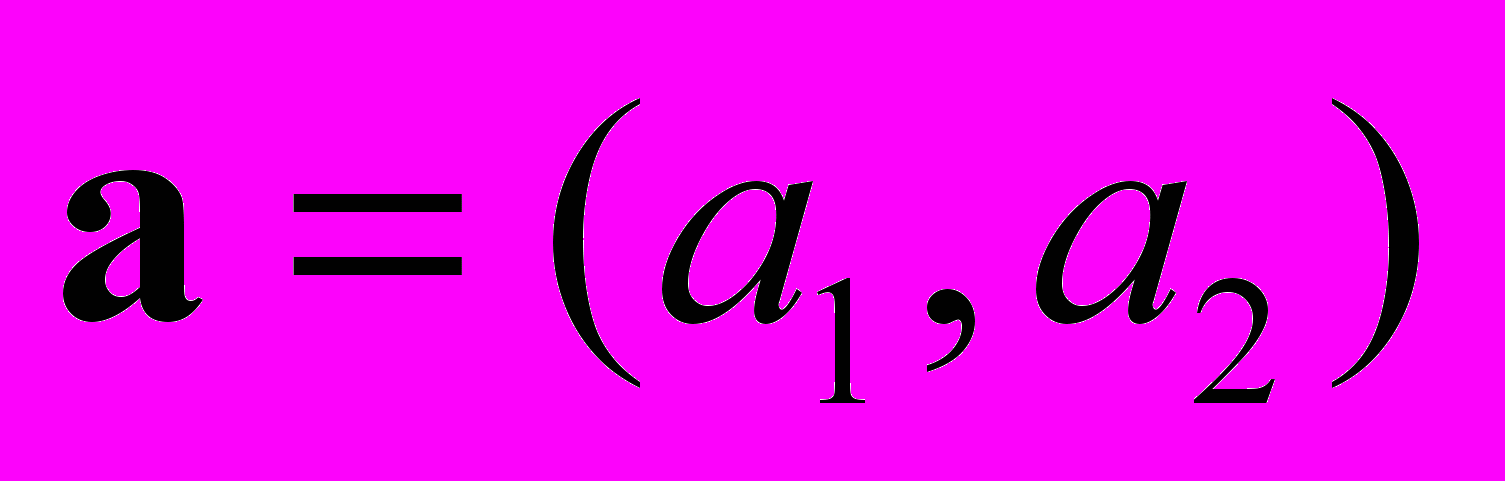, , а для функционала ошибки используется выражение вида



В качестве метода глобальной минимизации для настройки параметров приближенного нейросетевого решения выбирался модифицированный метод многогранника [7]. С целью сравнения результатов с результатами, полученными в [5], вычисления проводились для тех же значений параметров: ,,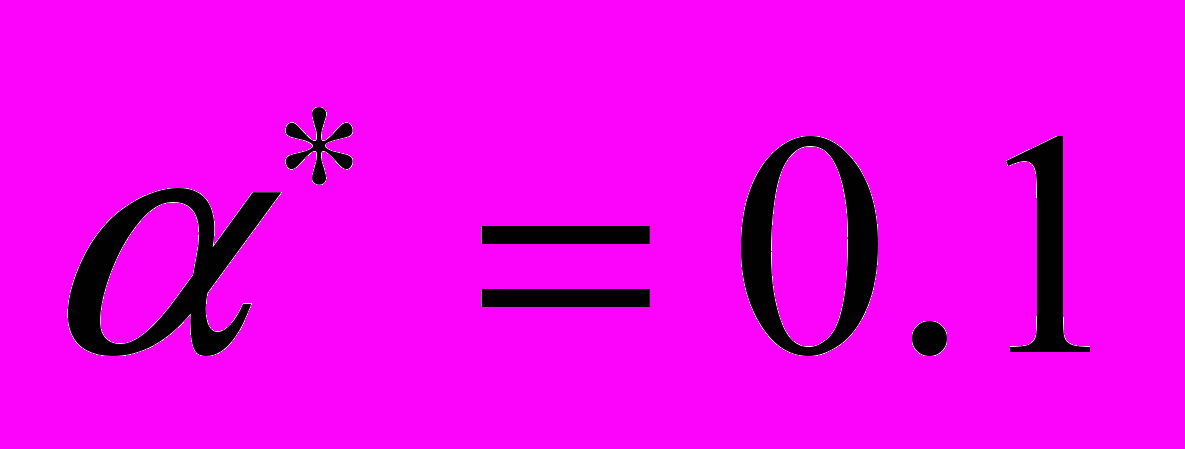


Уже для 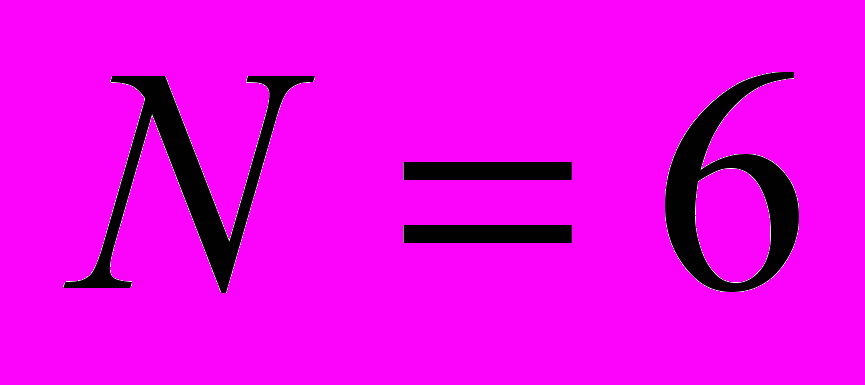удалось построить приближенное нейросетевое решение задачи со среднеквадратичной ошибкой порядка (относительной ошибкой, не превосходящей 0.08%), устойчивое по отношению к возмущениям ее параметров, при этом решение представлено в аналитической форме, его значения в контрольных точках совпали с данными, приведенными в монографии [5].



Рис. 1. График нейросетевого решения задачи для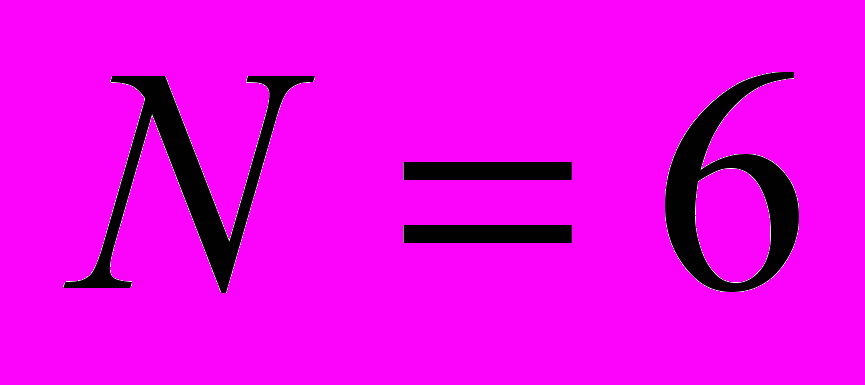


Ещё более интересной является задача построения нейронной сети, дающей решение задачи не при фиксированных значениях параметра, а значениях из некоторого интервала. При этом данный параметр надо подать на вход сети наряду с переменной . В качестве такого параметра можно было бы выбрать , так как зависимость от него наиболее интересна с точки зрения приложений. Однако более заманчиво ввести в рассмотрение все три параметра: , и .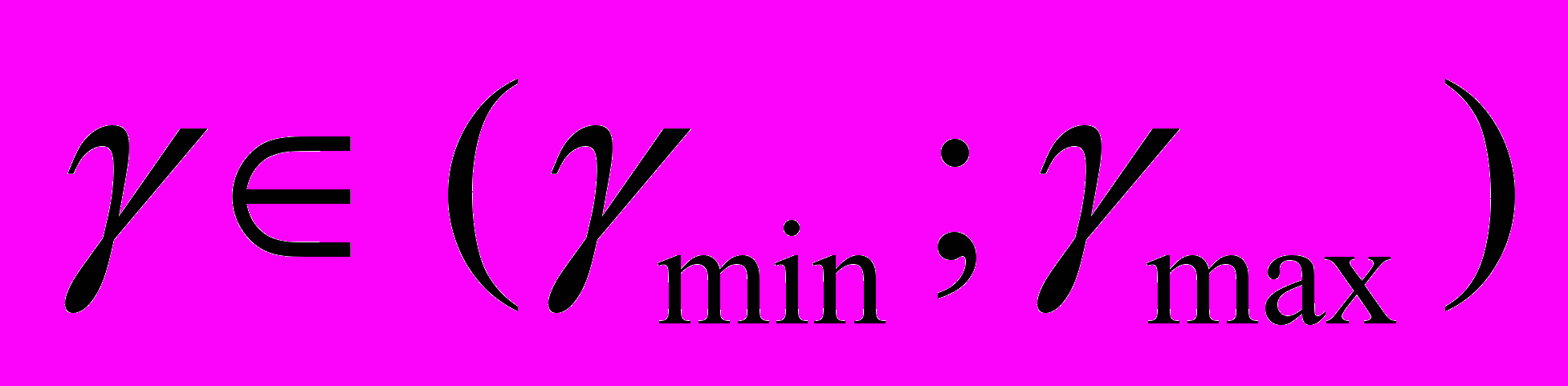

При этом в качестве базисных функций можно было бы взять гауссианы

,


но более эффективным оказалось использование гетерогенной нейронной сети с базисными нейроэлементами вида

.


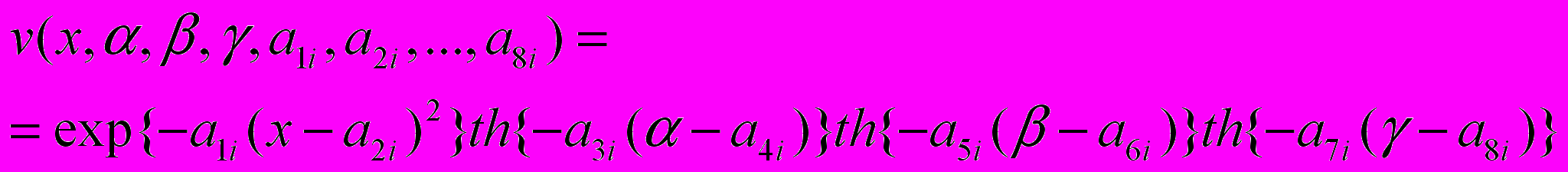Минимизируемый функционал ошибки зададим в виде –



Вычисления проводились для следующих интервалов изменения параметров . Оптимальные значения весов приближенного нейросетевого решения подбирались на основе минимизации функционала как с помощью модифицированного метода многогранника, так и с помощью варианта метода плотного облака, который в данном случае оказался более эффективным. 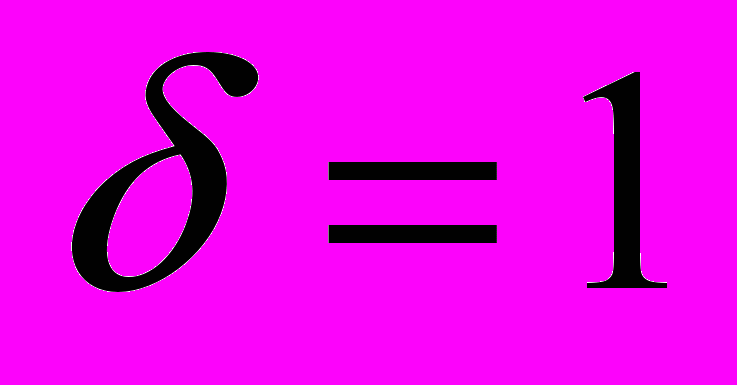Приведем результаты вычислений для сети из нейроэлементов при следующих значениях параметров: размер облака , штрафной множитель , число тестовых точек 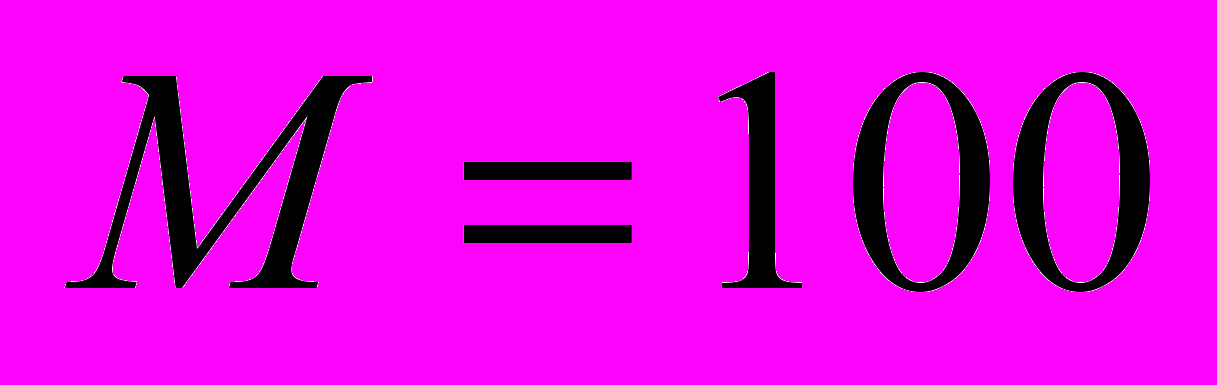. Полученное приближенное решение задачи дается нейронной сетью в аналитической форме для указанной области изменения параметров . Его значения в контрольных точках отличаются от приведенных в монографии [5] данных менее чем на 2%.

На приведенных ниже рисунках указаны графики нейросетевого решения для контрольной точки и на соответствующих сечениях:




Рис. 2. График нейросетевого решения задачидля




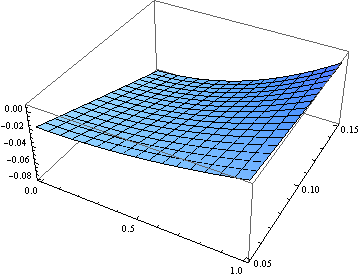
Рис. 3. График нейрорешения задачи ,




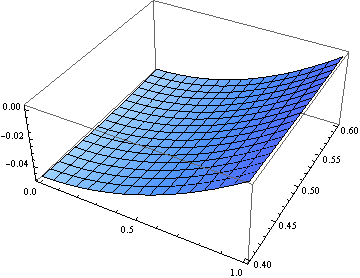
Рис. 4. График нейрорешения задачи ,




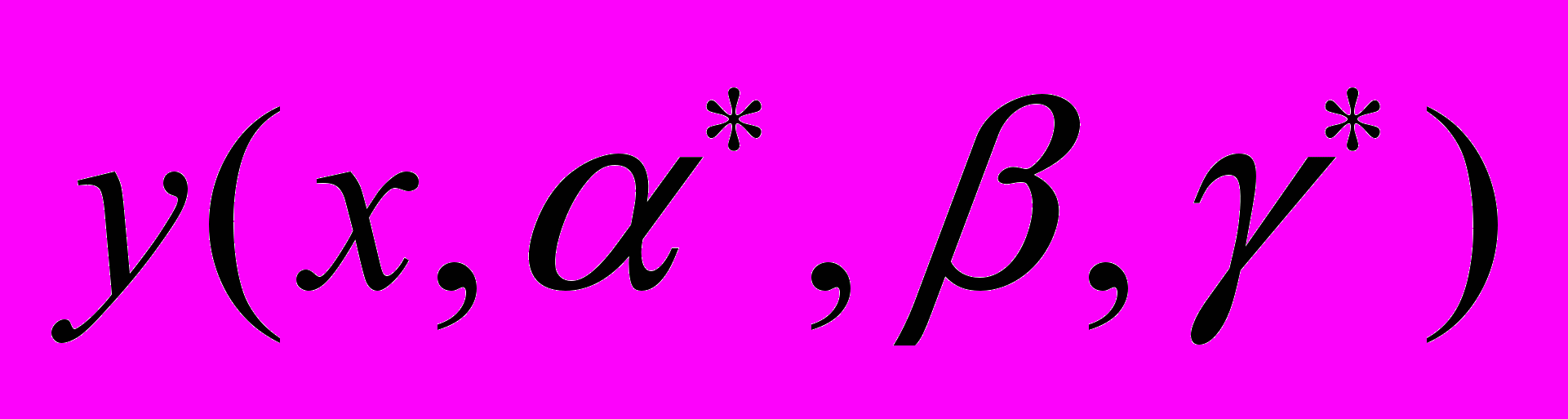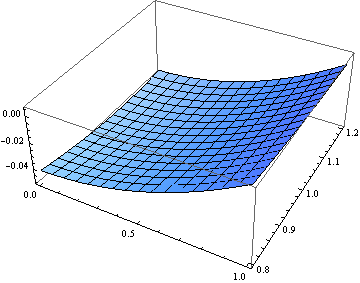
Рис. 5. График нейрорешения задачи ,


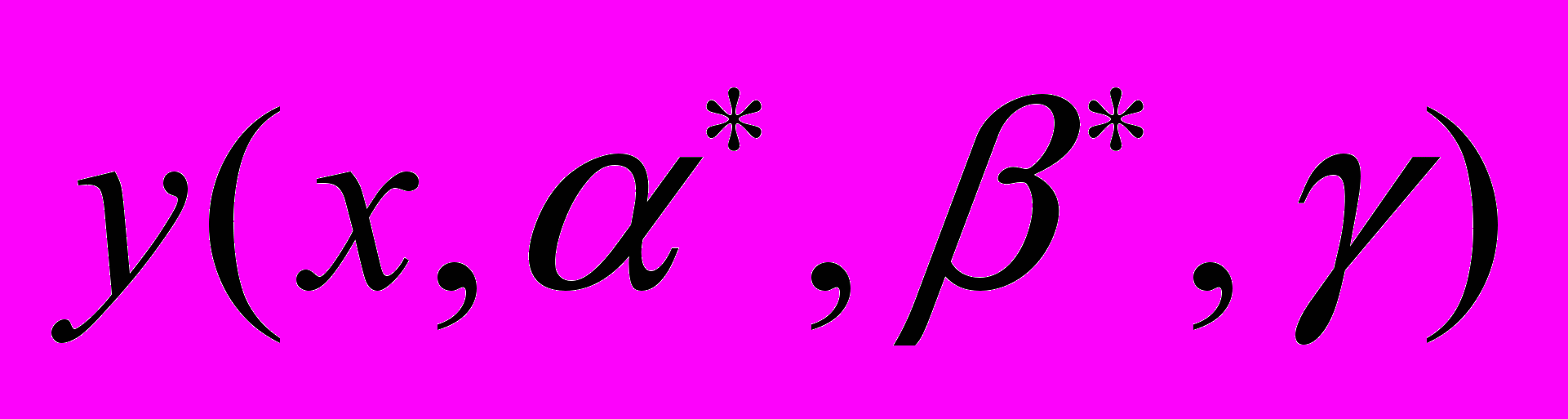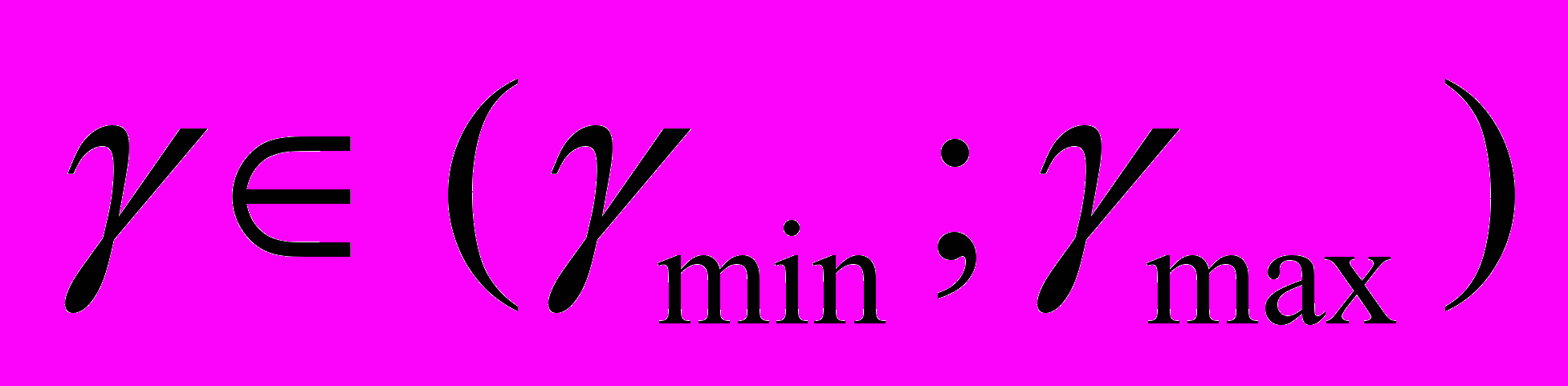
Наряду с этим результат нейрокомпьютинга сравнивался с решением, полученным численными методами, реализованными в ядре среды Mathematica 6, – получилось очень хорошее совпадение. Предложенная методика, существенно используя достоинства нейросетевых разложений [6], позволяет работать не только с нелинейными одномерными задачами, она может быть применена в случае кусочных коэффициентов в многомерных задачах со сложной геометрией, при решении серии задач с уточняемой постановкой, при построении регуляризаций решений некорректных задач.

Литература

1. Дмитриев С.С., Кузнецов Е.Б. Перенос тепла и массы в пористом катализаторе// Материалы VI Международной конференции по неравновесным процессам в соплах и струях – NPNJ-2006, СПб. – М.: Вузовская книга, 2006. – С.159-160.

2. Kubicek M., Hlavacek V. Solution of nonlinear boundary value problems. Part VIII// Chem. Eng. Sci. 1974. V. 29. P.1695-1699.

3. Lahae M.E. Solution of systems of transcendental equations// Acad. R. Belg. Bull.Cl. Sci. 5. 1948. P. 805-822.

4. Кузнецов Е.Б. Наилучшая параметризация при построении кривой итерационным методом// Докл. РАН. 2004. Т. 396, № 6. С. 746-748.

5. На Ц. Вычислительные методы решения прикладных граничных задач. – М.: Мир, 1982, 296 с.

6. Васильев А.Н. Построение приближенных математических моделей распределенных систем на основе нейросетевой методологии// «Нейрокомпьютеры»: разработка, применение. – М.: Радиотехника, 2007. – №9. – С.103-116.

7. Тархов Д.А. Нейронные сети: модели и алгоритмы. Кн.18. – М.: Радиотехника, 2005. – 256 с.

8. Vasilyev A.N., Tarkhov D.A. New neural network technique to the numerical solution of mathematical physics problems. I: Simple problems// Optical Memory and Neural Networks (Information Optics), Allerton Press, Inc. –2005. – Vol. 14, No. 1. – pp. 59-72.

9. Vasilyev A.N., Tarkhov D.A. New neural network technique to the numerical solution of mathematical physics problems. II: Complicated and nonstandard problems// Optical Memory and Neural Networks (Information Optics), Allerton Press, Inc. – 2005. – Vol. 14, No. 2. – pp. 97-122.

10. Васильев А.Н., Тархов Д.А. Нейросетевые подходы к решению краевых задач в многомерных составных областях// Известия ТРТУ. – 2004. – №9. – С.80-89.

11. Васильев А.Н., Тархов Д.А. Применение искусственных нейронных сетей к моделированию многокомпонентных систем со свободной границей// Известия ТРТУ. – 2004. – №9. – С.89-100.

12. Тархов Д.А. Нейронные сети как средство математического моделирования// «Нейрокомпьютеры»: разработка, применение. – 2006. – №2. – С.3-48. 13. Васильев А.Н., Тархов Д.А. Нейросетевой подход к расчету квантовых точек// «Нейрокомпьютеры»: разработка, применение. – 2007. – №6. – С.87-95.

14. Васильев А.Н., Тархов Д.А. Расчет теплообмена в системе «сосуды–ткани» на основе нейронных сетей// «Нейрокомпьютеры»: разработка, применение. – 2006. – №7. – С.48-53.

15. Васильев А.Н. Сравнительный анализ традиционного и нейросетевого подходов к построению приближенной модели калибратора переменного давления// «Нейрокомпьютеры»: разработка, применение. – М.: Радиотехника, 2007. – №9. – С.14-23.

16. Васильев А.Н., Тархов Д.А. Эволюционные алгоритмы решения краевых задач в областях, допускающих декомпозицию (NPNJ-2006)// Математическое моделирование. – 2007. – Том 19, №12. – С.52-62.

17. Васильев А.Н., Тархов Д.А. Построение приближённых нейросетевых моделей по разнородным данным// Математическое моделирование. – 2007. – Том 19, №12. – С.43-51.