Задачи стратегического управления. Моделирование задач оперативного управления. Модели управления проектами. Задачи стратегического управления

Вид материала

Лекция

Содержание Задачи стратегического управления Моделирование задач оперативного управления. Сетевые модели Модели управления проектами Разновидности сетевых графиков. Расчет сетевой модели

Подобный материал:

• Стратегический менеджмент, 380.95kb.
• Магистерская программа «Стратегический менеджмент в промышленности» Аннотация программы, 202.22kb.
• Темы дипломных работ Проблемы стратегического управления производством в условиях российского, 56.04kb.
• Тематический план. Блок Предпосылки стратегического управления в бизнесе. Основные, 1025.57kb.
• Программа учебной дисциплины «Теория и практика стратегического управления» для магистров, 737.23kb.
• Задачи менеджмента при формировании стратегий интегрированной логистической поддержки, 86.11kb.
• Кафедра Стратегического планирования и методологии управления, 56.55kb.
• Рабочая программа дисциплины «Организация работы отдела рекламы и связей с общественностью», 134.42kb.
• Катаргин Дисциплина "Сетевое моделирование и задачи управления запасами", 9.32kb.
• Элементы и факторы стратегического управления предприятием Введение, 23.86kb.

Лекция 6

Модели организационного управления.

Задачи стратегического управления. Моделирование задач оперативного управления. Модели управления проектами.

Задачи стратегического управления.

Лицам, занимающим руководящие посты, постоянно приходится принимать управленческие решения стратегического и тактического характера. Повышение качества организационного управления можно достичь за счет улучшения качества управляющих решений, координации, контроля, и также за счет создания более совершенных систем. Применение математического моделирования позволяет резко повышать качество управляющих решений. Для построения математической модели необходимо провести качественный и количественный анализ задачи организационного управления. Анализ проводится на основе системного подхода и предполагает выявление всех существенных элементов задачи и взаимосвязей. Проведение системного анализа осуществляется группой специалистов: математиков, экономистов, психологов и т.д.

К моделям математического программирования относят линейные, нелинейные, динамические, целочисленные, имитационные модели.
^

Задачи стратегического управления

Для принятия крупномасштабных плановых решений стратегического характера используются модели линейного программирования (ЛП). Линейное программирование относится к числу наиболее широко распространенных методов, применяемых для решения производственных и коммерческих задач.

Модель ЛП должна содержать целевую функцию и некоторую совокупность ограничений. Физический смысл целевой функции зависит от существа организационной задачи. В задачах производственно-экономического характера целевая функция чаще всего представляет собой прибыль (максимизация) или затраты (минимизация). Ограничения определяют область допустимых значений управляемых переменных, т.е. измеримых величин, значения которых подлежат оптимизации. Выраженные через управляемые переменные целевая функция и ограничения составляют модель организационного управления.

Процесс построения модели ЛП включает следующие этапы:

1. Диагностический этап (качественный анализ). Цель этого этапа - выявление наиболее важных факторов, содержание управляющих решений, критерии оценки эффективности вариантов решений, схема оценки и сравнения критериев.
   
2. Формулировка задачи, включающая следующие шаги:
   
   1. Выделение управляемых переменных (измеримые величины, значения которых подлежат оптимизации.)
      
   2. Построение целевой функции, как функции управляемых переменных
      
   3. Построение системы ограничений, выраженных через управляемые переменные
      
   4. Выбор метода решения
      
3. Проведение анализа на чувствительность решения модели к вариациям параметров модели.
   
4. Внедрение модели
   

Алгоритм составления модели ЛП:

1. Выбор переменных
   
2. Составление целевой функции f(x)
   
3. составление системы ограничений
   
4. определение оптимальных значений каждой переменной 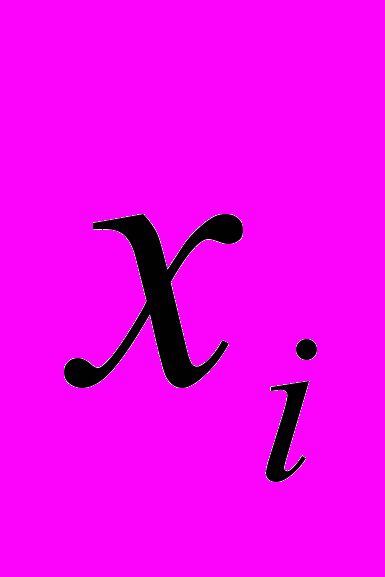(анализ на чувствительность модели).
   

Задача организационного управления формулируется следующим образом: найти такие значения всех 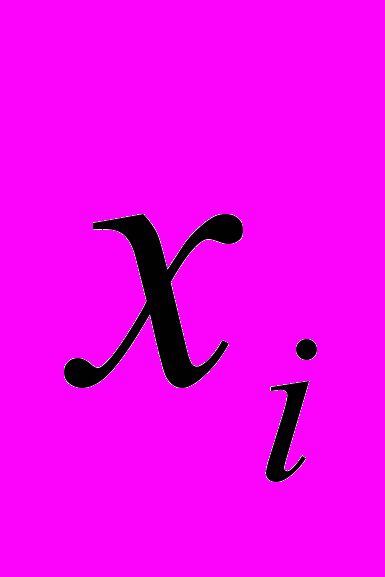, удовлетворяющие ограничениям, которые максимизируют (минимизируют) целевую функцию. Такие значения не обязательно являются единственно возможными. Могут существовать альтернативные оптимальные решения.

Общую задачу линейного программирования (ЗЛП) можно представить видом:


, где

- целевая функция;

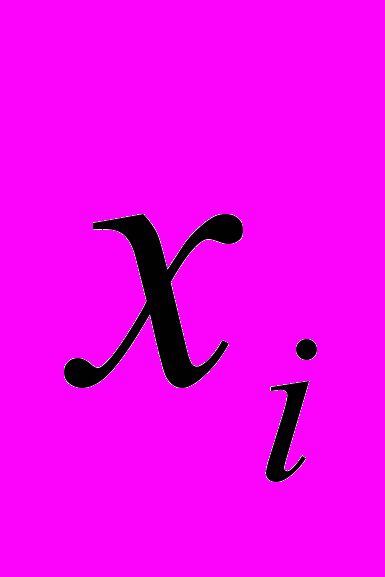.- управляемая переменная;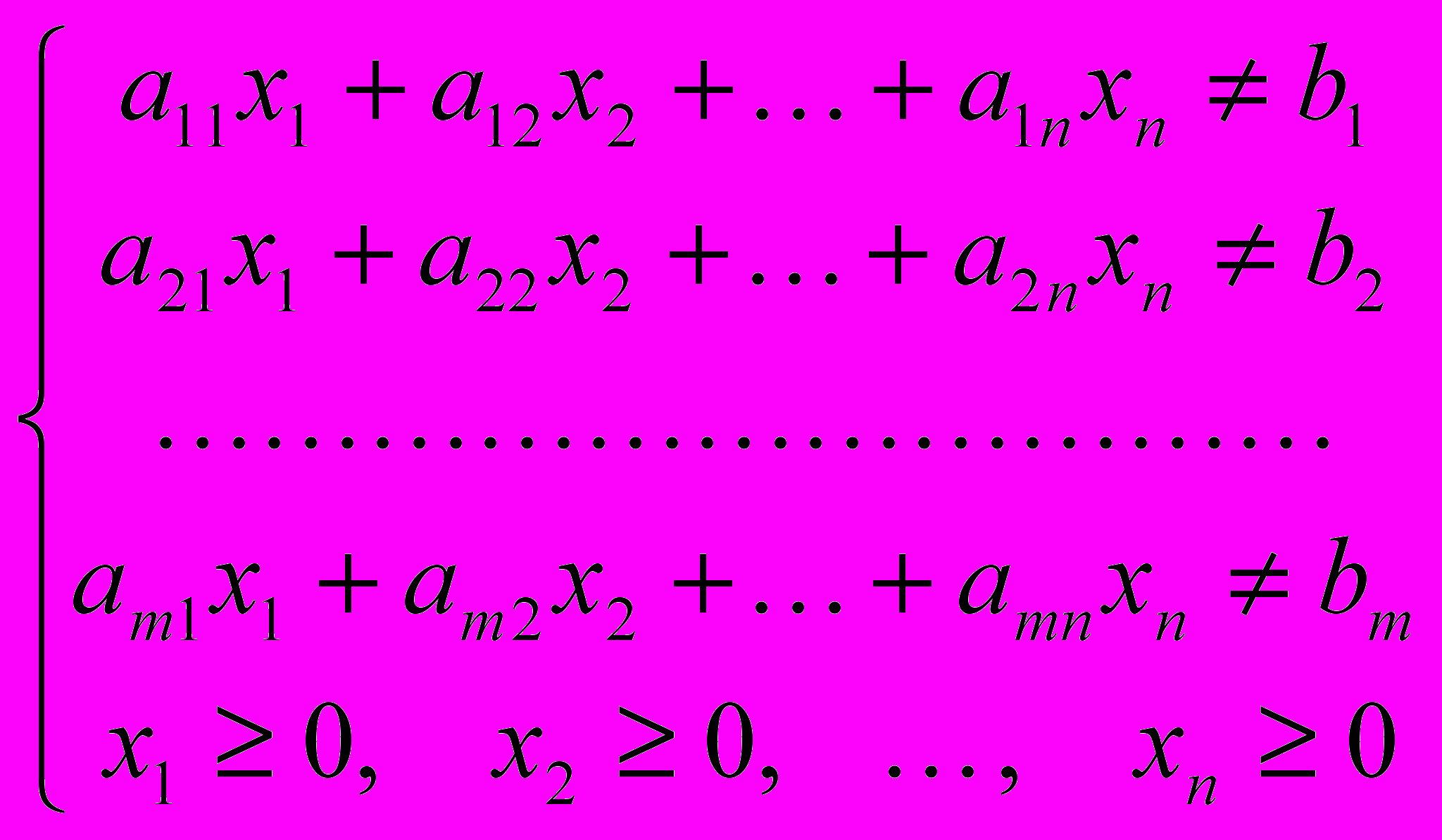




- система ограничений, ее матрица имеет ранг r  n.

Неотрицательное решение 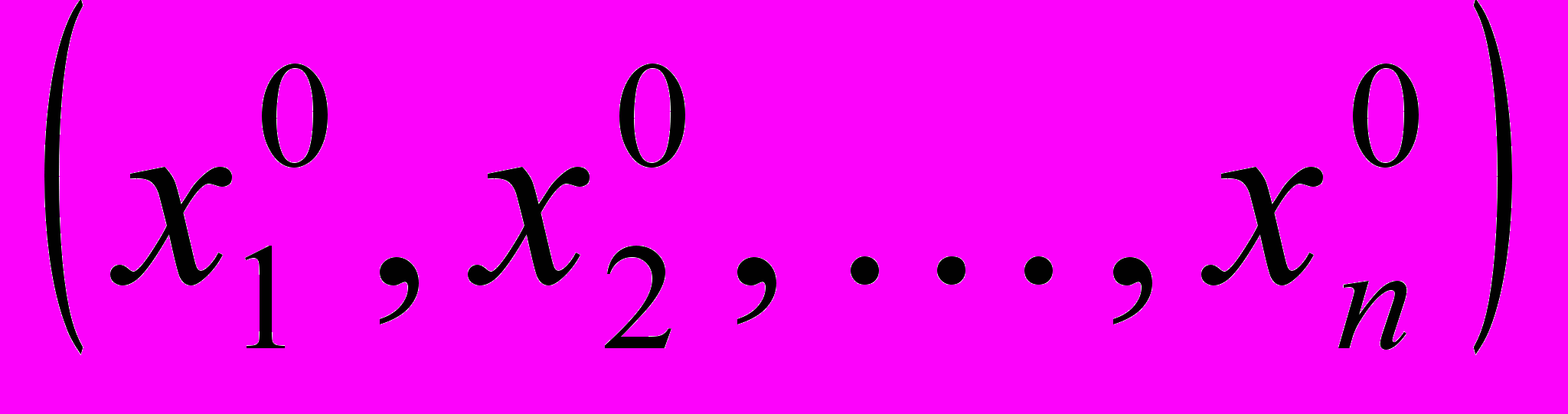системы (1) называется допустимым решением (планом) задачи. Допустимое решение называется оптимальным, если оно обращает целевую функцию (2) в min или max.

Существует несколько способов решения задачи ЛП, наиболее часто используют симплекс-метод.
^

Моделирование задач оперативного управления.

Задачи оперативного управления относятся к числу микроэкономических задач управления. К задачам оперативного управления относят задачи:

• распределение ресурсов (разработка правил управления запасами, устанавливающих момент пополнения запасов и размер пополняющего заказа);
  
• управление запасами (определение необходимого объема запасных частей, гарантирующего эффективное использование дорогостоящего оборудования);
  
• разработка принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию.
  
• распределение капитальных вложений между возможными новыми направлениями их использования.
  
• выбор методов проведения рекламной компании,
  
• систематизация методов поиска ценного вида ресурсов.
  
• составление календарных планов текущего и капитального ремонта сложного оборудования.
  
• разработка правил замены выбывающих из эксплуатации основных фондов.
  

Для решения таких задач широко используют методы динамического программирования (ДП). ДП - это математический аппарат, разработанный с целью повышения эффективности вычислений при решении задач математического программирования путём их разложения (декомпозиции) на относительно большие и, следовательно, менее сложные подзадачи. Каждая подзадача представляется этапом, с которым ассоциирована одна управляемая переменная 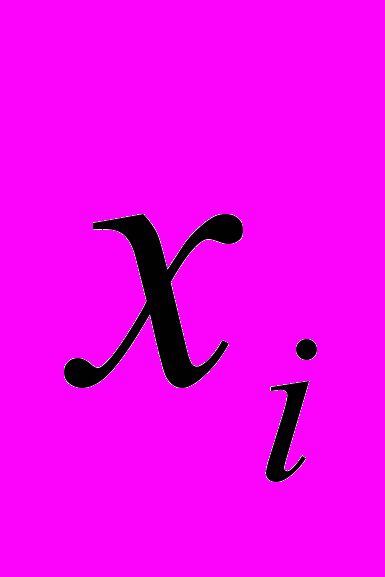. Набор рекуррентных вычислительных процедур, связывающих все этапы, обеспечивает получение допустимого оптимального решения задачи в целом при достижении последнего этапа.

Этапы построения модели ДП:

1. определение этапов решения задачи и управляемых переменных 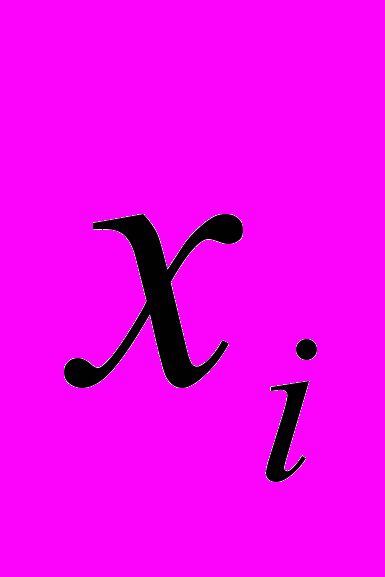на каждом этапе;
   
2. определение на каждом этапе вариантов решения (альтернатив);
   
3. определение состояний на каждом этапе.
   

Выбор состояний на этапах связан с определением вида зависимости между этапами (какая информация необходима для того, чтобы получить допустимые решения на текущем этапе без повторной проверки решений, принятых на предыдущих этапах?).


В общем случае, рекуррентные вычисления динамического программирования имеют вид (алгоритм прямой прогонки):


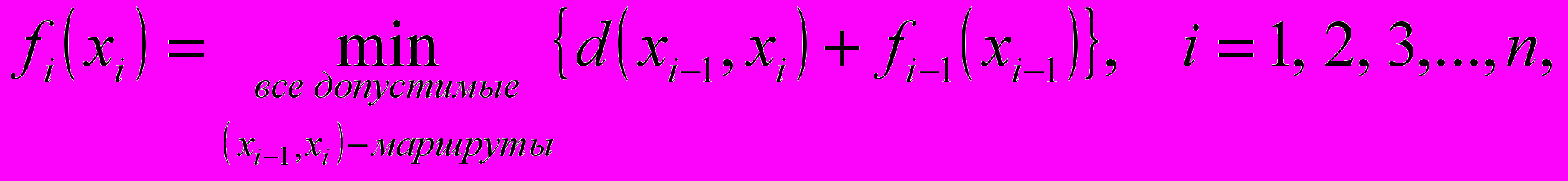где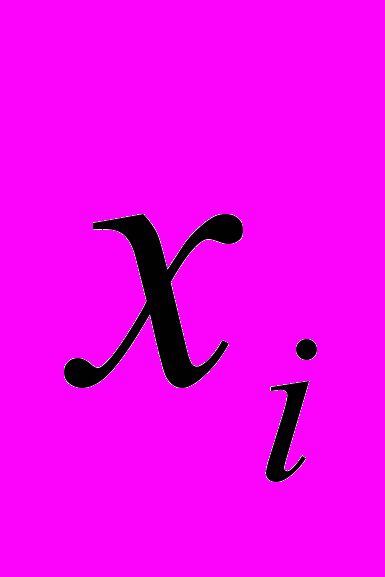

- состояние на этапе ,

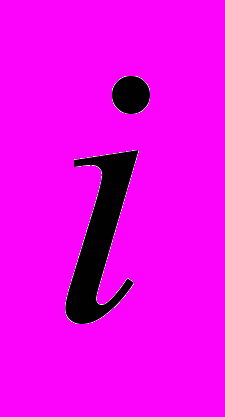–целевая функция от состояний на этапах 1, 2, ..., ,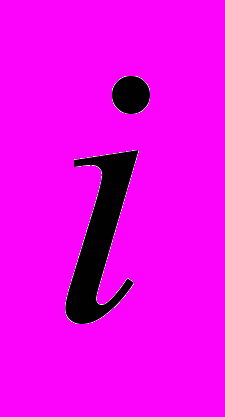

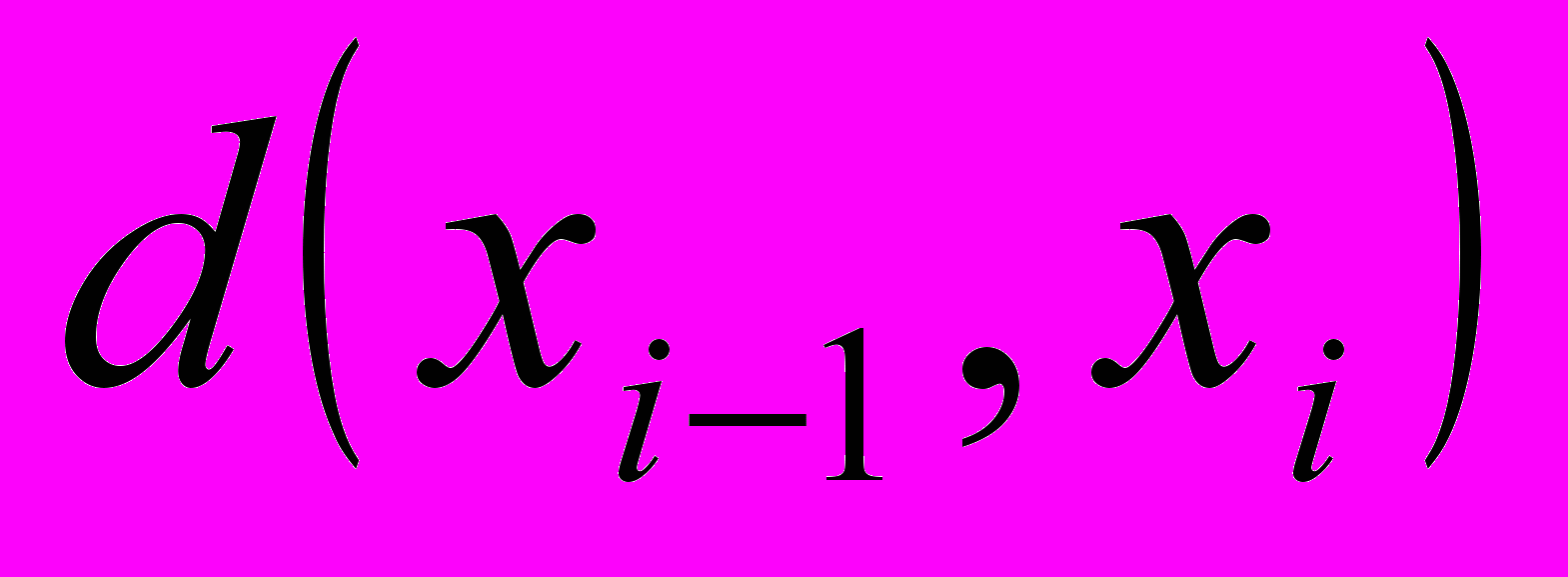– расстояние от состояния 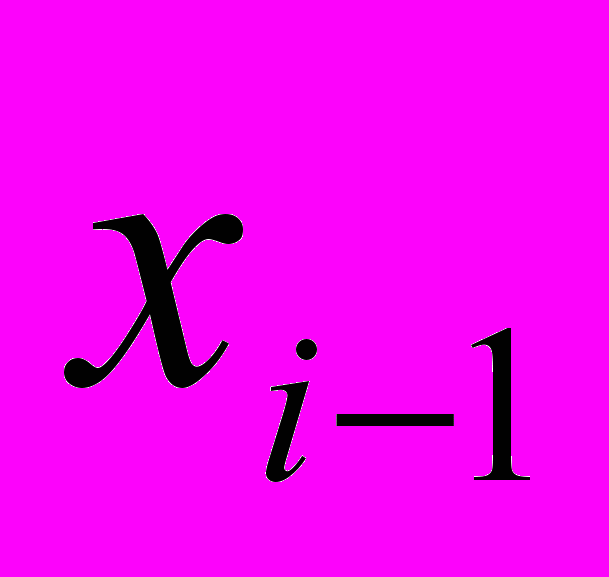до состояния ,

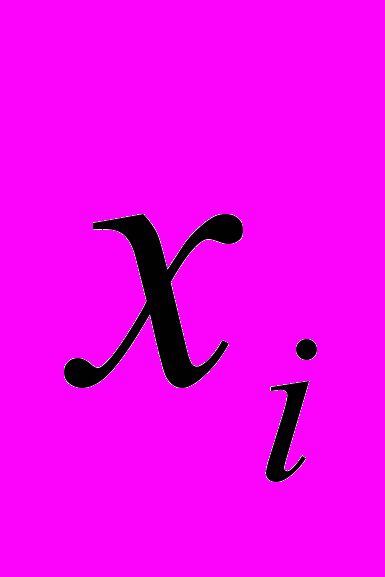– количество этапов.

При полагаем .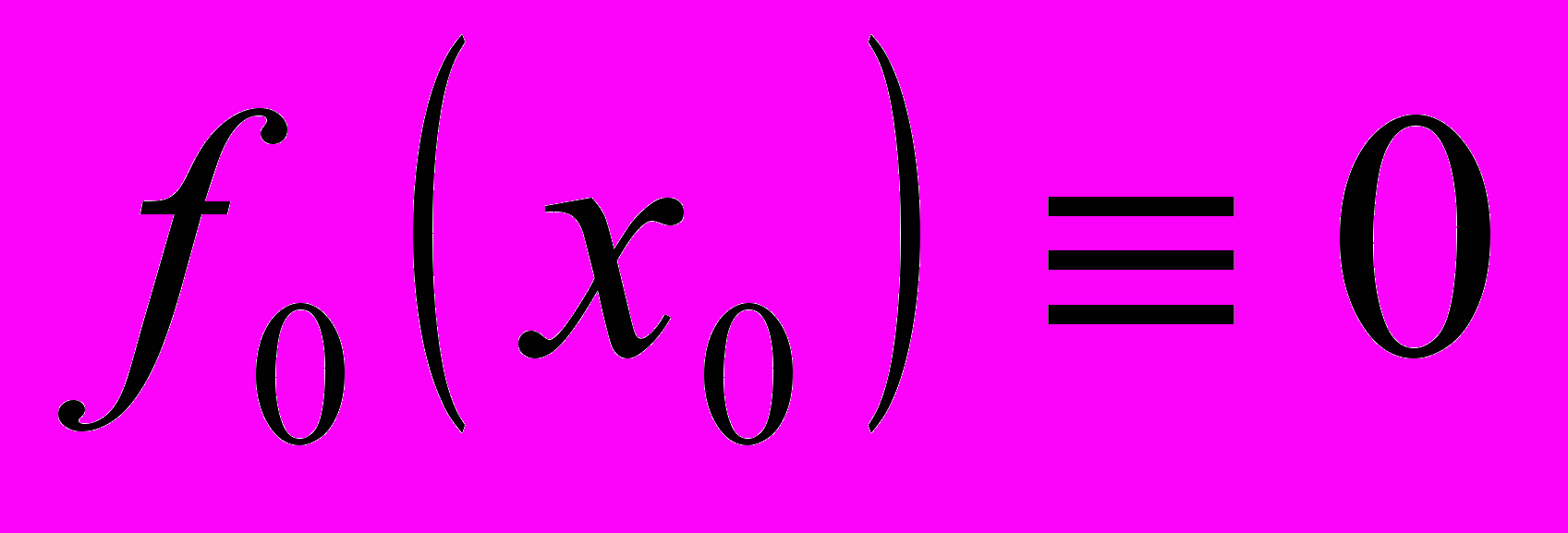

Фундаментальным принципом, положенным в основу теории ДП, является принцип оптимальности: каким бы ни был путь достижения некоторого решения (состояния), последующие решения должны принадлежать оптимальной стратегии для части пути, начинающейся с этого состояния, т.е. каждом этапе оптимальная стратегия определяется независимо от стратегий, применённых на предыдущих этапах.

. Можно проводить вычисления в обратном порядке, начиная с последнего этапа. Такой алгоритм называется алгоритмом обратной прогонки. Алгоритмы прямой и обратной прогонки приводят к одному и тому же решению. Алгоритм прямой прогонки представляется более логичным, но алгоритм обратной прогонки может быть более эффективным с вычислительной точки зрения.

Рекуррентное уравнение для алгоритма обратной прогонки имеет вид



^

Сетевые модели

Методы анализа сетей являются мощным математическим средством для решения технологических, конструкторских проектных и экономических задач. Достоинства этих методов – это их наглядность и логическая обоснованность, естественный подход к решению поставленных задач, малые вычислительные затраты как по времени, так и памяти. Сетевые модели в виде графов могут точно описывать многие реально существующие системы. Такие модели более понятны практикам, чем другие методы исследования операций.

Сетевые методы позволяют решать задачи проектирования больших оросительных систем, вычислительных комплексов, транспортных систем, систем связи, практические задачи, связанные со складированием, распределением товаров, календарным планированием выполняемых работ (сетевые графики проекта), заменой оборудования, контролем издержек, перевозками, работой систем массового обслуживания, обеспечением ритмичности производственного процесса, управлением запасами, распределением рабочей силы, реализацией операционных систем, реализацией СУБД с большими объемами информации, планированием семейного бюджета и т.д.

По сравнению с другими методами оптимизации, сетевые алгоритмы позволяют решать задачи со значительно большим числом переменных и ограничений. Сетевые алгоритмы позволяют находить более эффективные решения при изучении больших систем.

^

Модели управления проектами

Сетевые модели широко используют для управления проектами, в частности с помощью метода сетевого планирования и управления осуществляется планирование технической подготовки производства. Эти методы применимы к проектам, когда для достижения определенной цели должна выполняться упорядоченная последовательность заданий. Существует два метода управления проектами:

• метод критического пути (МКП);
  
• метод оценки и пересмотра планов (ПЕРТ).
  

Ограничения методов:

• проект должен состоять из хорошо определенной совокупности заданий, выполнение которых означает завершение проекта;
  
• задания упорядочены таким образом, что должны выполняться в определенной последовательности;
  
• продолжительность выполнения заданий известна или может быть определена.
  
• предполагается, что начатая работа продолжается без перерыва до завершения;
  
• выполнение следующей работы не обязательно должно начаться сразу после завершения предыдущей, но оно не может начинаться до завершения предыдущей. (Это затрудняет применения методов в отраслях с непрерывным производственным циклом.)
  

Отличия методов: метод МКП требует, чтобы продолжительность имела единственное значение, а метод ПЕРТ разрешает устанавливать верхний и нижний пределы продолжительности выполнения заданий. Методы различаются по способам задания срока завершения.

Для построения сетевой модели комплекс работ проекта разделяется на работы. Сетевая модель отображает логическую взаимосвязь и параметры всех работ и событий. Существует два способа построения моделей проекта: модель узел-событие, модель узел-работа.

В сетевой модели типа узел-событие понятие работа на сетевом графике означает процессы или совокупность процессов. Работа – стрелка (ориентированная дуга). Отношения упорядочения между работами задаются с помощью событий. Кружки – свершение событий, отражающих результаты выполнения работ. Событие определяется, как момент времени, когда завершаются одни работы и начинаются другие. Начальная и конечная точки любой работы описываются парой событий 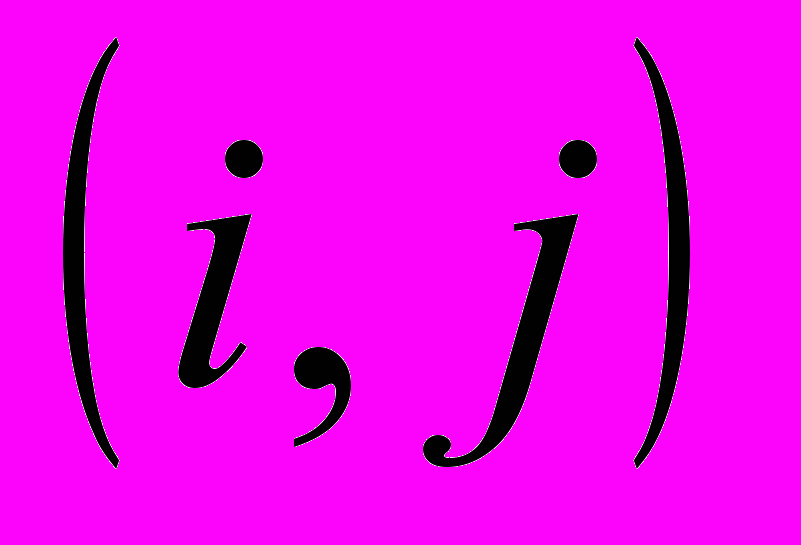(см. рис. 6.1). Операции, выходящие из некоторого события, не могут начаться, пока не будут завершены все операции, входящие в это событие.




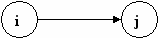III


Рис. 6.1 – Фрагменты сетевой модели

Понятие работа может иметь следующие значения:

• работа (действительная работа) – трудовой процесс, требующий затрат времени и ресурсов;
  
• ожидание – процесс, требующий затрат времени, но требующий затрат ресурсов;
  
• фиктивная работа - не требует затрат времени и ресурсов (она вводится для отражения логической связи работ, показывает точную очередность их выполнения, на графике отображается штриховой линией);
  

Продолжительность выполнения работы может быть определена по нормативам времени. Если это невозможно, то ответственный исполнитель дает в зависимости от принятой системы три или две вероятностные оценки времени выполнения работ.

В системе с тремя оценками проводится статистическая обработка на основе допущения, что вероятность получения ожидаемой продолжительности работы подчиняется закону -распределения:

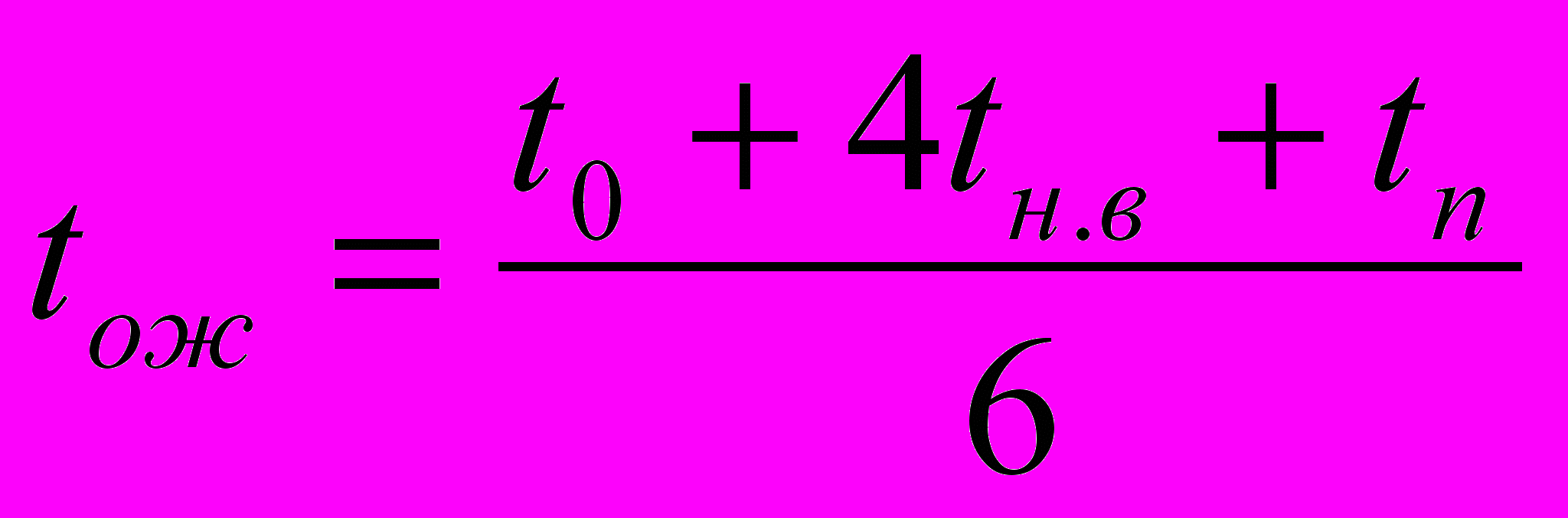, (6.1)

где

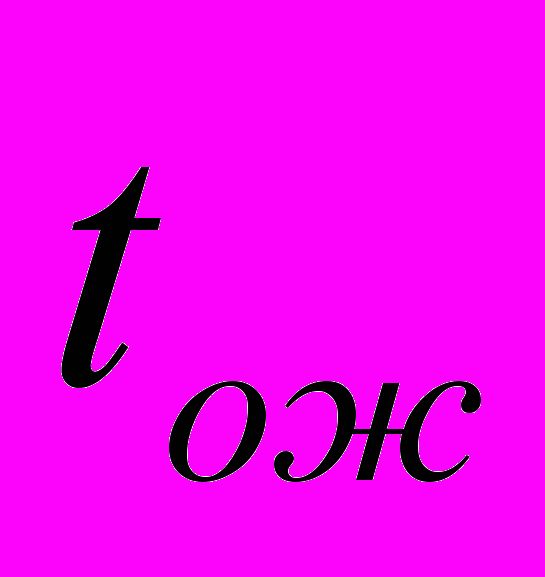- ожидаемая продолжительность работы;

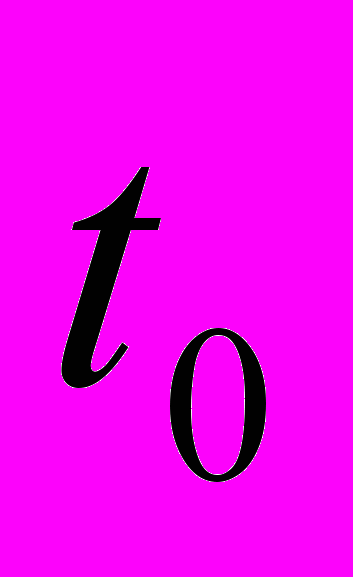- оптимистическая оценка времени;

- наиболее вероятная оценка времени;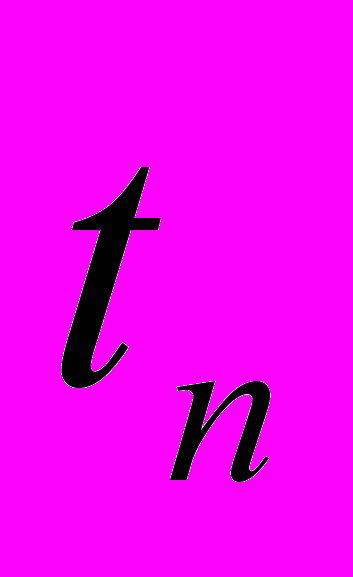

- пессимистическая оценка.

Для определения возможной величины разброса ожидаемого времени (вероятности отклонения от рассчитанного значения) находится дисперсия:


, (6.2)


В системе с двумя оценками:


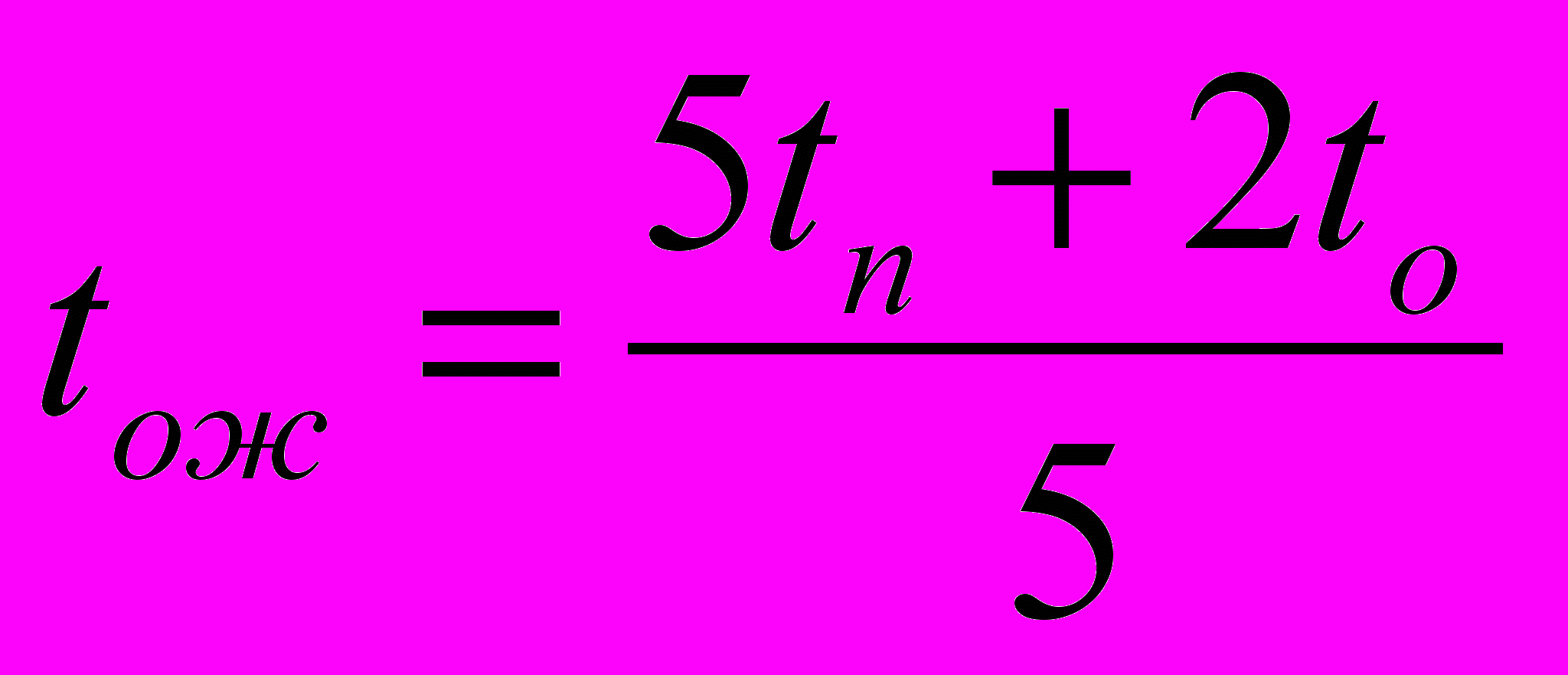, (5.3)


Исходное событие – начало выполнения комплекса работ. Завершающее событие- достижение конечной цели комплекса работ. Всякая работа сетевого графика соединяет два события. В отличие от работы событие не является процессом и не имеет продолжительности. Событие не может наступить, пока не закончатся предшествующие ему работы.

Последовательность работ в сети называется путем. Продолжительность любого пути равна сумме продолжительностей составляющих его работ. Минимальная продолжительность работ проекта определяется последовательностью работ проекта, составляющих самый длинный путь через сеть. Такой путь, определяющий общую продолжительность, называется критическим. Любое увеличение их продолжительности или любая задержка в их выполнении увеличивают время выполнения всего проекта. Чтобы сократить сроки выполнения комплекса работ, необходимо сократить сроки выполнения работ, лежащих на критическом пути.
^

Разновидности сетевых графиков.

Сетевые графики, имеющие одно завершающее событие, называются одноцелевыми, несколько – многоцелевые. Сетевой график может иметь детерминированную, случайную или смешанную структуру.

Проведение работ по сетевому планированию и управлению осуществляется в следующем порядке:

• определение состава работ комплекса, их взаимосвязи и последовательности выполнения работ по этапам;
  
• составление сетевого графика на комплекс работ по этапам;
  
• определение критического пути и резервов времени;
  
• оценка всех типов ресурсов и потребной суммы ассигнований с распределением по этапам работ;
  
• составление календарного плана комплекса работ;
  
• анализ и оптимизация календарного плана – разработка мероприятий по сокращению времени критического пути, доведение времени критического пути до планового;
  
• составление окончательного проекта календарного плана;
  
• управление ходом работ с помощью календарного плана.
  

^

Расчет сетевой модели

Для построения календарного плана определяются сроки начала и окончания каждой работы. В результате вычислений определяются критические и некритические работы проекта. Работа считается критической, если задержка ее начала приводит к увеличению срока окончания всего проекта. Некритическая работа отличается тем, что промежуток времени между ее ранним началом и поздним окончанием (в рамках рассматриваемой задачи программы) больше ее фактической продолжительности. В таком случае говорят, что некритическая работа имеет резерв или запас времени.

Конечным результатом выполняемых на сетевой модели расчетов является календарный график (план). При этом необходимо учитывать наличие ресурсов, т.к. одновременное (параллельное) выполнение некоторых операций из-за ограничений, связанных с рабочей силой, оборудованием и другими видами ресурсов, может оказаться невозможным. Сдвигая некритическую работу в том или ином направлении, но в пределах ее полного резерва времени, можно добиться снижения максимальной потребности в ресурсах или для выравнивания потребностей в ресурсах на протяжении всего срока реализации программы.

Задача заключается в построении такого календарного плана, при котором потребности в рабочей силе будут наиболее равномерными на протяжении всего срока осуществления программы.

Иногда может ставиться цель не просто обеспечения равномерного использования ресурсов, а ограничение максимальной потребности в них определенным пределом. Если этой цели не удается достичь путем перепланирования календарных сроков некритических операций, то, чтобы снизить потребность в ресурсах, приходится увеличивать продолжительность некоторых критических операций.

При календарном планировании можно учесть еще вероятностный характер оценок продолжительности операций и в явном виде стоимостные факторы. Стоимостный аспект вводится в схему календарного планирования программ путем определения зависимости «затраты (стоимость) - продолжительность» для каждой операции программы. При этом рассматриваются только элементы так называемых прямых затрат, а косвенные затраты типа административно-управленческих расходов не принимаются во внимание. Однако их влияние учитывается при выборе окончательного календарного плана. На этапе реализации программы календарный план может нарушаться. Необходимо корректировать (обновлять) сеть, приписывая нулевые значения продолжительностям уже законченных операций, а частично выполненным операциям – оценки продолжительности, соответствующие их незавершенному объему. В сеть вводятся также структурные изменения, т.е. исключаются операции, которые по каким-либо причинам стали излишними, и вводятся операции, не предусмотренные ранее, но необходимые в будущем. Затем производят обычные вычисления на сети и определяют новый календарный план. В реальных условиях частые корректировки календарного плана, как правило, требуются на начальном этапе реализации программы. Затем процесс ее выполнения переходит в установившийся режим и число требуемых корректировок календарного плана существенно сокращается.