Geum.ru

Остроухова Елена Геннадьевна, учитель математики высшей кк урок

Вид материалаУрок

Содержание


Ход урока
Площадь многоугольника –
По свойству площадей
Значит, MC=AB
Чертеж, доказательство.
Подобный материал:
МОУ СОШ №54 с углубленным изучением предметов социально – гуманитарного цикла

Остроухова Елена Геннадьевна, учитель математики высшей кк

Уроки геометрии в 8 классе по теме «Площадь»


Изложение материала представлено крупным блоком в виде лекции в течение двух уроков по 45 минут каждый, охватывающей первые два параграфа темы «Площадь». Лекция сопровождается презентацией, содержащей доказательство теорем, примеры решения задач. Лекция конспектируется учащимися.
Такой подход позволяет отвести на изучение теории 2 часа, на решение типовых задач 2 часа, задач повышенного уровня 2 часа, задач продвинутого уровня 2 часа (или эти 2 часа отвести ученику на подготовку проекта по применению темы «Площадь»).

  • Цель: расширение и углубление представлений учащихся об измерении площадей, выведение формулы площади прямоугольника, параллелограмма, треугольника, трапеции, доказательство теорем об отношении площадей треугольников, имеющих равные высоты, угол.
  • Задачи: заложить базу для доказательства теоремы Пифагора и признаков подобия треугольников, расширить внутренние логические связи курса геометрии, научить использовать рисунки и чертежи на всех этапах обучения, продолжить развитие геометрической интуиции, развивать умение делать предположение, переносить знания в новую ситуацию.
  • Мотивация: есть различные геометрические фигуры. По каким параметрам их можно сравнивать? Что для этого надо уметь измерять или вычислять? Как это делать?

Ход урока
  1. Организационный момент.
    Вы знаете, какая фигура называется многоугольником, элементы многоугольника. Научились вычислять длины отрезков или углов, принадлежащих многоугольнику, выделять равные отрезки, углы, многоугольники. Что общего у квадрата со стороной 4 см и прямоугольника со сторонами 2 см и 8 см? Можно ли сравнить по каким – то параметрам такие многоугольники как параллелограмм и трапеция, треугольник прямоугольный и тупоугольный? Постараемся ответить на эти вопросы в ходе нашего урока.


  2. Изучение нового материала.
    Каждый понимает, что комната 20м² больше, чем 15м², Новосибирская область занимает площадь большую, чем город Новосибирск, для изображения взрослого человека в натуральную величину нужно взять бумаги больше, чем для изображения малыша. Понятие площади нам знакомо из повседневной жизни. Приведите примеры, где мы используем понятие площади. На уроке мы поговорим о площадях многоугольников. Рассмотрим, как измерить или вычислить площадь многоугольника, опираясь на некоторые теоретические положения.
    Далее рассмотрение материала проводим по презентации «Площадь». Основные формулировки, рисунки, чертежи, формулы учащиеся фиксируют в тетрадях. Решения задач (2) (кадр 9) проводим самостоятельно в парах, обсуждаем итоги решения задач (№2 имеет несколько способов решения, связанных с разным разбиением фигуры на части).


  3. Подводим итоги.
    Отвечаем на вопросы:
    Что общего у квадрата со стороной 4 см и прямоугольника со сторонами 2 см и 8 см?
    По каким параметрам можно сравнить параллелограмм и трапецию, треугольник прямоугольный и тупоугольный?
    Если отношение площадей прямоугольного и тупоугольного треугольника больше 1, что это означает?
    Выразите площадь прямоугольника со сторонами 15мм и 3,2 см целым числом.


  4. Домашнее задание.
    п.48, 50, 51, 52, 53.
    Знать наизусть формулировки основных понятий и свойства площадей, теорем, формулы вычисления площадей треугольника, квадрата, прямоугольника, параллелограмма, трапеции, единицы площади. Выучить доказательство теорем о площади параллелограмма, треугольника, трапеции. Разбор теорем об отношении площадей треугольников, имеющих равные высоты, или равные углы

    Примечание: на следующем уроке разбираем
    – п.49 в ознакомительном порядке,
    – применение теорем об отношении площадей треугольников, имеющих равные высоты, или равные углы:№473, №474, №479.

Пример конспекта ученика.


Площадь многоугольника –

часть плоскости, которую занимает многоугольник.

Единица площади – площадь квадрата.

1 дм2= 100 см2; 1м2 = 10 000 см2


1 см2 = 100 мм2; 1 м2 = 100 дм2


Свойства площадей:
  1. Равные многоугольники имеют равные площади.
  2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников
  3. Площадь квадрата равна квадрату его стороны.


№1.

Чертеж

Дано:

ABCD – параллелограмм

MC = CD

Доказать:

SABCD = SAMD


Решение:

т.K – пересечение AM и BC.

Параллелограмм ABCD состоит из DABK и трапеции AKCD.

DAMD состоит из D KMC и трапеции AKCD.

По свойству площадей

SABCD=SABK+SAKCD

SAMD=SKMC+SAKCD

В DABK и DKMC: MC=CD (по условию)

AB=CD (как противоположные стороны параллелограмма)

Значит, MC=AB

AB║DC, следовательно, ÐABK = ÐKCM как накрест лежащие при секущей BC.

BK=KC (по теореме Фалеса)

Следовательно, DABK = D MCK,

следовательно, SABK=SMCK,

следовательно, SABCD=SAMD

№2, №3. чертеж, решение



Площадь прямоугольника равна произведению его смежных сторон: S = ab

Чертеж, доказательство.

Площадь параллелограмма равна произведению стороны на высоту, к ней проведенную: S = ah

Чертеж, доказательство.

Площадь треугольника равна половине произведения стороны на высоту, к ней проведенную:

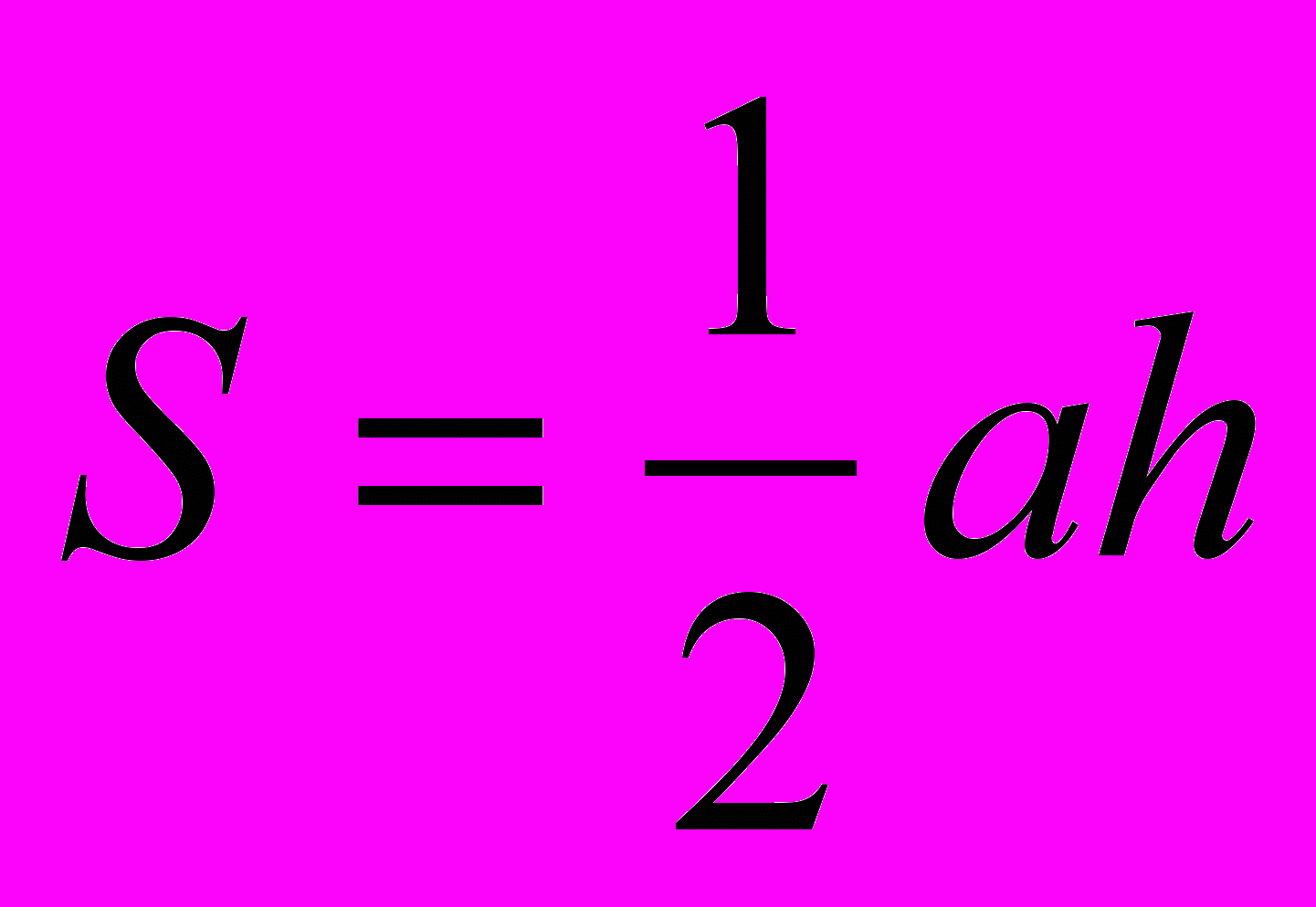
Чертеж, доказательство.

Площадь прямоугольного треугольника равна
половине произведения катетов

Чертеж, доказательство.

Отношение площадей треугольников, имеющих равную высоту, равно отношению их оснований.

Если треугольники имеют равные углы, то их площади относятся, как произведения сторон, содержащих эти углы.