Шошина Людмила Ивановна, учитель математики высшей квалификационной категории школы №887 зао урок
| Вид материала | Урок |
СодержаниеI. Историческая справка. II. Приращение функции. V. Дифференциал. |
- Хуснутдинова Накия Гараевна, учитель географии и биологии высшей квалификационной категории, 231.92kb.
- Зюхина Лариса Анатольевна, учитель биологии высшей квалификационной категории школы, 245.22kb.
- Норкина Светлана Юрьевна, учитель математики высшей квалификационной категории, педстаж, 62.83kb.
- Сечина Людмила Владимировна, учитель высшей категории моу «Петуховская средняя общеобразовательная, 612.61kb.
- Старостина Ирина Ивановна, учитель французского и немецкого языков высшей квалификационной, 130.25kb.
- Поваляева Галина Ивановна, учитель математики I(первой) квалификационной категории, 531.83kb.
- Максимова Людмила Петровна, учитель высшей квалификационной категории Смотерчук Елена, 2287.25kb.
- Барышева Ольга Ивановна, учитель истории и обществознания высшей квалификационной категории,, 83.43kb.
- Калита Людмила Ивановна учитель информатики высшей категории сш №23 Ленинского р-на, 237.8kb.
- Анализ работы рмо учителей иностранных языков 2010-2011 учебный год, 126.56kb.
Шошина Людмила Ивановна, учитель математики высшей квалификационной категории школы № 887 ЗАО
Урок-лекция с использованием компьютерных технологий по теме «Производная и дифференциал». 10 класс.
Цель урока: Познакомить учащихся с теоретической основой производной и дифференциала и практической направленностью этой темы.
Оборудование урока: компьютер, медиапроектор, экран, авторская презентация (слайды) к уроку, сделанная в программе Power Point. Лекция сопровождается демонстрацией слайдов на экране.
Продолжительность урока: 45 минут.
Эта тема в математике занимает важное место, именно здесь закладываются основы аналитического мышления, формируется соответствующая интуиция, развивается логика и культура использования функциональных обозначений и методов.
^ I. Историческая справка.
Предметом изучения математического анализа являются количественные соотношения действительного мира. Эти соотношения выражаются с помощью числовых величин, в арифметике это постоянные величины, а в анализе переменные величины. В основу изучения зависимости между переменными величинами кладут понятия функции и предела.
Методы математического анализа получили своё развитие в XVII веке. На рубеже XVII – XVIII веков Ньютон и Лейбниц, в общем и целом, завершили создание дифференциального и интегрального исчисления, а также положили основу учения о рядах и дифференциальных уравнениях. В XVIII веке Эйлер разработал последние два раздела и заложил основу других дисциплин математического анализа. К концу XVIII века накопился огромный фактический материал, но он был недостаточно разработан в логическом отношении. Этот недостаток был устранён усилиями крупнейших учёных XIX века, таких как Коши во Франции, Лобачевского в России, Абеля в Норвегии, Римана в Германии и других.
^ II. Приращение функции.
| Определение: | Разность 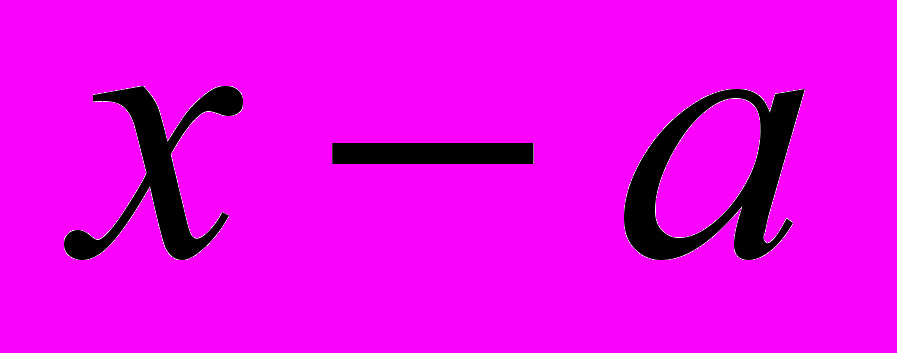 называется приращением аргумента при переходе от называется приращением аргумента при переходе от  к к 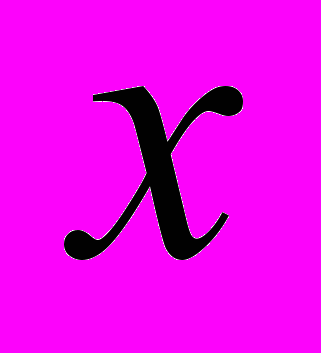 , а разность , а разность 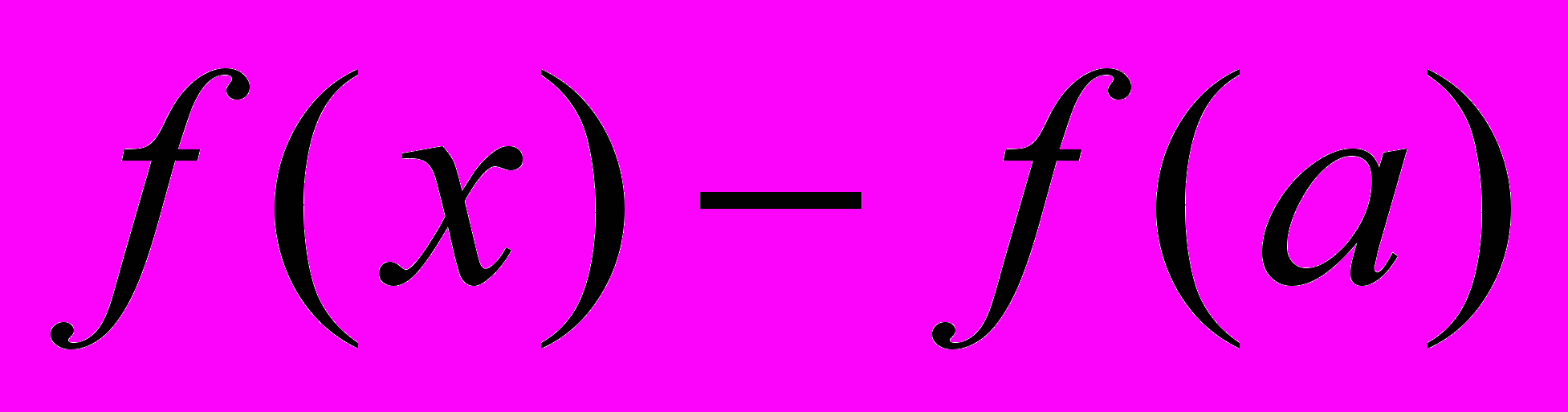 – приращением функции – приращением функции 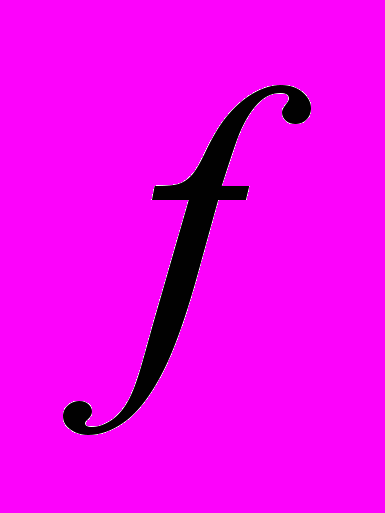 при этом переходе. при этом переходе. |

 y
y
 f(x) где
f(x) где 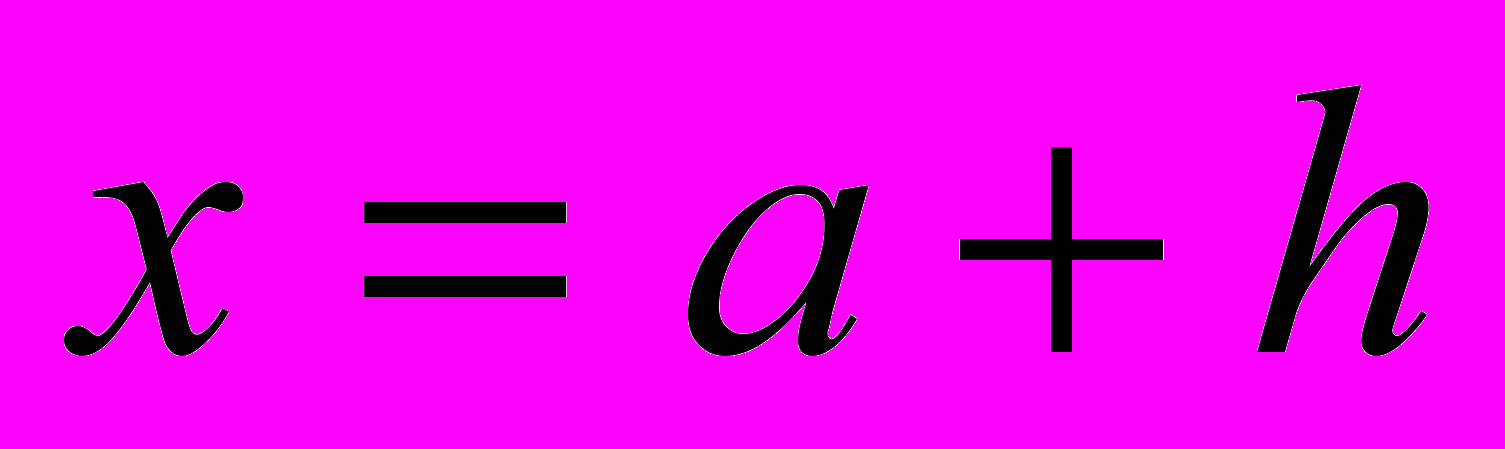
f(x)-f(a)
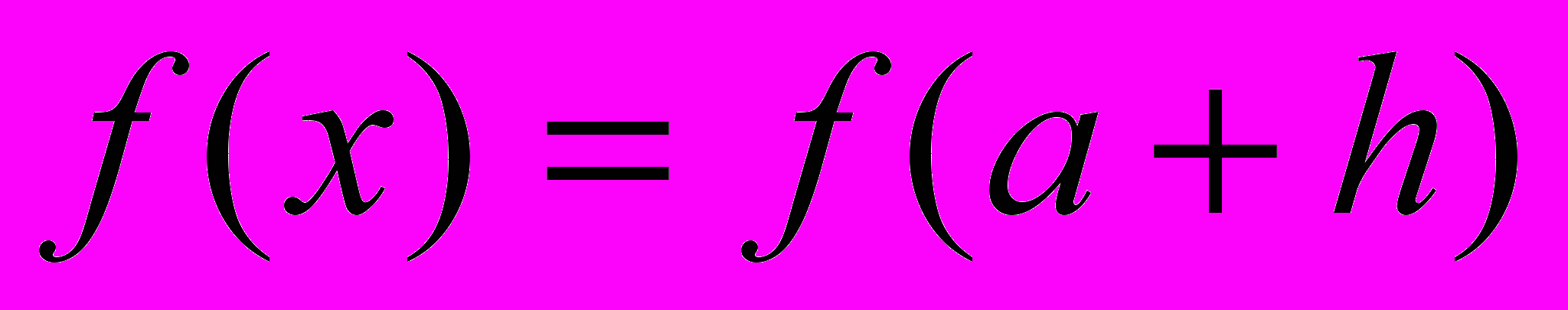

 f(a)
f(a)
0 a
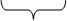 x x
x xh
Чтобы найти приращение функции f при переходе от a к a+h надо:
- найти значение функции f в точке a;
- найти значение функции f в точке a+h;
- из второго значения вычесть первое.
| Пример 1. | Найти приращение функции 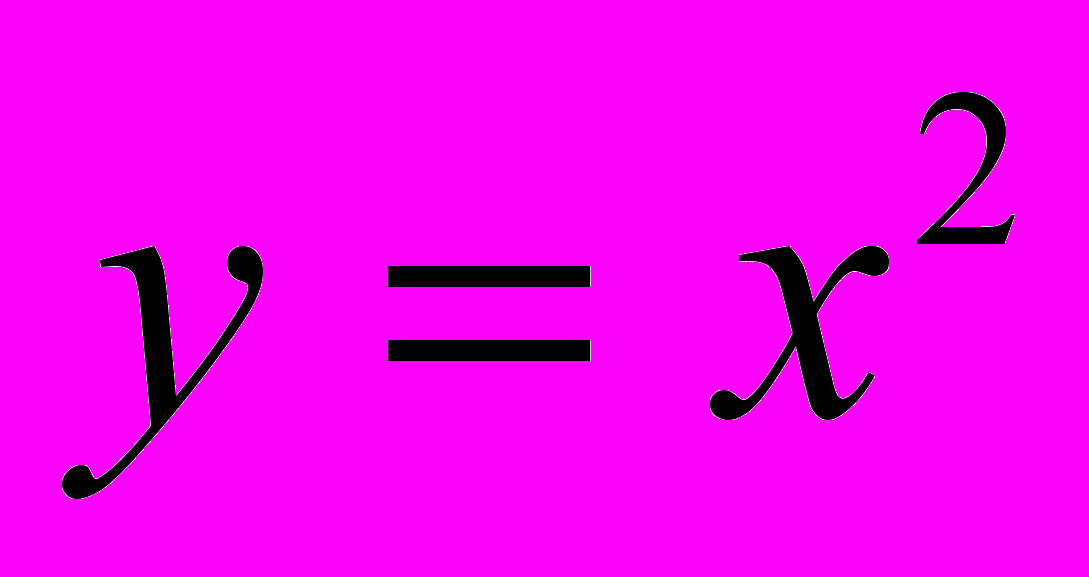 при переходе от при переходе от  к к 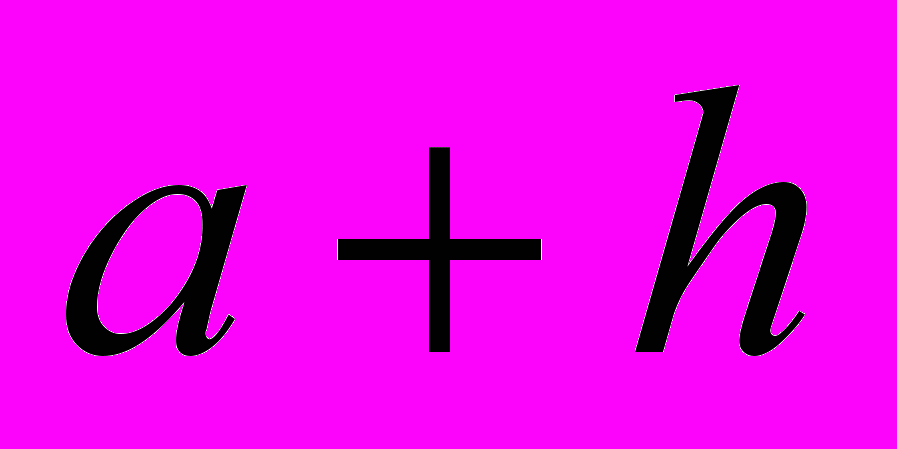 . . |
Решение.
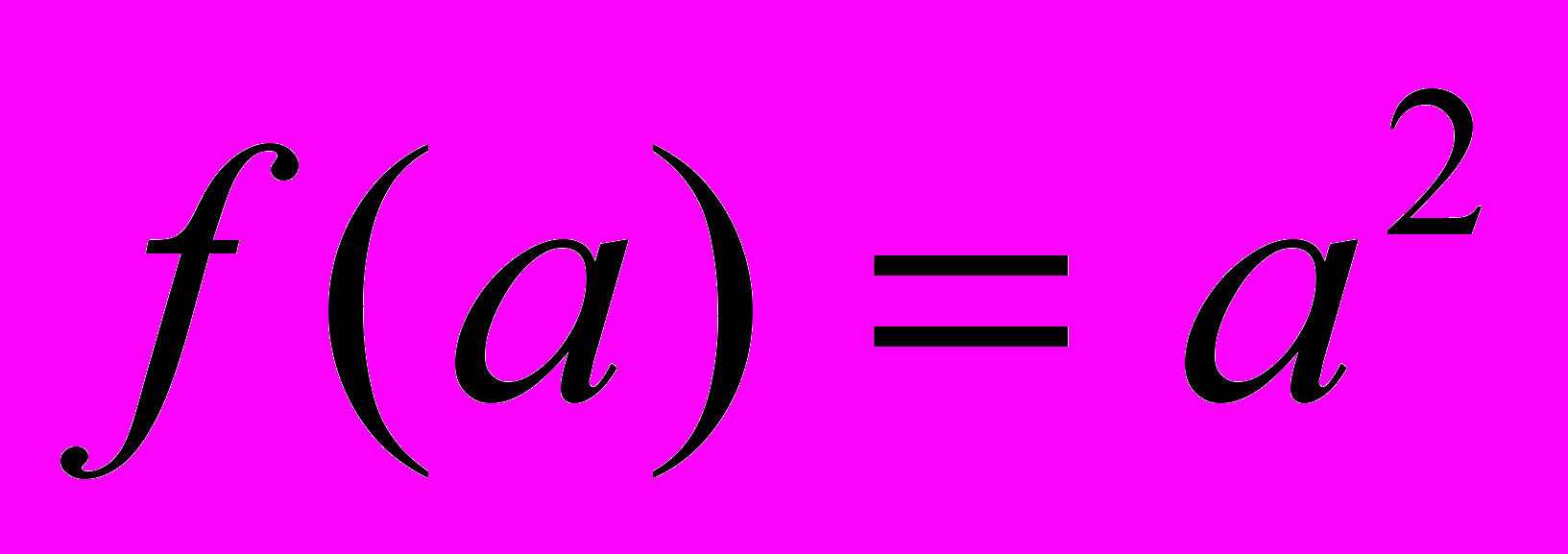
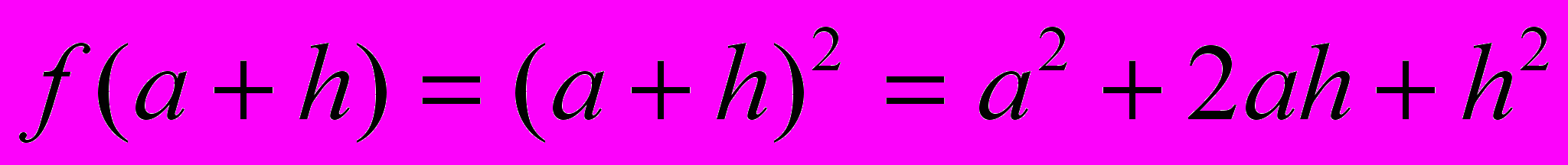
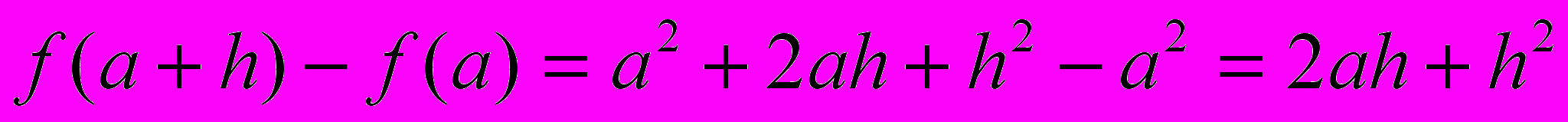
Ответ:
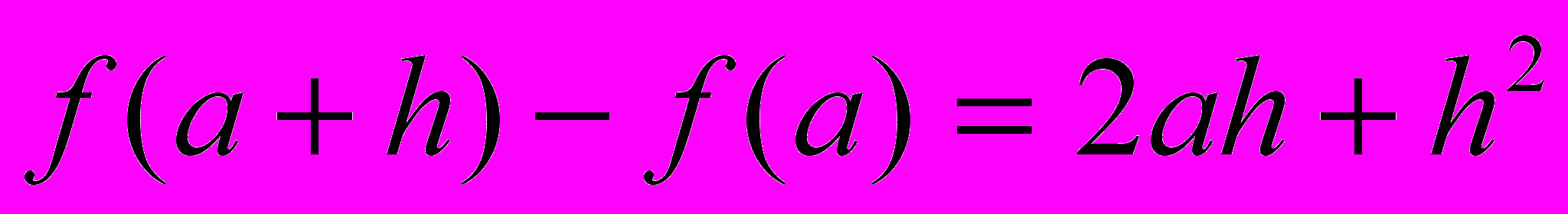 .
.III. Дифференцируемые функции.
Имеем график функции
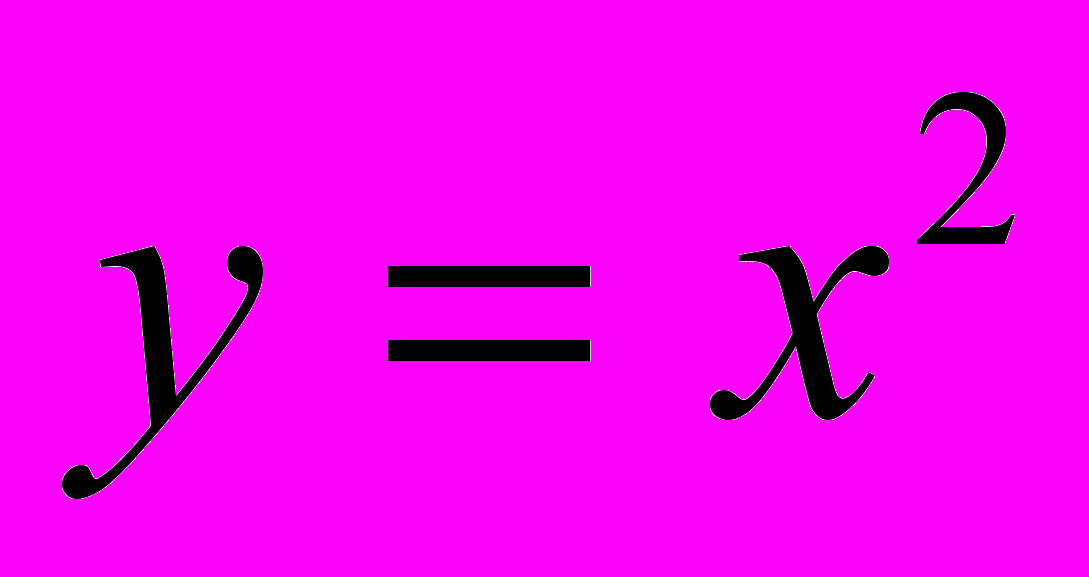 .
.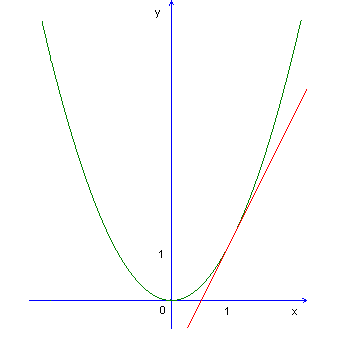
Если мы будем рассматривать достаточно малые промежутки, то график этой функции будет почти совпадать с прямой, то есть мы будем говорить об этой функции, что она дифференцируема (то есть линейна в малом).
| Определение: | Функция f называется дифференцируемой в точке а, если её приращение при переходе от  к к 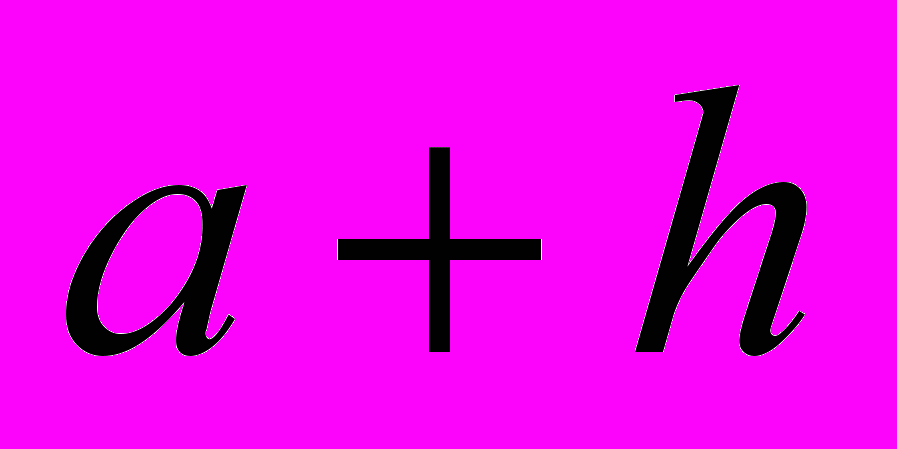 можно представить в виде: можно представить в виде:  где k – число, а функция α бесконечно мала при h→0. 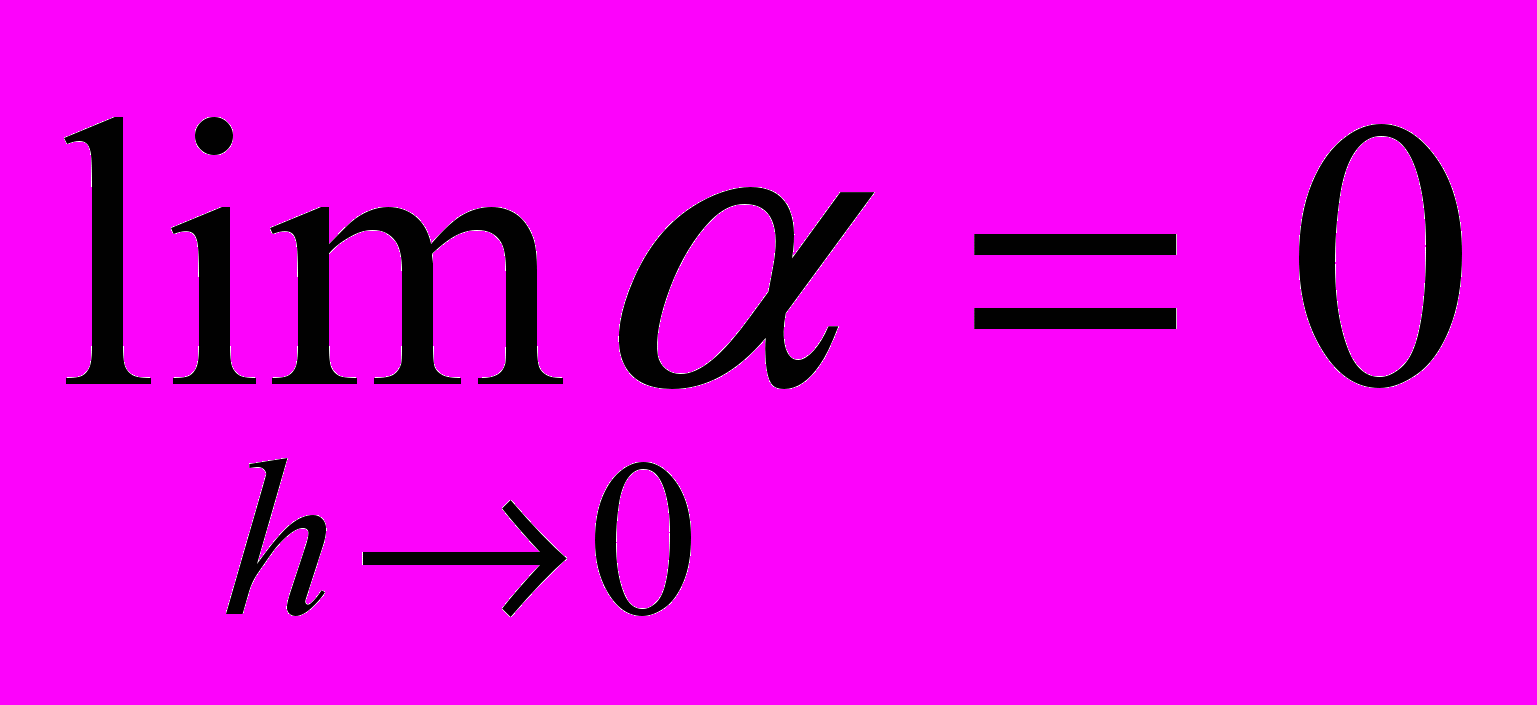 |
Линейная функция дифференцируема при любых значениях х.
| Пример 2. | Докажем, что функция 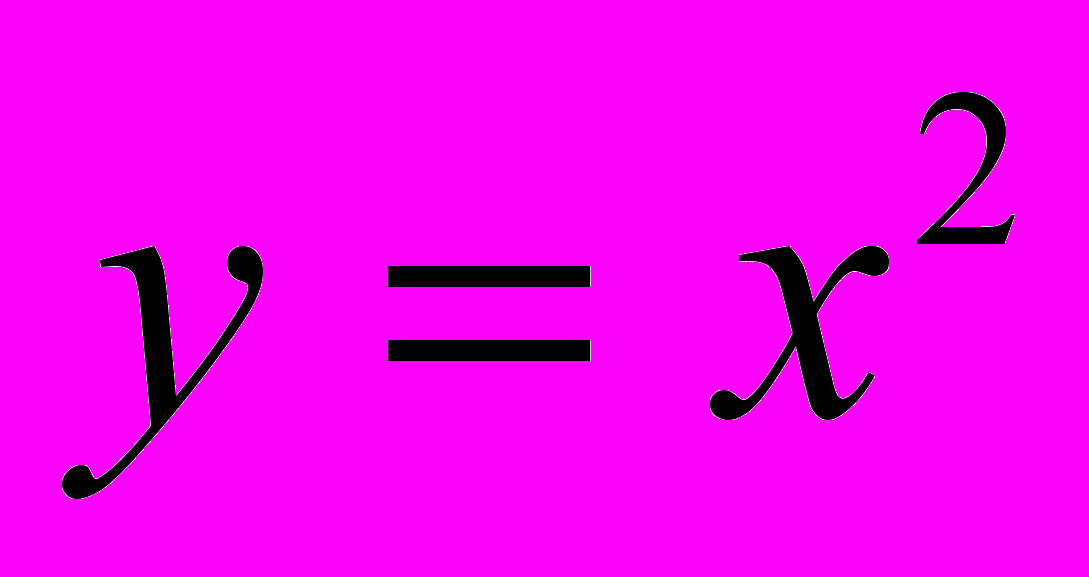 дифференцируема при любых значениях х. дифференцируема при любых значениях х. |
Решение.
В примере 1 приращение функции
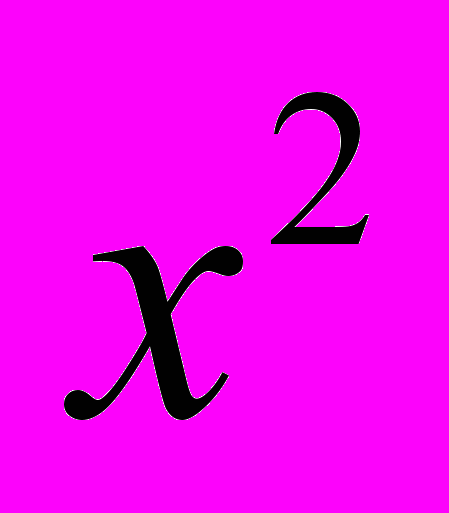 имеет вид
имеет вид 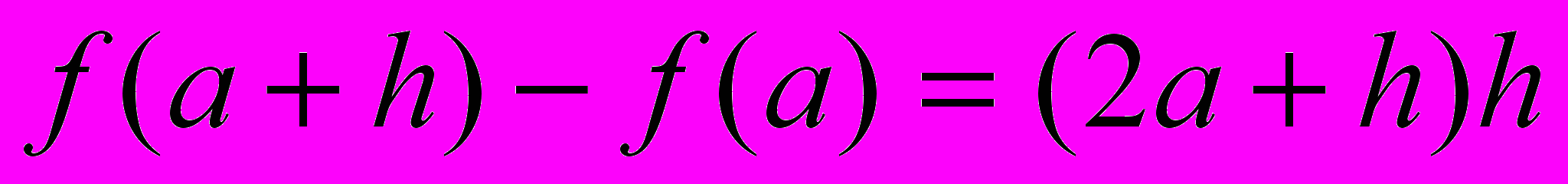
Если положить
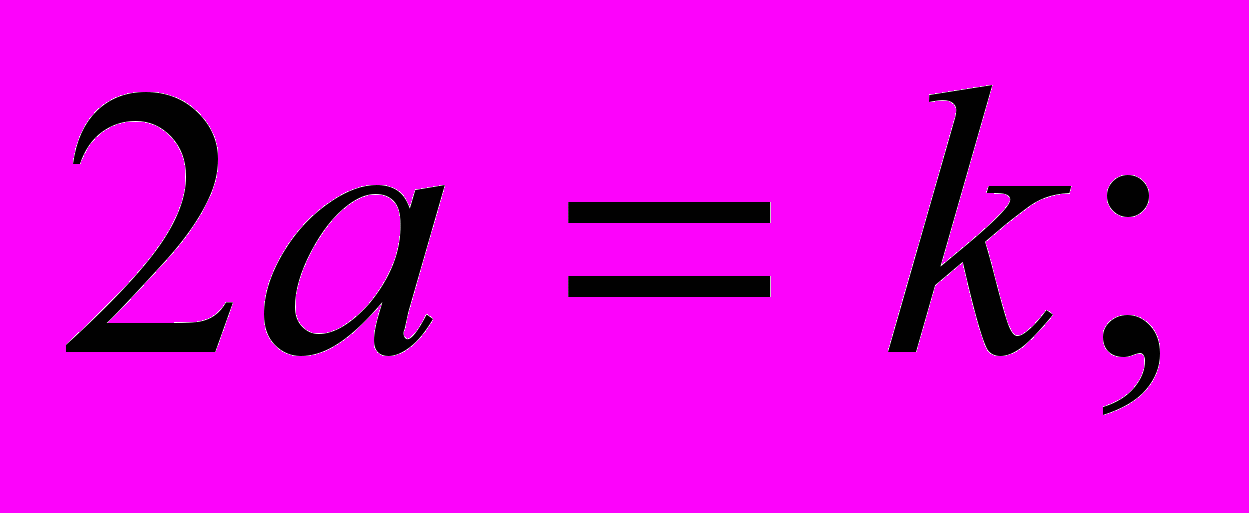
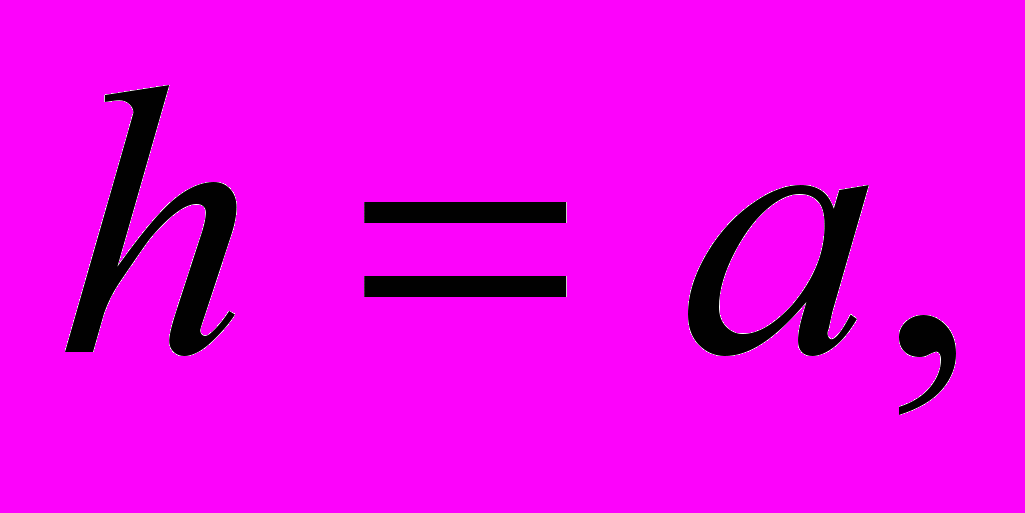 то правая часть равенства примет вид
то правая часть равенства примет вид 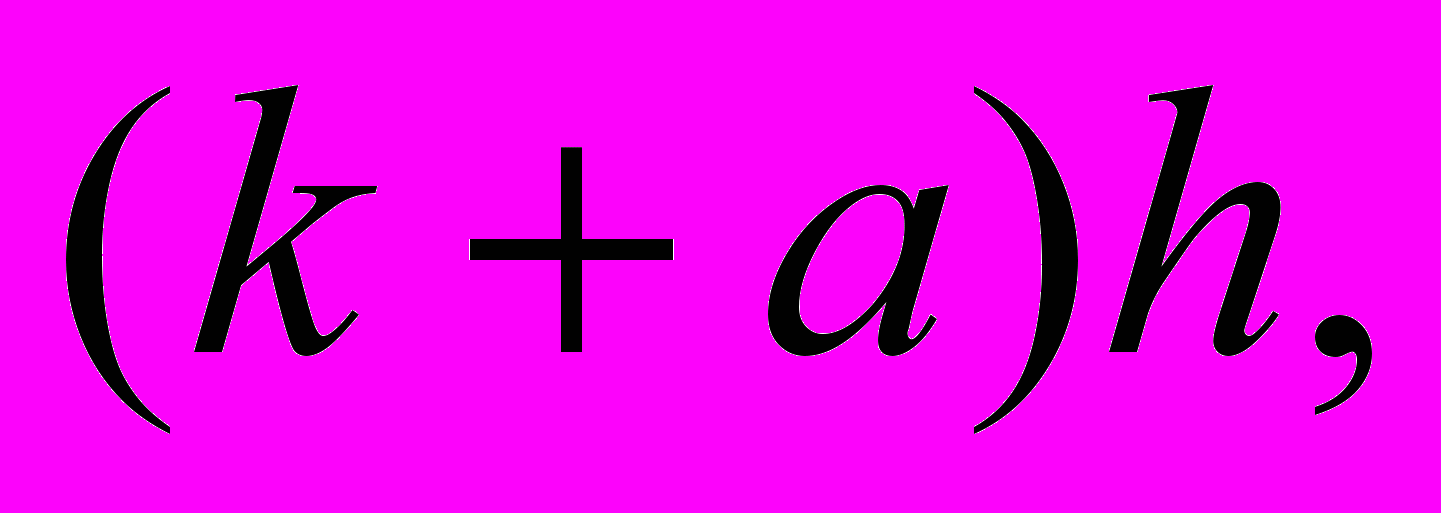 причём
причём 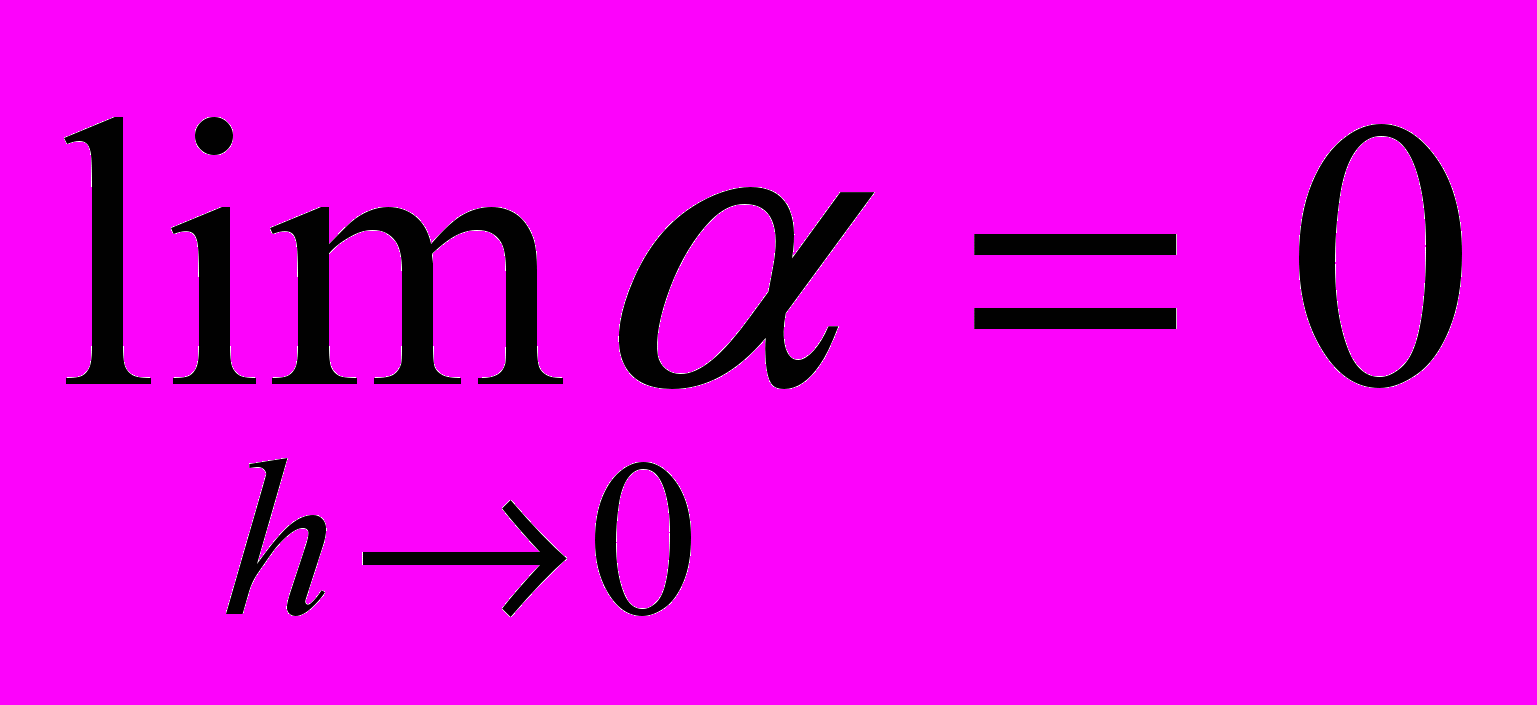 .
.Тем самым доказано, что функция
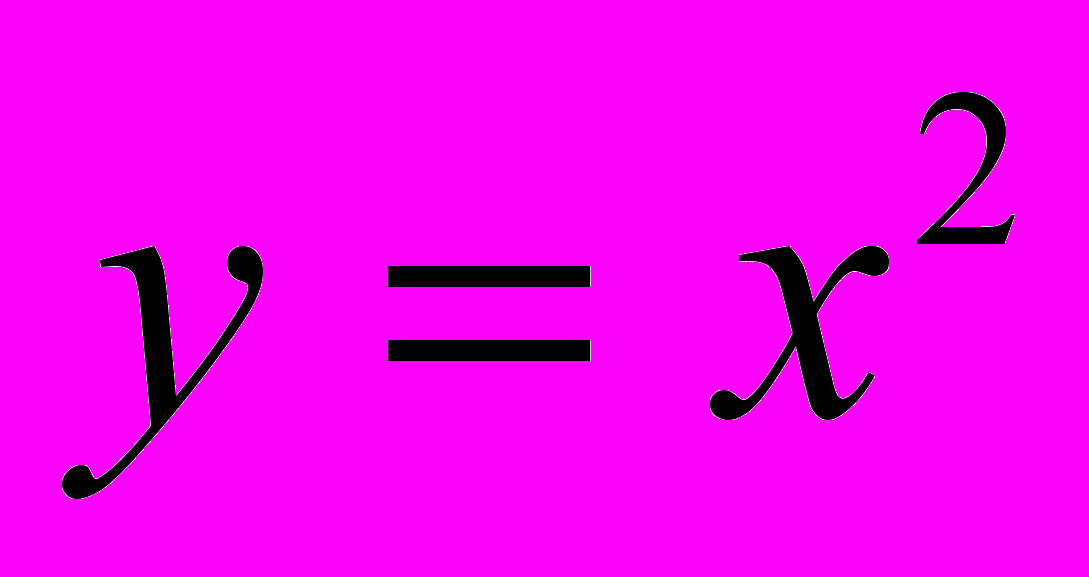 дифференцируема при всех х.
дифференцируема при всех х.Следующий пример выполняется учащимися самостоятельно в классе.
| Пример 3. | Докажем, что функция 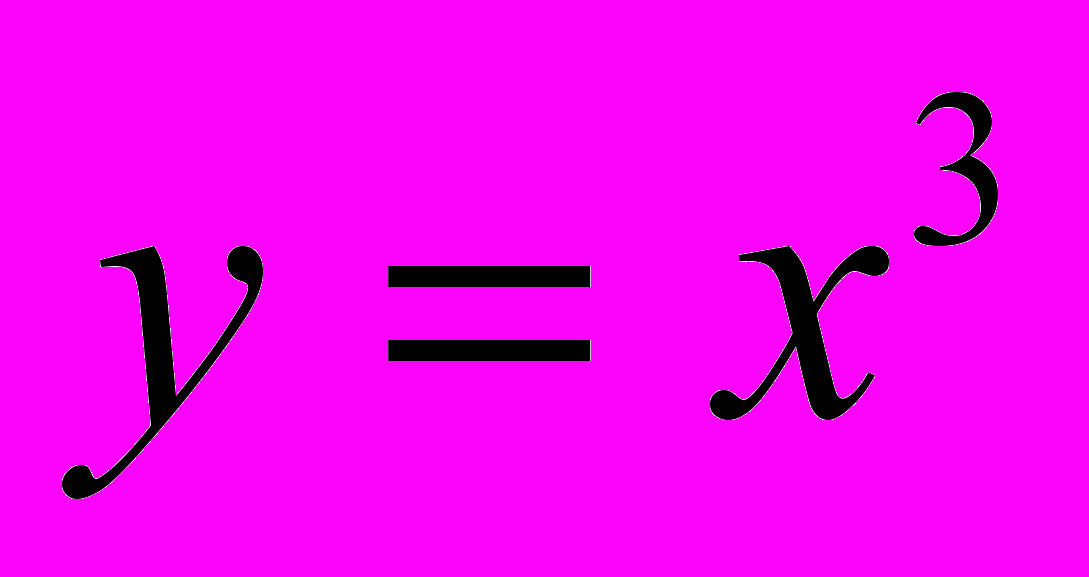 дифференцируема при любых значениях х. дифференцируема при любых значениях х. |
Решение.
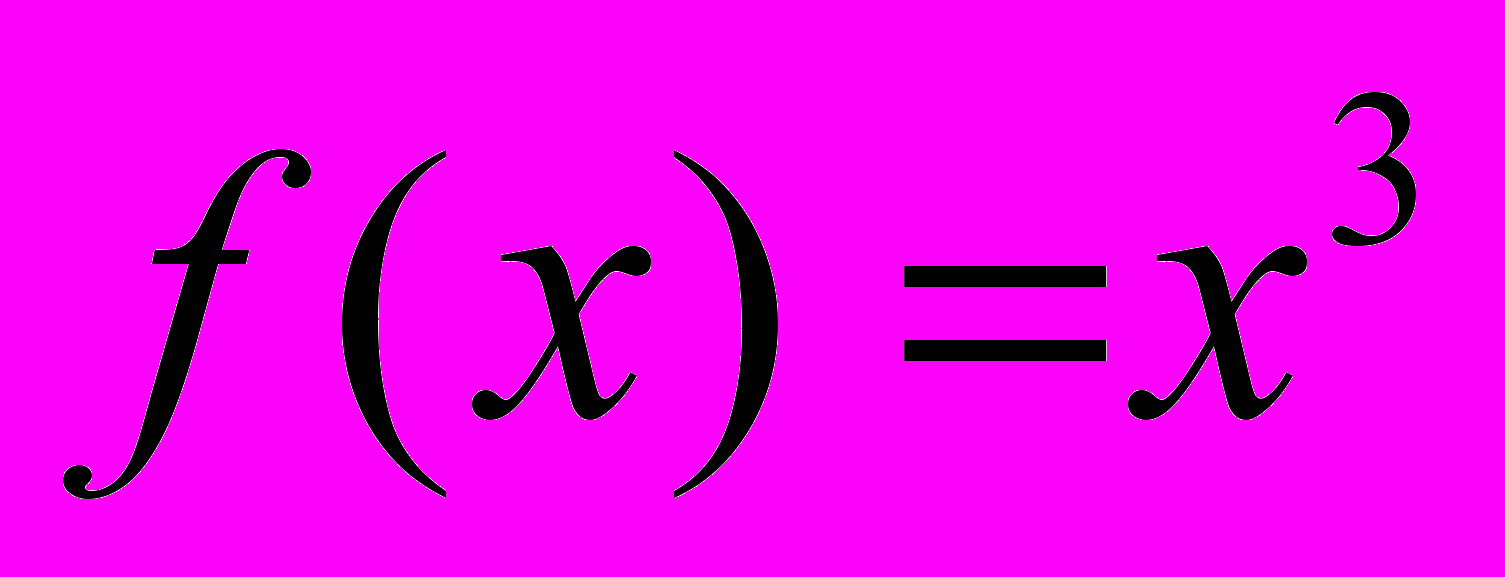
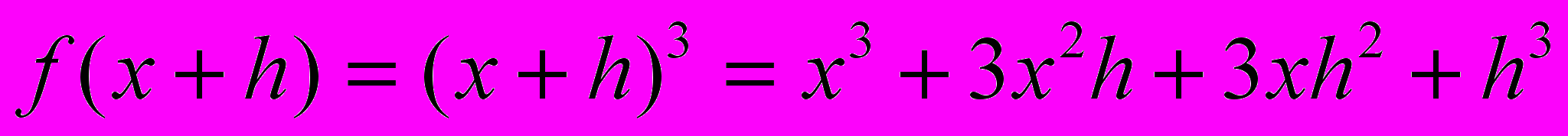
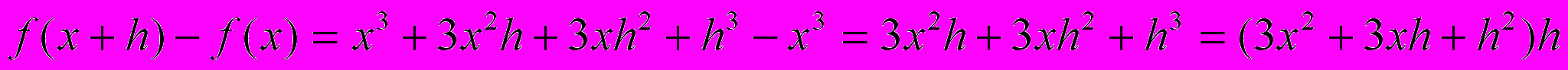
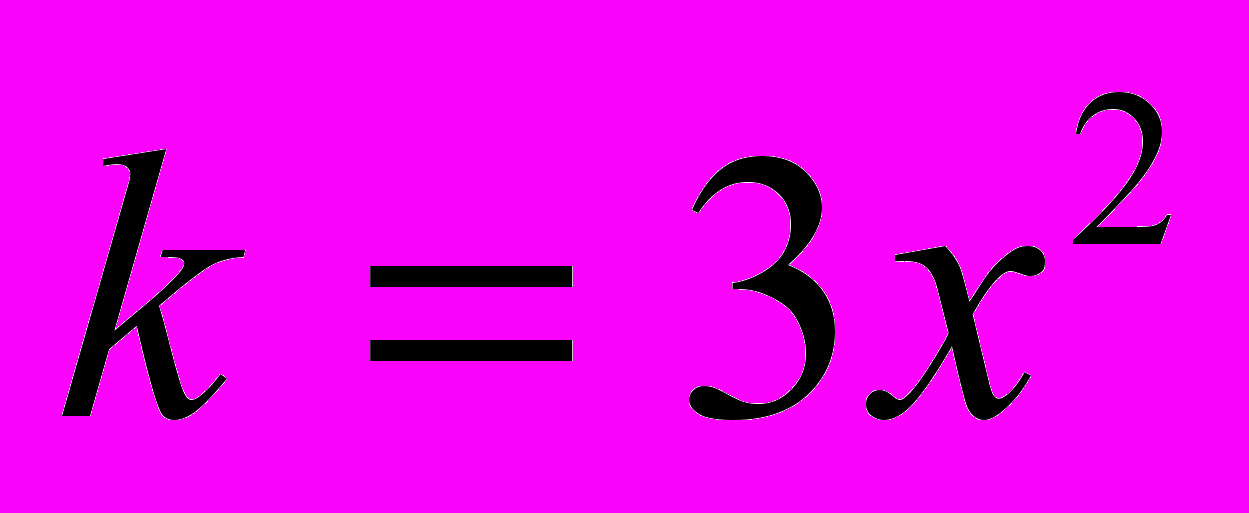 ;
;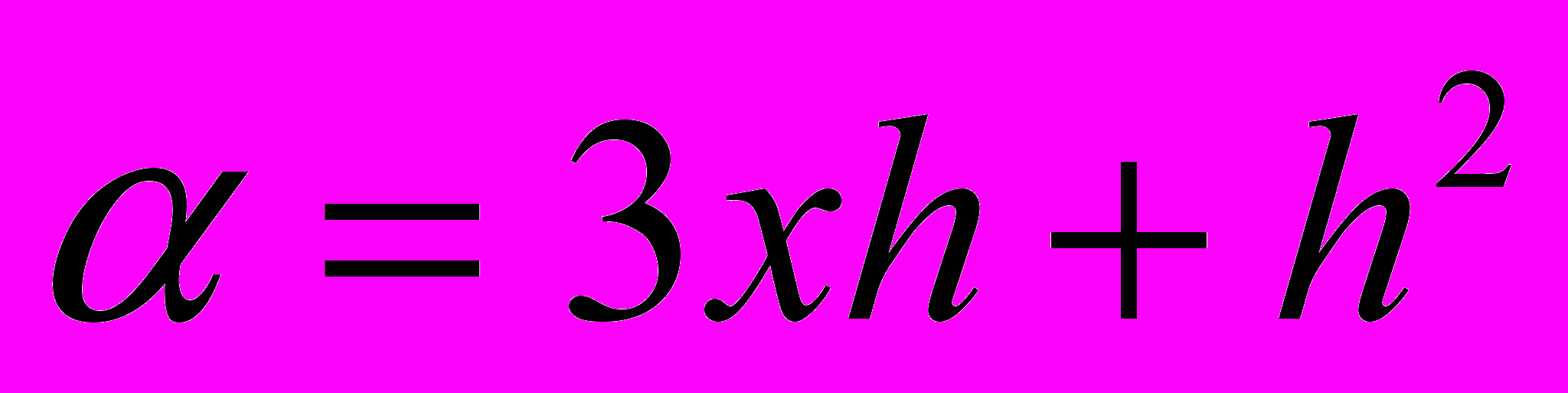 ;
;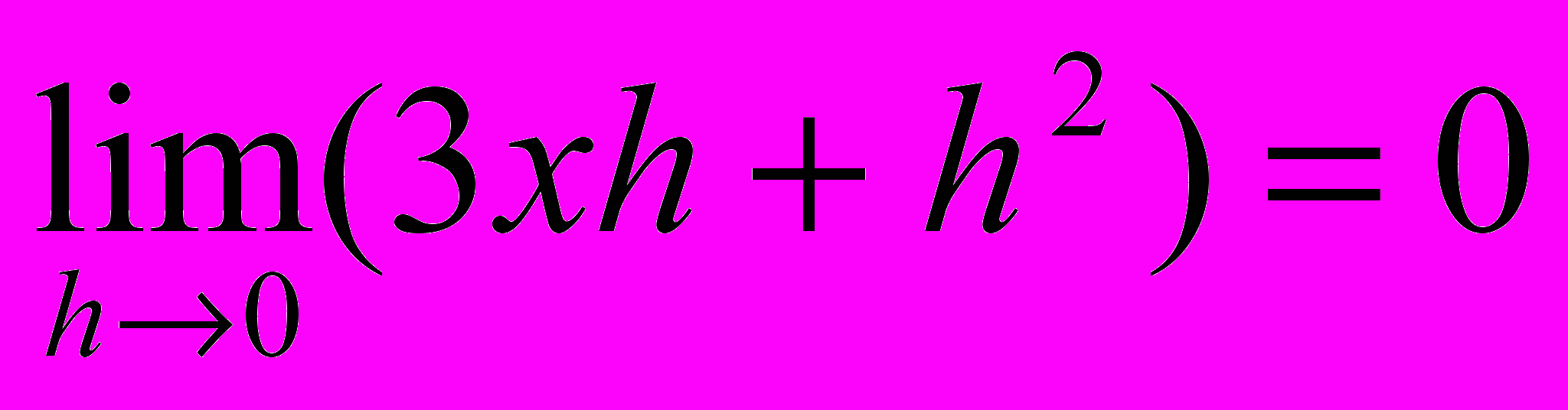
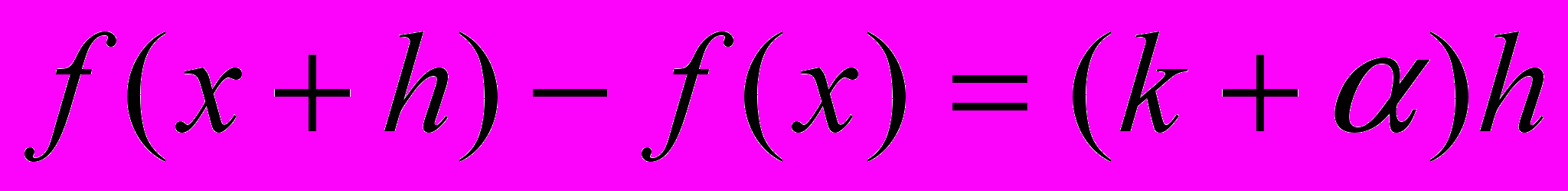
То есть функция y=x3 дифференцируема при любых значениях х.
IV. Производная.
Если функция дифференцируема, то её приращение можно записать в виде:
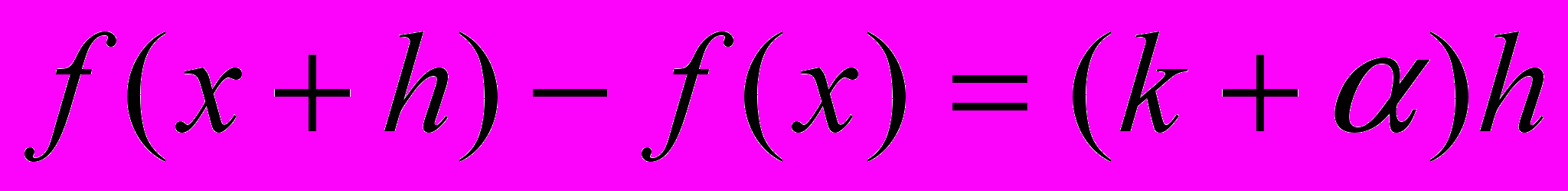
Выразим из этого равенства k:
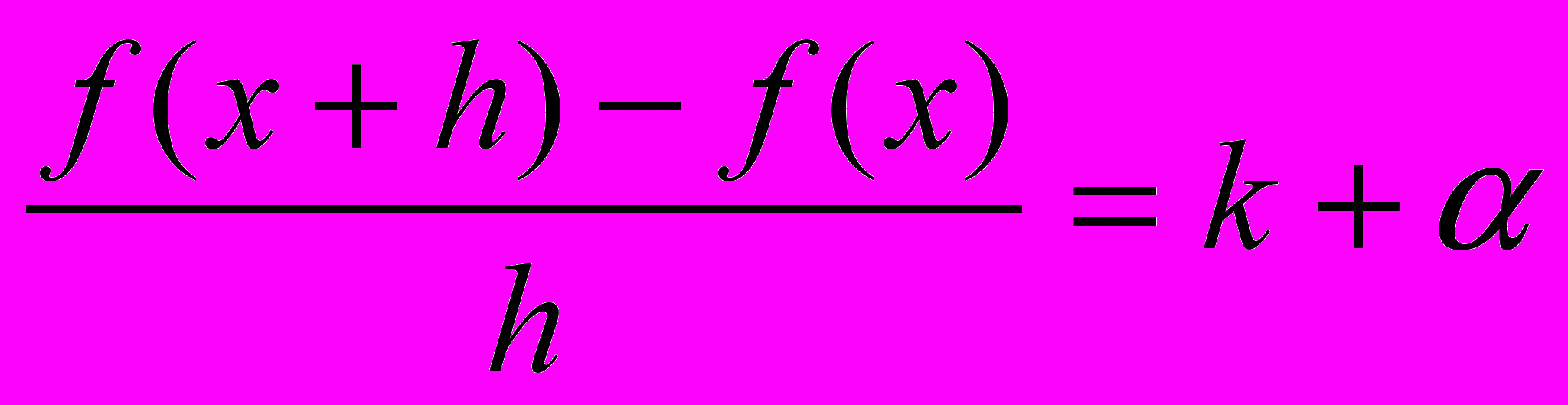 ,
, Но α→0 при h→0, следовательно,
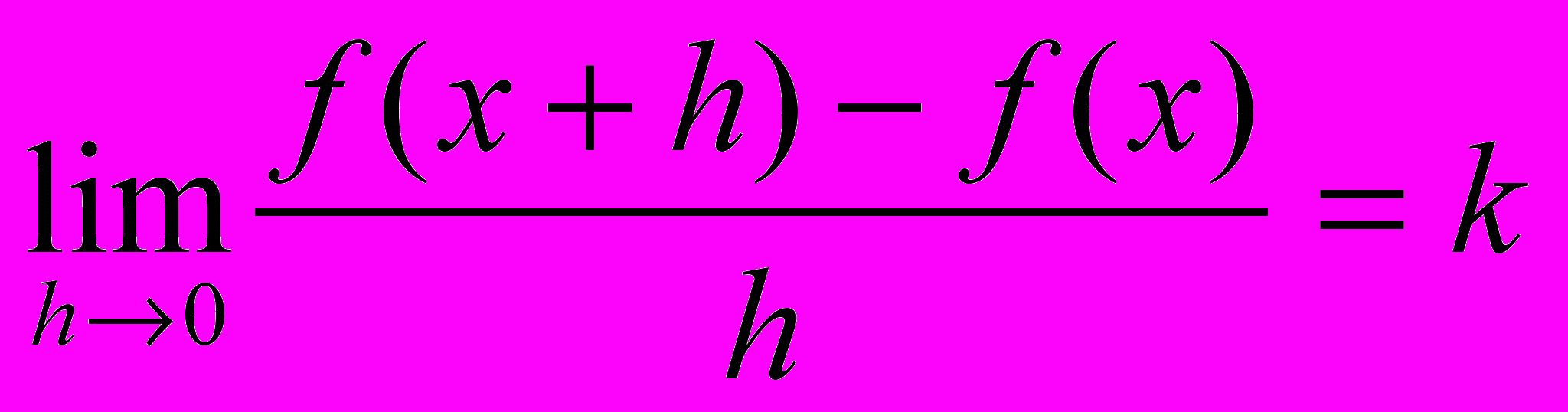 .
.Справедливо и обратное утверждение.
Итак, мы доказали теорему:
| Теорема: | Функция f дифференцируема в точке х в том и только в том случае, когда существует предел 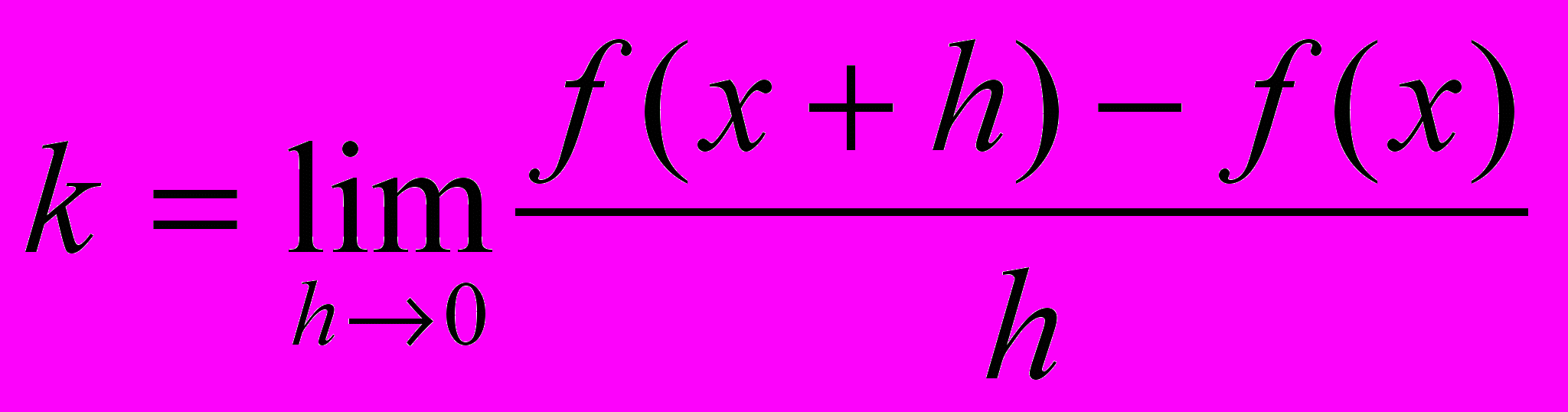 (1) (1)В этом случае 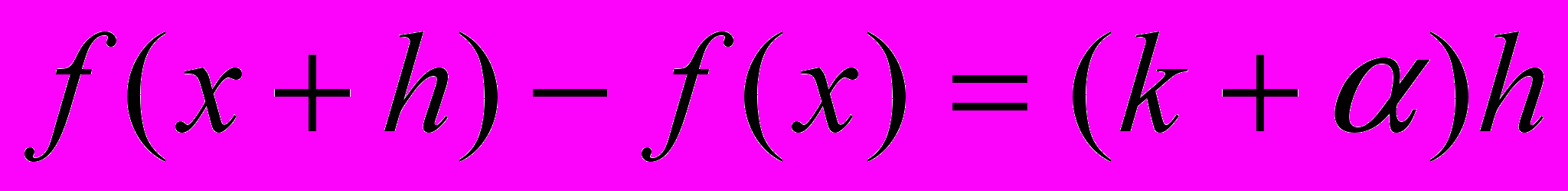 , где , где 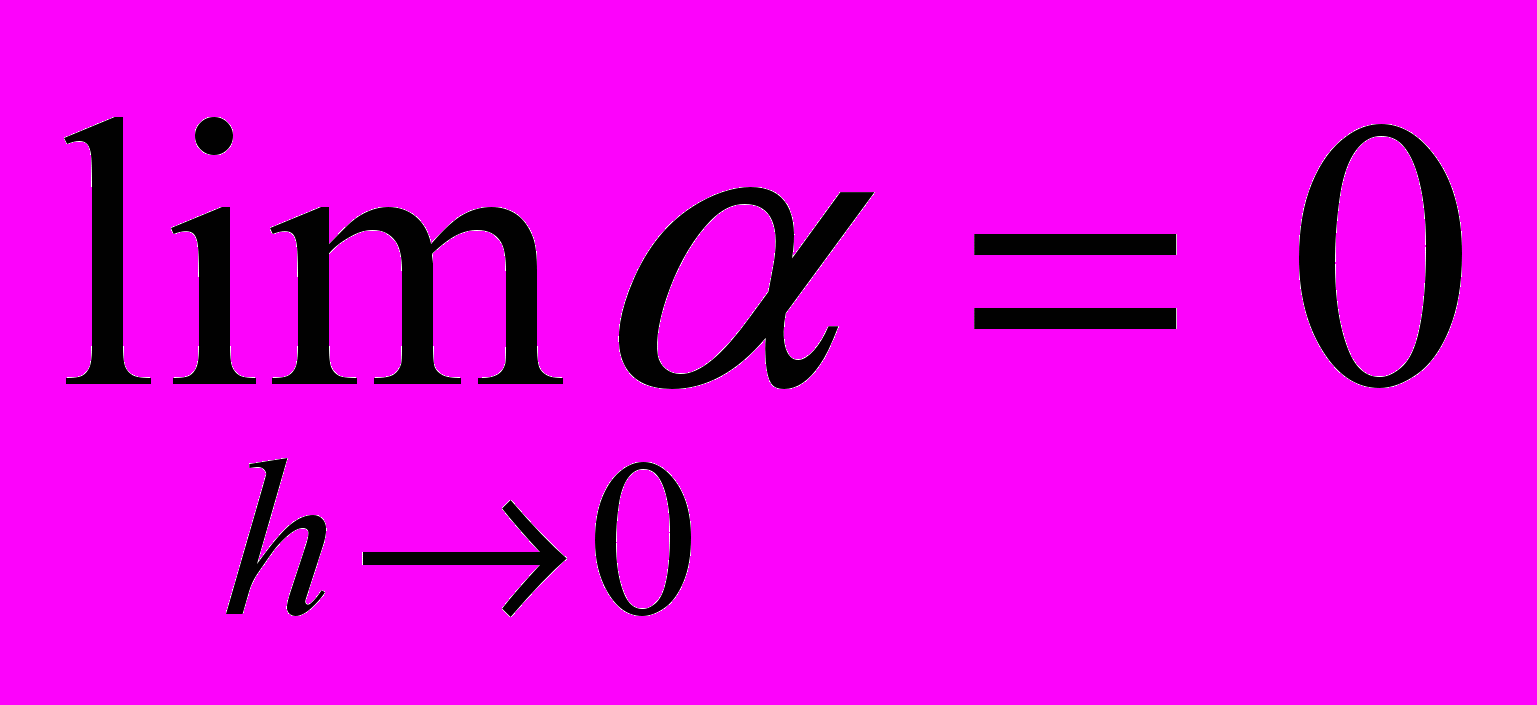 . . |
Значение k, даваемое формулой (1), зависит от выбора х. Поэтому, если функция f дифференцируема во всех точках промежутка Х, то каждому значению х из Х соответствует своё значение k. Этим определяется новая функция на Х, которую называют производной от функции f и обозначают f′.
| Определение: | Производной функции f называется функция f′, значение которой в точке х выражается формулой 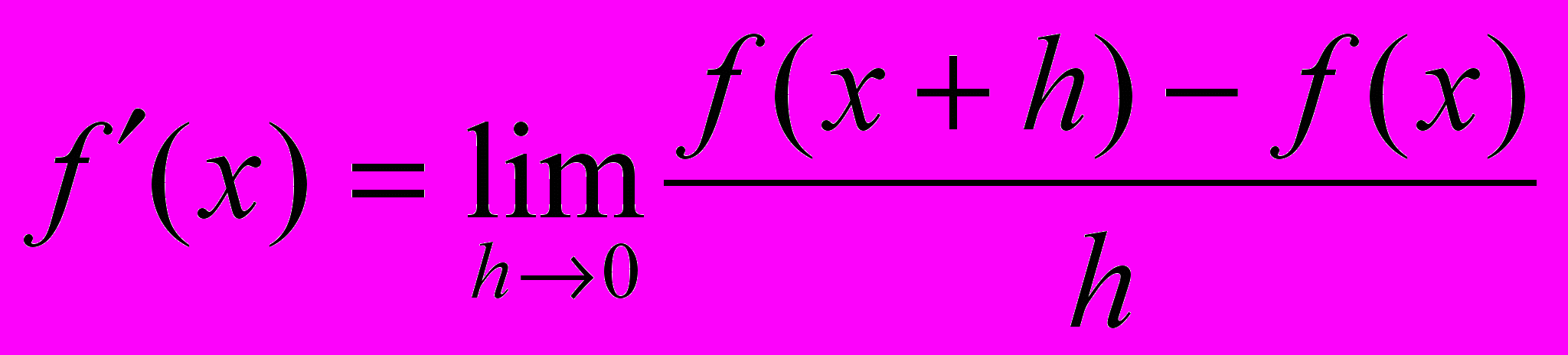 . . |
Значение производной от функции f в точке х равно пределу отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
| Пример 4. | Найти производную функции 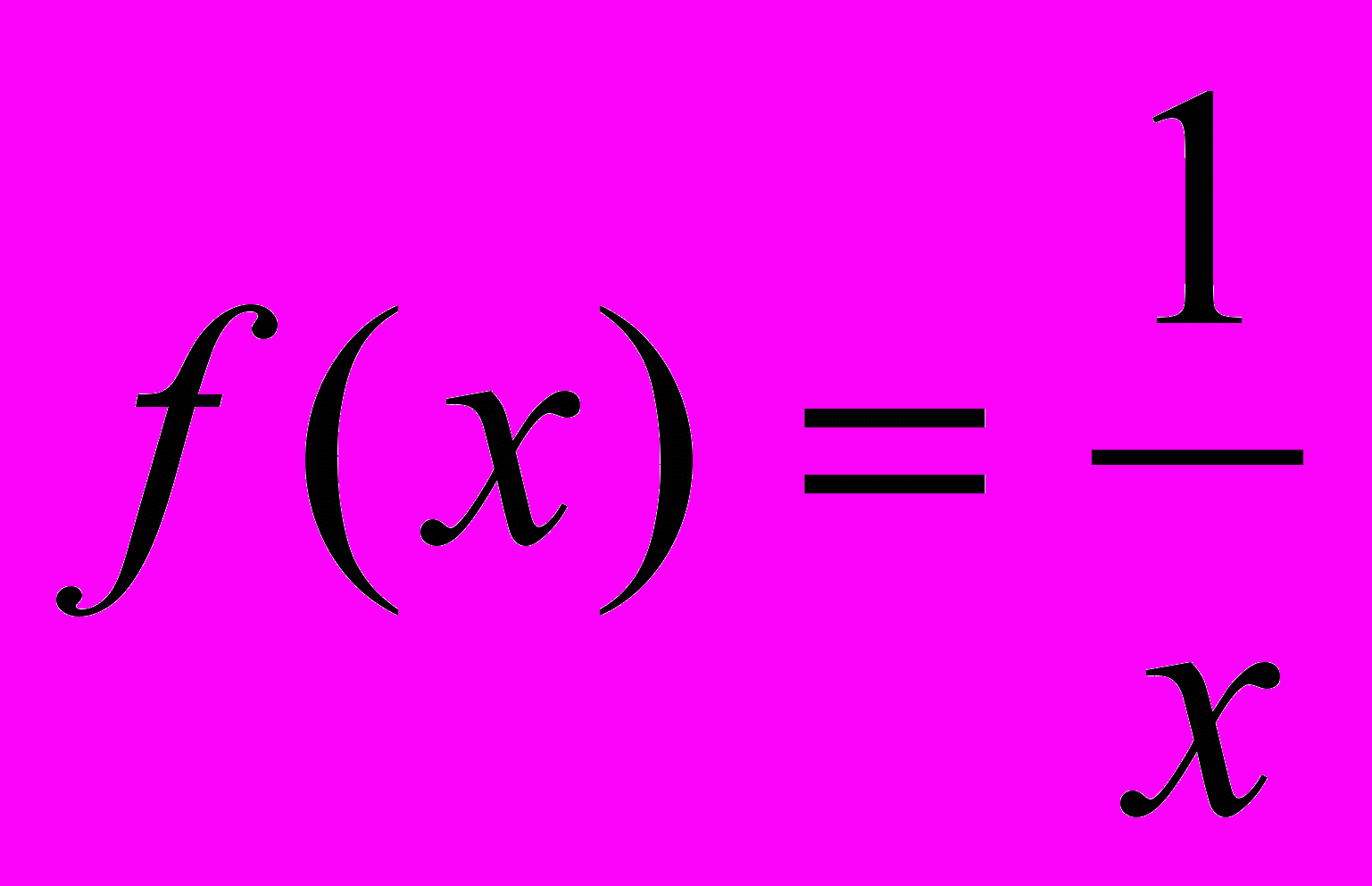 . . |
Решение.
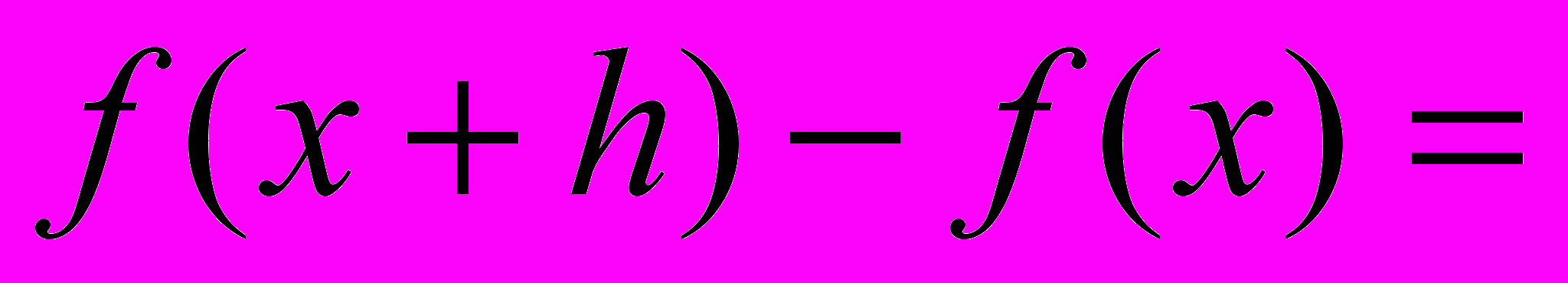
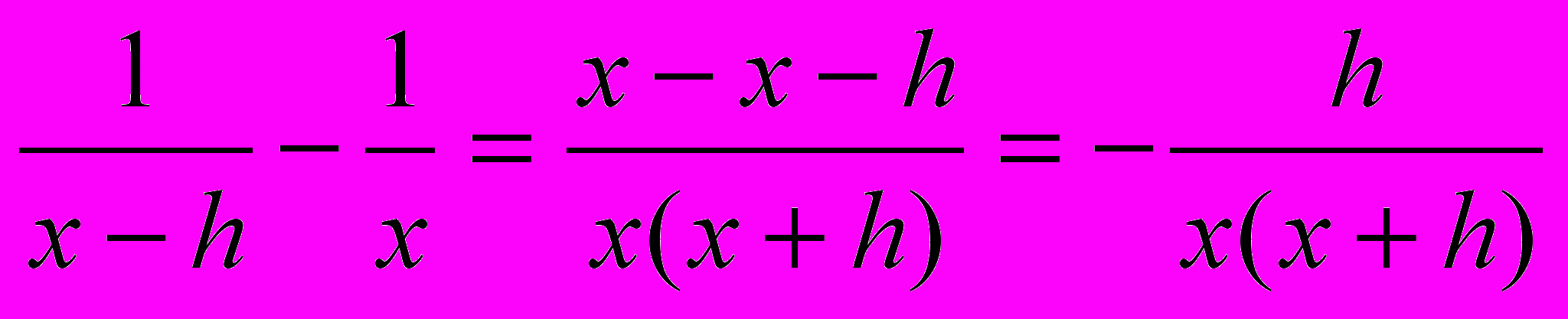
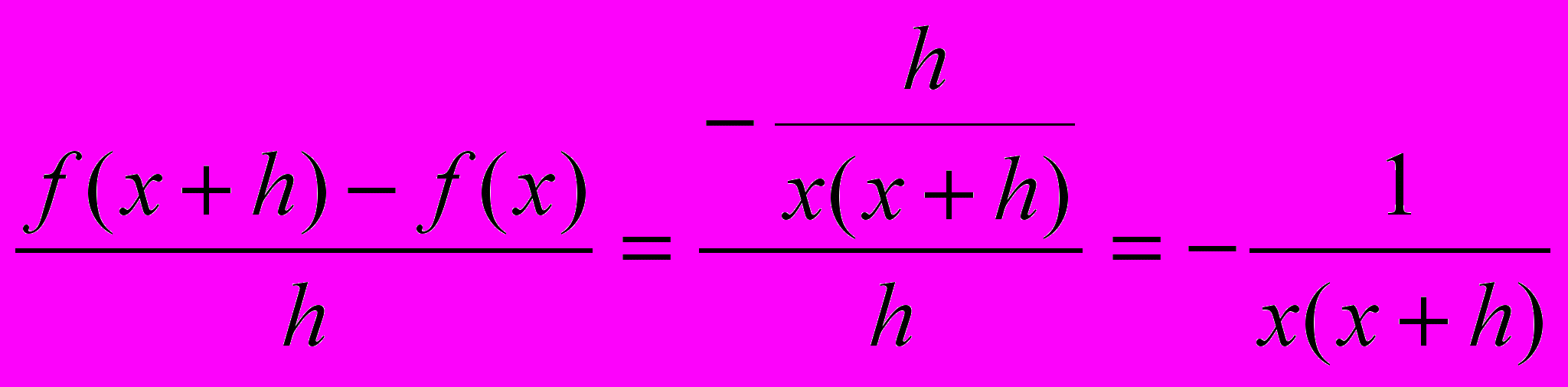
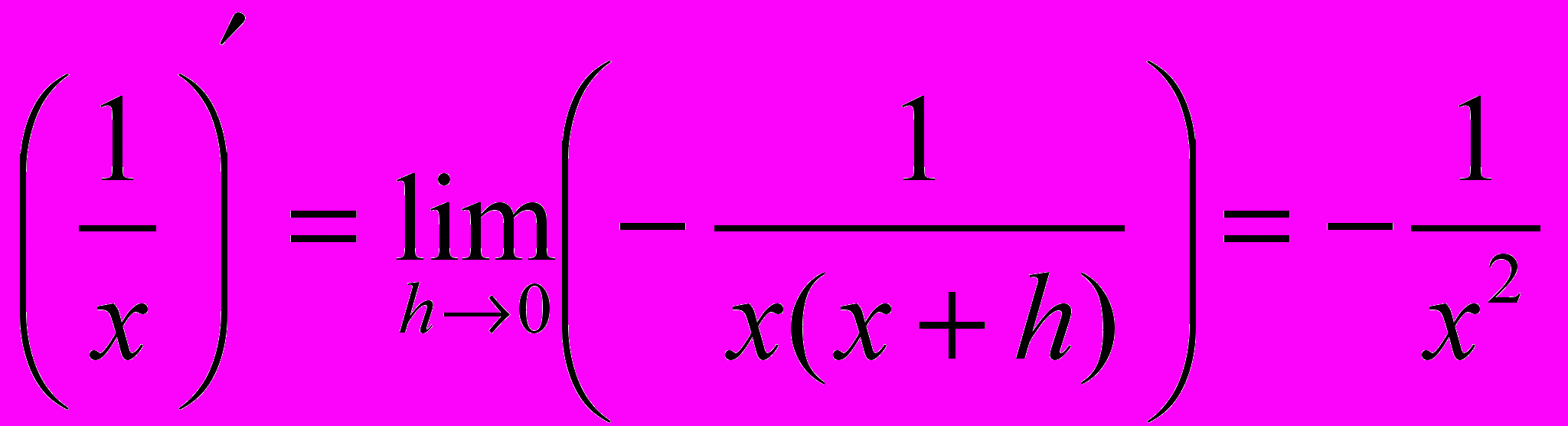 ;
;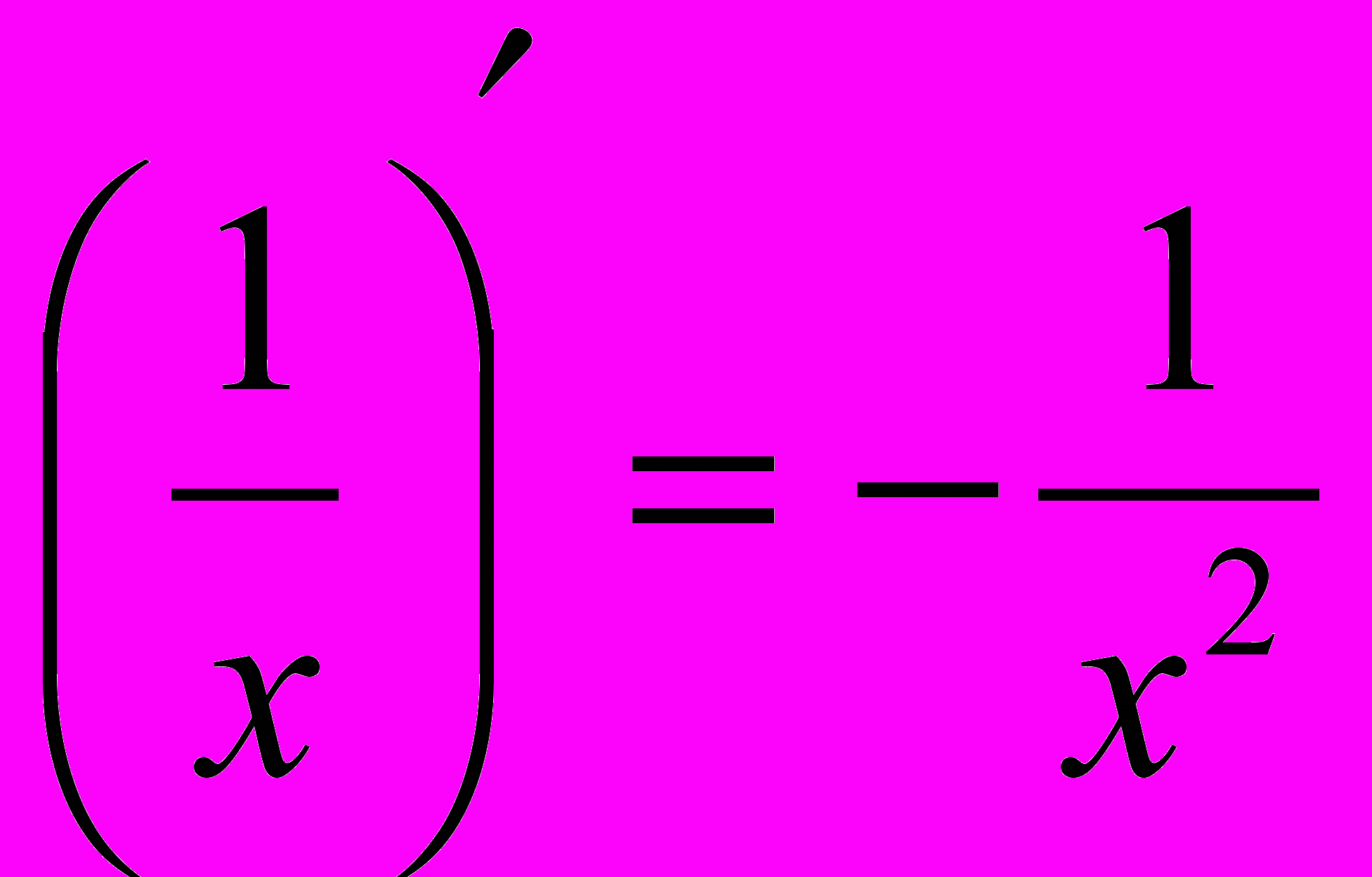 .
.Следующий пример выполняется учащимися самостоятельно в классе.
| Пример 5. | Найти производную функции 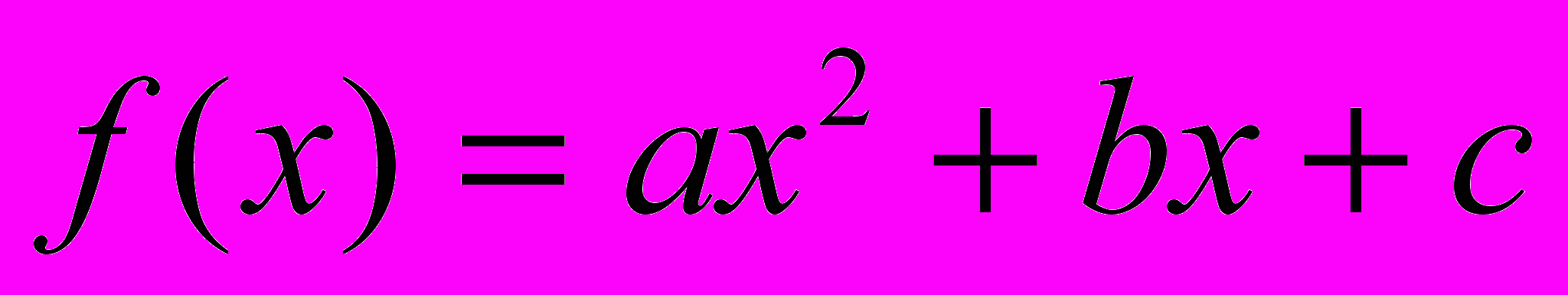 . . |
Решение.
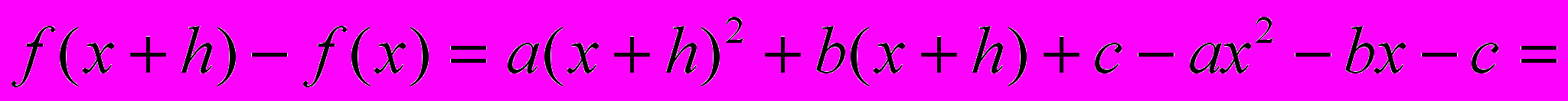
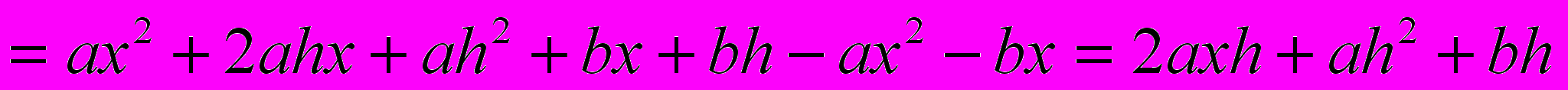
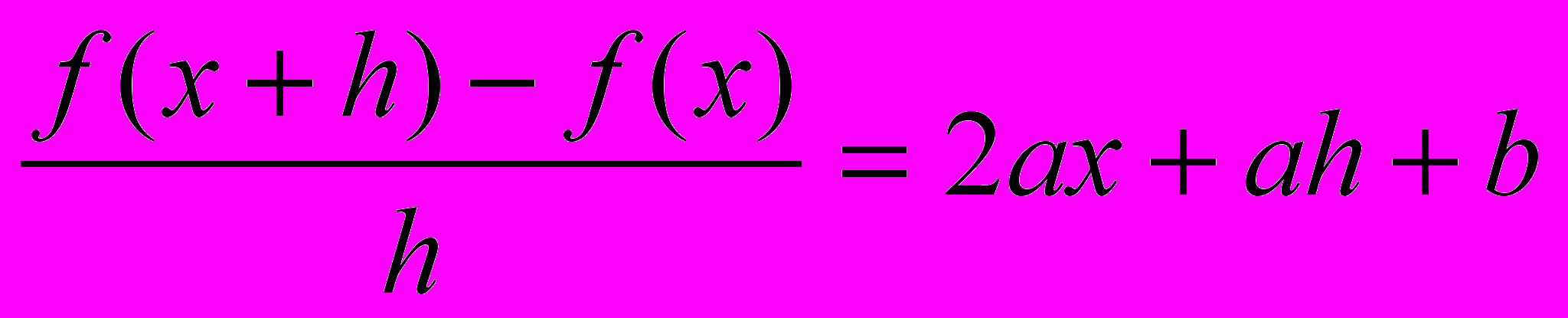
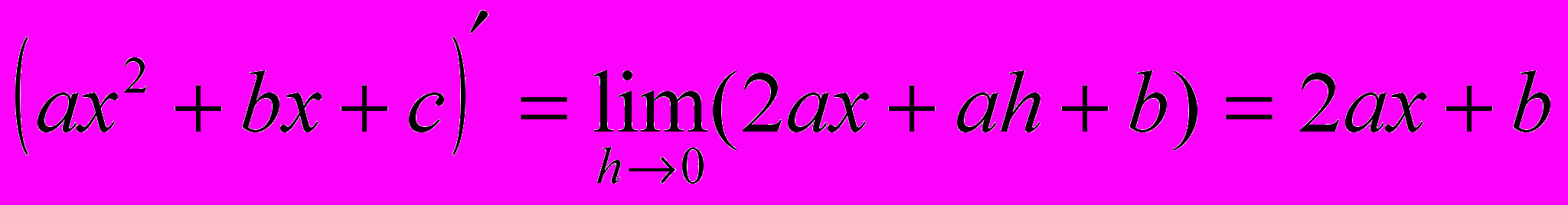
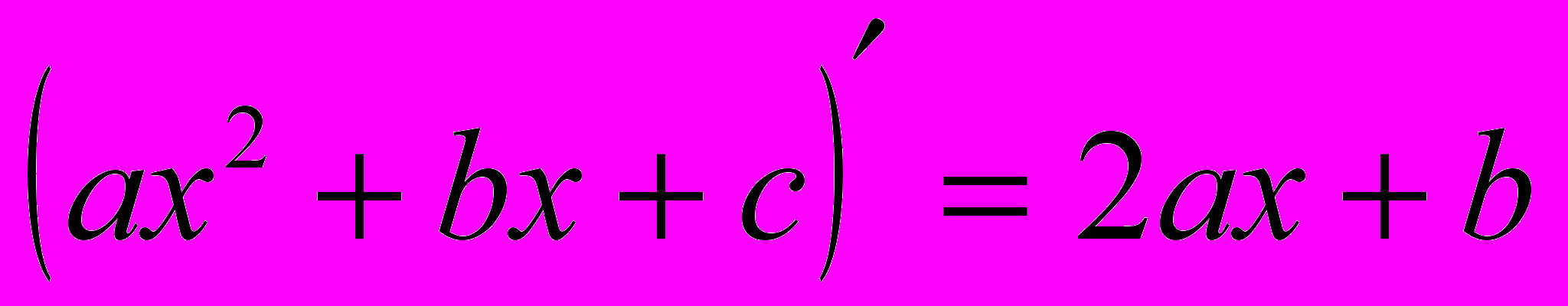
^ V. Дифференциал.
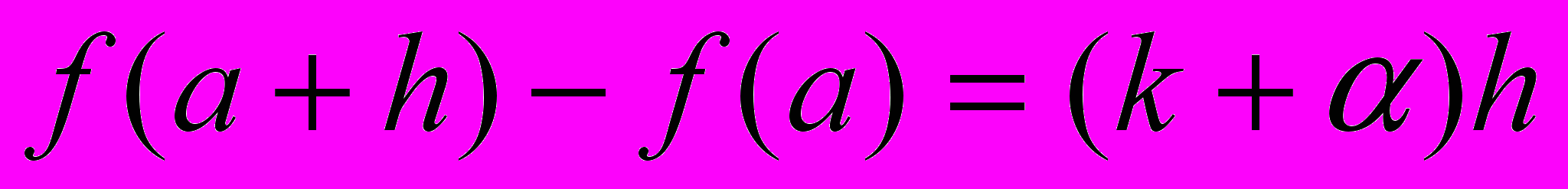 (1)
(1)Мы знаем теперь, что
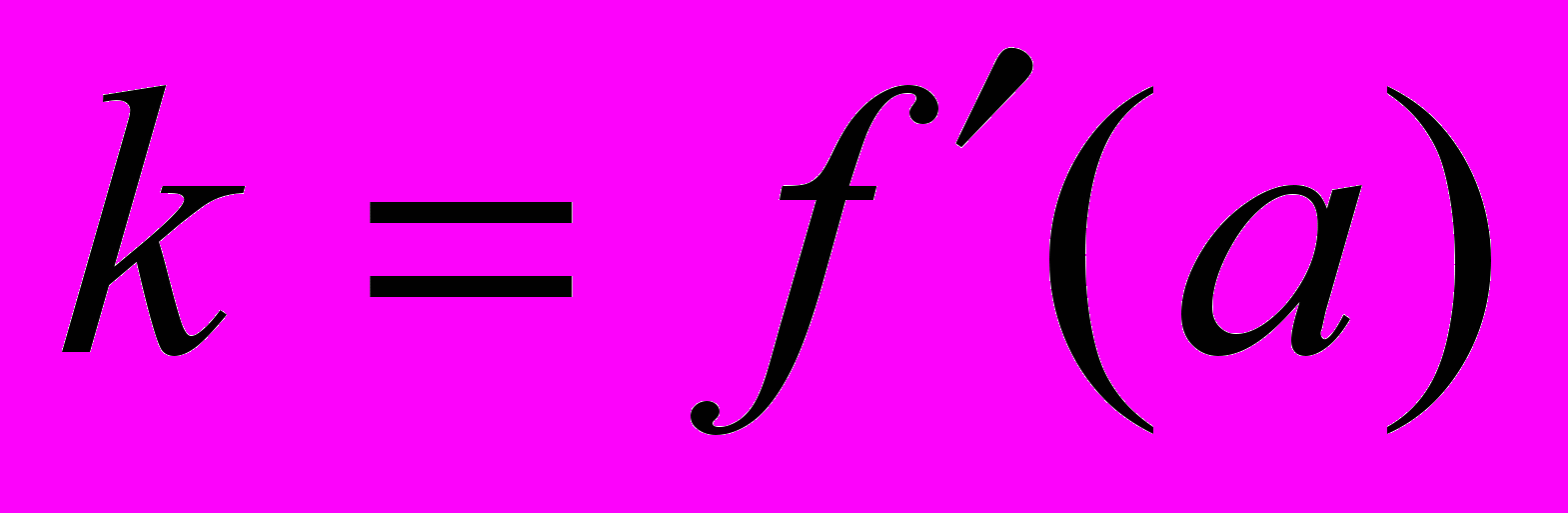 ,
, поэтому формулу (1) мы можем переписать в виде
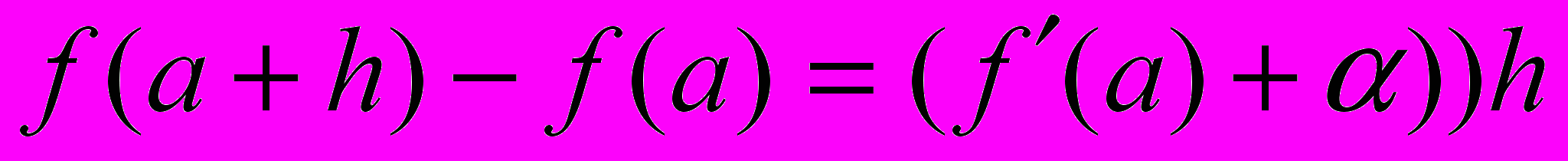
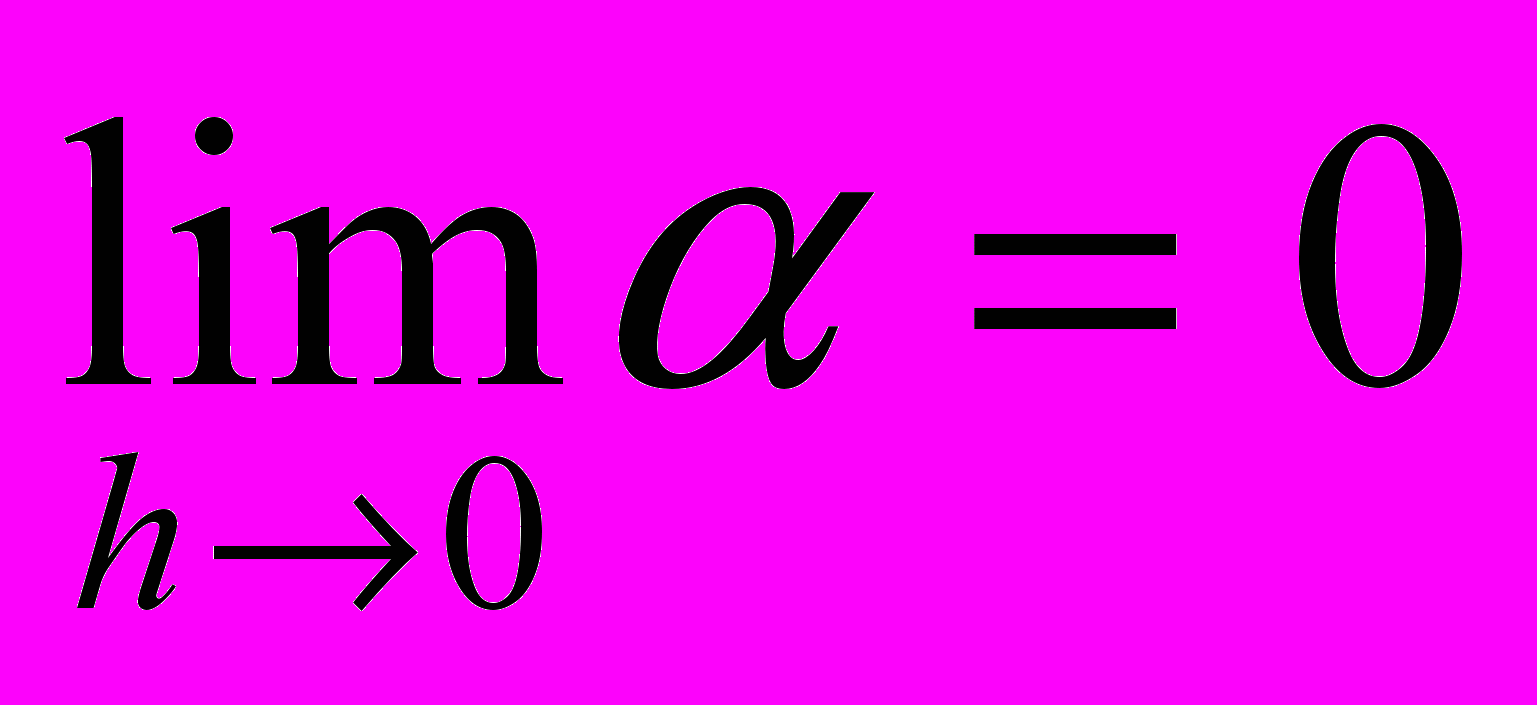
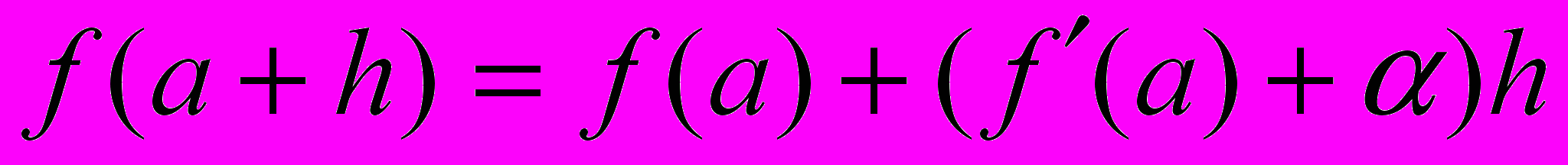
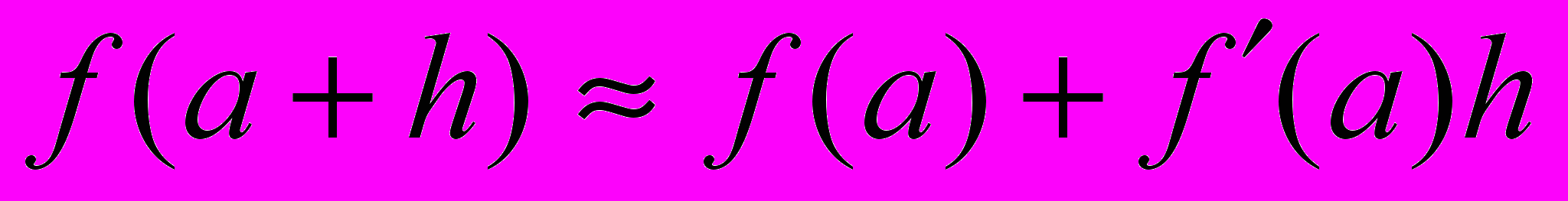 (2)
(2)Равенство (2) применяется для приближённого вычисления значений функции f вблизи точки а.
| Пример 6. | Найти значение функции 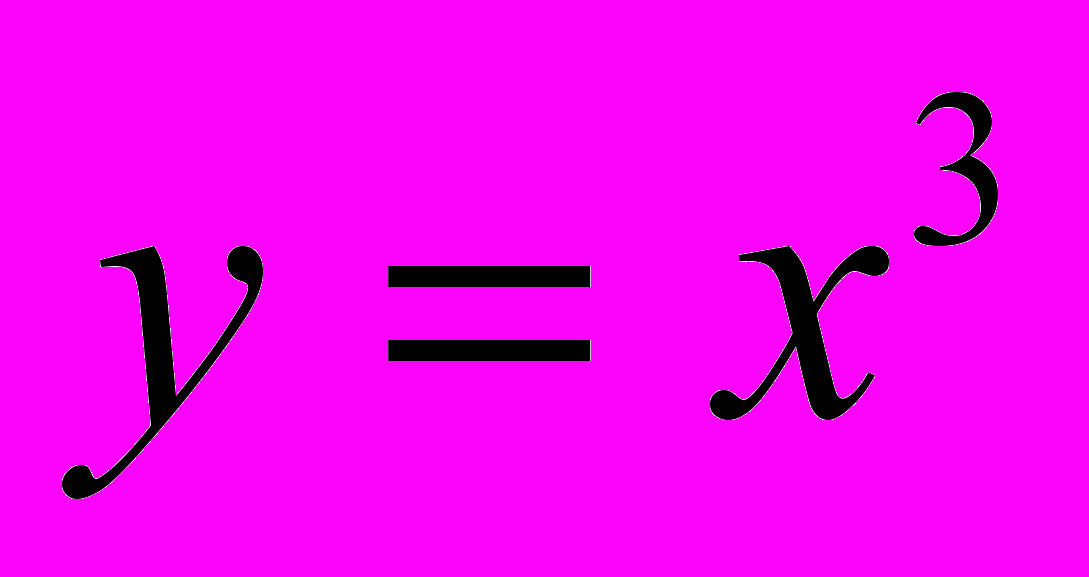 при при 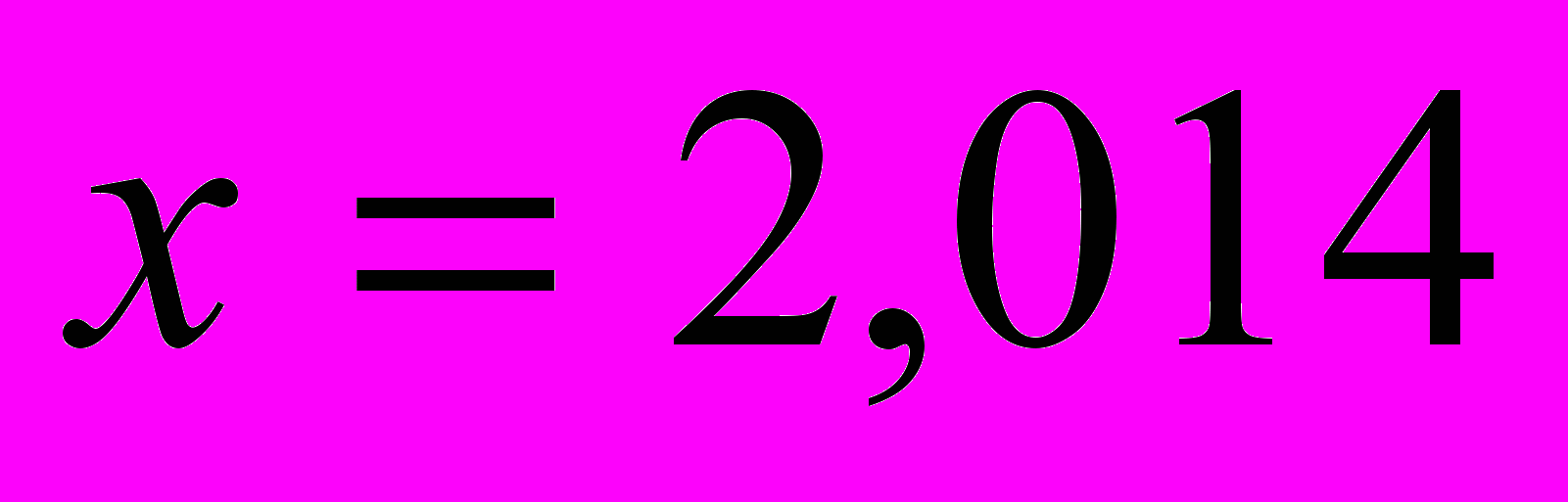 с точностью до с точностью до 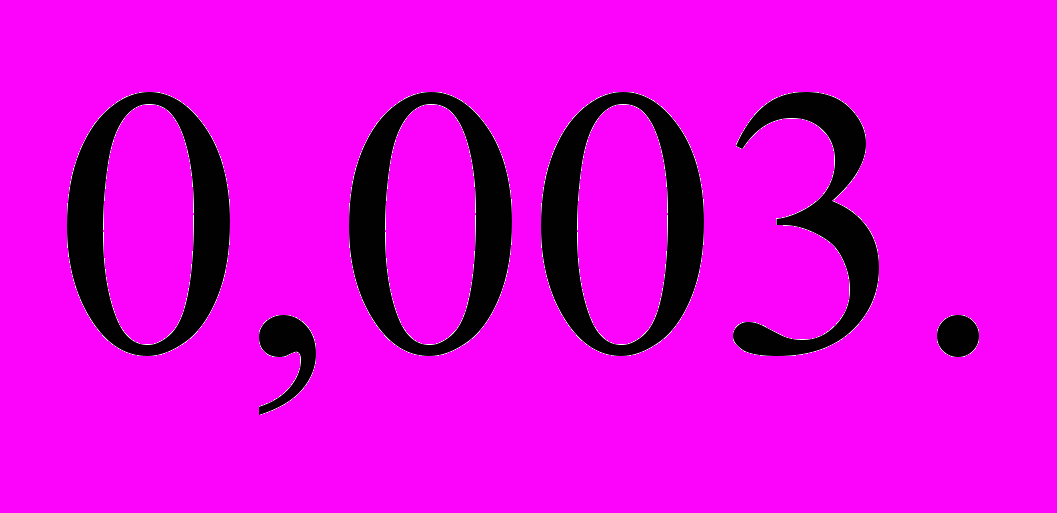 |
Решение.
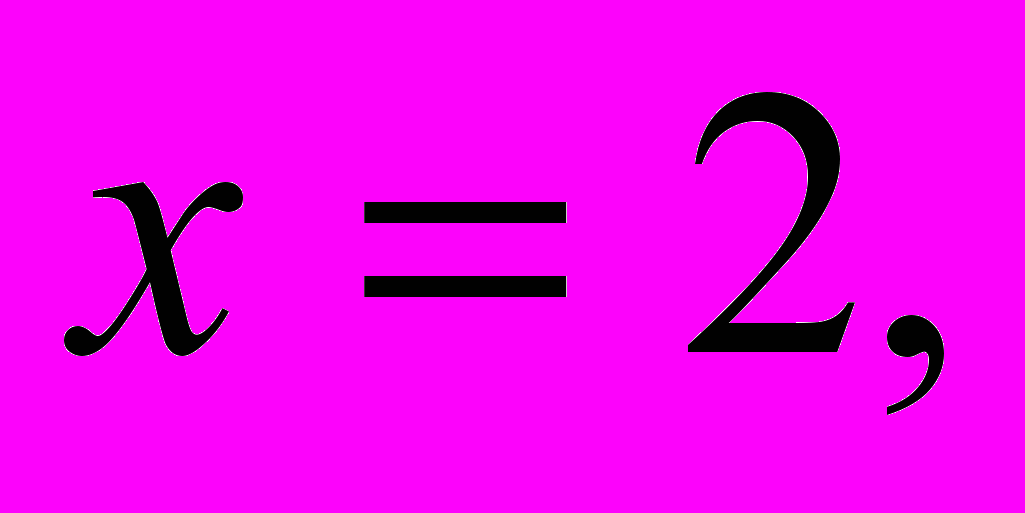
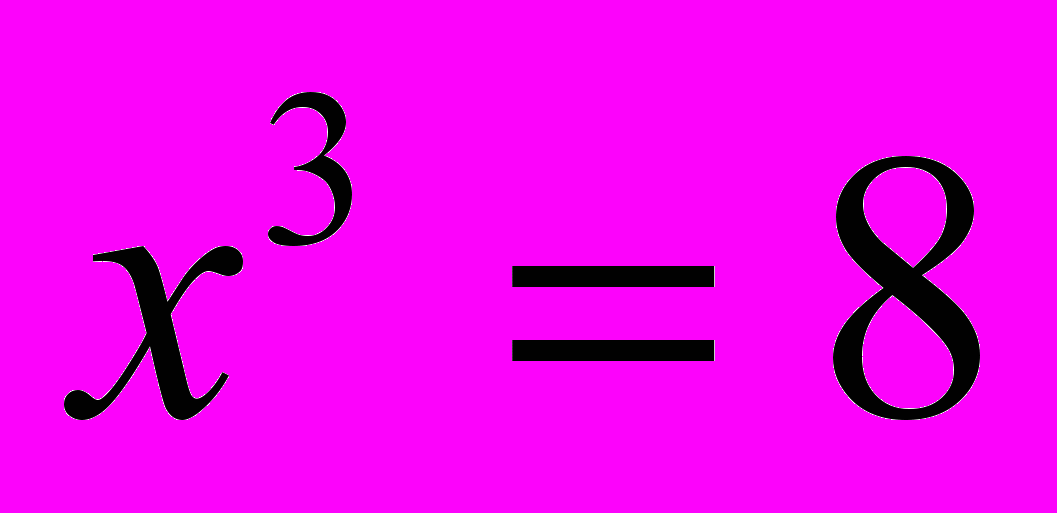
Производная этой функции равна
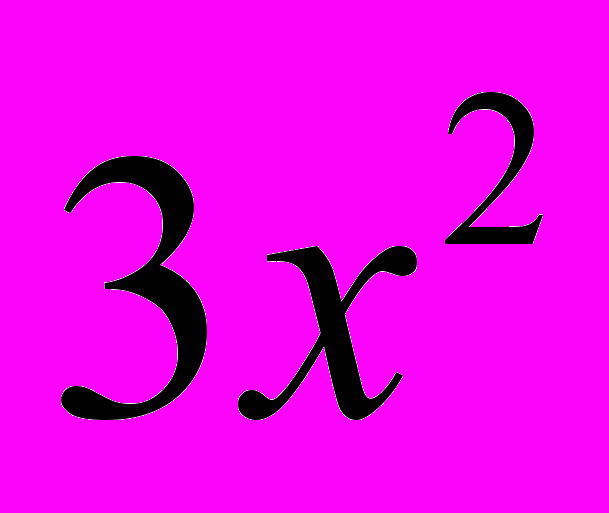 и следовательно её значение
и следовательно её значение 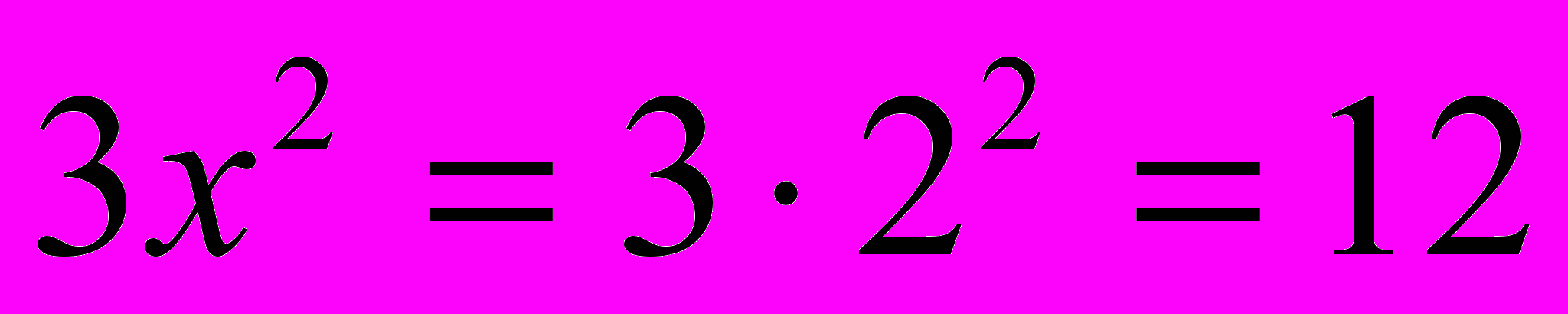 .
.Итак, если
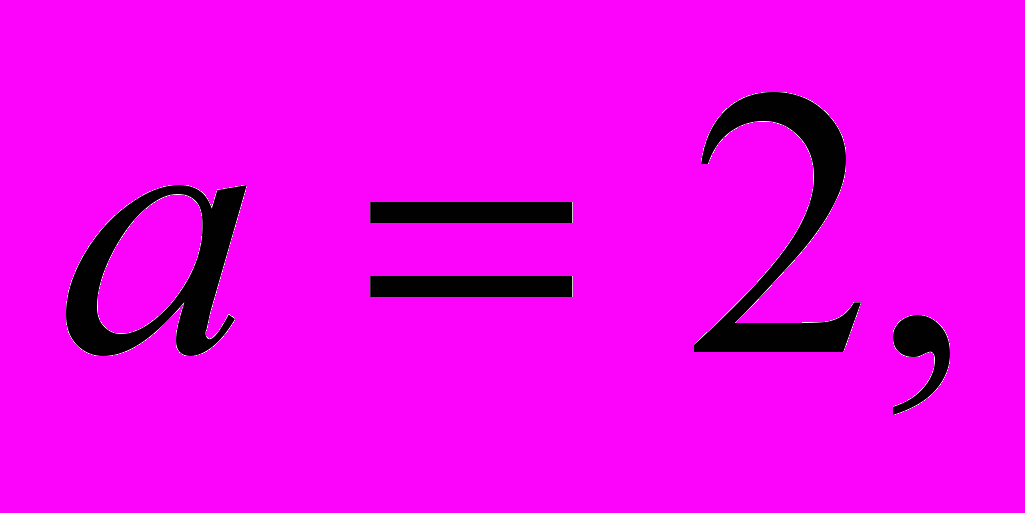 то
то 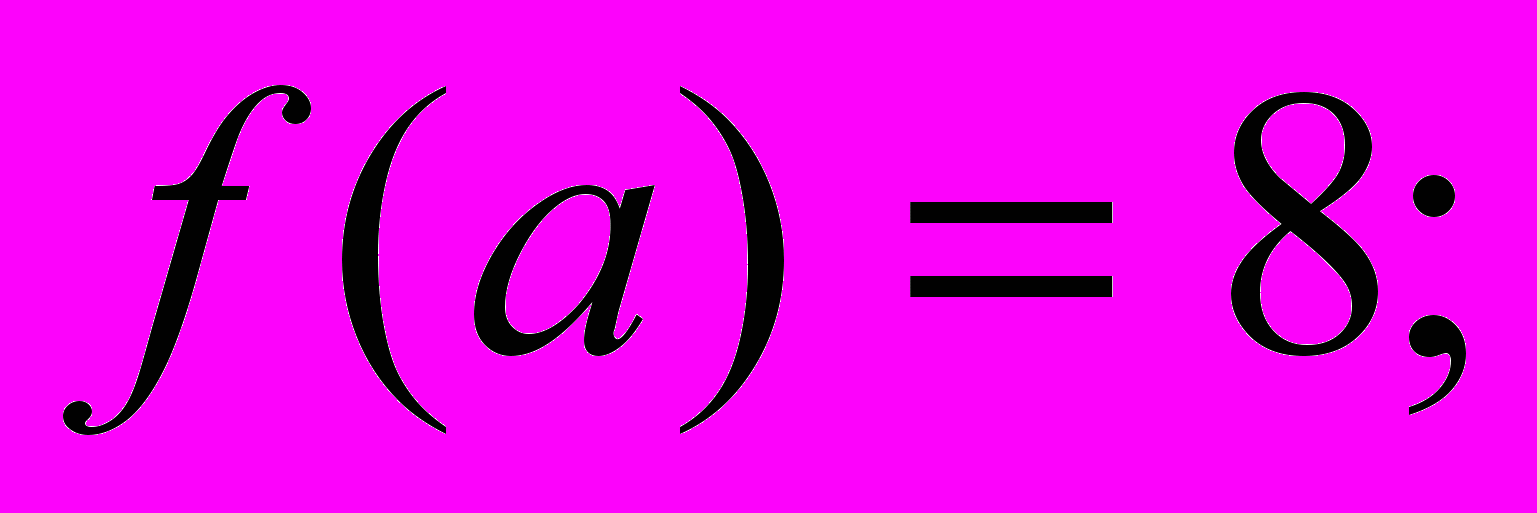
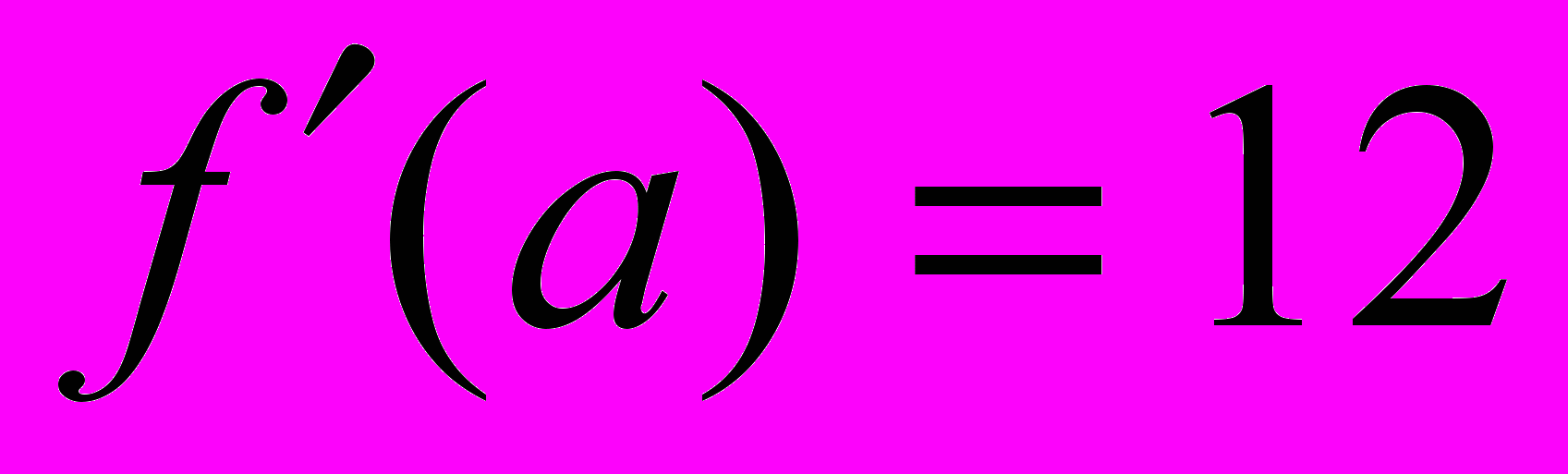 и
и 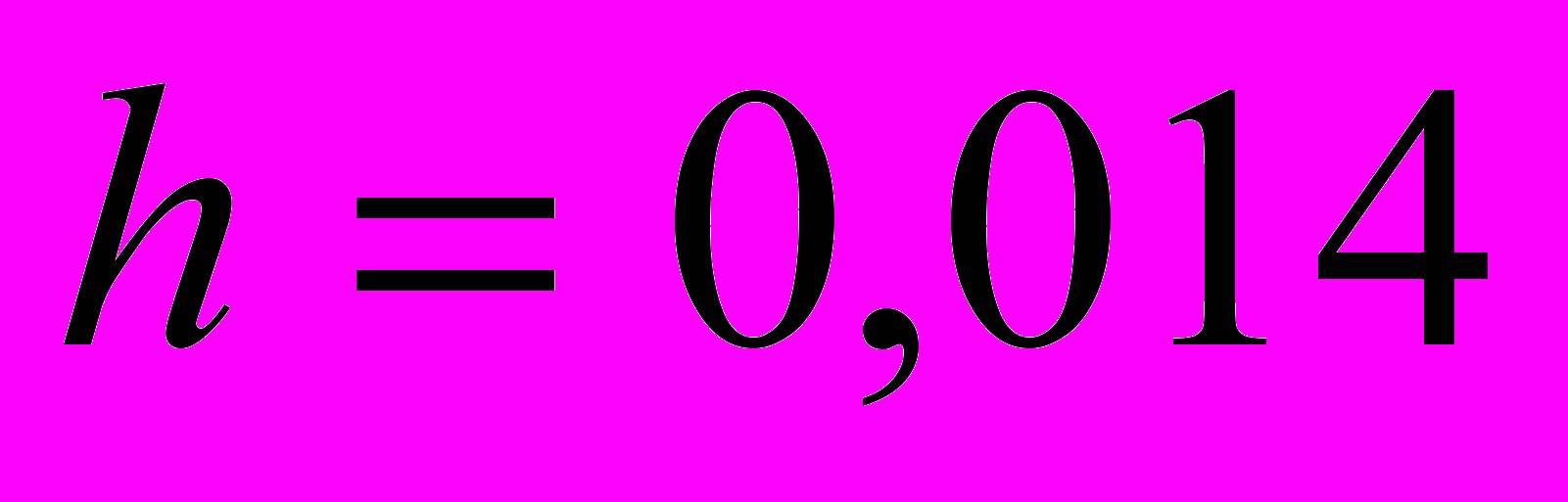
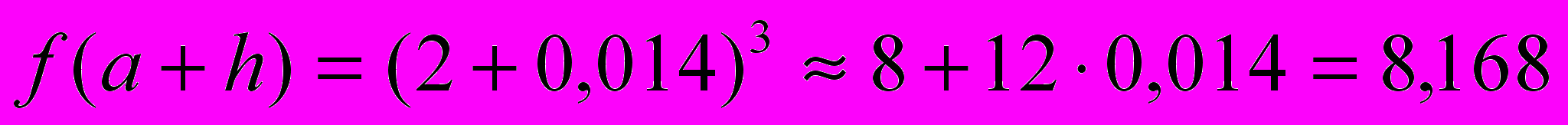
Погрешность полученного значения равна
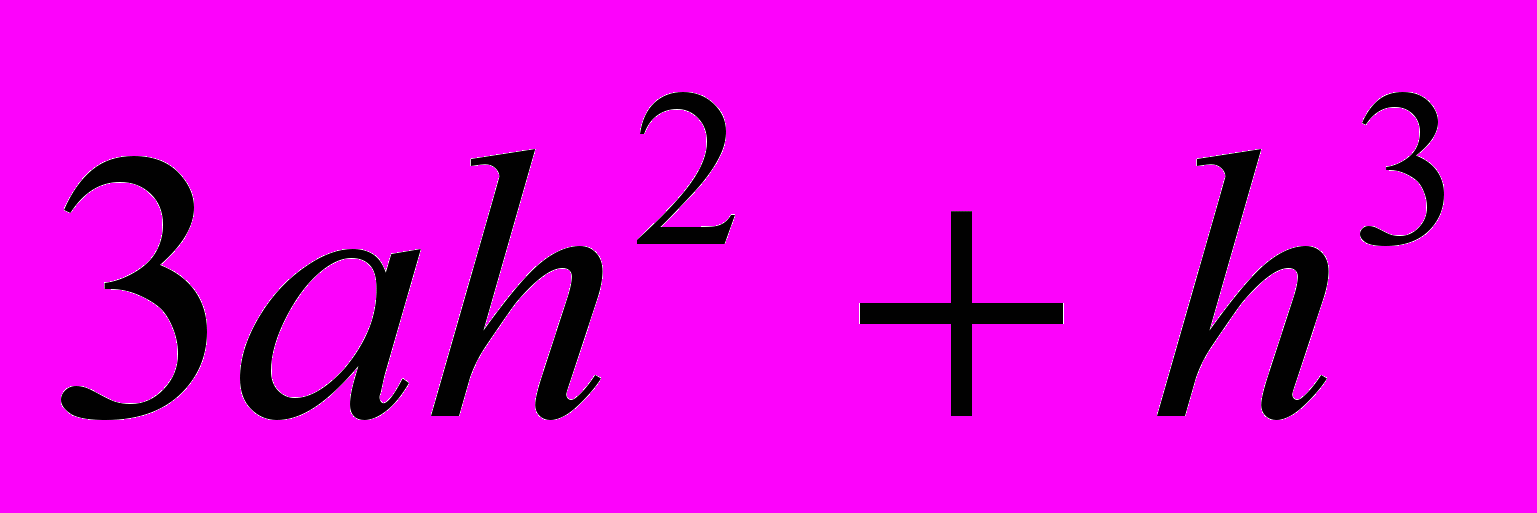 , то есть
, то есть 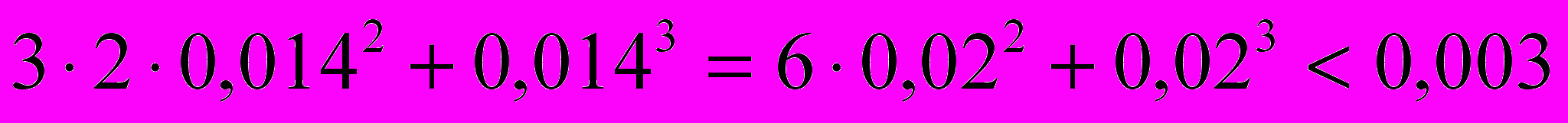 , так как
, так как 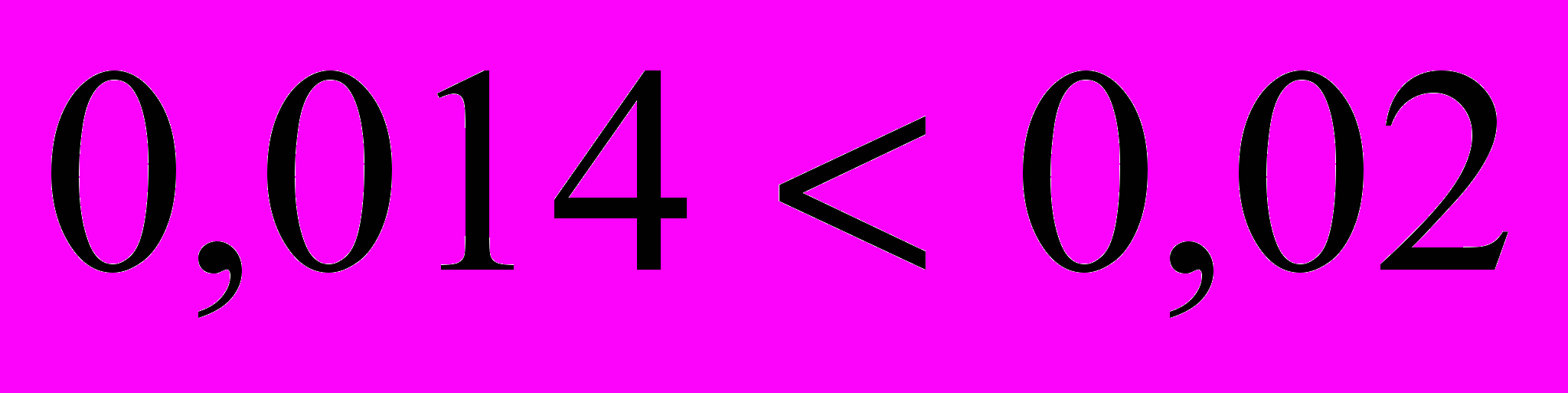 .
.Имеем:
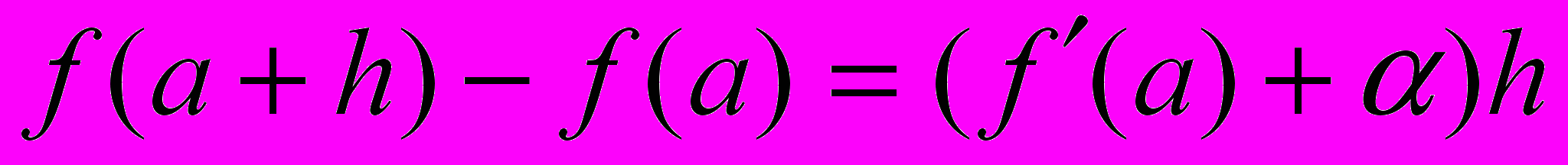 ;
; 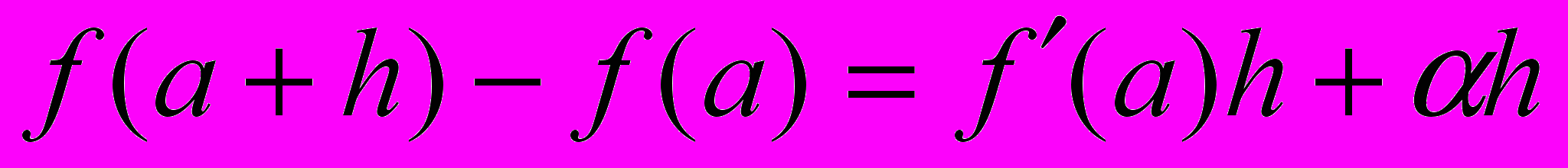 .
.Приращение функции состоит из двух слагаемых.
Слагаемое
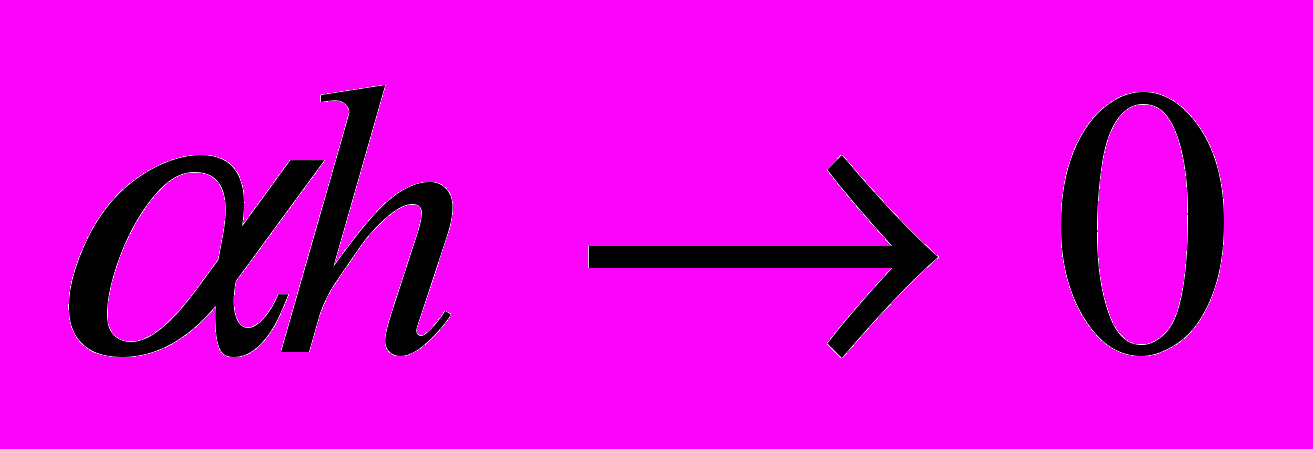 , а слагаемое
, а слагаемое 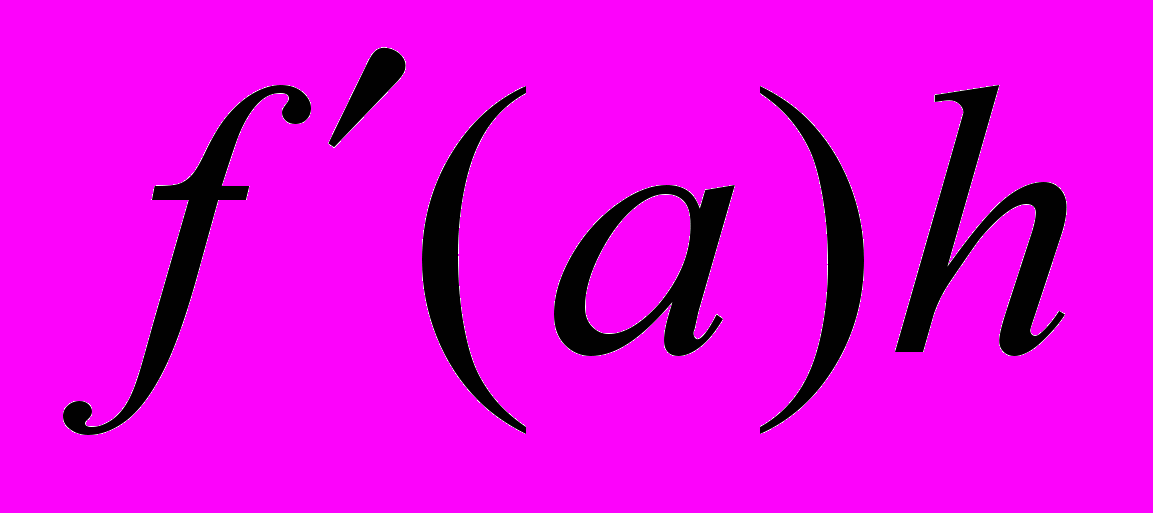 называют дифференциалом функции и обозначают
называют дифференциалом функции и обозначают  .
.Таким образом,
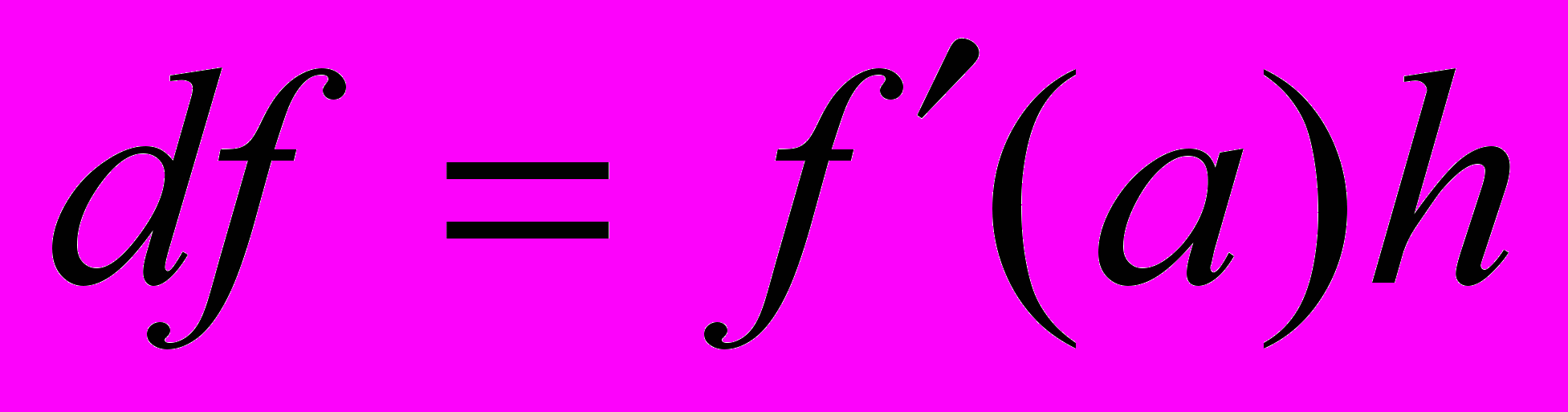
Домашнее задание: №380 (1, 2); №390 (а); №392 (1, 2, 3); №397 (а, б).
