Состав научно-образовательного коллектива (основные исполнители)

Вид материала

Документы

Содержание Ключевыми понятиями Область применения Образовательная программа.

Подобный материал:

• «Менеджер социальной сферы» Состав научно-образовательного коллектива (основные исполнители), 220.11kb.
• «Менеджер по управлению персоналом» Состав научно-образовательного коллектива (основные, 269.59kb.
• «Специалист по организации работы с молодежью и семейной политике» Состав научно-образовательного, 300.32kb.
• «Организация и проведение профессиональной переподготовки «Менеджер организации и реабилитации, 280.94kb.
• Научно-образовательный материал Организация курсов повышения квалификации «Квалиметрические, 218.34kb.
• «Организация и проведение профессиональной переподготовки «Менеджер образования» Состав, 358.39kb.
• Разработка и апробация программы повышения квалификации по теме «Информационные технологии, 155.64kb.
• Разработка и апробация программы повышения квалификации «Информационные технологии, 196.83kb.
• Разработка и апробация программы повышения квалификации по теме «Информационные технологии, 157.01kb.
• Основные сведения, 138.18kb.

Некоммерческая организация «Ассоциация московских вузов»

ФГБОУ ВПО «Российский государственный социальный университет»


Научно-образовательный материал


«Разработка и апробация серии электронных образовательных ресурсов по математике»


Состав научно-образовательного коллектива (основные исполнители):


Жукова Г. С. д.ф.-м.н., профессор, проректор по дополнительному профессиональному образованию, повышению квалификации и переподготовке кадров

Комарова Е. В. к.ф.-.м.н., доцент, доцент кафедры математики и информатики

Панфилов В. И. д.т.н., профессор, профессор кафедры математики и информатики

Семеновых Д.Н. к.ф.-.м.н., доцент, доцент кафедры математики и информатики

Чахкиев М.А. д.ф.-м.н., профессор, профессор кафедры математики и информатики

Елагин К.В. специалист по УМР 1 кат.


Москва 2011 г.

Для качественной подготовки и переподготовки специалистов в области управления малым предприятием необходимо наличие современных учебно-методических программ и материалов. Разработка специального пакета прикладных программных продуктов по формированию плана производства и стратегий поведения на рынке в условиях конкуренции для предприятий малого и среднего бизнеса столичного мегаполиса позволит повысить качество подготовки указанных специалистов.

В результате анализа современных математических методов для создания пакета прикладных программных продуктов были предложены:

1. Методы линейного программирования для создания программного модуля «Формирование плана выпуска продукции»;
   
2. Методы целочисленного программирования для создания программного модуля «Оптимизация плана выпуска продукции»;
   
3. Методы теории игр для создания программного модуля «Стратегия поведения в условиях конкуренции».
   

В ходе создания научно-образовательных материалов по направлению профессиональной переподготовки специалистов по управлению технологическими процессами предприятий и организаций, работающих в сфере производства и оказания услуг населению, столичного мегаполиса по дополнительной профессиональной образовательной программе «Разработка и апробация серии электронных образовательных ресурсов по математике» на основе модели компетенций менеджера по управлению технологическими процессами, Исполнителем в соответствии с утвержденным Техническим заданием разработан пакет научно-образовательных материалов, включающий в себя пакет прикладных программных продуктов и сопроводительную документацию, по подготовке менеджеров по управлению технологическими процессами.

Ключевыми понятиями исследования являются: профессиональная компетентность; математическая модель технологического процесса; система ограничений на ресурсы; оптимальный план выпуска продукции; ведущий элемент; критерий останова; стратегия поведения, седловая точка, критерии риска.

Цель научно-образовательной разработки: создание пакета программных продуктов по математике для студентов, специалистов и руководителей предприятий и организаций сферы производства и услуг столичного мегаполиса.

В ходе реализации научно-образовательной разработки поставлены и решены следующие задачи:

- разработаны алгоритмы программных модулей:

• «Формирование плана выпуска продукции». В основе этого модуля лежит задача линейного программирования, которая решается методом Жордана - Гаусса. Идея метода состоит в том, что описательная задача переводится в математическую форму (формализация). Формализованная задача должна содержать целевую функцию и уравнение ограничений. Затем выполняется переход к канонической форме и матричной записи. Алгоритм метода состоит в том, что по определенному плану строятся вспомогательные матрицы, и каждый шаг приближает к желаемому результату.
  

Алгоритм:

1. определить ведущий элемент, столбец, строку
   
2. составить уравнения пересчетов элементов в матрице
   
3. выполнить пересчет элементов матрицы
   
4. проверить результат пересчета на оптимальность
   
5. если решение оптимально, то прекратить вычисления; если же нет, то перейти к п.1
   

Признаком оптимального решения, является наличие в векторе решения только отрицательных или нулевых коэффициентов. Результат записывается по нулевым коэффициентам вектора решения.

Ведущим столбцом может быть назван любой столбец t матрицы, который удовлетворяет одному из условий:

1. первый столбец содержит положительный элемент в векторе решений
   
2. столбец содержит наибольший положительный элемент в векторе решений
   
3. если столбец t удовлетворяет условию:
   

c_i⁰a_k⁰ b_i⁰

_____ = max { c_j⁰ min ___ } – для max

a^ok a_ij⁰

причем C_j⁰ - коэффициент целевой функции в столбце i

a_ij - элемент матрицы а на пересечении i- строки и j-столбца

c_i⁰a_k⁰ b_i⁰

_____ = min { c_j⁰ max ___ } – для min

a^ok a_ij⁰

Вариант 2 выбора ведущего столбца является наилучшим, т.к. редко уменьшает количество пересчетов в матрице. Вычисление по варианту 3 выполняются только для элементов столбца, больших 0.

Примечание:

Вариант 3 является наилучшим для определения ведущего элемента, т.к. резко уменьшается количество пересчетов матрицы.

• «Оптимизация плана выпуска продукции». В основе этого модуля лежит задача целочисленного программирования, которая решена методом Гомори.
  

Метод Гомори решения задач целочисленного программирования является методом отсечения. Сущность его состоит в том, что сначала задача решается как задача линейного программирования без учета условия целочисленности переменных. Если полученное решение задачи линейного программирования является целочисленным, задача целочисленного программирования также решена и найденное решение является оптимальным и для неё. Если же в найденном решении задачи линейного программирования одна или большее число переменных не целые, то для отыскания целочисленного решения задачи добавляется новое ограничение. Это ограничение линейное, и при продолжении решения дополненной задачи симплексным методом с учетом этого ограничения получается целочисленный план.

Для нахождения целочисленного решения задачи методом Гомори используется следующий алгоритм:

1) Если в результате решения задачи линейного программирования в полученном оптимальном векторе X*(x1*,x2*,…,xn*) переменная xi*-нецелая, то следует найти её дробную часть и дробные части всех коэффициентов при переменных i-й строки. Под дробной частью числа a понимается наименьшее неотрицательное число такое, что разность между ним и a есть целое число;

2) Составить неравенство Гомори



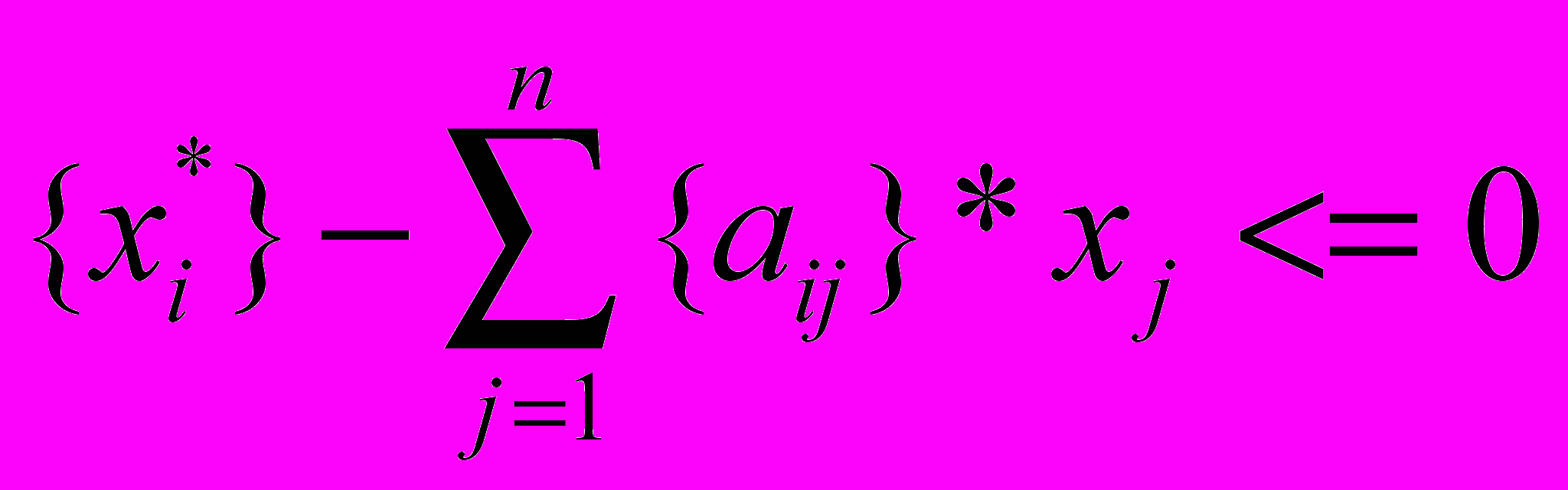
и включить его в систему ограничений исходной задачи.

3) Решить расширенную задачу.

Если нецелых переменных несколько, то для составления неравенства Гомори выбирается та, у которой целая часть наибольшая. Если решение расширенной задачи нецелое, то нужно повторять алгоритм метода Гомори вплоть до получения целочисленного решения. Оценки найденного целочисленного решения могут не удовлетворять критерию оптимальности симплексного метода.

• «Стратегия поведения в условиях конкуренции».
  

В практической деятельности весьма часто рассматривать явления и ситуации, в которых участвуют две или более стороны, имеющие различные интересы и обладающие возможностями применять для достижения своих целей разнообразные действия. Подобные явления и ситуации принято называть конфликтными или просто конфликтами. Конфликт может выражаться в виде конкурентной борьбы.

Заинтересованные стороны называются игроками. Любое возможное для игрока действие (в рамках заданных правил игры) называется его стратегиями. В условиях конфликта каждый игрок выбирает свою стратегию, в результате чего складывается набор стратегий, называемый ситуацией.

Одним из наиболее популярных классов игр являются матричные игры. Они находят широкое применение в экономике, с их помощью создаются оптимальные стратегий поведения на рынке.

Решение поставленной задачи начинается с поиска равновесной ситуации. По всем строками матрицы определяются минимумы, а среди этих минимумов выбирается максимум (максимин). Это выбранное число (a=maxmin) является одним из элементов матрицы. Оно называется нижней ценной игры. По всем столбцам матрицы определяются максимумы, а среди них выбирается минимум (минимакс). Это число (b=minmax) называется верхней ценой игры. В том случае, когда нижняя цена игры равна верхней цене игры, их общее значение называют просто ценой игры и обозначают v. Цена игры совпадает с элементом a(i, k) матрицы игры A, расположенным на пересечении i-й строки и k-го столбца, - минимальным в своей строке и максимальным в своем столбце. Этот элемент называется седловой точкой матрицы A или точкой равновесия, а про игру, говорят, что она имеет седловую точку. Стратегии А(i) и B(k), соответствующие седловой точке, называют оптимальными, а совокупность оптимальных ситуаций и цены игры – решением матричной игры с седловой точкой. Седловых точек в матричной игре может быть несколько, но все имеют одно и то же значение.

В случае же когда нижняя цена игры a и верхняя цена игры b не совпадают, ищутся оптимальные смешанные стратегии. Далее применяется правило доминирования. Оно заключается в том, что в ряде случаев анализ платежной матрицы обнаруживает, что некоторые чистые стратегии не могут внести никакого вклада в искомые оптимальные смешанные стратегии. «Отбрасывание» подобных стратегий (отбрасывание дублирующихся строк и столбов, а так же доминирующих) позволяет заменить первоначальную матрицу на матрицу выигрышей меньших размеров. Дублирующими называются полностью одинаковые строки и столбцы. Доминирующей строкой называется строка, все ячейки которой больше или равны соответствующим элементам другой строки. Доминирующие столбцы – столбцы, все элементы которого меньше или равны соответствующим элементам другого столбца.

При отбрасывании доминируемых строк и столбцов некоторые из оптимальных стратегий могут быть потеряны. Однако цена игры не изменится, и по усеченной матрице может быть найдена хотя бы одна пара оптимальных смешанных стратегий.

Таким образом, матрица сводится и размеру 2*2 или 2*n. Затем строятся две прямые и точка их пересечения. Это и будет решением данной задачи.

- выполнено написание программных кодов указанных программных модулей и их отладка;

- проведена пробная эксплуатация трех программных модулей, входящих в пакет прикладных программных продуктов;

- разработаны документы для внедрения пакета прикладных программных продуктов в практику образовательной программы для студентов, специалистов и менеджеров по управлению технологическими процессами.

Область применения:

Подготовленный пакет прикладных программных продуктов по направлению «Разработка и апробация серии электронных образовательных ресурсов по математике» является научным обоснованием концепции профессионально-образовательной программы в области совершенствования профессиональной компетентности менеджеров по управлению технологическими процессами и управления качеством предоставления образовательных услуг и может быть применим:

1) как основа интегрирования результатов научного поиска в сфере формирования планов производства и стратегий поведения на рынке в условиях конкуренции для предприятий малого и среднего бизнеса столичного мегаполиса;

2) в качестве единого пакета прикладных программных продуктов, а также отдельных самостоятельных программных модулей, в целях проведения обучения в системе повышения квалификации и профессиональной переподготовки руководителей и специалистов предприятий и организаций сферы производства и услуг по проблемам эффективного управления предприятиями малого и среднего бизнеса в сфере производства и оказания услуг населению;

3) как методика и практическое пособие для внедрения в практику и реализации в процессе жизнедеятельности предприятий и организаций сферы производства и услуг.

Образовательная программа.

Научно-образовательные материалы по направлению «Разработка и апробация серии электронных образовательных ресурсов по математике» разработаны на основе требований государственного образовательного стандарта высшего профессионального образования по специальности 230400.62 Информационные системы и технологии.

Серия электронных образовательных ресурсов по математике включает в себя три модуля, отражающих различные теоретико-методические и содержательно-технологические аспекты многогранной, полифункциональной и комплексной профессиональной подготовки студентов:

- модуль «Формирование плана выпуска продукции»,

- модуль «Оптимизация плана выпуска продукции»,

- модуль «Стратегия поведения в условиях конкуренции».

Основными целями и задачами изучения дисциплин модуля «Формирование плана выпуска продукции» являются:

- ознакомление с актуальными методами планирования выпуска изделий,

- изучение процедуры выполнения расчетов по определению плана выпуска изделий,

- формирование у слушателей фундаментальных и профессионально-прикладных знаний в области разработки математических моделей производственных процессов;

- формирование умений аналитического анализа созданных моделей;

- формирование у слушателей практических навыков работы с математическими моделями.

Основными целями и задачами изучения дисциплин модуля «Оптимизация плана выпуска продукции» являются:

- ознакомление слушателей с актуальными методами построения математических моделей, с целью оптимизации плана выпуска продукции;

- формирование у слушателей профессиональных компетенций в области управления производством малого и среднего бизнеса;

- формирование у слушателей практических навыков работы с математическими моделями.

Основными целями и задачами изучения дисциплин модуля «Стратегия поведения в условиях конкуренции» являются:

- формирование у слушателей системных представлений о стратегиях поведения на рынке в условиях конкуренции;

- освоение слушателями системных теоретико-методических знаний о критериях риска;

- формирование и развитие у слушателей умений составления математических моделей в условиях неопределенности;

- формирование у слушателей навыков анализа созданных моделей и принятия управленческого решения.

Таким образом, программа серии электронных образовательных ресурсов по математике включает в себя дисциплины:

- направленные на формирование у слушателей способностей принятия и практического осуществления результативных решений в области управления предприятием малого или среднего бизнеса,

- направленные на формирование у слушателей практических навыков, ориентированных на внедрение инноваций в сфере управления предприятием или организацией по производству товаров или оказания услуг населению столичного мегаполиса.

В целом же по результатам реализации федеральным государственным бюджетным образовательным учреждением высшего профессионального образования «Российский государственный социальный университет» проекта «Разработка и апробация серии электронных образовательных ресурсов по математике» можно констатировать, что: обучение слушателей осуществлялось с применением современных образовательных технологий и средств обучения; дисциплины учебного плана осваивались слушателями на основе современных учебно-образовательных методик и технологий.

Отчетная продукция: В качестве отчетной продукции по данном этапу реализации проекта представлены научно-образовательные материалы «Разработка и апробация серии электронных образовательных ресурсов по математике». Отчетные материалы в соответствии с Техническим заданием представлены на электронном носителе (CD) в формате Microsoft Word.