Iii. Численные методы алгебры. Лекция 9
| Вид материала | Лекция |
СодержаниеТ- оператор, определенный на замкнутом множестве S 3.2. Метод простых итераций для функциональных уравнений. S, взяв в качестве начала приближения точку . 3.3.Метод Ньютона. |
- Рабочей программы учебной дисциплины в. 8 Численные методы Уровень основной образовательной, 55.63kb.
- Рабочей программы учебной дисциплины в. 3 Численные методы Уровень основной образовательной, 51.78kb.
- Учебной дисциплины «Численные методы» для направления 010200. 62 «Математика и компьютерные, 59.05kb.
- Учебной дисциплины «Численные методы» для направления 010400. 62 «Прикладная математика, 58.48kb.
- Рабочая программа по разделу «Численные методы в строительстве», 71.92kb.
- Некоммутативная геометрия, 36.84kb.
- Рабочая программа учебной дисциплины численные методы Направление подготовки 210400, 273.35kb.
- Рабочая программа спец курса «Численные методы и математическое моделирование» Специальность, 53.73kb.
- Рабочая учебная программа дисциплины Численные методы и прикладное программирование, 299.02kb.
- Программа школы-конференции «алгебры ли, алгебраические группы и теория, 53.74kb.
Глава III.
Численные методы алгебры.
Лекция 9.
3.1. Принцип сжатых отображений.
Пусть Х – полное метрическое пространство,
 - расстояние между элементами х и у. Пусть, кроме того, S – замкнутое ограниченное множество (компакт): S
- расстояние между элементами х и у. Пусть, кроме того, S – замкнутое ограниченное множество (компакт): S X и Т – оператор (вообще говоря, – нелинейный), действующий из S в S, то есть отображающий множество S в себя:
X и Т – оператор (вообще говоря, – нелинейный), действующий из S в S, то есть отображающий множество S в себя: .
.Назовем точку

 неподвижной точкой оператора Т, если
неподвижной точкой оператора Т, если х*=Тх* (1)
Таким образом, неподвижные точки оператора Т являются решениями уравнения (1). Наиболее простой способ решения этого уравнения – итерационный, начиная с некоторого значения х0
хn+1=Txn , х0
 (2)
(2)При этом важно, чтобы такая последовательность {xn} сходилась к единственной точке х*. Следующая теорема формулирует достаточные условия сходимости итерационного процесса (2).
Теорема 1. (Принцип сжатых отображений).
Пусть Т – оператор сжатия на S, то есть
 и
и  (3)
(3)Тогда в S существует единственная неподвижная точка оператора Т, являющаяся пределом последовательности {xn} , определяемой процедурой итераций, начиная с
 . При этом скорость сходимости оценивается неравенствами:
. При этом скорость сходимости оценивается неравенствами:  (4)
(4)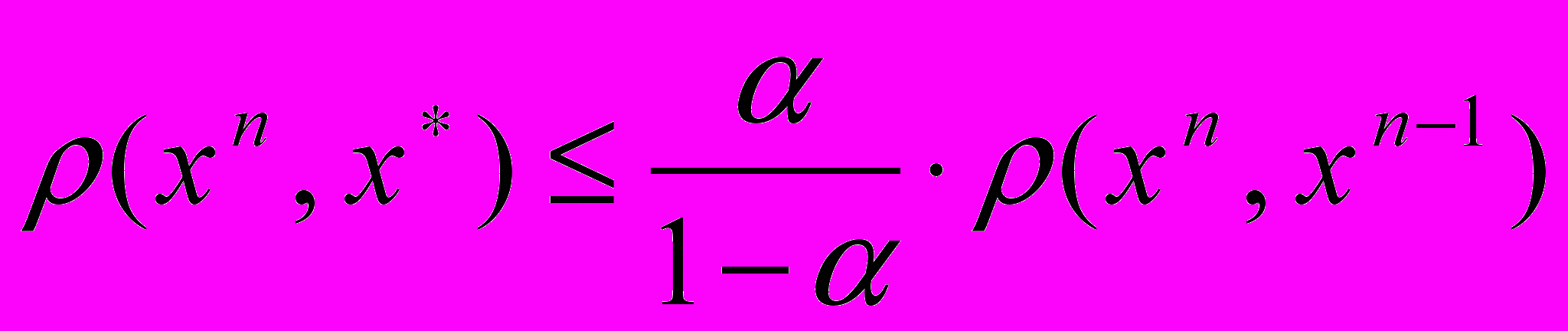 (5)
(5) Докажем, что последовательность {xn} – фундаментальная. Рассмотрим
Докажем, что последовательность {xn} – фундаментальная. Рассмотрим  (6)
(6)Далее при p>1 имеем
 {неравенство треугольника: вставим точку
{неравенство треугольника: вставим точку 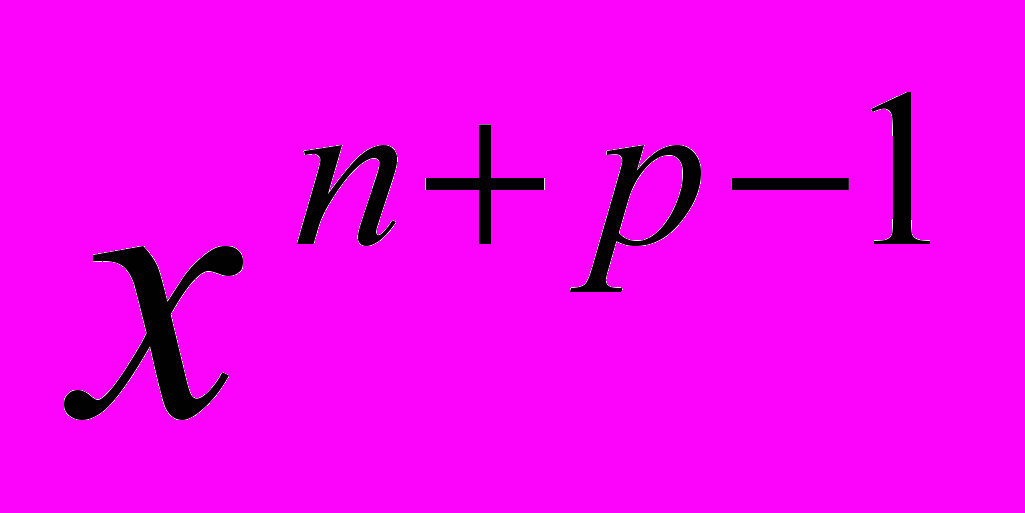 }
}
 {продолжая вставлять точки}
{продолжая вставлять точки}
 {на основании (6)}
{на основании (6)}
 {геометр. прогрессия}
{геометр. прогрессия}

 . (7)
. (7)Отсюда следует, что
 ,
, 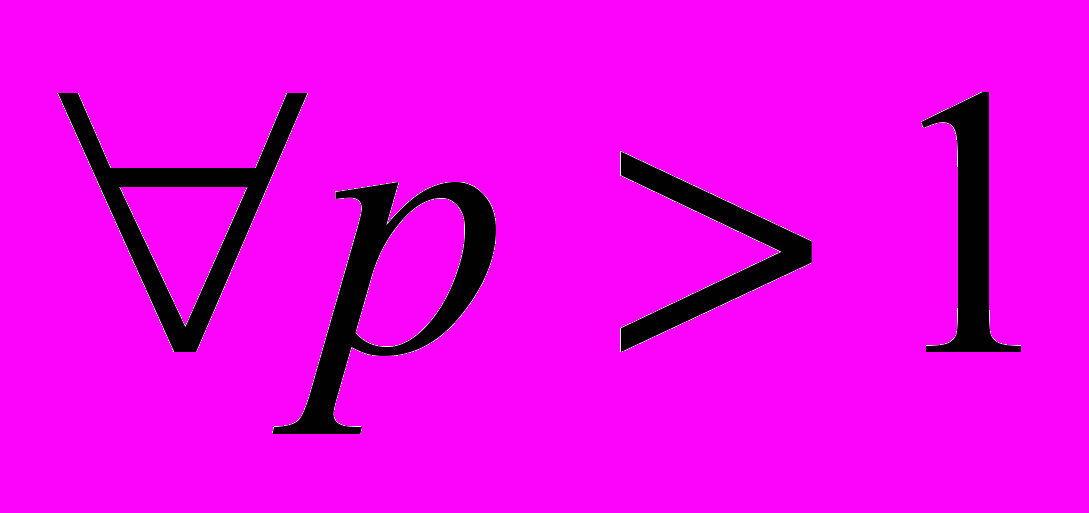
следовательно, последовательность {xn} – фундаментальная, и согласно критерию Коши-Вейерштрасса последовательность {xn} сходится к элементу
 (так как S - компакт). Таким образом, имеем
(так как S - компакт). Таким образом, имеем .
.Далее
 .
.Следовательно,
 .
.Докажем единственность неподвижной точки х*.
От противного. Пусть
 : х*=Тх*, у*=Ту*. Тогда
: х*=Тх*, у*=Ту*. Тогда  .
.Но это противоречие.
Формула (4) следует из формулы (7) при р
 :
:  ,
,т.к. правая часть неравенства (7) не зависит от р.
Докажем (5):
 {неравенство треугольника}
{неравенство треугольника}


 .
.Отсюда
 .
.Если разделить обе части этого неравенства на (1-α), то получим (5).

Замечание 1.
Неравенство (4) показывает, что последовательность {xn} сходится к х* со скоростью геометрической прогрессии (такая скорость называется линейной: каждый шаг в
 раз приближает к х*). Кроме того, неравенство (4) позволяет определить, сколько итераций (шагов) необходимо сделать для достижения заданной точности
раз приближает к х*). Кроме того, неравенство (4) позволяет определить, сколько итераций (шагов) необходимо сделать для достижения заданной точности 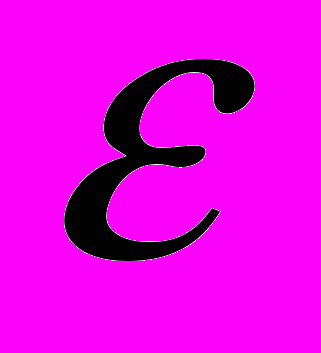 . Для этого нужно решить неравенство:
. Для этого нужно решить неравенство: 
Ясно, что для хорошей оценки числа итераций необходимо точнее оценивать константу сжатия
 , что на практике не всегда просто сделать. При реализации алгоритма полезно также использовать неравенство (5), позволяющее контролировать каждый шаг итерации и установить следующий критерий останова:
, что на практике не всегда просто сделать. При реализации алгоритма полезно также использовать неравенство (5), позволяющее контролировать каждый шаг итерации и установить следующий критерий останова: .
.Теорема 2.
Пусть Х – банахово пространство, то есть полное нормированное пространство с нормой элементов
 . Т- оператор, определенный на замкнутом множестве S и отображающий S в себя. Тогда, если выполняется условие
. Т- оператор, определенный на замкнутом множестве S и отображающий S в себя. Тогда, если выполняется условие  (8)
(8)(это условие Липшица с константой
 ), то справедливо утверждение теоремы 1.
), то справедливо утверждение теоремы 1. Действительно, положим
Действительно, положим  результат.
результат. 
3.2. Метод простых итераций для функциональных уравнений.
Утверждение 1.
Пусть
 (одномерный случай) и задана функция f(x), удовлетворяющая условию:
(одномерный случай) и задана функция f(x), удовлетворяющая условию: (9)
(9)(Условие Липшица с константой
 на отрезке [a,b].)
на отрезке [a,b].)Тогда оператор f(x) - сжимающий и уравнение f(x)=х имеет единственную неподвижную точку, которую можно найти методом простых итераций:
 .
. Действительно, определим
Действительно, определим  . Следовательно, выполняется условие (8) теоремы 2, откуда и следует результат.
. Следовательно, выполняется условие (8) теоремы 2, откуда и следует результат. 
Утверждение 2.
Пусть
 , причем
, причем  (10)
(10)Тогда оператор f(x) является сжимающим.
 Согласно теореме о среднем
Согласно теореме о среднем .
.Оценим это неравенство по модулю:
 .
.Это говорит о том, что выполняется условие (9) утверждения 1, значит, f(x) действительно сжимающий оператор.

Рассмотрим задачу поиска корней уравнения
 . Пусть известны границы для корня этого уравнения и мы хотим найти этот корень методом итераций. Если удастся привести уравнение к виду x=f(x), так чтобы выполнялось одно из условий утверждения 1 или утверждения 2, то в этом случае можно будет применить метод итераций. Такое преобразование, вообще говоря, не единственно, причем главная трудность заключается в определении того замкнутого ограниченного множества S (а в одномерном случае – отрезка [a,b]), для которого помимо условия сжатости, выполняется условие
. Пусть известны границы для корня этого уравнения и мы хотим найти этот корень методом итераций. Если удастся привести уравнение к виду x=f(x), так чтобы выполнялось одно из условий утверждения 1 или утверждения 2, то в этом случае можно будет применить метод итераций. Такое преобразование, вообще говоря, не единственно, причем главная трудность заключается в определении того замкнутого ограниченного множества S (а в одномерном случае – отрезка [a,b]), для которого помимо условия сжатости, выполняется условие  .
.Утверждение 3.
Определим множество
 - замкнутый r-“шар” с центром в точке х0 (в одномерном случае – отрезок). Пусть оператор Т - сжимающий на S и выполняется следующее условие:
- замкнутый r-“шар” с центром в точке х0 (в одномерном случае – отрезок). Пусть оператор Т - сжимающий на S и выполняется следующее условие: (11)
(11)Тогда для любой точки
 выполняется:
выполняется:  .
. Достаточно доказать, что
Достаточно доказать, что 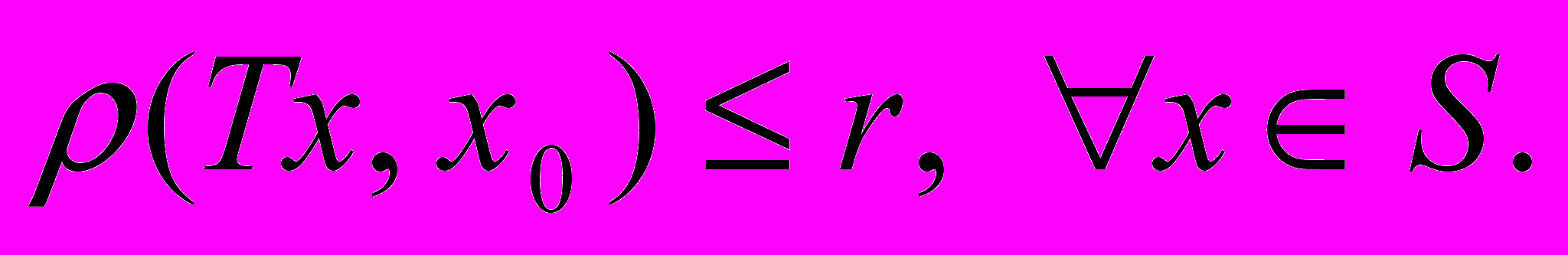 Имеем:
Имеем: {неравенство треугольника}
{неравенство треугольника}
 .
. 
Пример 1.
Решить уравнение
 .
. Приведем к виду:
Приведем к виду: (12)
(12)Г
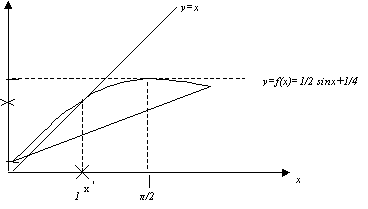
рафическая иллюстрация.

Найдем первую производную:
 .
.При
 и
и  =0,5
=0,5 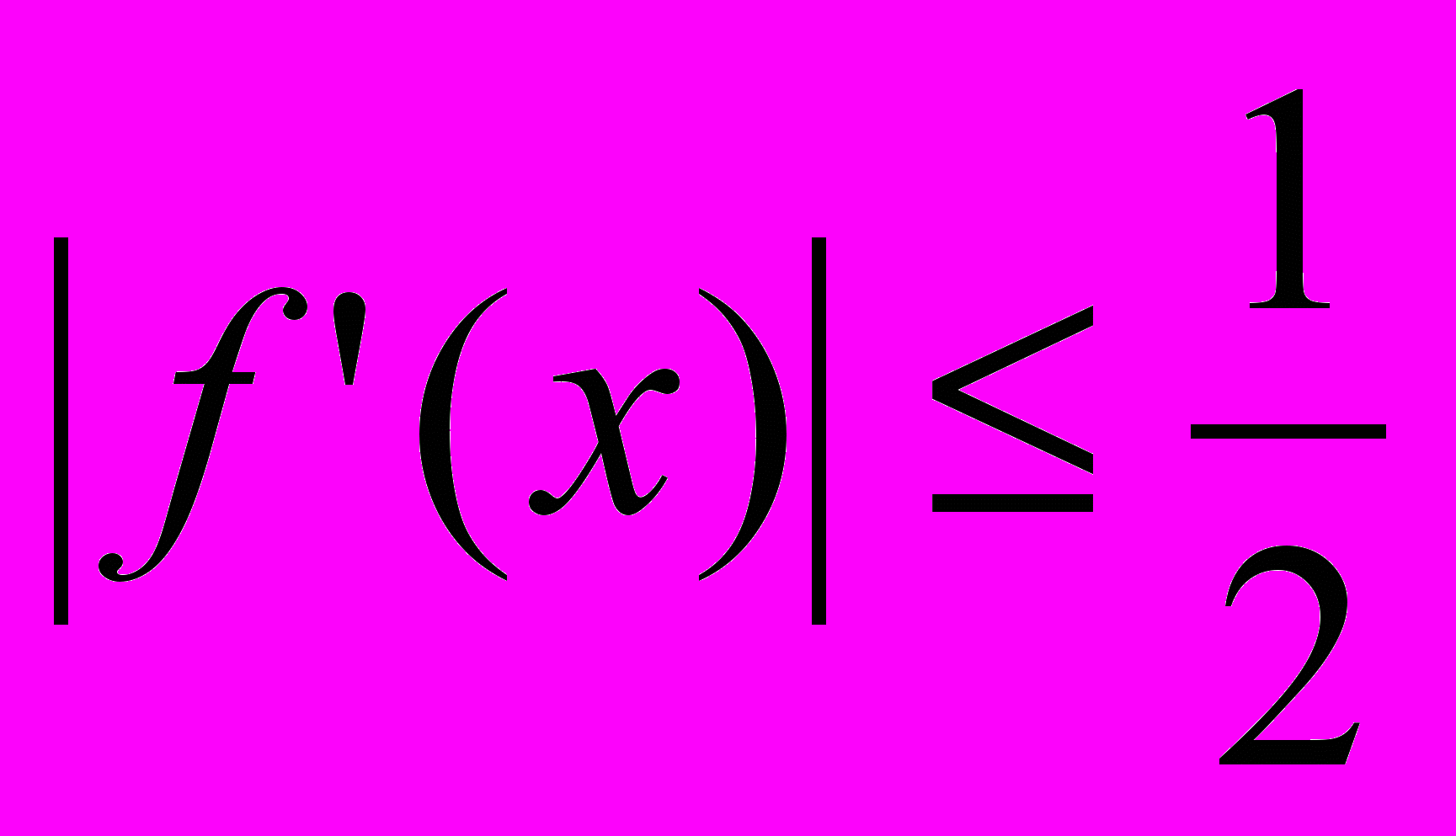 (значение
(значение 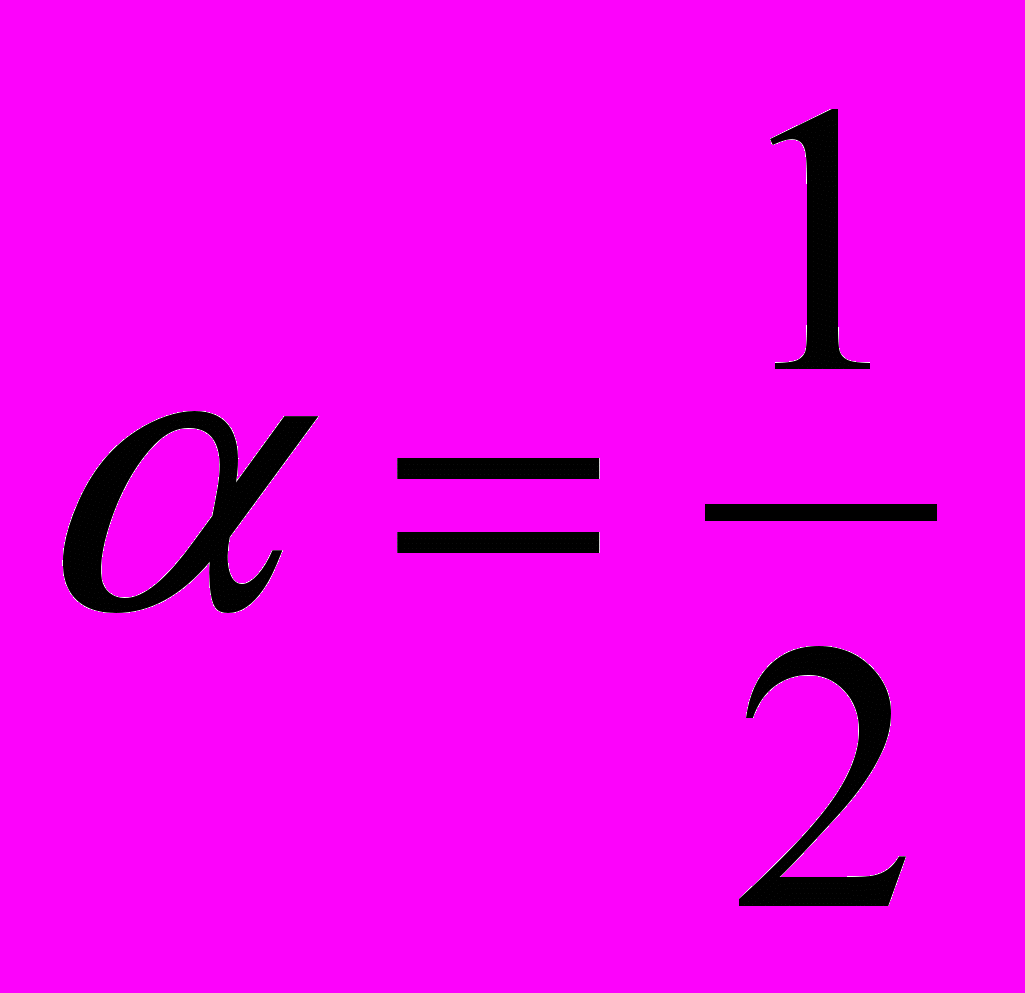 можно использовать в итерациях).
можно использовать в итерациях).Можно улучшить оценку для
 , если заметить, что из (12) следует, что
, если заметить, что из (12) следует, что .
.Для простоты положим
 =0,5 и оценим радиус “шара” S, взяв в качестве начала приближения точку
=0,5 и оценим радиус “шара” S, взяв в качестве начала приближения точку 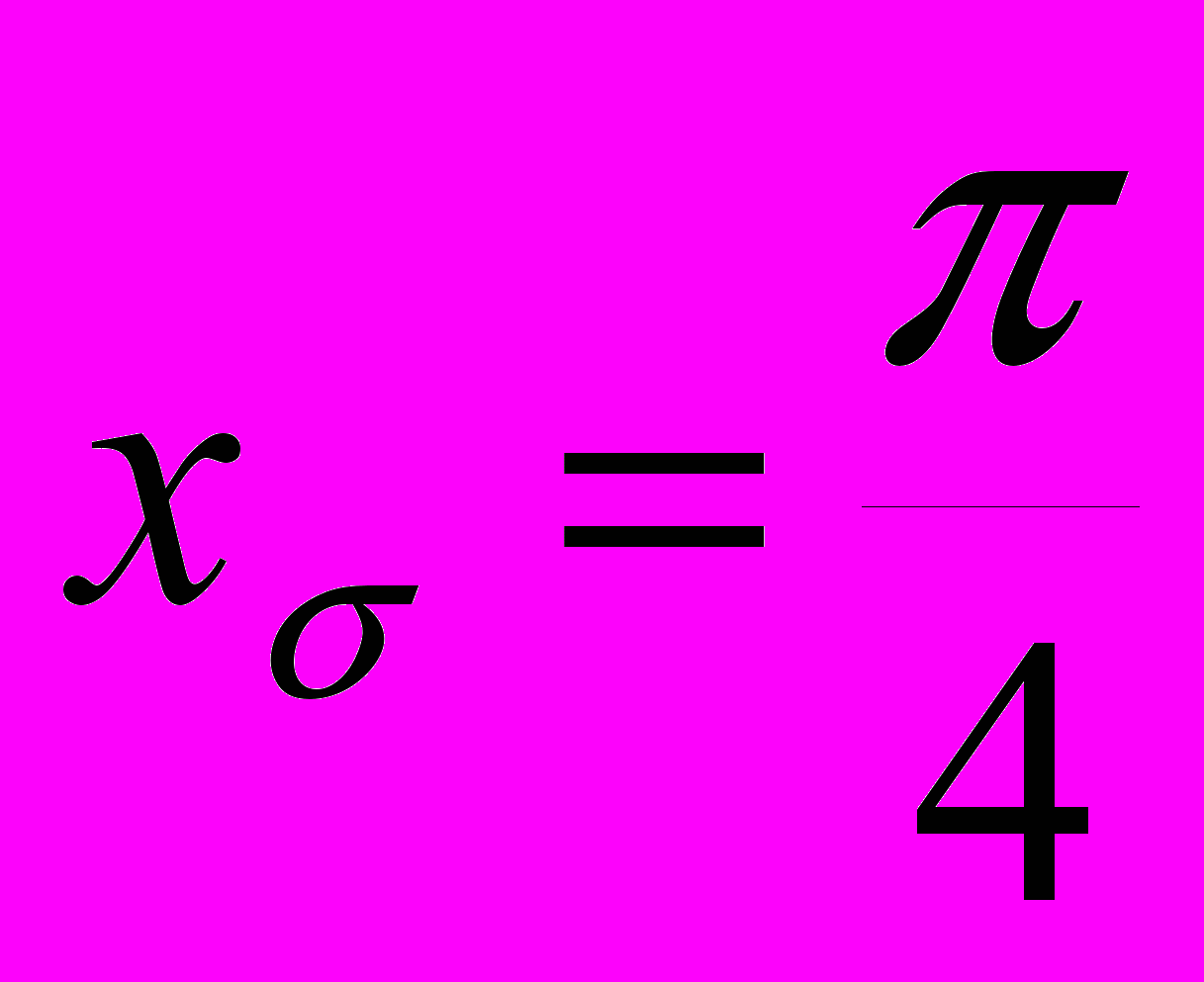 . Тогда получим:
. Тогда получим: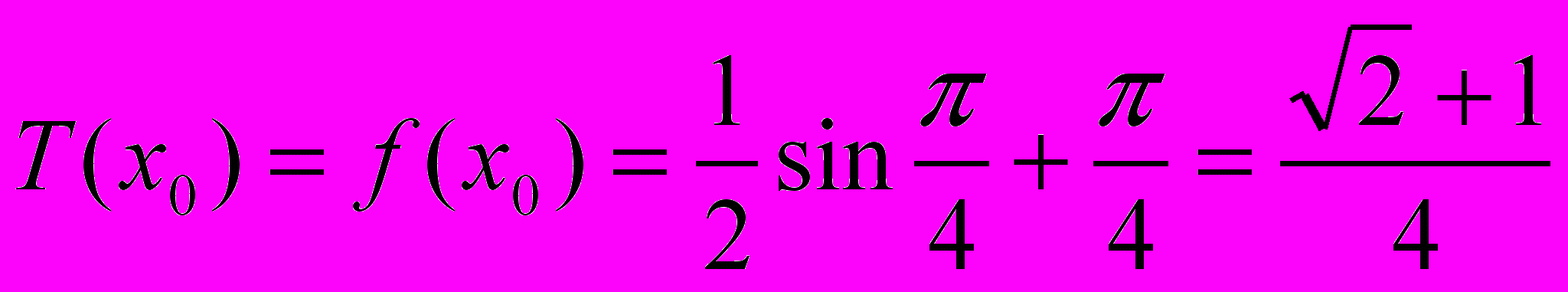 ;
;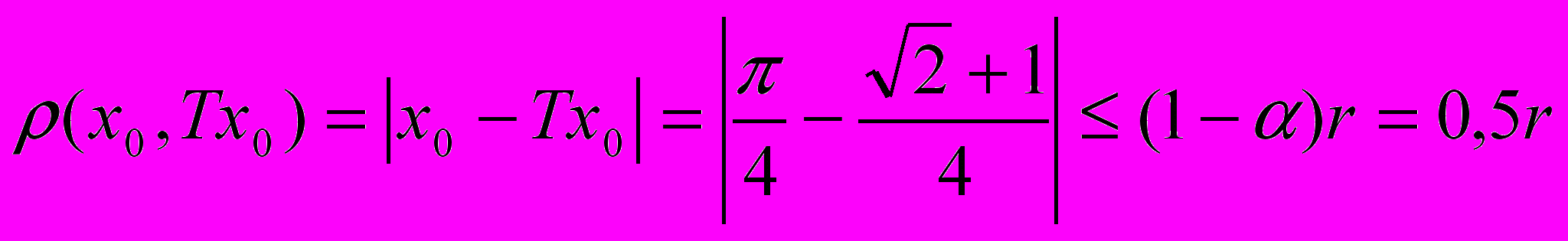 .
.То есть если положить
 , то
, тоусловие (11) выполняется. Последовательно найдем:
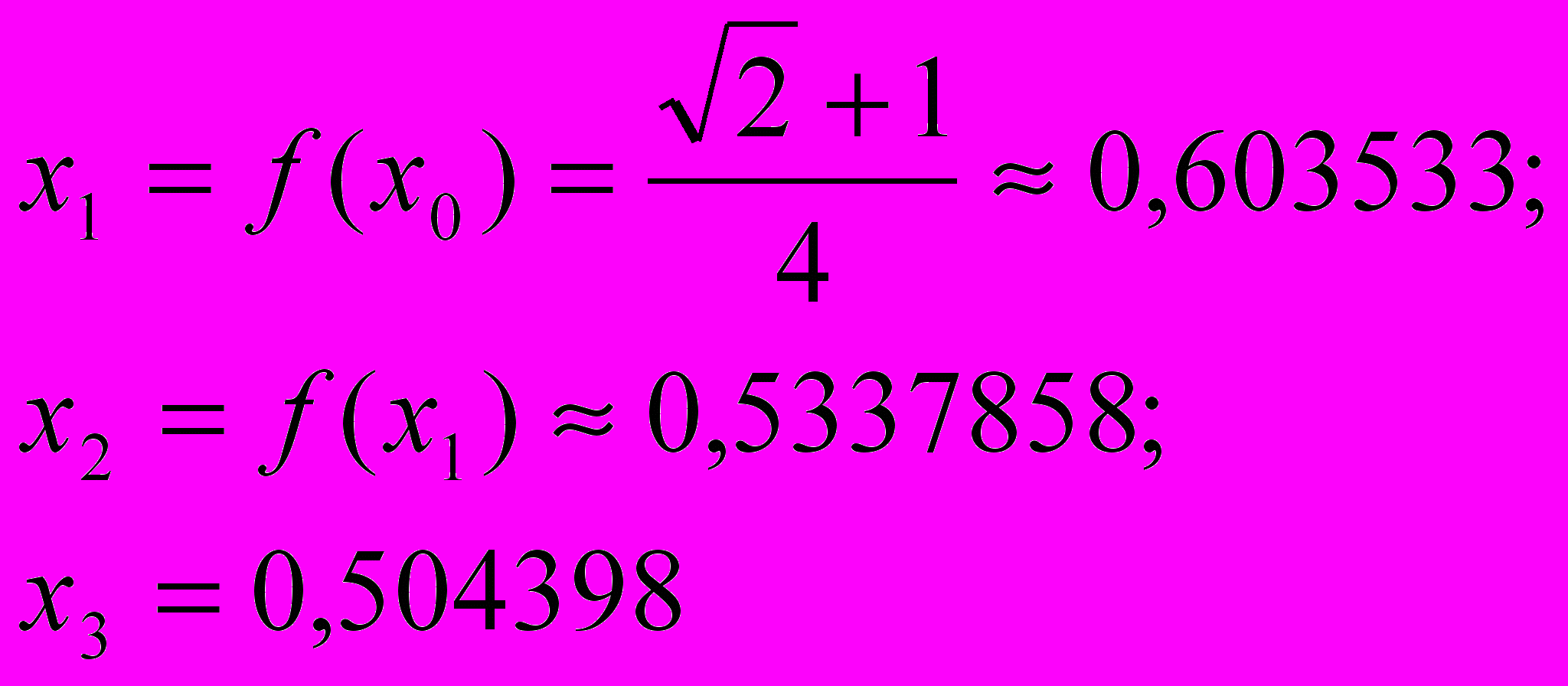
Продолжаем процедуру пока m значащих цифр после запятой не установятся, если задана точность
 . В данном случае, например, при
. В данном случае, например, при  придется сделать 8 итераций. Тогда х*=х8=0,4816 .
придется сделать 8 итераций. Тогда х*=х8=0,4816 . 
Пример 2.
F(x)=tgx-x , x[
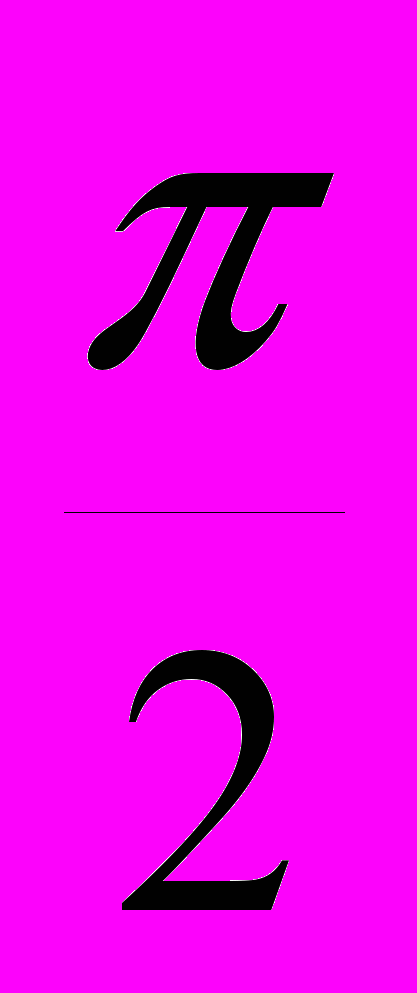 ;
;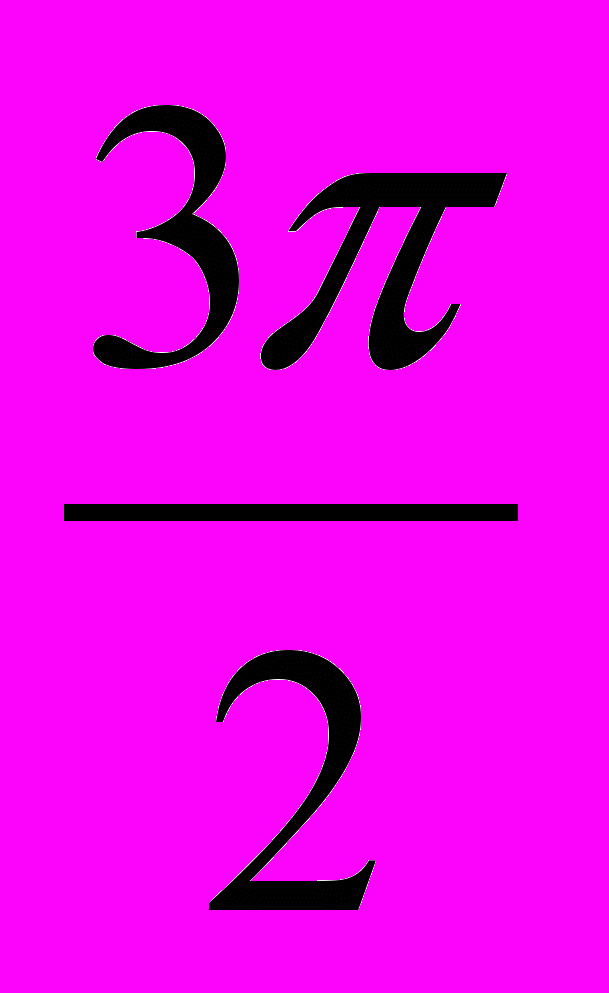 ].
]. Решить самостоятельно: построить график, затем сделав замену переменных:
Решить самостоятельно: построить график, затем сделав замену переменных:x =
 + arctg y, и привести уравнение к виду: y =
+ arctg y, и привести уравнение к виду: y =  + arctg y = f(y) - удовлетворяет принципу сжатых отображений. Оценить α и запустить процедуру для ε = 0,001.
+ arctg y = f(y) - удовлетворяет принципу сжатых отображений. Оценить α и запустить процедуру для ε = 0,001. 
3.3.Метод Ньютона.
Пусть снова задано уравнение
f(x)=0.
Запишем его в виде
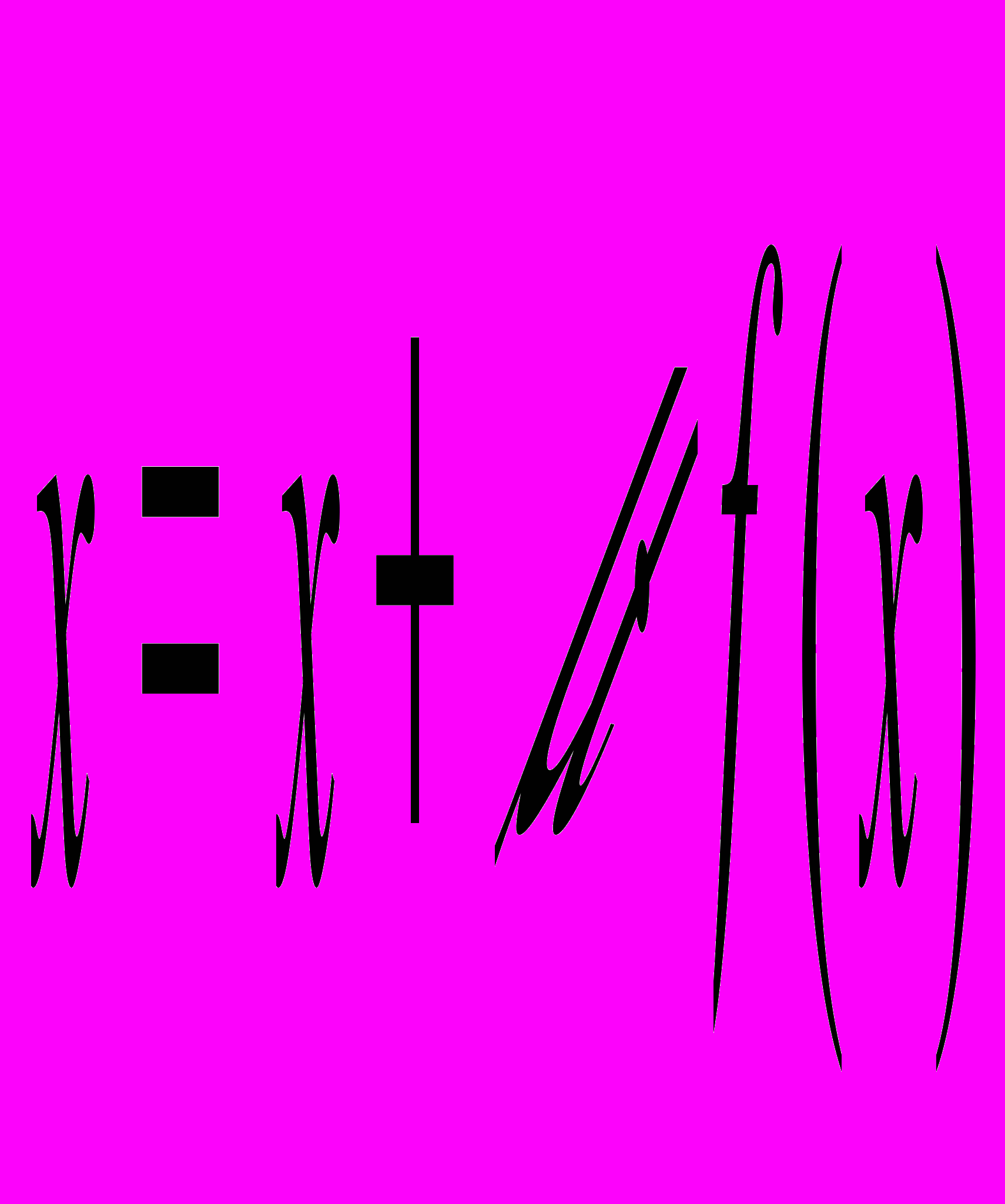 , где
, где 
и
 .
.Пусть хк – некоторое приближение к корню х*. Для ускорения сходимости итераций желательно, чтобы
 был как можно меньше. Положим
был как можно меньше. Положим  , то есть
, то есть 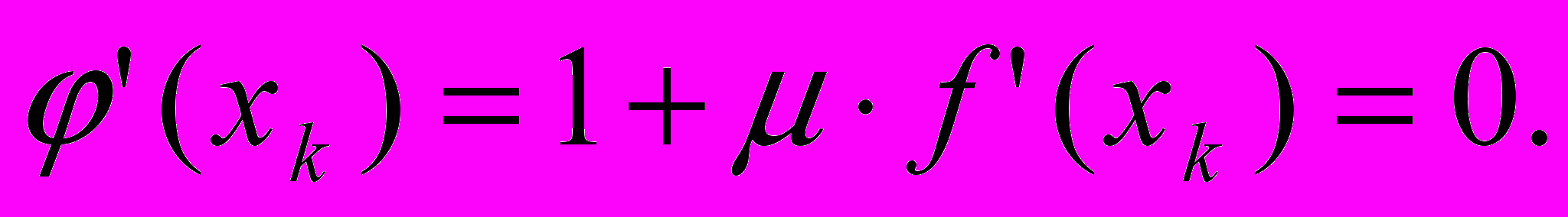
Отсюда находим, что
 .
.Подставляя в исходное уравнение, получаем рекуррентную формулу:
 .
.Это и есть итерационная процедура Ньютона.
