На уроках математики
| Вид материала | Урок |
- Рабочая программа по курсу Формирование исследовательских умений на уроках математики, 51.16kb.
- Методика использования дидактических игр на уроках математики в начальной школе Содержание, 677.9kb.
- Аннотированный список ресурсов Интернет «Нравственное воспитание на уроках математики», 18.81kb.
- Уроках математики посредством сообщения им сведений из истории науки, 158.2kb.
- Доклад на тему «Активизация мыслительной деятельности учащихся на уроках математики», 45.79kb.
- Активізація навчально-пізнавальної діяльності учнів на уроках математики, 19.25kb.
- Тематика курсовых работ по специальной методике преподавания математики Тема Особенности, 128.48kb.
- Епифанова Н. М. Ягпу проведение лабораторных и практических работ на уроках математики, 214.12kb.
- Использование средств наглядности на уроках математики примерное содержание, 8.18kb.
- Уроках математики, 33.41kb.
Комитет образования и науки города Новокузнецка
Отдел образования Центрального и Куйбышевского районов
МОУ «Лицей № 47»
ИМИТАЦИОННЫЕ, ДЕЛОВЫЕ ИГРЫ
НА УРОКАХ МАТЕМАТИКИ
г. Новокузнецк
2007год
Как известно, играют не только дети, играют и взрослые.
Существуют так называемые деловые игры, в процессе которых на основе игрового замысла моделируется реальная обстановка, в которой выполняются конкретные действия, выбирается оптимальный вариант решения задачи и имитируется его реализация в практической жизни.
Более общим, является определение деловой игры как модели взаимодействия людей в процессе достижения некоторых целей — экономических, производственных, политических.
В любом случае деловая игра — это модель процесса принятия решений в реальной ситуации с четко выраженной структурой.
Деловая игра позволяет создавать производственные ситуации, в ходе которых играющему необходимо найти правильную линию поведения, оптимальное решение проблемы, соответственно реальным обстоятельствам производства, имитированным в игре.
В ходе игры каждому участнику необходимо максимально мобилизовать все свои знания, опыт, воображение. Особенно ценно то, что здесь дело не сводится лишь к механическому использованию программного материала. В процессе игры вырабатывается умение мыслить системно, продуктивно, пробуждается стремление к поиску новых идей, а это уже шаг к творчеству.
Деловые игры получают в последнее время все большее распространение при обучении студентов. Однако они могут и должны применяться при обучении школьников. Ведь учащиеся VI—XI классов в условиях игры охотно перевоплощаются в тех или иных специалистов и выступают в адекватной роли в моделируемой обстановке.
Приведем примеры использования деловой игры на уроках математики.
Деловая игра «Строитель»
Тема: «Площади многоугольников» (IX класс).
Цель урока: усвоение учащимися формул для вычисления площадей параллелограмма, треугольника, трапеции и применение полученных знаний к решению практических задач.
Воспитательная цель: ориентация учащихся на профессию строителя.
В начале урока учитель знакомит учащихся IX класса со строительным производством и одной из наиболее распространенных строительных профессий — столяра.
I этап:
Строительное производство сегодня — это механизированный процесс сборки зданий и сооружений из крупноразмерных деталей, изготовленных заводским способом. Столяр работает в строительно-монтажных организациях, на деревообрабатывающих предприятиях, в столярных мастерских. Он выполняет различные операции на станках: на круглопильных — раскрой пиломатериалов, на фуговальных — строгание, на долбежных и шипорезных — выдалбливание гнезд и зарезание шипов у заготовок.
Непосредственно на строительном объекте столяр устанавливает оконные и дверные блоки, производит настилку дощатых и паркетных полов, монтирует встроенную мебель и т. д. Выполнение такой работы невозможно без знания устройства и правил эксплуатации деревообрабатывающих станков,
знания технологии и организации строительного производства, умения читать чертежи. Профессия требует объемного воображения, хорошего глазомера, знания геометрии, рисования, черчения.
Постановка задачи.
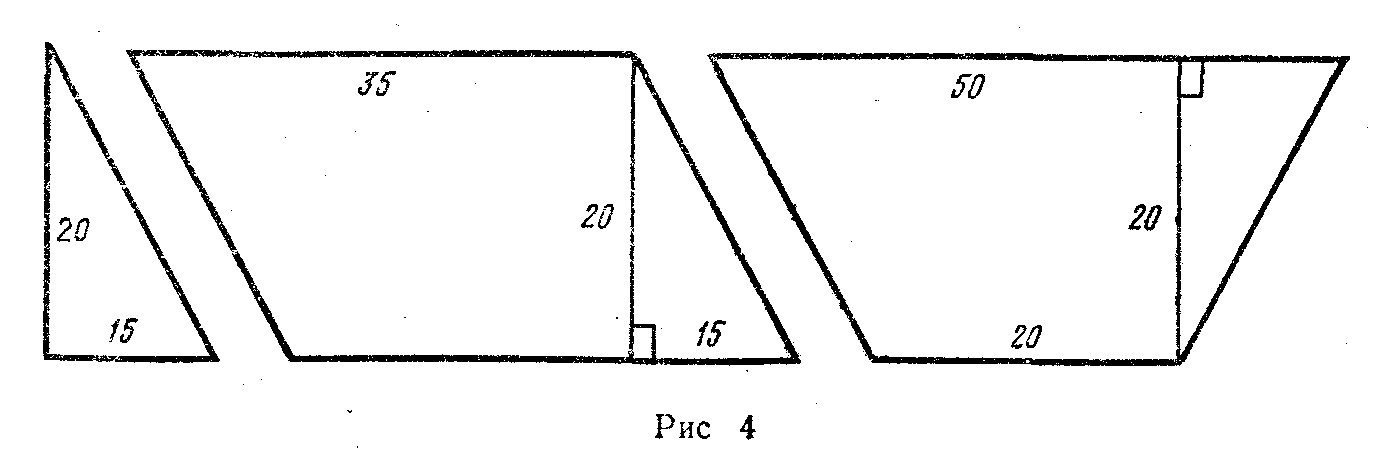
Учитель объявляет, что сегодня все ученики будут выступать в роли строителей. Требуется выполнить работу по настилке полов строящегося детского сада. Предлагается произвести настилку паркетного пола в игровом зале размером 5,75Х8 м. Паркетные плитки имеют форму прямоугольных треугольников, параллелограммов и равнобочных трапеций. Размеры плиток в сантиметрах указаны на рисунке 4.
Правила игры:
Учащиеся разбиваются на три бригады. Избираются бригадиры.
Первая бригада—столяры.
Им нужно изготовить паркетные плитки указанных размеров в таком количестве, чтобы после настилки пола не осталось лишних плиток и число треугольных плиток было минимальным, а плиток в форме параллелограммов и трапеций — одинаковое количество.
Вторая бригада — поставщики.
Им нужно доставить необходимое количество плиток на строительную площадку. Они рассчитывают это количество.
Третья бригада — паркетчики.
Чтобы проконтролировать доставку, надо наперед знать, сколько и каких паркетных плиток понадобится для покрытия пола.
Побеждает в игре та команда, которая первой выполнит правильный расчет. Для этого надо знать формулы для вычисления площадей вышеуказанных фигур.
Учитель записывает на доске, какой материал следует изучить.
Учащиеся приступают к работе с учебником.
Внутри каждой команды разрешаются взаимоконсультации. При необходимости консультацию дает учитель.
После того как теоретический материал изучен, а формулы для вычисления площадей параллелограмма, треугольника и трапеции записаны в тетрадях, учитель проецирует на доску рисунки и формулы по проработанному материалу.
Проводится проверка готовности бригад. С этой целью каждой команде предлагается по два-три вопроса.
Ответы учащихся оцениваются очками. Счет записывается на доске.
II этап:
Каждая команда приступает к практическим вычислениям.
Паркет укладывается в ряды так, что параллелограммы и трапеции чередуются, а треугольников в одном ряду всего два. Подсчеты показывают, что в одном ряду по ширине укладывается по два треугольника и по восемь параллелограммов и трапеций.
Действительно, площадь одной полосы шириной 20 см и длиной 575 см будет 11500 см2. Если площадь двух треугольников 300 см2, а площадь параллелограмма или трапеции 700 см2, то в одной полосе по ширине игрового зала поместится по 8 параллелограммов и трапеций: (11500 — 300): 700 == 16. Таких полос в длине комнаты поместится 800:20=40. Следовательно, для настилки пола понадобится 80 треугольников и по 320 параллелограммов и трапеций. Проверкой устанавливается: площадь игрового зала 575 X X 800 =460 000 см3, площадь одной полосы 575Х20=11500 см2, а таких полос 40, поэтому 11500 X 40 == 460 000 см2 — площадь паркетного пола.
Это самый ответственный этап игры. Вычисляются площади плоских фигур, производятся расчеты.
В конце второго этапа игры учащиеся из каждой бригады дают объяснения около стола учителя, как они вычислили нужное количество паркетных плиток.
Идет разговор об экономии материала. На первый план выступает математическое содержание работы. Происходит процесс применения знаний на практике.
На этом этапе игры команды получают определенное число очков, а правильно ответившие ученики — оценки в журнал.
На заключительном этапе учитель проверяет, насколько глубоко усвоили ученики материал. Для этого им предлагаются контрольные вопросы, которые могут быть, например, такими:
1. Дайте определение площади простых фигур.
2. Докажите, что площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
3. Докажите, что площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне.
4. Докажите, что площадь трапеции равна произведению полусуммы оснований на высоту.
5. По какому принципу укладывали паркетные плитки в один ряд?
6. Как проводились вычисления площади одного ряда плиток?
7. Дайте краткую характеристику профессии столяра.
В заключение подводятся результаты игры.
Рефлексия урока.
Заметим, что в менее подготовленных классах такую игру следует проводить с целью обобщения и применения знаний, после того как изучен материал о площадях плоских фигур.
Распределение времени при этом может быть таким:
- Рассказ учителя о профессии строителя — 5 мин.
- Постановка задачи с помощью ТСО — 3 мин.
- Работа с учебником (повторение формул площадей плоских фигур) — 8 - 10 мин.
- Вычисление количества плиток — 16—18 мин.
- Проверка глубины знаний учащихся — 8 мин.
- Сообщение домашнего задания — 3 мин.
Как видим, деловые игры представляют собой непрерывную последовательность учебных действий в процессе решения поставленной задачи. Этот процесс условно расчленяется на такие этапы: знакомство с профессией строителя; построение имитационной модели производственного объекта; постановка главной задачи бригадам и выяснение их роли в производстве; создание игровой проблемной ситуации; овладение необходимым теоретическим материалом; решение производственной задачи на основании математических знаний; проверка результатов; коррекция; реализация принятого решения; анализ итогов работы; оценка результатов работы.
Основная идея игры состоит в том, чтобы создать производственную ситуацию, в которой учащиеся, поставив себя на место человека той или иной специальности, смогут увидеть и оценить значение математических знаний в производительном труде, самостоятельно овладеть необходимым теоретическим материалом и применить полученные знания на практике.
Благодаря соревновательному характеру деловой игры активизируется воображение участников, что помогает им находить решения поставленной задачи.
Деловая игра «Проектировщик»
Тема: «Примеры решения задач с помощью движений» (IX класс).
В начале урока учитель сообщает, что сегодня каждый ученик должен представить себя в роли инженера-проектировщика. Будем строить дороги. Полезно знать, что 1 км дороги с асфальтовым покрытием обходится государству от 700 000 до 1 000 000 р.
Задание состоит в том, чтобы, используя свои знания по теме «Движения», выполнить вполне реальную инженерную задачу.
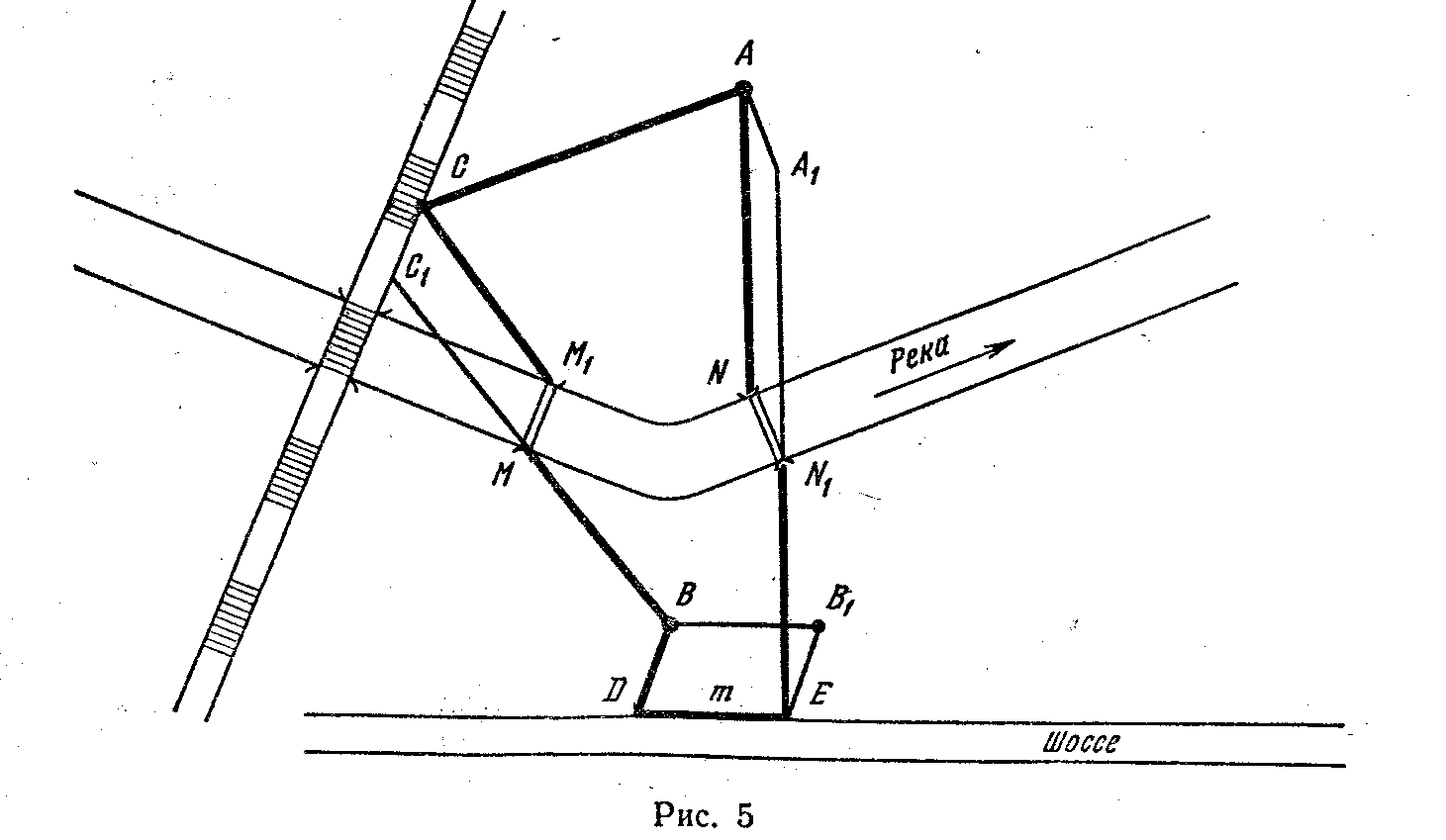
На доску проецируется рисунок 5 без проведенных участков дороги. Учитель объясняет задание.
На плане местности, в недрах которой найдены полезные ископаемые, необходимо спроектировать шоссейную дорогу, которая связала бы город А с железной дорогой (пункт С), дальше пункт С через реку с городом В. Город В находится вблизи уже существующей шоссейной дороги, вдоль которой надо спроектировать погрузочно-разгрузочную платформу DЕ длиной m и после этого конец платформы, пункт Е, соединить вновь через реку асфальтированной магистралью с городом A. По ходу дороги на реке надо спроектировать мосты. Строительство мостов производить только перпендикулярно берегам реки. Длина замкнутой дороги АСМ1МВDЕN1NА должна быть кратчайшей. У мостов М1М и N1N со временем будут построены порты М и N, первый со стороны города В, другой со стороны города А.
Класс делится на три проектных бюро (ПБ).
Во главе каждого из них ставится капитан команды. Он условно наделяется полномочиями начальника ПБ, а каждый ученик становится инженером-проектировщиком.
Каждой команде выдается план местности без ломаной АСМ1МВDЕN1NА в нескольких экземплярах и сообщается задание: первой команде спроектировать участок АСМ1МВ, второй — участок ВDЕ, третьей — участок ЕN1NА.
Учитель сообщает, что игра будет проходить в несколько этапов. В конце каждого этапа работники ПБ должны отвечать на контрольные вопросы, решать предложенные задачи, обосновывать принятые инженерные решения. В каждом ПБ разрешаются взаимопомощь и консультации.
Правильные ответы по теории, решению задач, проектированию дороги приносят очки команде и оценки в журнал учащимся. Нарушение дисциплины, невыполнение правил игры, подсказки приносят штрафные очки. Учитываются не только знания, но и организация работы ПБ, трудовая дисциплина коллектива, скорость и оптимальный вариант решения инженерной задачи.
На первом этапе игры происходит изучение каждой командой плана местности, на котором изображены города А и В, река, полотно железной и шоссейной дорог. Возникает необходимость перевести задание с инженерного языка на язык математики.
Для этого каждый ученик перерисовывает план в тетрадь, заменяя железную и шоссейную дороги прямыми линиями, а берега реки — параллельными прямыми. Железнодорожный мост построен перпендикулярно берегам реки.
Создается некоторая математическая модель — чертеж к задаче. За выполнение предварительных чертежей каждой команде проставляется число очков, равное числу учеников, правильно выполнивших чертеж. Решение данной инженерной задачи предъявляет к учащимся определенные требования в отношении знаний: чтобы работать в ПБ, надо знать математику. Необходимость в этих знаниях придает дидактической игре познавательный характер.
На втором этапе игры следует создать ориентировочную основу действий, используя имеющиеся знания. Для этого каждой команде предлагается одна из трех задач, решенных на предыдущих уроках. Условия и рисунки к задачам проецируются на доску.
Задача I команде. Две точки Р и Q размещены по одну сторону от прямой а. На данной прямой найти точку X, такую, чтобы сумма расстояний РХ+ХQ была наименьшей.
Задача II команде. По разные стороны реки с параллельными берегами а и b расположены два пункта К и L. В каком месте нужно построить мост, чтобы участок дороги, соединяющий пункты К и L, был кратчайшим?
Задача III команде. По одну сторону дороги размещены два пункта R и S. Где нужно построить у дороги платформу DЕ длиной т, чтобы участок дороги RDЕS был кратчайшим?
После того как в каждом ПБ учащиеся ознакомились с задачей, учитель предлагает, если это необходимо, повторить по учебнику: свойства осевой симметрии, параллельного переноса, равнобедренного треугольника и параллелограмма. По истечении отведенного времени подводится итог повторения. Счет записывается на доске. Во время повторения разрешаются консультации как внутри команд, так и со стороны учителя всему классу.
Третий этап работы — решение предложенных задач в каждом ПБ и переосмысливание его соответственно общему заданию. Через 8—10 мин каждый ученик должен уметь объяснить решение своей задачи. Поэтому внутри каждой команды идет напряженная работа — решить первыми и правильно.
Для ускорения изложений решений задач используются рисунки 6, 7, 8, спроецированные на доску. Для объяснения решения задачи из каждой команды вызываются 3—4 ученика, которые продолжают объяснение один за другим. Приводим примерное решение сформулированных задач.
Задача 1. Рассмотрим точку Q' —зеркальное отражение точки Q от прямой а (рис. 6). Тогда для любой точки F прямой а будем иметь FQ=FQ' и поэтому РF+FQ=РF+РQ'. Таким образом, сумма РF+FQ равна длине ломаной РFQ'. Следовательно, наименьшую длину сумма расстояний РF+FQ будет иметь в том случае, когда наименьшую длину будет иметь ломаная РFQ'. Но ломаная РFQ' будет иметь наименьшую длину, если она обратится в отрезок прямой, т. е. если роль точки F будет играть точка Х пересечения прямой а с отрезком PQ'. Эта точка Х и является искомой.
Задача 2. Представим себе, согласно рисунку 7, что берега реки слились. Это произошло вследствие параллельного переноса полуплоскости а, ограниченной прямой а, на ширину реки вдоль перпендикуляра к прямой b (рис. 7). Точка К переместилась вдоль направления моста на расстояние КК', равное его длине. Если считать, что река «исчезла», то задача стала проще. Мост строить уже не нужно, а для построения дороги достаточно соединить точку К' с точкой L. Точку пересечения отрезка К'L с берегом реки, прямой b, обозначим буквой Е. Если теперь выполнить параллельный перенос в противоположном направлении на длину отрезка K'K, то точка К' возвратится в исходное положение, а точка Е займет положение Е' на другом берегу реки. Отрезок К'Е займет положение КЕ'. Ломаная КЕ'ЕL будет кратчайшим расстоянием от точки К до точки L. Длина пути равняется сумме отрезков К'L и Е'Е.
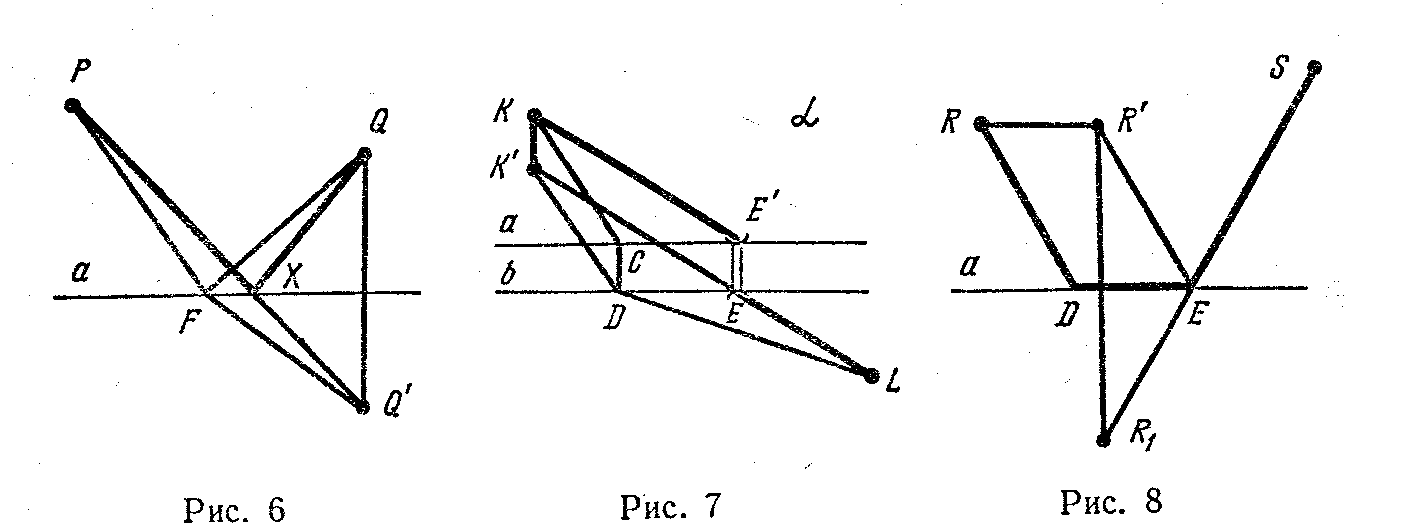
При любом другом положении моста, например при положении СD, путь из точки К в точку L будет длиннее (рис. 7), так как длина ломаной К'D+DL- больше отрезка К'L, следовательно, путь КСDL через мост СD будет длиннее, чем через мост Е'Е.
Задача 3. Перенесем точку R на расстояние RR'= т параллельно прямой а (рис. 8). Построим точку R1, симметричную точке R' относительно а. Соединим R1 с S. Получим точку Е пересечения отрезка R1S с прямой а. Тогда на основании первой задачи сумма R'Е+ЕS будет наименьшей. Выполним параллельный перенос точки R' в сторону R на расстояние ЕD=т. Тогда RD=R'Е и RD+DЕ+ЕS будет кратчайшим расстоянием от точки R до точки S с заездом на платформу DЕ.
Подводятся итоги объяснения решений задач.
После рассмотрения трех задач создается ориентировочная основа будущих действий по проектированию дороги.
В зависимости от того, как отвечали члены команд, каждая команда получает то или иное количество очков.
Задача учителя состоит в том, чтобы сохранить работоспособность и сплоченность внутри ПБ, учесть индивидуальные особенности в творчестве, направить работу отделов на выполнение основного задания.
На четвертом этапе учащиеся, обогащенные опытом решения частных задач и вооруженные ориентировочной основой действий, приступают к выполнению задания своего отдела.
Учитель напоминает, какие участки дороги должны быть спроектированы каждым отделом (рис. 5).
После того как учащиеся каждой команды выполнят построения в тетрадях, происходит защита проектов.
В большинстве случаев работу защищает «главный инженер» со своими ассистентами. Проектирование участка дороги, грамотность защиты оцениваются главным арбитром — учителем.
После создания проекта дороги и проведенной защиты подводятся итоги игры.
Рефлексия урока.
В общей сложности процесс решения инженерной задачи — проектирование дороги — расчленился на следующие этапы:
1) постановка инженерной задачи;
2) построение математической модели этой задачи;
3) актуализация необходимых знаний, решение задач, составляющих элемент общей задачи;
4) решение общей задачи на модели, составление проекта дороги;
5) проверка и корректировка решения, защита проекта;
6) реализация проекта в связи с другими ПБ;
7) оценка результатов решения (определение команды-победителя, выставление оценок в журнал);
8) анализ итогов работы.
В ходе деловой игры ученики не только повторяли пройденный материал, воспроизводили знания, но и творчески работали над созданием проекта дороги.
Специфическая форма игровой деятельности способствовала активизации учебного процесса по выработке навыков решения задач с помощью геометрических преобразований, выработке необходимой мотивации математической и инженерной деятельности.
Деловая игра «Конструктор»
На данном уроке учащиеся восьмых классов будут выступать в качестве конструкторов роботомеханизмов.
Тема: «Преобразование фигур на плоскости. Симметрия в природе и технике; Геометрические места точек» (VIII класс).
Учитель рассказывает, что детали роботомеханизма имеют форму геометрических фигур. В процессе выполнения роботом отдельных операций его детали перемещаются в пространстве и некоторых плоскостях. При создании роботов важно знать, какие траектории будут описывать определенные точки некоторых деталей при заданном движении других точек.
Организационная работа: класс делится на две команды — конструкторские бюро (КБ). Во главе каждого КБ стоит «главный инженер» (капитан команды), который выбирается участниками по согласованию с учителем.
Общие этапы игры:
1) Подготовительный этап. Проводится актуализация опорных знаний, которые будут использованы в процессе решения технической задачи.
2) Ознакомление учащихся с условием задач. После постановки задачи разрешаются консультации внутри КБ для выяснения подхода к решению задачи. Консультации могут быть групповыми и индивидуальными.
3) Первый этап решения задачи. На этом этапе каждый член КБ может решить предложенную математическую задачу для частных положений гипотенузы АВ (рис. 9) и отрезка РD (рис. 10).
4) Второй этап решения задачи. Теперь каждый ученик может решить задачу для общего положения отрезков АВ (рис. 11) и РD (рис. 12).
5) Обмен задачами и объяснение их решения. Для ответа у доски учащиеся вызываются «главными инженерами». Кандидатуры предлагаются не из своего КБ.
6) Подведение итогов работы. Побеждает то КБ, которое наберет наибольшее количество очков, и каждый «конструктор», который сможет аргументировано решить техническую задачу на базе математической.
Данный урок проводится в конце изучения темы «Преобразование фигур на плоскости» (VIII класс). К этому времени учащиеся уже знакомы с примерами преобразования фигур и их свойствами.
На уроке повторяется понятие ГМТ как фигуры, состоящей из всех точек плоскости, обладающих определенными свойствами. С помощью кодопозитива на доску проецируются простейшие ГМТ. Повторяются свойства равнобедренного треугольника, средней линии треугольника, признаки равенства прямоугольных треугольников.
Решаются следующие задачи (без записи в тетрадях):
1. Построить точку М, равноудаленную от сторон данного угла и от данных двух точек А и В.
2. Найти ГМТ середин всех хорд данной окружности, которые выходят из одной точки этой окружности.
Учитель подводит итоги работы двух команд в процессе актуализации опорных знаний и решения задач. Итоги подготовительного этапа в баллах записываются на доске.
Далее для каждого КБ формулируется конструкторская задача.
Задача для I КБ.
Основанием подвижной части роботомеханизма является равнобедренный треугольник АВС (АСВ=90°) который перемещается в плоскости так, что его вершины A и В скользят по сторонам прямого угла МОN(МОN=90°). Известно, что АС=ВС==а и МО=ОN=АВ. Какую траекторию опишет точка С, вершина прямого угла треугольника АВС, если точка А опишет отрезок ОМ, а точка В—отрезок ОN (рис. 9)?
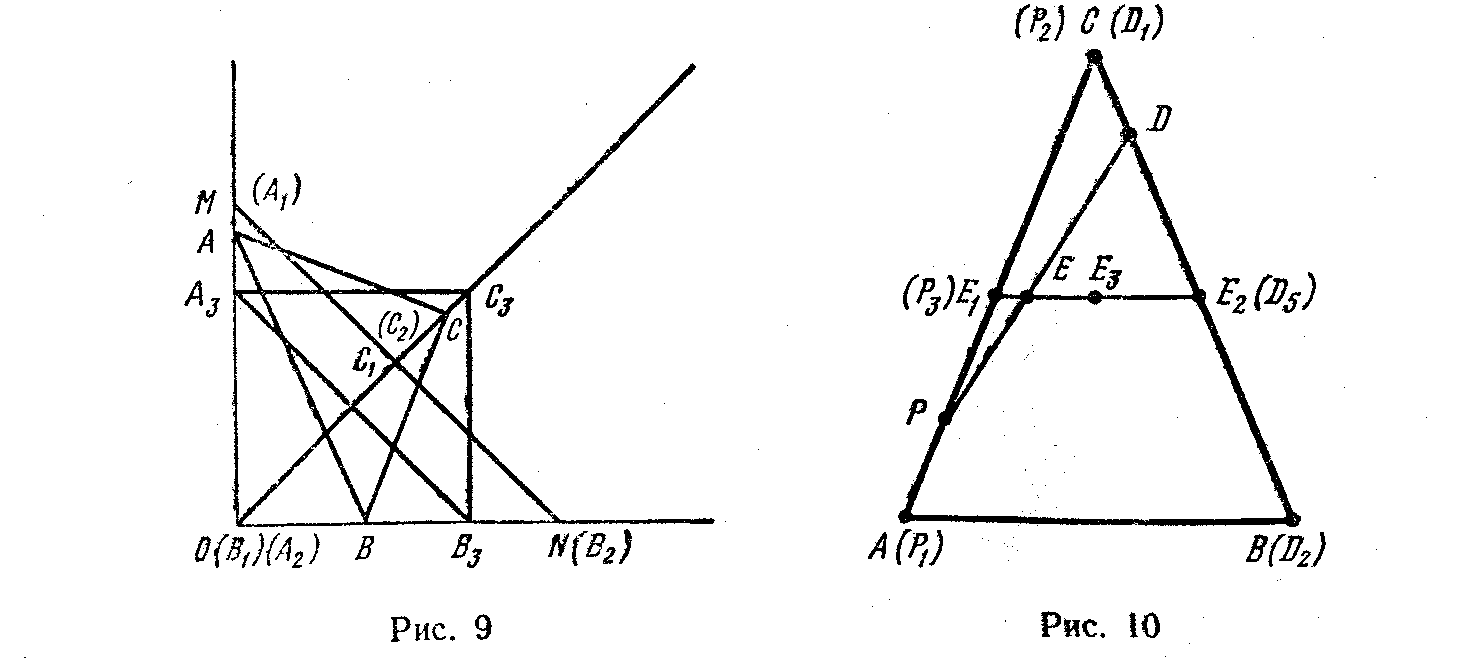
Задача для II КБ. Концы Р и D отрезка переменной длины подвижной части роботомеханизма скользят по сторонам равнобедренного треугольника АВС (АС=ВС) так, что расстояния АР и СD все время одинаковы. Найти фигуру, которую опишут середины всех отрезков РD (рис. 10).
Первый этап решения задачи.
Учащиеся каждой команды изучают условие задачи, выполняют рисунки. Капитаны команд следят за тем, чтобы каждый ученик сделал рисунок в тетради и мог объяснить его для определенных положений треугольника АВС (рис. 9) и отрезка РD (рис. 10).
В это время возможны консультации внутри КБ, а также консультации со стороны учителя.
Через некоторое время «главные инженеры» КБ объявляют о возможности начать опрос.
К доске идут отвечать ученики из первого КБ по предложению «инженеров» второго КБ и наоборот. Это значит, что руководитель и все члены КБ должны быть уверены за своего «сотрудника» и знать, что он их не подведет. А это, в свою очередь, требует внимательности и ответственности от каждого ученика в период подготовки и умения ответить на вопрос.
Дополнительно два балла засчитывается тому КБ, которое первым дало согласие на фронтальный опрос и опрос у доски.
Вызванные к доске ученики выполняют рисунки для отдельных положений детали роботомеханизма (треугольника АВС в первой задаче и отрезка РD — во второй).
Приводим примерный ответ ученика из первого КБ:
Пусть С1 — положение вершины С в момент, когда точка А совпадает с точкой М, а точка В — с точкой О, имеем треугольник А1С1В1 (рис. 9). Понятно, что точка С лежит на биссектрисе угла МОN. Аналогичную картину имеем, когда треугольник АВС занимает положение А2С2В2. Если ОВз=ОАз, то вершина С треугольника АВС займет положение Сз на биссектрисе угла МОN. Остается рассмотреть общий случай, когда ОАОВ (рис. 11).
Примерный ответ ученика из второго КБ:
Если концы отрезка переменной длины РD совпадают с вершинами А и С (Р1 с А1, D1 с С), то серединой отрезка РD будет точка Е1(Е1А=Е1С) (рис. 10). Аналогично: если концы отрезка РD совпадают с вершинами В и С (P2 с С, D2 с В), то серединой РD будет точка Е2(СЕ2=ВЕ2). В случае когда Р совпадает с Е1 и D с Е2, серединой отрезка РD будет точка E3. Остается рассмотреть общий случай, когда АР=СD, АР0, СD0 и АР=СDАЕ1 (рис. 12).
Учащиеся обоих КБ следят за ответами товарищей, так как по правилам игры произойдет обмен задачами между КБ.
Второй этап решения задач.
В обоих КБ выполняются рисунки для общего положения треугольника АВС (рис. 11) и отрезка РD (рис. 12). Обсуждаются идеи решения задачи. Возможны консультации внутри команд. Через некоторое время «главные инженеры» докладывают о готовности КБ к ответу. Отвечающие у доски ученики выбираются по тому же принципу.
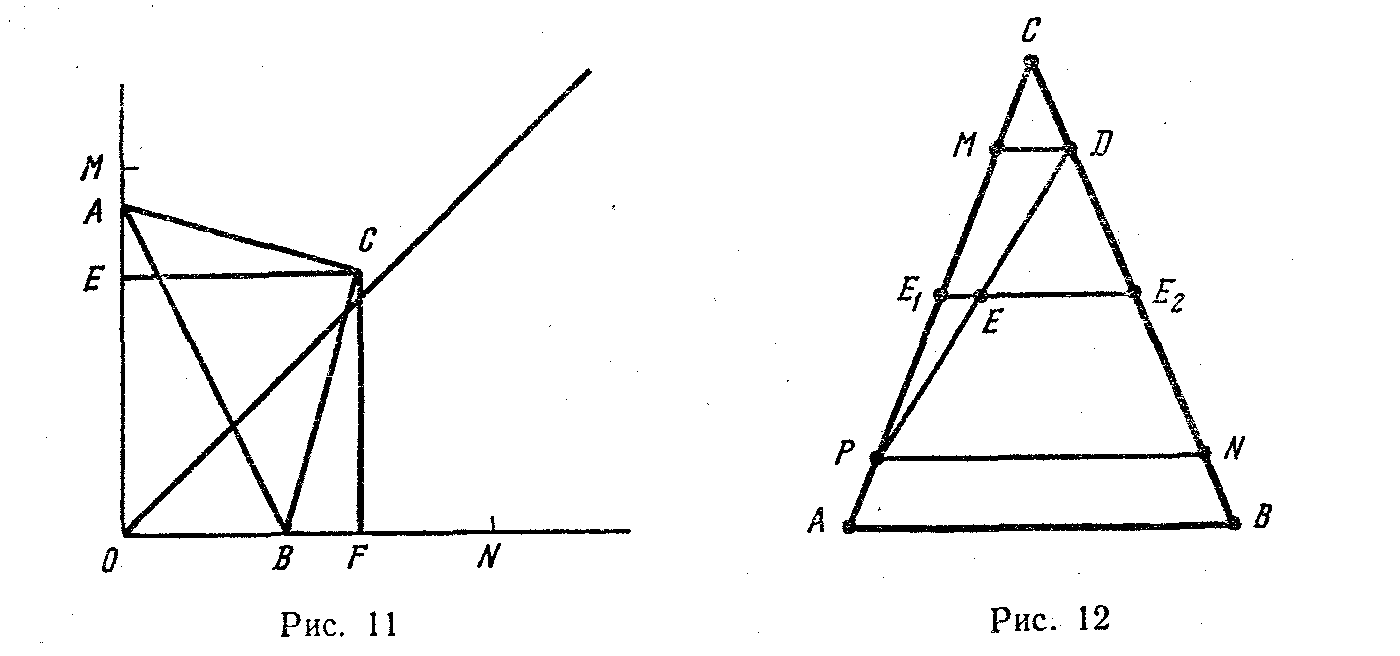
Примерный ответ ученика из первого КБ:
Пусть теперь треугольник AВС занимает произвольное из допустимых его положений (рис. 11). Опустим из точки С перпендикуляры СF и СЕ на ОN и ОМ соответственно, тогда ВСF=АСЕ, как острые углы с соответственно перпендикулярными сторонами. Кроме того, АС=ВС по условию. Отсюда следует, что AEС=ВСF, и поэтому СЕ=СF, так что точка С и в этом случае лежит на биссектрисе угла МОN. Получаем, что ГМТ вершины С будет отрезок С1С3 (рис. 9).
Примерный ответ ученика из второго КБ:
Пусть отрезок РD занимает одно из допустимых его положений (рис. 12). Через точки Р и D проведем DМ//РN//АВ. Тогда СМ = СD = РА = NВ и РЕ1=Е1М. Средняя линия Е1Е2 треугольника АВС совпадает со средней линией треугольника РМD. Получаем, что середина отрезка РD в любом его положении лежит на средней линии Е1Е2, треугольника АВС. Следовательно, ГМТ середины отрезка РD будет средняя линия Е1Е2.
Если из обеих команд последовали существенные дополнения, они, как и прежде, оцениваются дополнительными баллами.
Подводятся итоги второго этапа решения задач. Результаты записываются на доске.
После этого ведущий игры предлагает обменяться задачами.
Повторно зачитываются условия для каждого КБ.
Вновь акцентируется внимание на конструировании робототехники.
На обдумывание задачи, выполнение рисунков и записи решения отводится минимум времени. Возможны консультации внутри команды.
Только после того как у руководителя КБ появляется уверенность в том, что каждый ученик сможет объяснить задачу, дается согласие на ответ.
Дополнительные баллы получает то КБ, которое первым пришло к готовности. Как и в первом случае, объяснение решения задачи проходит в два этапа. Дополнения к ответам приносят командам дополнительные баллы.
Подводятся итоги работы.
Учитель проверяет записи в тетрадях. Учитываются хорошо проведенные индивидуальные консультации. Ученики, отвечавшие у доски и с места, получают оценки в журнал.
На заключительном этапе работы высказываются также предположения о возможности применения рассмотренных роботомеханизмов на производстве.
Рефлексия урока.
На основании рассмотренных примеров отметим, что для проведения деловых игр в классе существенными являются следующие факторы: математическая подготовка учащихся класса, понимание ими цели и механизма игры, заинтересованность их в получении результатов, оперативность проведения игры, возможность оценки учениками своих действий, а также наличие опытного и понимающего нюансы игры ведущего — учителя математики.
Перечислим основные требования, на которые следует ориентироваться при подготовке и проведении деловой игры в классе:
1. Описываемые производственно-технические задания или ситуации должны соответствовать задаче исследования и быть достаточно простыми, чтобы учащиеся хорошо понимали цель игры и способы достижения результатов.
2. Учитель математики — ведущий игры — должен четко представлять все особенности моделируемой ситуации, уметь быстро проверять полученные при решении задач результаты и интерпретировать их согласно производственной задаче.
3. Игра должна проводиться оперативно. Нельзя допускать потери интереса к игре и утомления учеников. Для поддержания интенсивной работы во время игры надо предусмотреть способы стимулирования учащихся, отмечать в процессе игры наиболее отличившихся, подбадривать отстающих.
4. В процессе игры нужно учитывать факторы, порождающие конкретные ситуации, а также то, что на «выигрыш» команды или ученика оказывают влияние действия не только отдельных учеников, но и всего коллектива.
Применение дидактических игр и имитаций в процессе обучения математике осуществляется в различных формах. Одной из них является математическое моделирование.
Математическое моделирование, как правило, предполагает имитацию различных ситуаций математическими средствами.
Вспомним известную игру в «магазин». В процессе купли-продажи дети манипулируют некоторыми предметами, вкладывая в каждый из них определенный смысл.
Таким образом, без всякого принуждения извне они совершают чрезвычайно важную операцию: придают предметам различные значения.
Дидактическая особенность этой способности детей становится понятной, если учесть, что при построении различных моделей аксиоматической теории также приходится отвлекаться от обычного смысла, вкладываемого в исходные понятия теории, перестраиваться на новый смысл этих понятий, соответствующий той или иной конкретной модели.
Приведем примеры имитаций при математическом моделировании.
Тема: «Логическое строение геометрии и аксиоматический метод в математике» (IX класс).
Вначале учащимся разъясняются отмеченные выше особенности игры в «магазин».
По аналогии с этой игрой предлагается игра математического содержания.
Точками в рамках этой игры будем считать цифры 1, 2, 3. Под прямыми будем понимать пары, составленные из двух цифр: (1 ; 2), (1 ; 3), (2 ; 3).
Отношение «точка принадлежит прямой» будет означать наличие цифры в паре цифр. Например, точка 1 принадлежит прямой (1 ; 3) и не принадлежит прямой (2;3).
Цель задания заключается в том, чтобы проверить, будут ли выполняться аксиомы принадлежности при таком истолковании точек и прямых (Погорелое А. В. Геометрия, 7—11 класс.—М.: Просвещение, 1989).
Основные свойства принадлежности точек и прямых:
I1. Какова бы ни была прямая, существуют точки, принадлежащие ей, и точки, не принадлежащие ей.
I2. Через любые две точки можно провести прямую, и только одну.
Выполнение первой аксиомы в нашей модели очевидно. Для прямой (1 ; 2) точки 1 и 2 принадлежат ей, а точка 3 не принадлежит.
Вторая аксиома тоже справедлива. Точкам 1 и 2 соответствует прямая (1;2), и только одна. Точкам 1 и 3 соответствует прямая (1 ; 3), точкам 2 и 3 — прямая (2 ; 3).
Формулировки аксиом I1 и I2 в рассматриваемой модели будут такими:
I1. Для любой пары цифр (1;2); (1;3); (2; 3) существуют цифры, взятые из тройки цифр (1 ; 2 ; 3), принадлежащие этим парам и не принадлежащие им.
I2. Для любых двух цифр из тройки цифр (1 ; 2 ; 3) существует одна, и только одна, пара цифр, содержащая их.
Рассмотрим еще один пример имитации.
Возьмем квадрат.
Под прямыми будем понимать стороны квадрата и его диагонали, под точками — вершины квадрата. В данном случае моделью будет совокупность четырех вершин квадрата А, В, С, D и шести отрезков АВ, АС, АD, ВС, ВD, СD. Точка О пересечения диагоналей квадрата в пределах данной модели не является точкой.
Проверим выполнение аксиом.
I1. Для любой стороны и диагонали квадрата существуют вершины квадрата, принадлежащие и не принадлежащие им.
I2. Через две любые вершины квадрата можно провести его сторону или диагональ, и притом только одну.
Рассмотрим одну из теорем в нашей теории.
Теорема. Две различные прямые либо не пересекаются, либо пересекаются только в одной точке.
Пересекающимися прямыми в нашей модели будут А В и АD, ВС и СD, ВС и АС и т. д. Непересекающимися будут АВ и СD, АD и ВС. Необходимо обратить внимание учащихся на прямые АС и ВD. В данной интерпретации они не пересекаются. Полезно также обратить внимание на следующий факт: если какое-либо предложение не выполняется в рамках данной модели, то это предложение не может быть получено как следствие из аксиом данной теории. Так, например, предложение «Существуют вершины квадрата, через которые проходит по крайней мере одна сторона, параллельная данной стороне» не может быть доказано на базе аксиом I1, I2.
В дальнейшем построении теории возможны две ситуации: либо это предложение принять за аксиому, либо пополнить список аксиом такими предложениями, на основе которых можно было бы осуществить доказательство данного предложения.
Таким образом, рассмотрение данной игры послужило важным эвристическим средством, подсказывающим направление дальнейшего развития теории.
Рассмотрим еще один пример.
Тема: «Декартовы координаты на плоскости» (VIII класс).
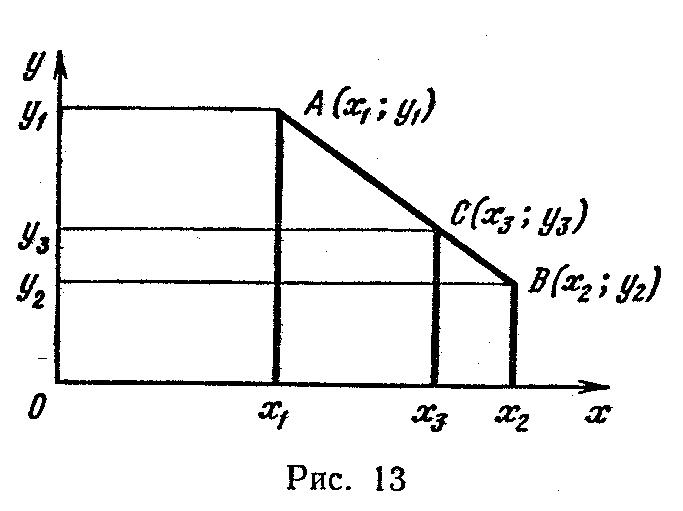
Под точками будем понимать пары чисел (х; у). Под расстоянием от точки А (х1; у1) до точки В (х2; у2) будем понимать наибольшее из чисел /х2—х1/ и /у2—у1/; АВ=тах(/х2—х1/, /у2—у1/).
Убедимся в том, что такая имитация расстояний возможна. Рассмотрим аксиомы расстояний (Погорелов А. В. Геометрия, 7— 11 класс.—М.: Просвещение, 1989).
III1. Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Выполнение аксиомы III1 можно проследить на рисунке 13. В данном случае расстоянием между точками A и B (длина отрезка АВ) будет /х2—х1/, большее из чисел /х2—х1/ и /у2—у1/.
Разобьем отрезок АВ на две части точкой С. Тогда:
АС=тах(/х3—х1/, /у3—у1/)=/х3—х1/.
СВ=тах(/х2—х3/, /у2—у3/)=/х2—х3/.
АС+СВ=/х3—х1/+/х2—х3/=/х2-х1/=АВ.
Большой интерес учащихся вызывают имитации некоторых геометрических образов: отрезка, луча, прямой. Рассматривая эти случаи, учащиеся убеждаются в том, что отрезок может быть имитирован произвольным прямоугольником. (За длину отрезка принимается площадь прямоугольника. Тогда каждому отрезку - прямоугольнику соответствует определенная длина-площадь. И сумма длин частей отрезка - прямоугольника, на которые он разбивается любой его точкой-прямой, равна длине - площади самого отрезка-прямоугольника.)
Приведенные примеры различных моделей отрезков, удовлетворяющих аксиомам метрики, вынуждают учащихся «посмотреть» на понятие отрезка с позиции аксиоматического метода. Учащиеся убеждаются в том, что отрезки, удовлетворяющие аксиомам метрики, могут значительно отличаться по своему «внешнему» виду и по своим свойствам от обычных отрезков. Естественно, напрашивается мысль, что необходимо введение дополнительных ограничений (посредством аксиом), которые позволили бы исключить такие «необычайные» случаи. Так что введение новых аксиом становится мотивированным. Примечательно, что выяснение особенностей рассмотренной модели не только оправдывает введение новых аксиом, но и подсказывает их содержание.
Систематическое применение различных моделей отдельных групп аксиом в процессе выполнения заданий - игр позволяет подвести учащихся к пониманию сущности полуформальной аксиоматической теории в отличие от содержательной, в которой понятия об основных ее объектах получают однозначное, конкретное истолкование. При этом обычные наглядные представления учащихся об исходных понятиях геометрии остаются. Новые истолкования основных понятий действуют лишь в процессе игры и не выходят за ее рамки.
Итак, деловые игры следует использовать при изучении математики. Важное условие их эффективности — профессиональная направленность решаемых задач и их проблемность, а также рациональное сочетание коллективных и индивидуальных действий участников игры.
