Учебно-методический комплекс для специальностей 030501 Юриспруденция 032700 Юриспруденция
| Вид материала | Учебно-методический комплекс |
СодержаниеТиповые билеты |
- Учебно-методический комплекс Для специальностей: 030501 юриспруденция Москва 2008, 721.07kb.
- Учебно-методический комплекс форма обучения очно-заочная Специальность 030501 «Юриспруденция», 2016.02kb.
- Учебно-методический комплекс Для специальностей: 032401 «Реклама» 030501 «Юриспруденция», 1105.01kb.
- Одобрено учебно-методическим советом юридического факультета финансовое право учебно, 2268.04kb.
- Учебно-методический комплекс Для специальностей: 030501 Юриспруденция 080801 Прикладная, 498.9kb.
- Учебно-методический комплекс по направлению: 030500 «Юриспруденция» по специальности:, 405.38kb.
- Учебно-методический комплекс по направлению: 030500 «Юриспруденция» по специальности:, 427.52kb.
- Учебно-методический комплекс по направлению: 030500 «Юриспруденция», по специальности:, 549.14kb.
- Учебно-методический комплекс по направлению: 030500 Юриспруденция, по специальности:, 715.55kb.
- Учебно-методический комплекс по направлению: 030500 «Юриспруденция» по специальности:, 264.54kb.
ТИПОВЫЕ БИЛЕТЫ
ТИПОВОЙ БИЛЕТ 1 (комплект МИЮ12-01)
| | Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что в каждом числе нет одинаковых цифр? | ||||||||||
| | Вычислить: P5(P4 - P3). | ||||||||||
| | В урне 9 белых и 6 черных шаров. Из урны вынимают два шара. Какова вероятность того, что оба шара окажутся белыми? | ||||||||||
| | В коробке имеется 15 шаров, из которых 10 – окрашены, а 5 – прозрачные. Извлекаем, не глядя, 3 шара. Какова вероятность того, что все они будут окрашены? | ||||||||||
| | В результате пяти измерений длины стержня одним прибором получены следующие результаты (в мм) 96;98;103;108;110. Определить несмещенную оценку длины стержня | ||||||||||
| | Для выборки, заданной распределением, найти выборочные среднюю, дисперсию и стандарт.
| ||||||||||
| | Если А = {4,5,6,7}, В = {10,11,12,13}, то S = AÈB = | ||||||||||
| | Пусть А = {0,2,4,6,8}, В = {-2,0,4,8}. Найти AÈB, AÇB, A \ B, B \ A. | ||||||||||
| | Проверить, является ли следующая формула тождественно истинной, не тождественно истинной или тождественно ложной:  . . | ||||||||||
| | Проверить, является ли следующий предикат тождественно истинным или не тождественно истинным: 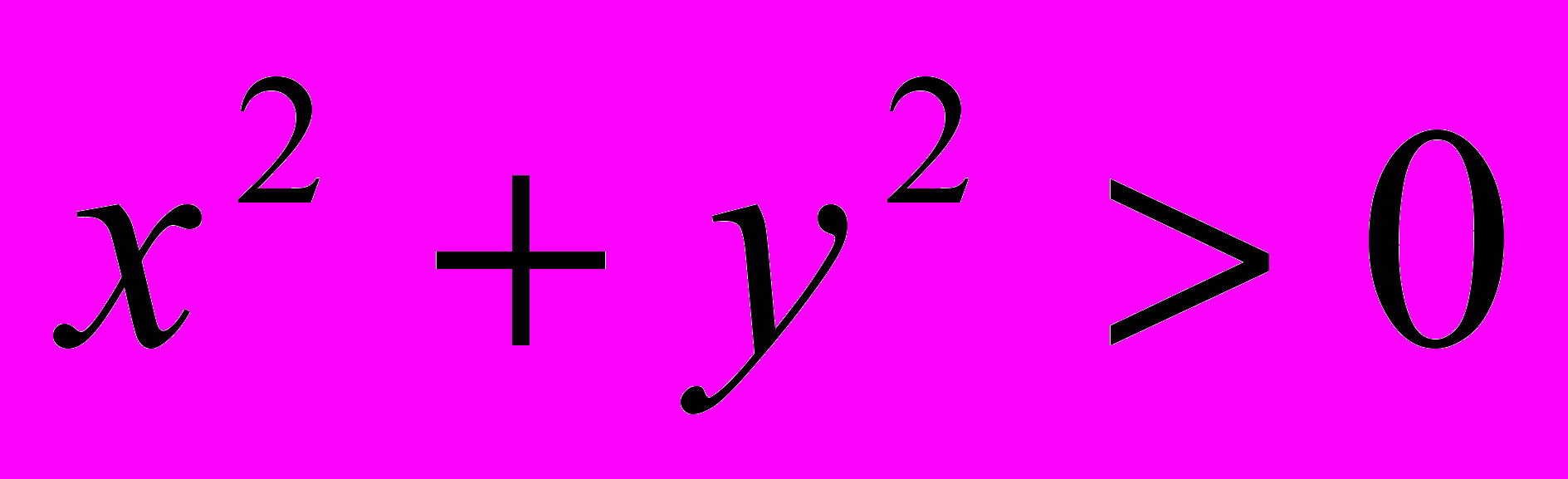 . . | ||||||||||
| | |||||||||||
ТИПОВОЙ БИЛЕТ 2 (комплект МИЮ12-01)
| | Вычислить 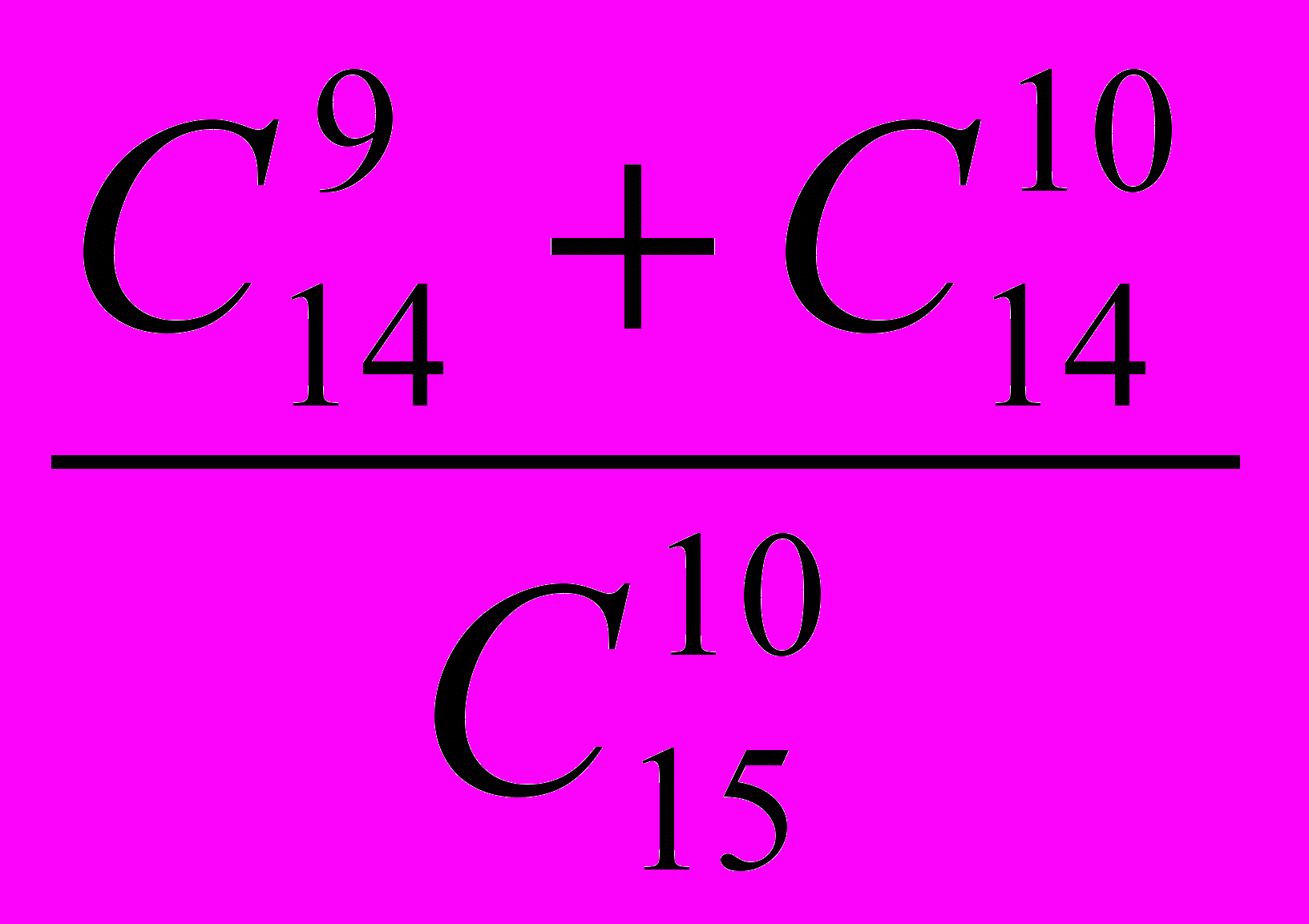 . . | ||||||||||||||
| | Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что в каждом числе нет одинаковых цифр? | ||||||||||||||
| | Найти числовые характеристики случайной величины х, заданной законом распределения
| ||||||||||||||
| | В первом ящике 2 белых и 10 черных шаров, во втором 8 белых и 4 черных. Из обоих ящиков вынули по шару. Определить вероятность того, что оба шара будут белыми. | ||||||||||||||
| | Найти статистические характеристики выборки, извлеченной из генеральной совокупности.
| ||||||||||||||
| | Составить распределение относительных частот и построить полигон относительных частот по заданному распределению частот выборки.
| ||||||||||||||
| | Пусть А – множество точек круга единичного радиуса с центром в начале координат; В – множество всех точек координатной плоскости. Изобразить множества AÈB, AÇB, A \ B, B \ A. | ||||||||||||||
| | Пусть А = {0,2,4,6,8}, В = {-2,0,4,8}. Найти AÈB, AÇB, A \ B, B \ A. | ||||||||||||||
| | Построить таблицу истинности для высказывания 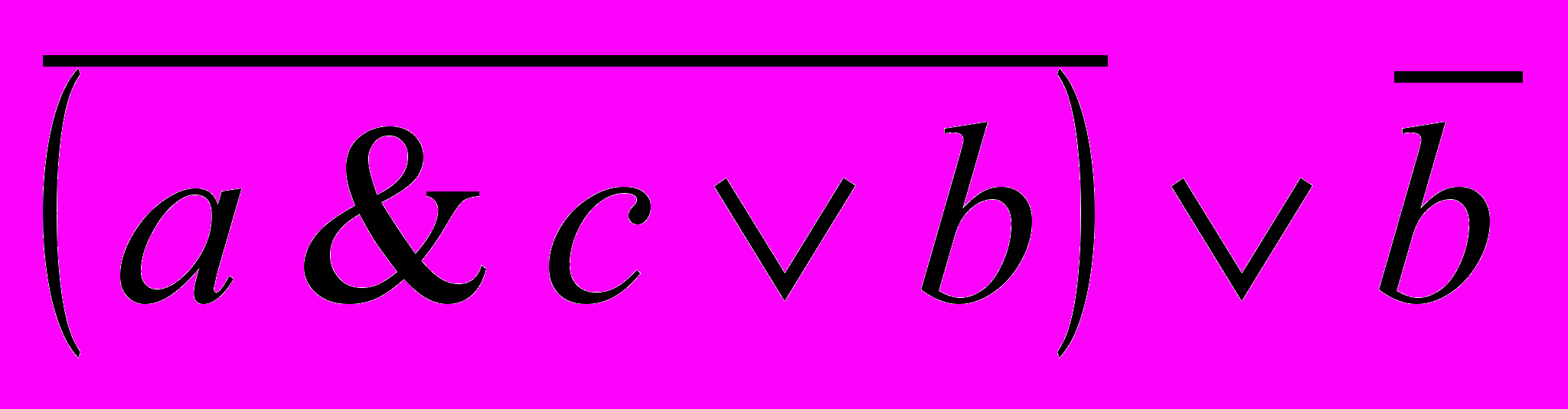 . . | ||||||||||||||
| | Найдите логические значения x и y, при которых выполняется равенство 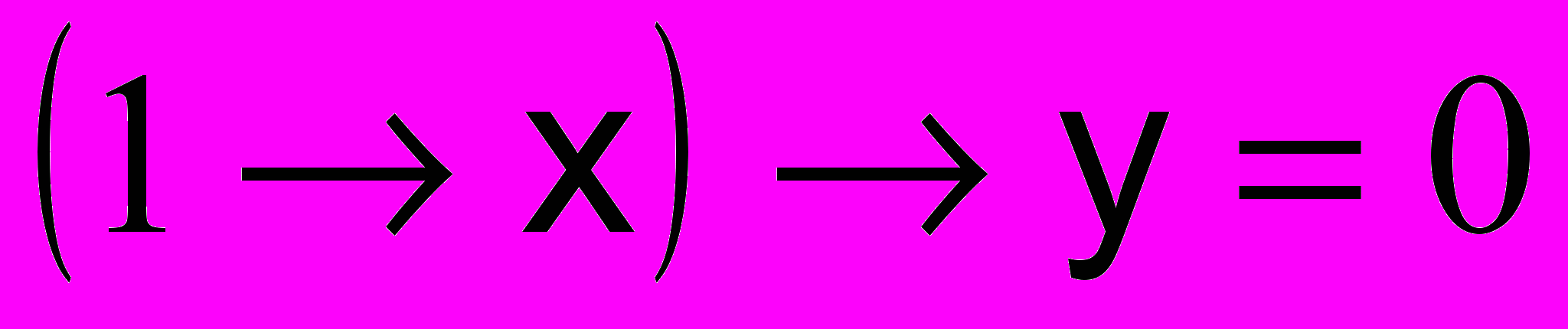 | ||||||||||||||
| Зав. кафедрой _________________ | |||||||||||||||
