Geum.ru

Сердюк А. М., Останина Н. В., Кузнецова Е. М., Череменко А. Н., Босых Ю. С., Брязкало В. В., Олейник И. Л

Вид материалаДокументы

Содержание


Митько Л. А.
Подобный материал:
1   ...   5   6   7   8   9   10   11   12   ...   38

КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ФИЗИКО-ХИМИЧЕСКИХ ПРОЦЕССОВ В ПРИЗЕМНОМ СЛОЕ АТМОСФЕРЫ – НЕОБХОДИМЫЙ КОМПОНЕНТ ИНФОРМАЦИОННОГО ОБЕСПЕЧЕНИЯ В СИСТЕМЕ ЭКОЛОГО-ГИГИЕНИЧЕСКОЙ БЕЗОПАСНОСТИ

Митько Л. А.

Украина, Киев, Институт проблем моделирования в энергетике НАН Украины


Проблема охраны окружающей среды и ее восстановление становится одной из важнейших задач науки, развитие которой стимулируется все возрастающими темпами технического прогресса во всех странах мира. Бушующее развитие промышленности способствовало появлению перед человечеством острой проблемы – сохранение экологических систем, которые исторически сформировались на нашей планете.

В последние десятилетия экологические системы испытают значительное влияние природных и, в особенности, антропогенных факторов, изменяясь в нежелательном для человечества направлении. Поэтому прогноз изменения экологических систем вследствие указанных причин является актуальной задачей, решение которой состоит из двух этапов:

а) исследование процесса загрязнение окружающей среды выбросами отходов промышленных предприятий и вследствие катастрофических явлений антропогенного и природного происхождение;

б) оценки влияния вредных загрязнений на ноосферу.

Важной составной этой задачи есть проблема оценки загрязнение атмосферы и земной поверхности пассивными и активными примесями. Примесь называется пассивной, если она не испытает физико-химические изменения вплоть до выпадения на поверхность земли. Если же она в процессе распространения в атмосфере вступает в химические реакции с паром и другими компонентами атмосферы, вследствие чего переходит от одного химического состояния к другому, изменяя при этом характер токсичности по отношению к окружающей среде, то такая примесь является активной.

Процесс распространения промышленных выбросов и продуктов катастрофических явлений в атмосфере происходит вследствие их адвентивного перенесение воздушными массами и диффузии, которая предопределяется турбулентными пульсациями воздуха. Если примесь представляет собой совокупность грубых частичек, то, распространяясь в атмосфере, эти частички под действием силы тяготения падают на поверхность земли с определенной постоянной скоростью в соответствии с законом Стокса. Естественно, что почти все примеси в конечном итоге оседают на земной поверхности, причем тяжелые оседают в основном вследствие действия гравитационного поля, а легкие – вследствие диффузного процесса. Гравитационный поток тяжелых частичек является более интенсивным, чем диффузный, для легких же частичек - практически несущественный. Следует заметить, что наиболее опасными для окружающей среды являются газообразные примеси типа окислов.

Выявление тенденций загрязнения окружающей среды, как в определенный момент времени, так и за период времени, от источников загрязнения приземного слоя атмосферы представляет собой значительный интерес при решении различных проблем, имеющих отношение к эколого-гигиенической безопасности. Здесь особое место занимает задача прогнозирования процессов загрязнения атмосферы на определенный период упреждения. Но не менее важной является и задача определения загрязнения приземного слоя атмосферы за определенный прошедший период.

Исследование физических и химических процессов в приземном слое в большинстве случаев не позволяет проводить натурный эксперимент. Поэтому большое значение приобретает возможность проведения вычислительного эксперимента, для которого необходимо построение математических моделей, достаточно адекватных исследуемым природным процессам и реализуемых на современной вычислительной технике. На сегодня четко прослеживается необходимость создания информационной системы, одним из компонентов наполнения которой были бы данные, полученные в результате имитационного моделирования распространения вредных веществ в атмосфере в результате деятельности источников выбросов.

Исходной информацией для разработки математических моделей является оперативная информация о загрязнении (выборка данных, представляющих собой замеры концентрации загрязняющих веществ в местах установки контрольно-измерительных станций), метеопараметры (скорость ветра в приземном слое, направление ветра), а также данные, которые определяют структуру поверхности, температуру, физико-химические параметры загрязняющих веществ, различные коэффициенты.

Существует проблема построения математических моделей, позволяющих достаточно адекватно описывать распространение примесей. Особенно сложно создавать модели, которые могли бы моделировать распространение примесей на средние расстояния 100-500 км. Для таких моделей требуется создание специальных алгоритмов численной реализации, дающих возможность проводить вычислительные эксперименты одновременно в сотнях тысяч точек.

Рассмотрим один из вариантов построения математической модели распространения примеси в приземном слое атмосферы.

Задача расчета концентрации q(x,y,z,t) загрязнений в атмосфере вследствие их выброса и переноса может быть представлена в виде краевой задачи для уравнения 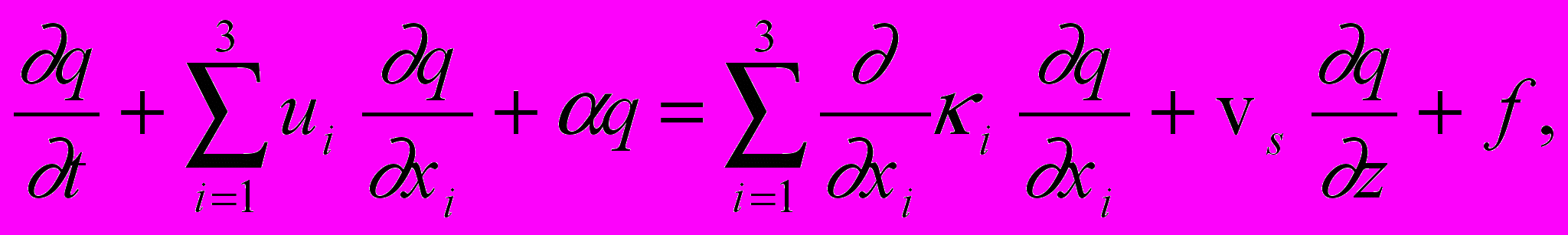[1]:

(1)

где (x1,x2,x3)=(x,y,z) – декартовы координаты, плоскость XOY которых соответствует земной поверхности, t – временная координата, (u1,u2,u3) – компоненты поля ветра,  – коэффициент распада вещества, учитывающий химические превращения вещества и вымывание его частиц осадками, i – коэффициенты турбулентного переноса, 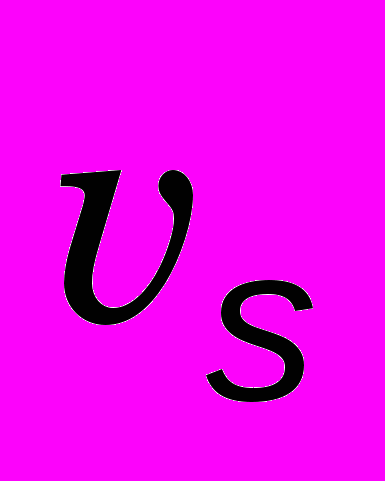– установившаяся скорость гравитационного оседания частиц вещества, f=f(x,y,z,t) – известная функция, описывающая плотность распределения источников загрязнения.

Начальные условия обычно формулируются в виде известной концентрации вещества в исследуемой области при t=0:

q(x,y,z,0)= q0(x,y,z). (2)

Краевые условия, во-первых, должны правильно отражать исследуемый процесс, а во-вторых, обеспечивать корректность поставленной задачи. Для решения рассматриваемой задачи, область исследования ограниченная, то есть имеет, например, вид параллелепипеда: 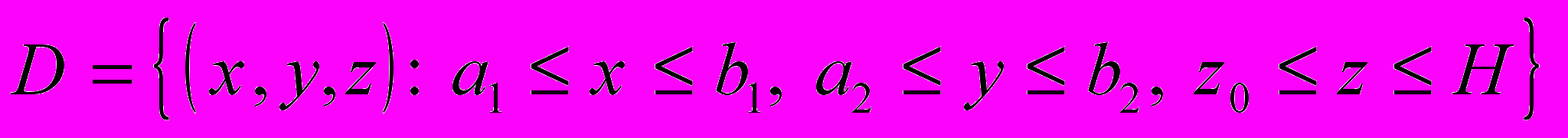. На боковых границах

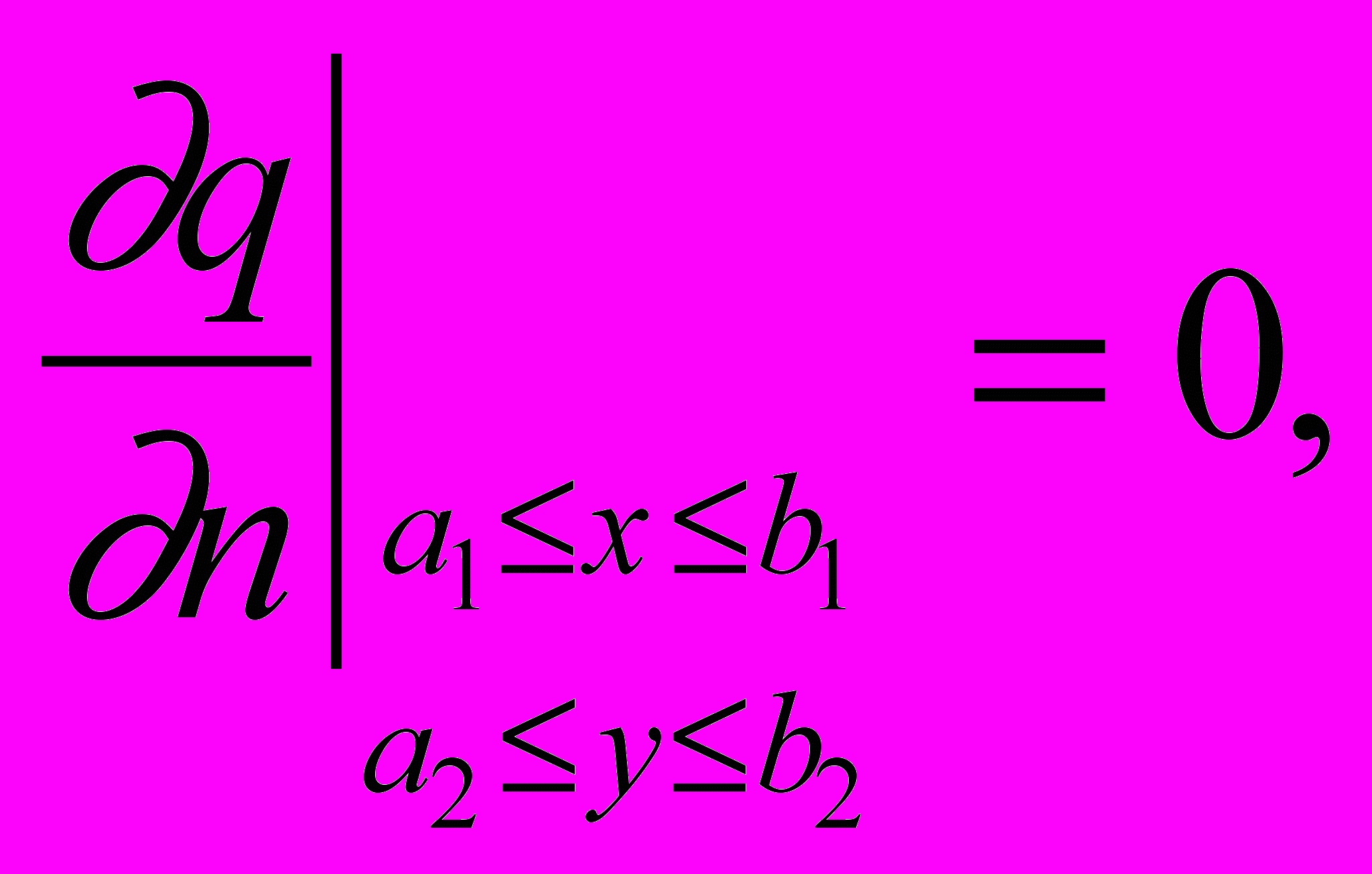(3)

На верхней границе области возможно моделирование различных процессов:

- равенство нулю концентрации вещества:

- отсутствие диффузионного переноса при условии, что вертикальная составляющая скорости воздуха равна нулю:



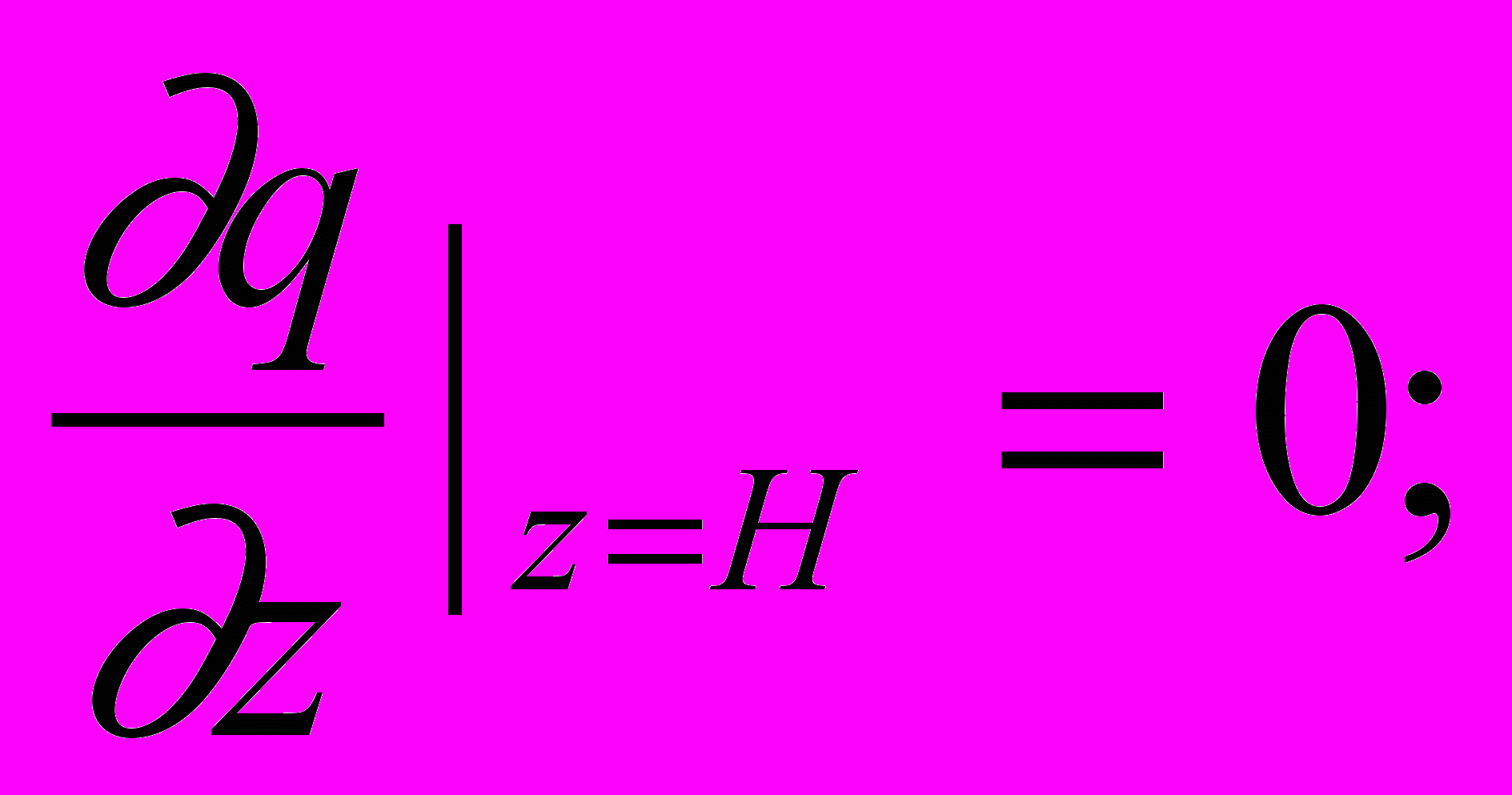
- наличие потока вещества через верхнюю границу:

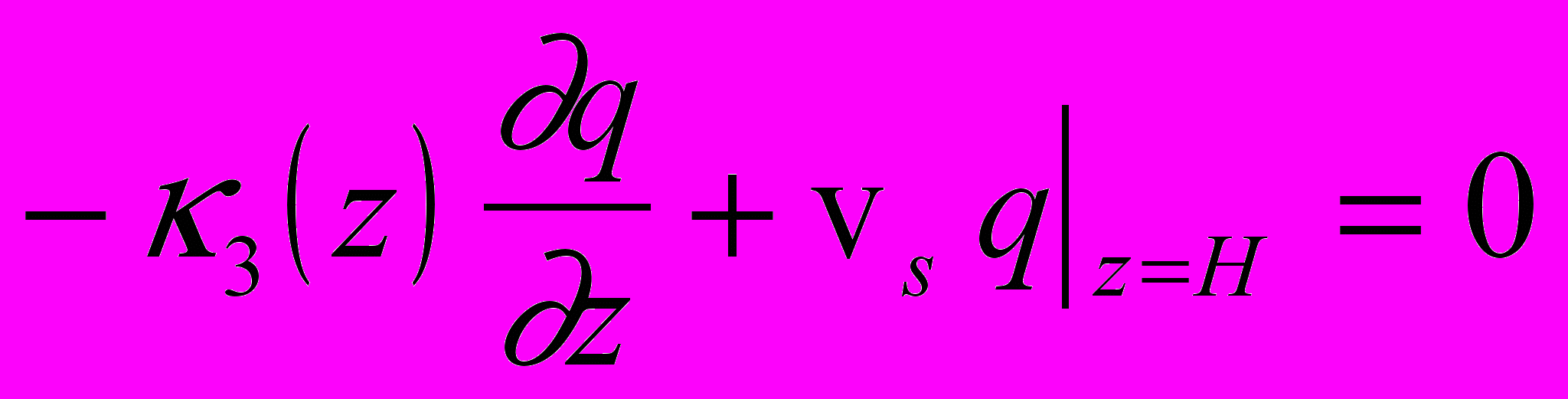(4)

Процессы, происходящие на подстилающей поверхности, также можно моделировать различным образом. Например, в [1] считается, что обычно примеси слабо взаимодействуют с поверхностью почвы и, попав на нее, не накапливаются, а с турбулентными вихрями снова уносятся в атмосферу. Поскольку такие вихри у поверхности невелики, то можно положить:

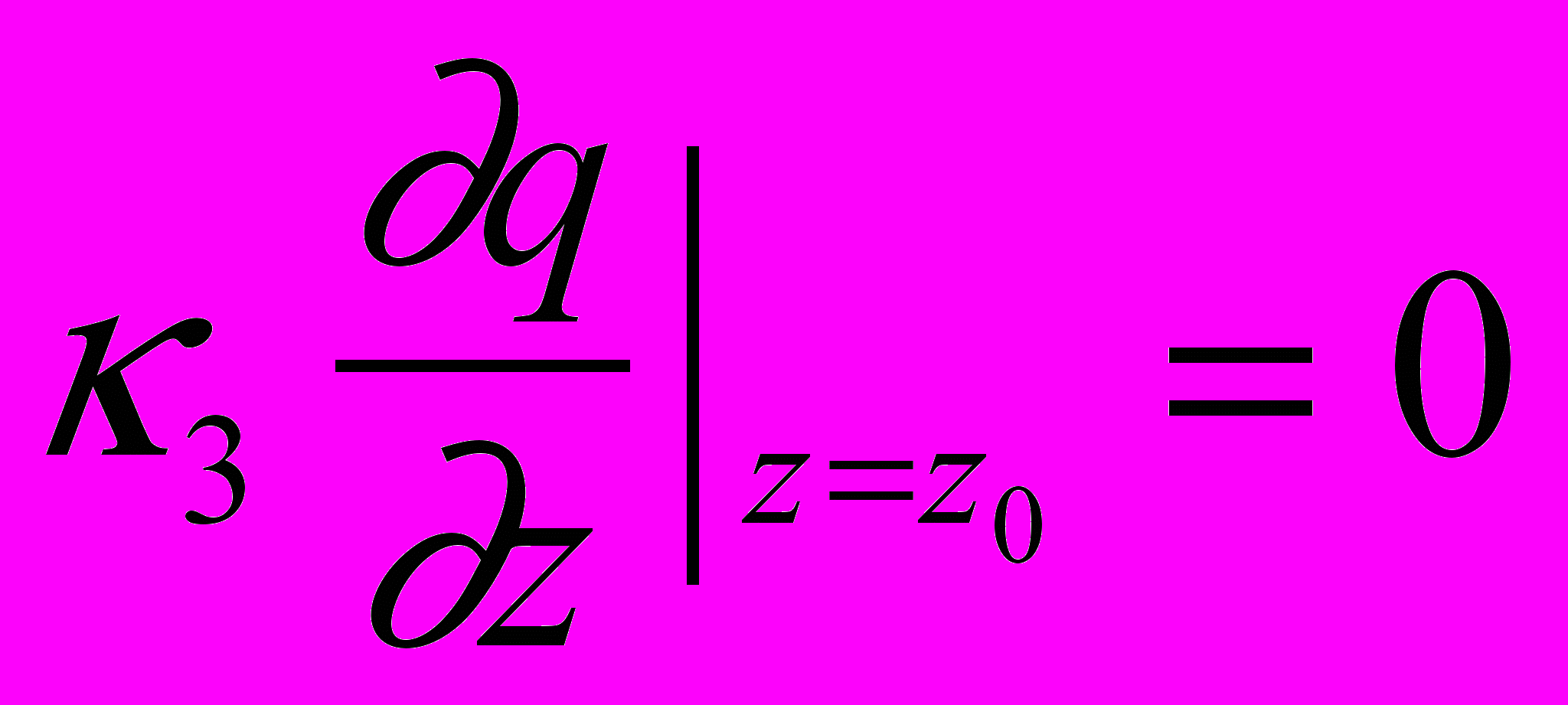. (5)

Однако при моделировании таких процессов как формирование пятен повышенной концентрации примеси на подстилающей поверхности, вторичный подъем и осаждение частиц условие (5) становится неудовлетворительным. В [2] предлагается такое условие на подстилающей поверхности:

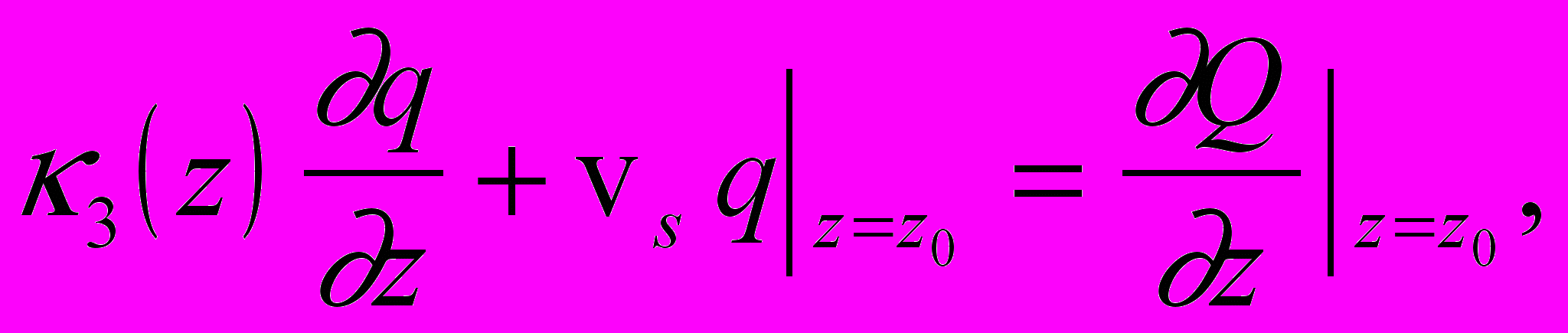(6)

где Q(x,y,t) – концентрация наземного поля примеси, z0=z*+z, z* – уровень шероховатости, z – толщина слоя сальтации. Поскольку эта концентрация может меняться во времени, то условие (6) дополняется соотношением

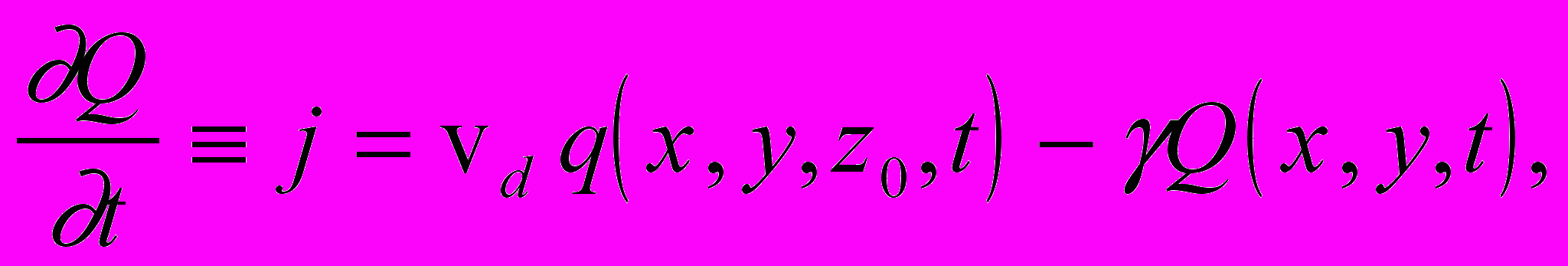(7)

где 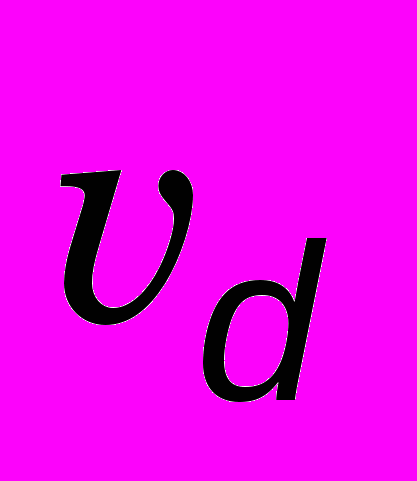– скорость сухого оседания примеси;  – интенсивность ветрового подъема. Использование условий (6), (7) требует, в свою очередь, задания начальной концентрации примеси на поверхности:

Q(x,y,0) = Q0(x,y). (8)

Если подстилающая поверхность представляет собой зеркало водного пространства, то, предполагая, что вода поглощает все примеси, получаем краевое условие

.

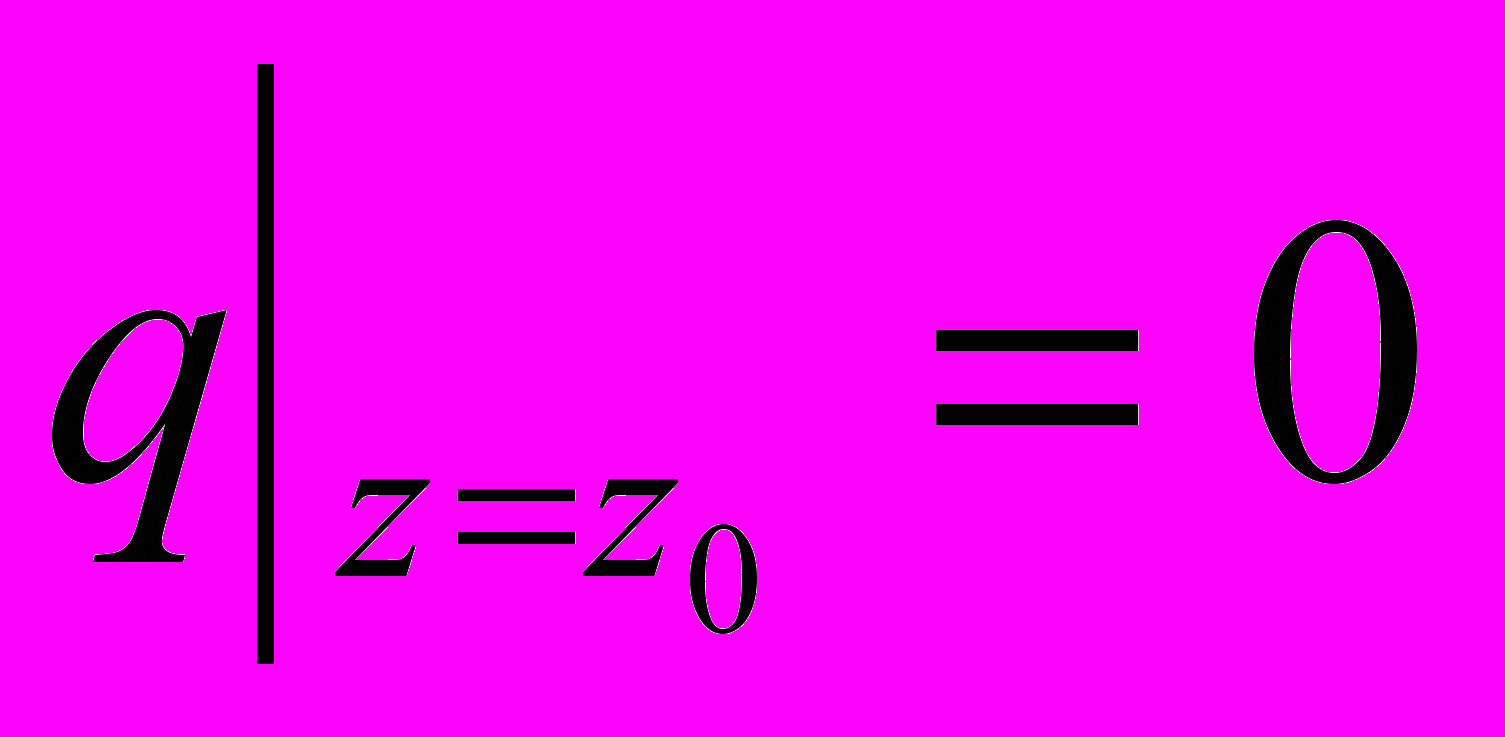Корректность постановки краевых задач для уравнений типа (1) доказана при определенных ограничениях, накладываемых на коэффициенты диффузии и конвекции и для некоторых комбинаций краевых условий в [3].

Естественно, что наиболее адекватно рассматриваемые процессы описывают трехмерные краевые задачи. Очевидны и трудности, сопровождающие реализацию таких математических моделей. К ним относятся: выбор метода решения и корректности соответствующей разностной задачи (при применении разностных методов решения), обеспечение практической вычислительной устойчивости алгоритма, необходимость работы с большими массивами данных. Многие исследователи пытаются решить эти проблемы путем упрощения модели, чаще всего за счет уменьшения размерности задачи.

В данной работе рассмотрим математическую модель, которая может быть представлена трехмерной краевой задачей об эволюции наземного поля примесей Q(x,y,t) и поля примесей приземном слое атмосферы q(x,y,z,t) [2]. Эта задача описывается уравнением (1) при 0, f(x,y,z,t)0 при заданной начальной концентрации полей примеси (2), (8) и краевых условиях (3), (4), (6). Последнее краевое условие дополняется соотношением (7). С учетом последнего соотношения задача о переносе примеси при наличии ветрового подъема и сухого осаждения является существенно нестационарной, причем динамическое равновесие между концентрациями примеси на поверхности и в приповерхностном слое возникает через довольно продолжительное время (t0  -1), поскольку , согласно [4], достаточно малое число.

С учетом (7) перепишем краевое условие (6) в виде:



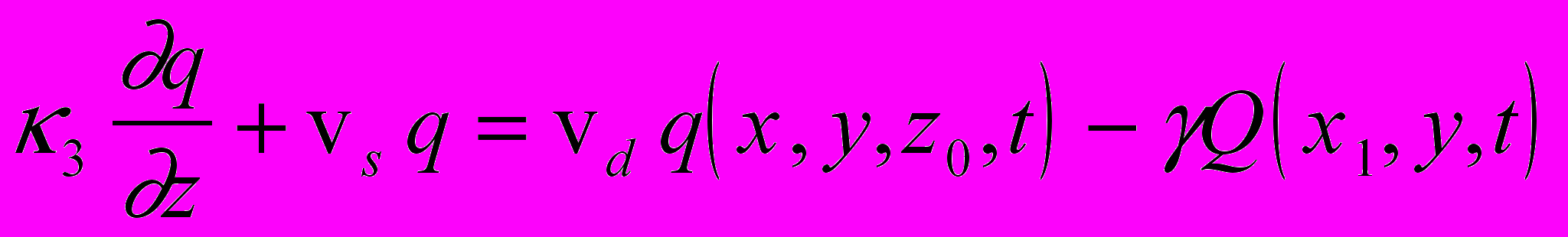
или

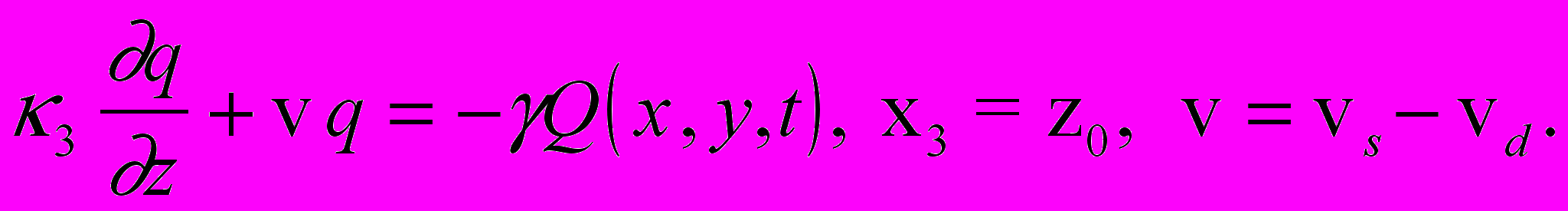(9)

Обозначив 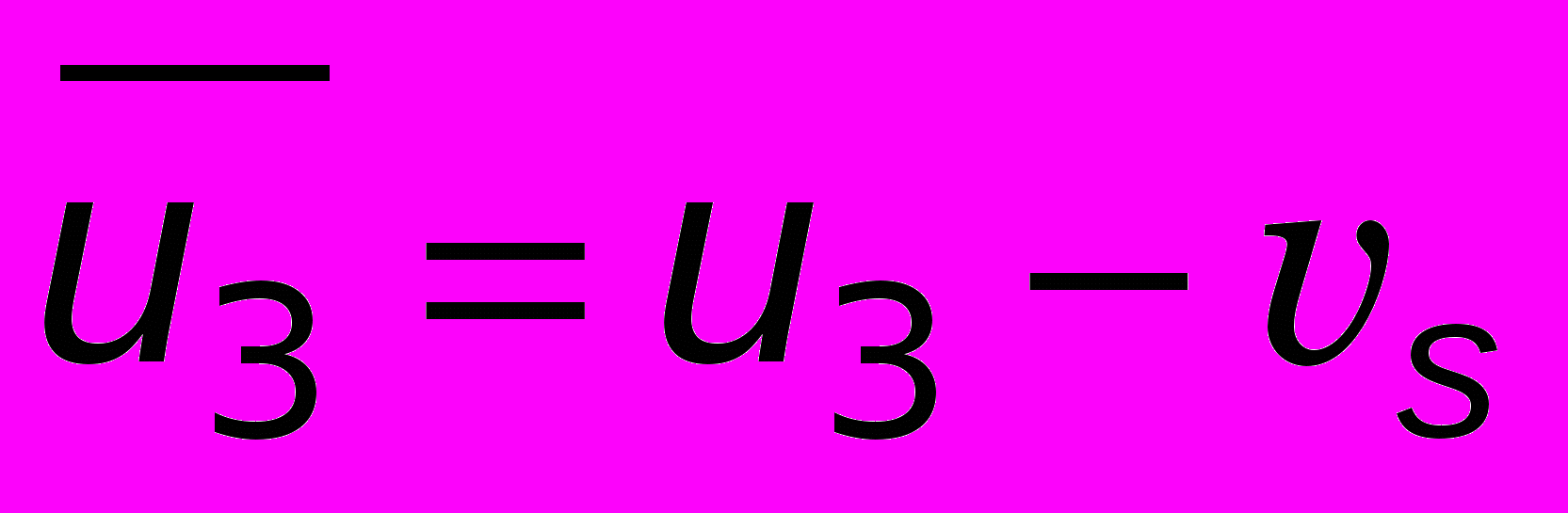, перепишем уравнение (1) в развернутом виде:

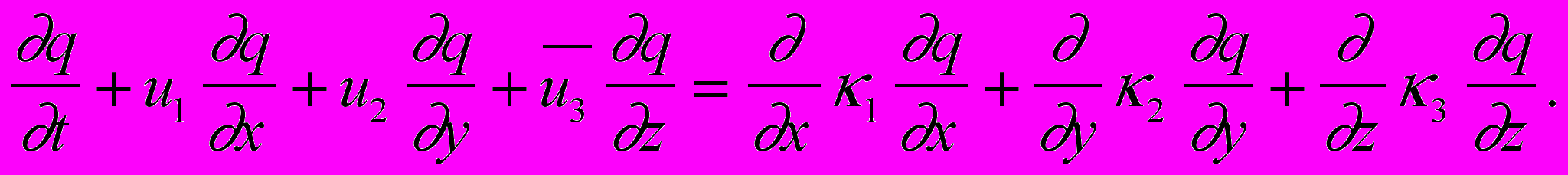(10)

Таким образом, за основу математической модели выбрано уравнение (10) с условиями (2) – (4), (8), (9). При построении численного алгоритма для решения задачи (10), (2) – (4), (8), (9) был использовать разностный метод, предложенный в [4] и была построена разностная схема, которая является монотонной, то есть для нее выполняется сеточный аналог принципа максимума без ограничений на шаги сетки по пространственным переменным.Одной из особенностей рассмотренной задачи явля­ется отсутствие модельных примеров, позволяющих убе­диться в правильности работы вычислительного алгоритма. В качестве одной из схем проверки можно предложить следующее. Предположим, что перенос примеси вдоль одной из координатных осей, например, вдоль оси OY отсутствует, то есть 20, u20. Тогда наша задача вырождается в двумерную, для решения которой разработаны и апробированы надежные алгоритмы. Проводя расчеты по этим алгоритмам и по предложенному алгоритму расчета трехмерной задачи и сравнивая результаты, при их совпадении с необходимой точностью можно считать пред­ложенный алгоритм приемлемым.

Программная реализация описанного алгоритма была осуществлена на языке PASCAL и позволяет даже на ЭВМ типа Pentium с объемом оперативной памяти 32Мб в защищенном режиме решать задачи на сетке размером до 700 000 узлов. Алгоритм решения позволяет за короткое время получать результаты численного моделирования. При этом время счета зависит как от временного промежутка, на протяжении которого моделируются процессы, так и от мощности компьютера.

Проведено численное моделирование для большого количества вариантов при различных начальных и граничных условий, а также различных значениях параметров.

В качестве примера рассмотрим область (Рис.1), представляющей собой единичный куб, в начальный момент концентрация примеси нулевая, кроме точки (0.136, 0.26, 0.05), где концентрация равна 100.

Подстилающая поверхность в начальный момент времени также чиста. Значения остальных физических параметров: 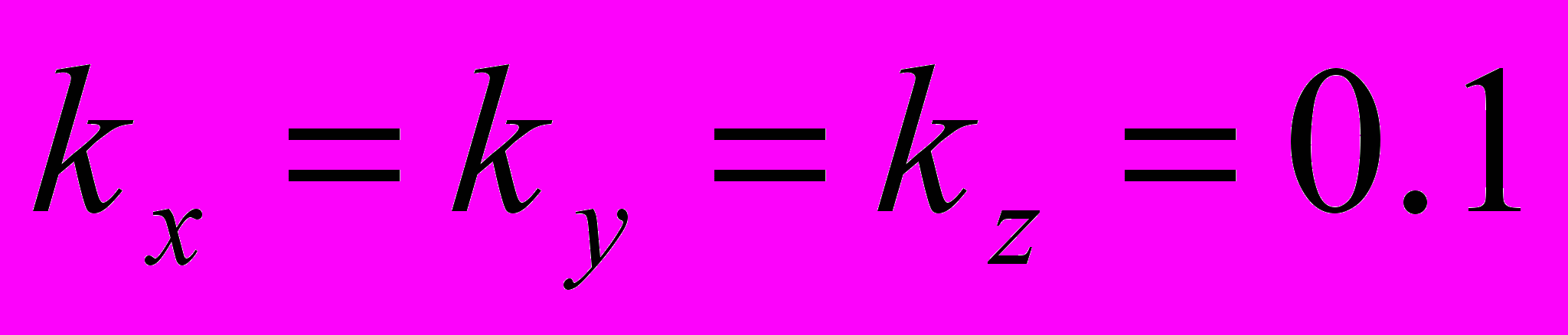; vs =0.4 vd = 0.3;  = 0.004;  = 0.0; f  0.0; vx = 4.0; vy = 2.0; vz = 0.

Параметры разностной схемы: hx = hy = hz = 0.026;  = 1/60;  = 1.0.



Рис.1.



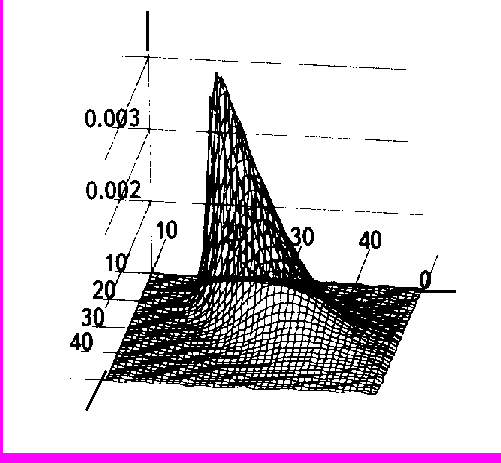
Рис. 2

После проведенных многочисленных численных экспериментов, можно говорить о том, что предложенная математическая модель, а также алгоритм численной реализации позволяют эффективно моделировать процессы распространения примесей, и в том числе на средние расстояния.




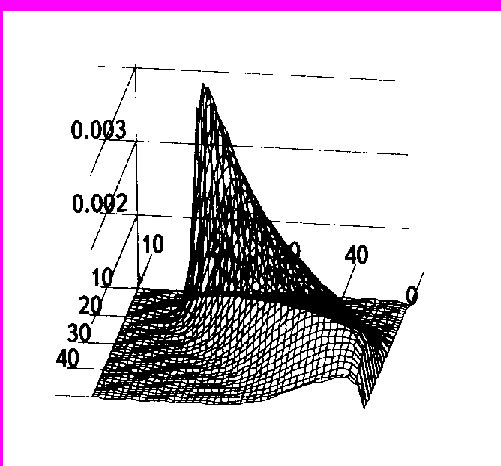
Рис.3



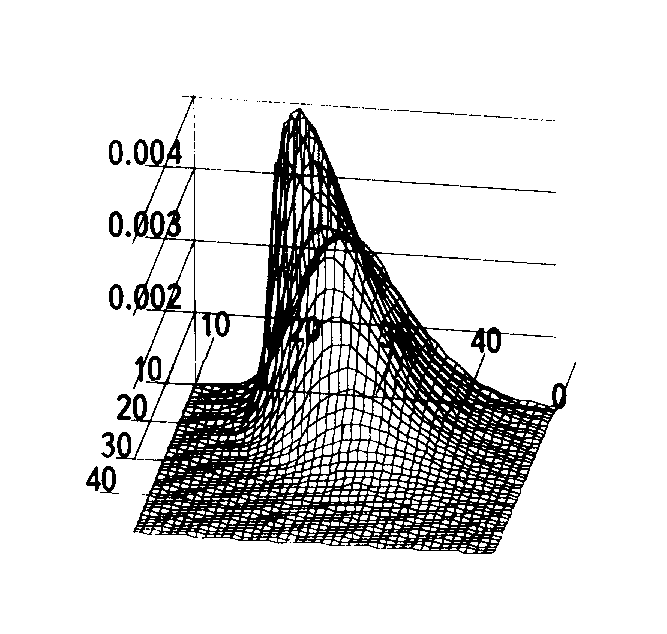
Рис. 4

Таким образом, компьютерное моделирование, базирующееся на предложенной математической модели, позволяет получать информацию о распределении примеси в приземном слое атмосферы от источников загрязнения. При этом можно получить информацию как на будущее, при определенных начальных данных, так и прошлом.

Используемые средства графической визуализации позволяют следить за распространением примесей в процессе численного эксперимента, что актуально как при оценке экстремальных ситуаций, так и при долгосрочном прогнозировании состояния окружающей среды.

При рассмотрении систем эколого-гигиенической безопасности возможность появления информации не только о распространении загрязнений, но и количественная оценка оседания частиц в том или ином месте, позволит более качественно оценивать вредные воздействия, не только на человека, но и среду обитания.

Summary


Revealing of tendencies of environmental contamination, both at the certain moment of time, and for the period of time, from sources of pollution of a ground layer of an atmosphere represents significant interest at the decision of the various problems concerning ecological and hygienic safety.

Modelling with use of the computer allows to receive the information not only for forecasting distribution of pollution, but also about quantity of pollution which appeared in the certain territory for the period of time. The spread of contaminant in the atmosphere and on the earth surface due to wind transfer and diffusion is simulated with a monotonous finite-difference scheme for 3D diffusion equation. The SOR method is used for solving the problem.