Geum.ru

Порівняльний аналіз динаміки виробництва сталі у регіонах світу завдання

Вид материалаРеферат

Содержание


4. Кореляційний аналіз
Південна Корея
Список використаної літератури
Подобный материал:
1   2   3

4. КОРЕЛЯЦІЙНИЙ АНАЛІЗ


Кореляція - це статистична залежність між випадковими величинами, що не має строго функціонального характеру, при якій зміна математичного очікування однієї випадкової величини приводить до зміни математичного очікування іншої випадкової величини.

Застосування методології кореляційного аналізу пред'являє до вихідної інформації певні вимоги:
  • статистична вибірка об'єктів повинна бути однорідною або, інакше кажучи, розглянуті об'єкти повинні бути однотипними;
  • статистична вибірка об'єктів повинна бути досить численною (вимога достатності числа спостережень);
  • досліджувані показники повинні бути обмірювані з однаковою точністю;
  • факторні ознаки, що включають у дослідження, повинні бути незалежні один від одного, тому що наявність тісного зв'язку між ними свідчить про те, що вони характеризують одні і ті ж самі сторони досліджуваного явища й значною мірою дублюють один одного; повністю виключаються фактори, функціонально пов'язані з результуючою ознакою.

Методологія кореляції (у вузькому змісті) застосовується при вимірі за допомогою певних статистичних показників (коефіцієнтів кореляції), ступеня зв'язаності або міри залежності двох або більше ознак.

За допомогою кореляційного аналізу оцінюється сила стохастичного зв'язку, а за допомогою регресійного аналізу - форма цього зв'язку.

Тіснота зв'язку між двома ознаками виміряється рядом показників, найбільш важливим і застосовуваним з яких при лінійній формі зв'язку є коефіцієнт кореляції, оцінка якого за вибірковим даними визначається по формулі:


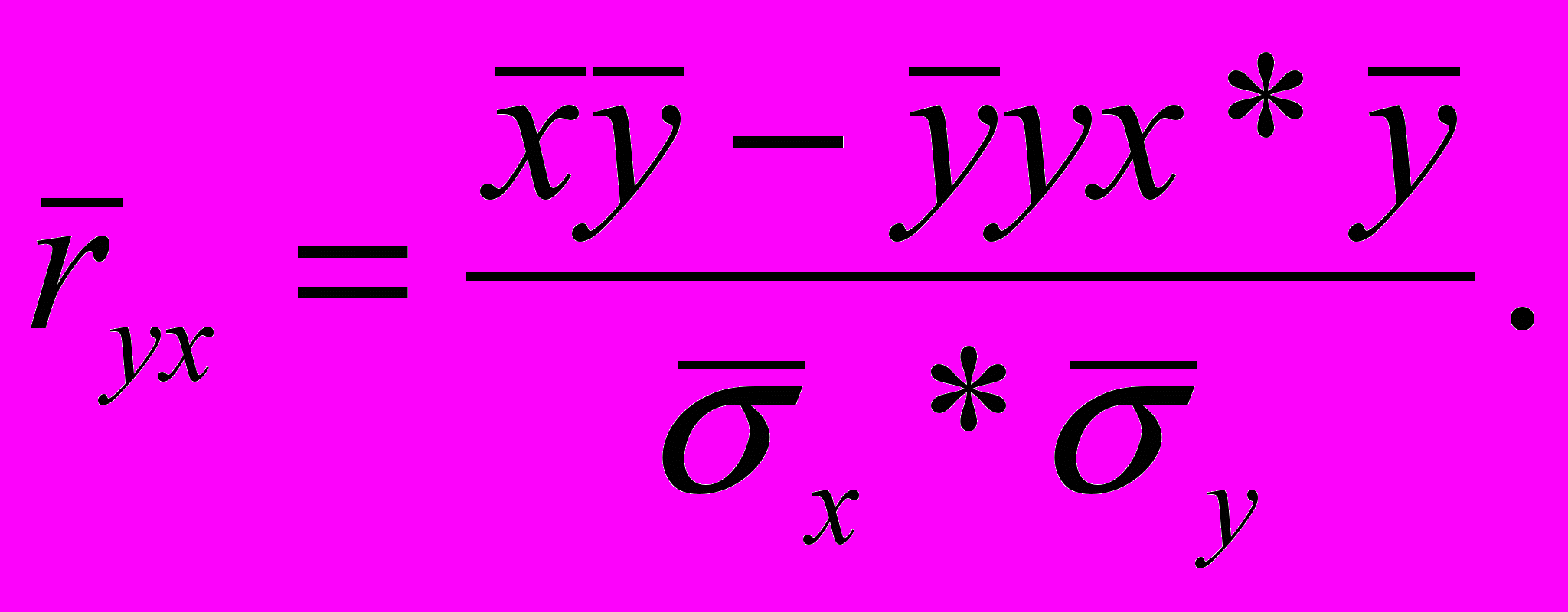(4.1.)

де:




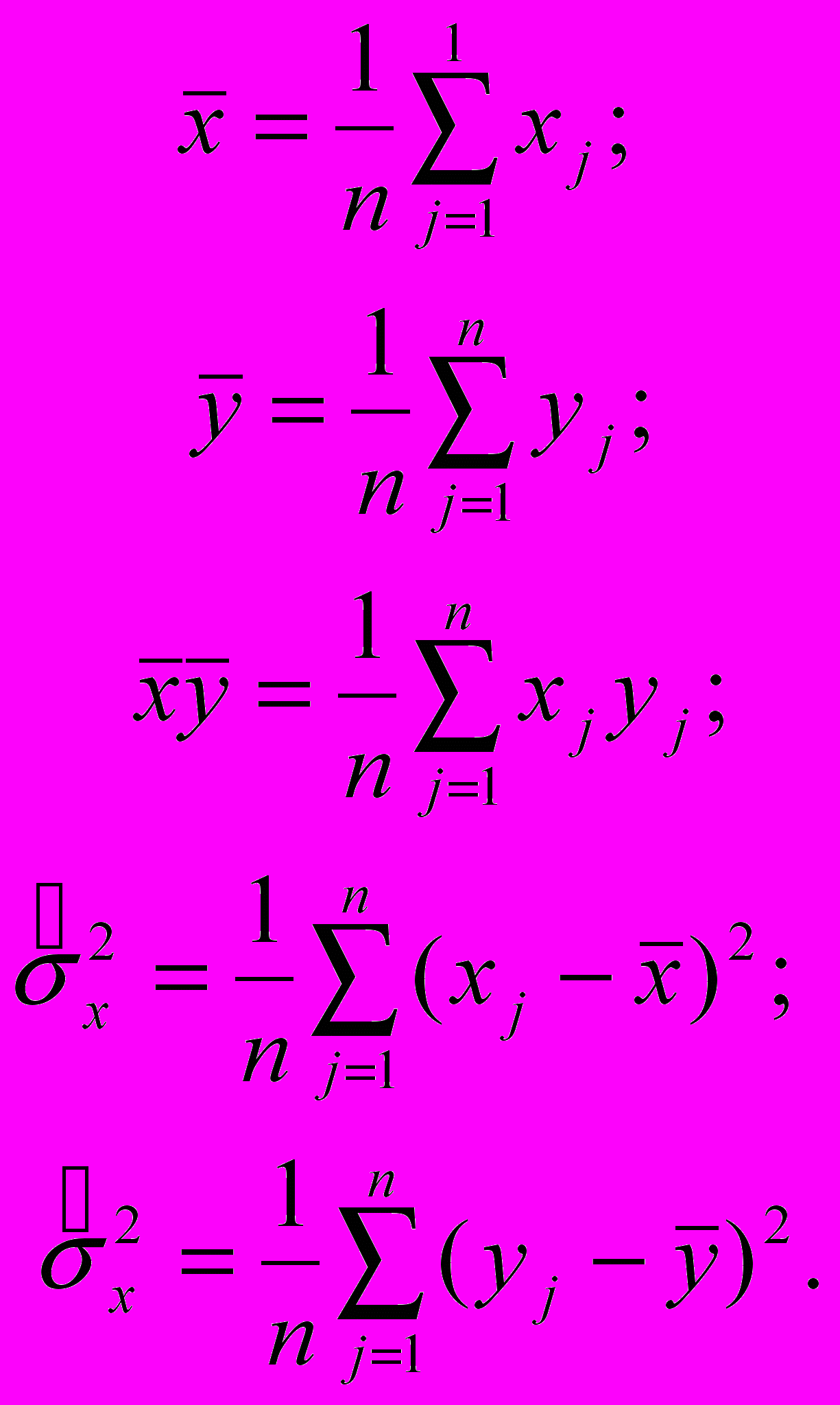
Коефіцієнт кореляції є безрозмірною величиною; його величина не залежить від вибору одиниць виміру обох ознак. Коефіцієнт кореляції приймає значення від -1 до 0, якщо зв'язок зворотній, і від 0 до +1, якщо зв'язок прямий. Якщо значення коефіцієнта по абсолютній величині дорівнює близько одиниці, то між ознаками існує тісний лінійний зв'язок; якщо - близько до 0, те це свідчить про відсутність лінійного зв'язку між ознаками, але не про відсутність зв'язку між ними взагалі.

Досить проблематично зробити обґрунтований висновок про наявність лінійного зв'язку, якщо коефіцієнт кореляції приймає невеликі значення 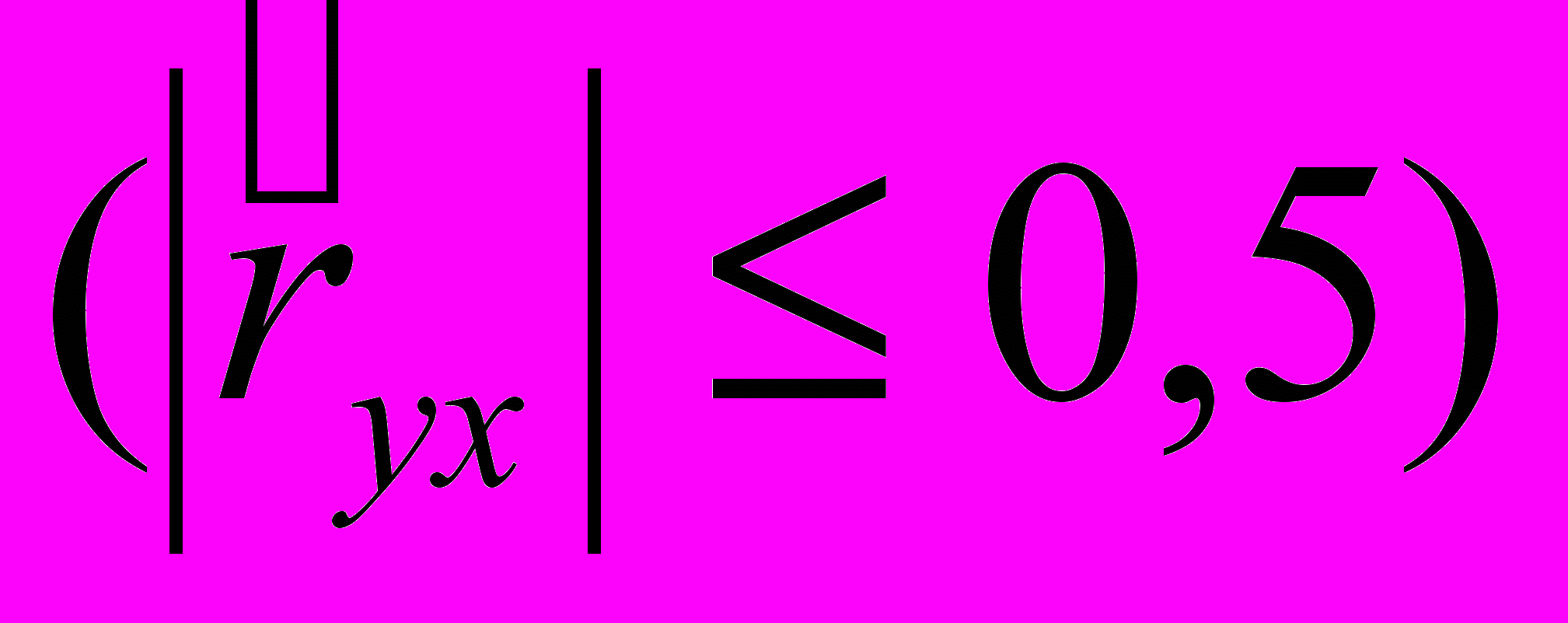. У таких випадках можна провести перевірку гіпотези про значимість зв'язку, який ґрунтується на розподілах вибіркових кореляційних характеристик.

Якщо розподіл випадкових величин 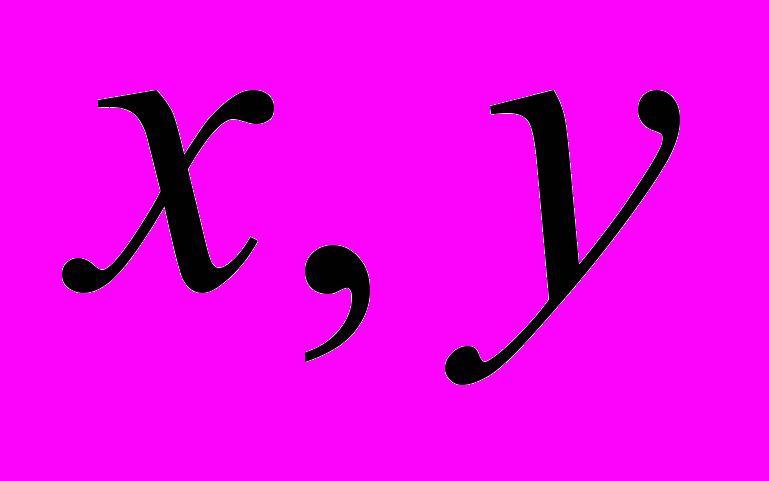– нормальний, то вибірковий коефіцієнт кореляції значимості відрізняється від нуля, повинна виконуватись умова:


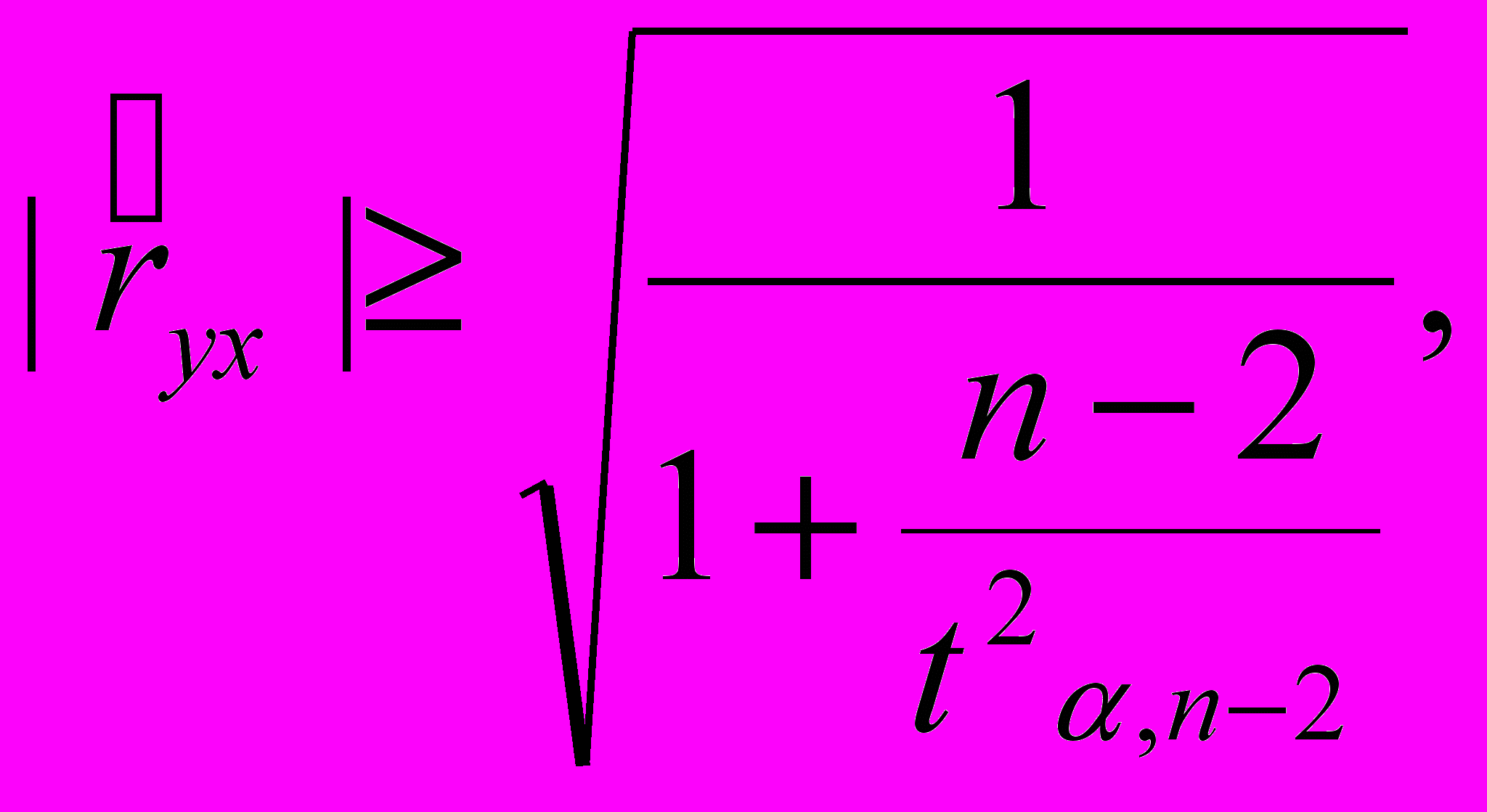(4.2)

де:

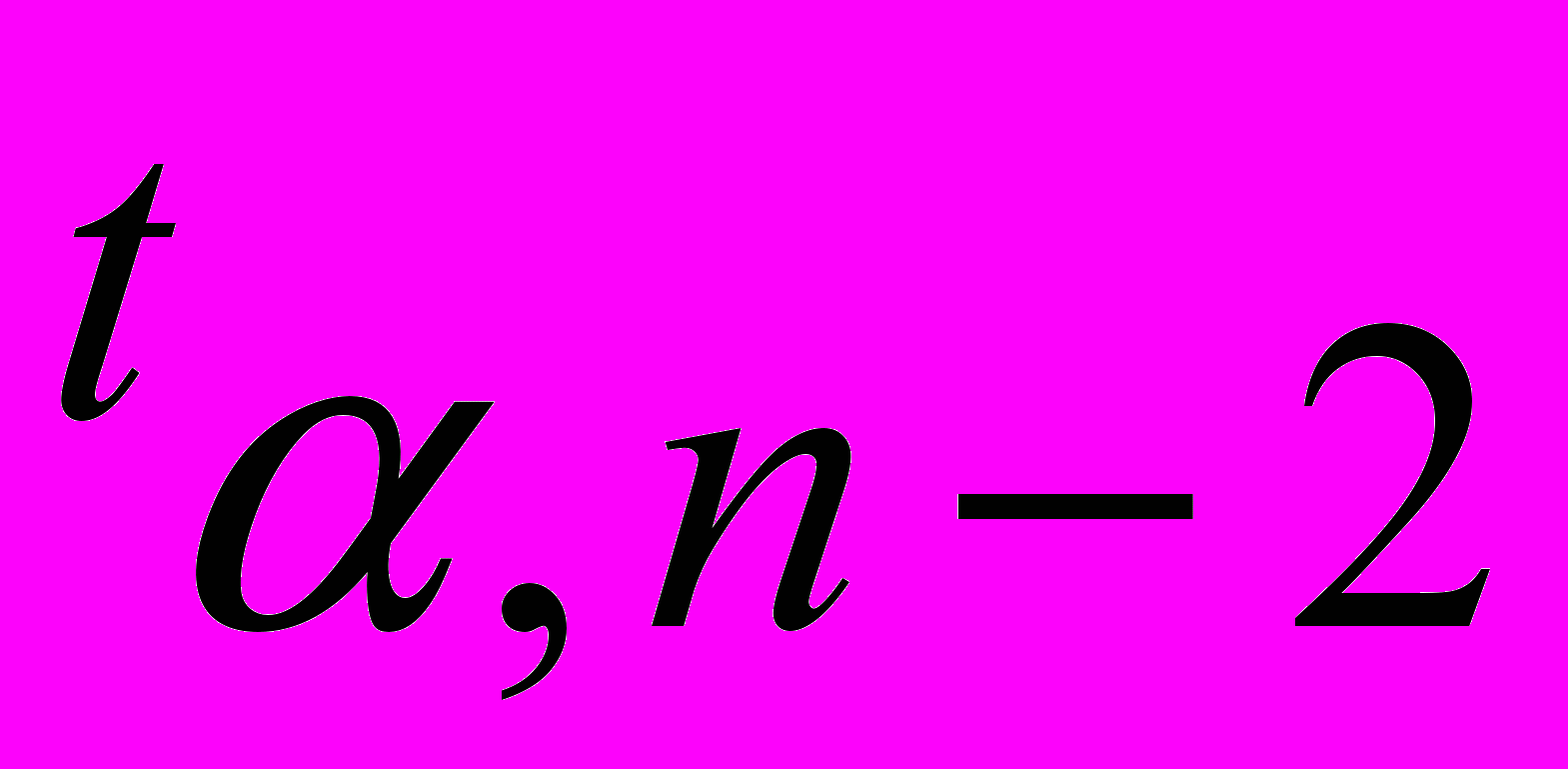– критичне значення розподілу Стьюдента з (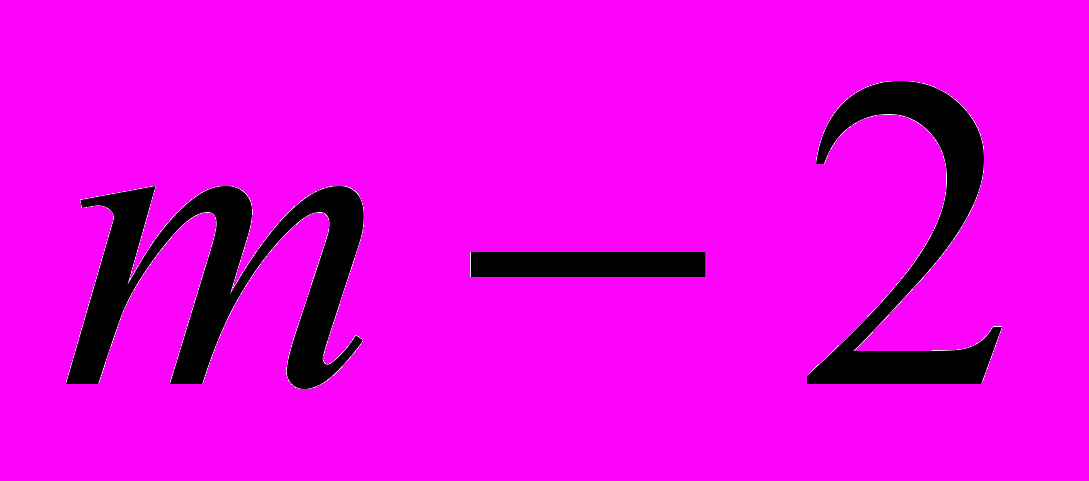) ступенями свободи, що відповідає рівню значимості .

Перевірка статистичної значимості коефіцієнта кореляції може здатися досить трудомісткою процедурою, особливо для тих, хто тільки починає використати статистичні методи.

Важливим моментом перевірки статистичної значимості коефіцієнта кореляції є той факт, що коефіцієнт кореляції досить точно оцінює ступінь тісноти зв'язку лише у випадку наявності лінійної залежності між ознаками. При наявності ж криволінійної залежності коефіцієнт кореляції зменшує ступінь тісноти зв'язку і навіть може бути дорівнювати нулю, тому в таких випадках необхідно використовувати як показник тісноти зв'язку кореляційне відношення, оцінка якого за вибірковими даними визначається по формулі:


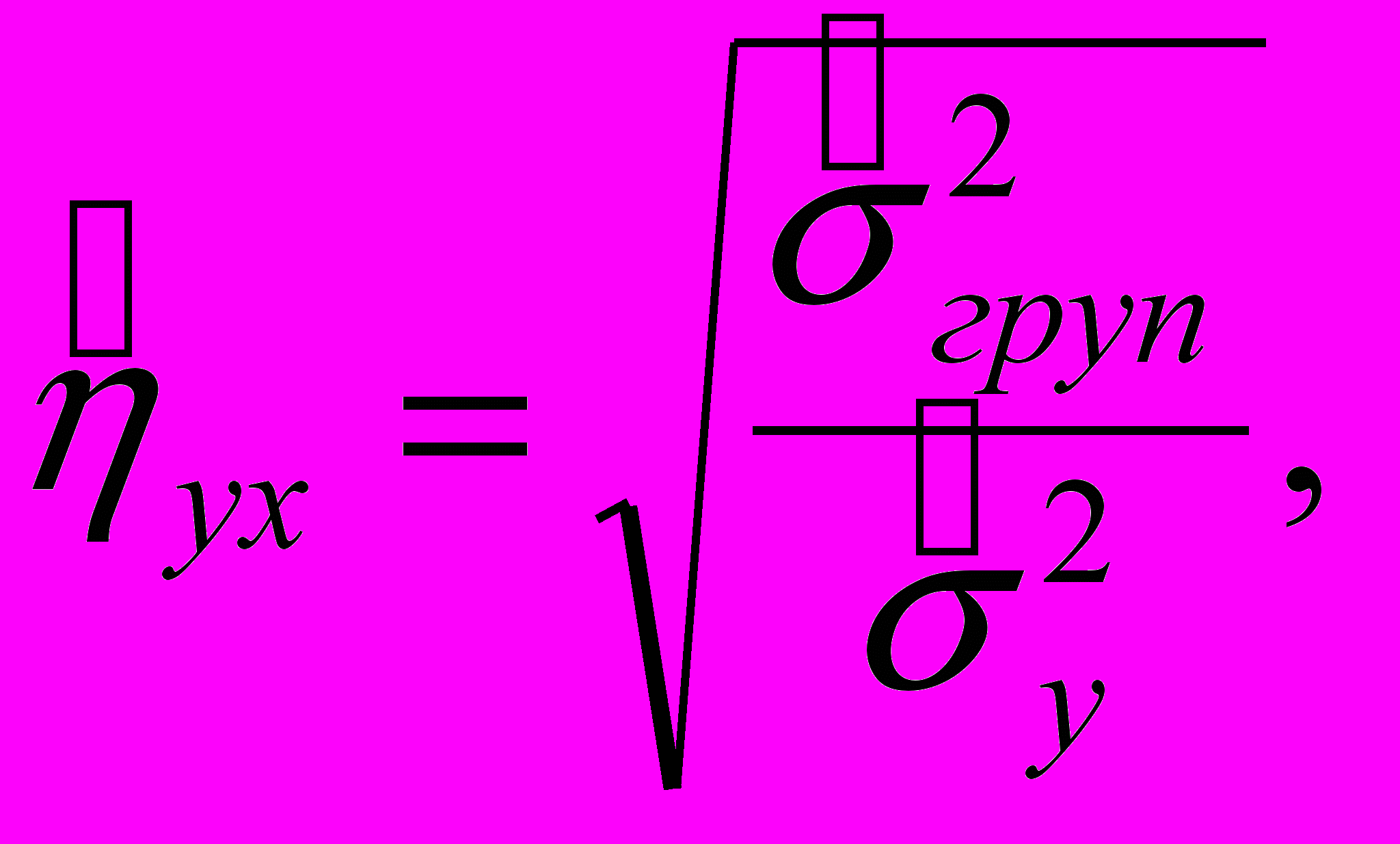(4.3)


де:

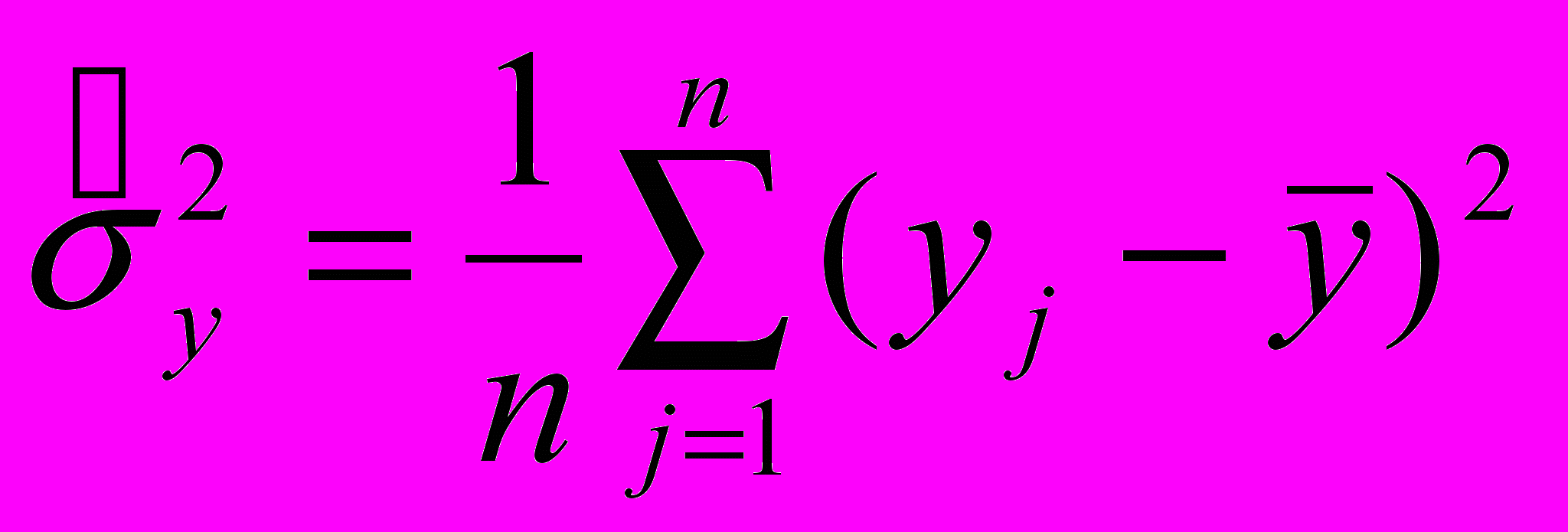– загальна дисперсія результуючої ознаки;

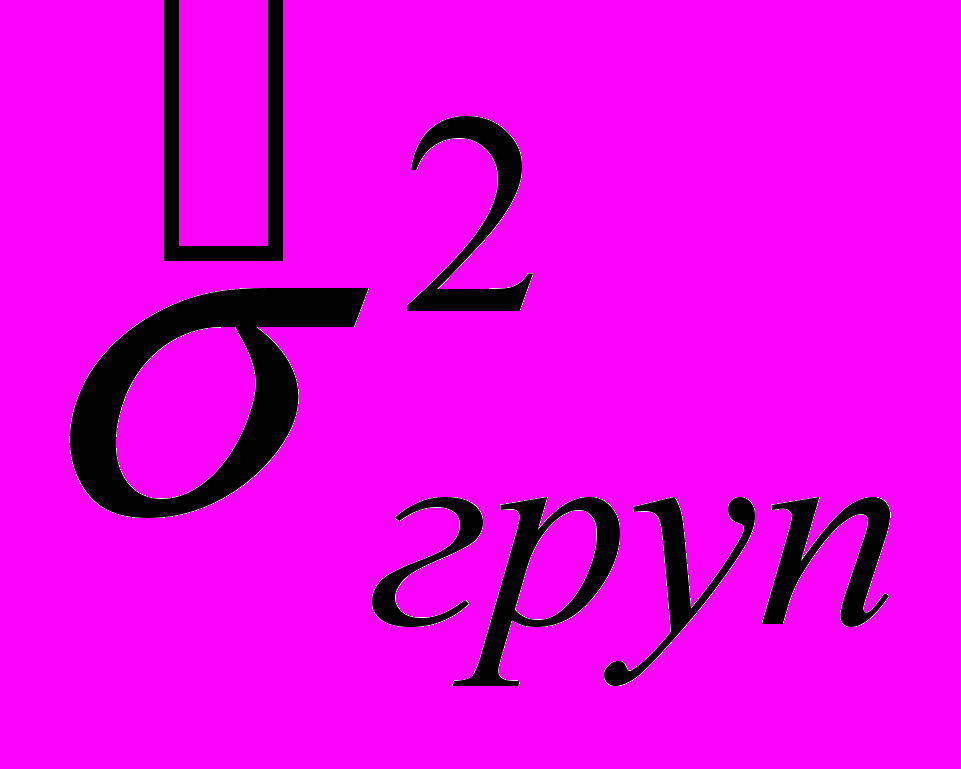– дисперсія групових середніх.

Дисперсія групових середніх характеризує ту частину зміни результуючої ознаки, що складається під впливом зміни ознаки - фактору, покладеного в основу угруповання. Для її визначення використають формулу:


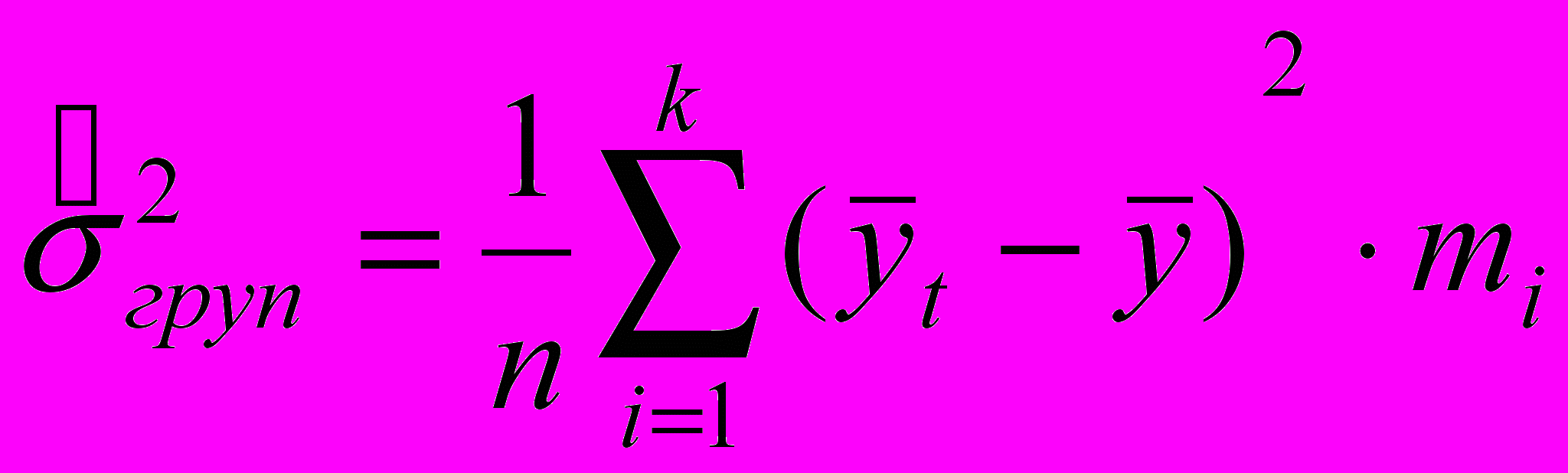, (4.4)


де:

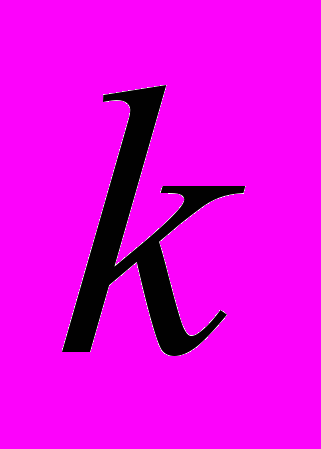– кількість груп;

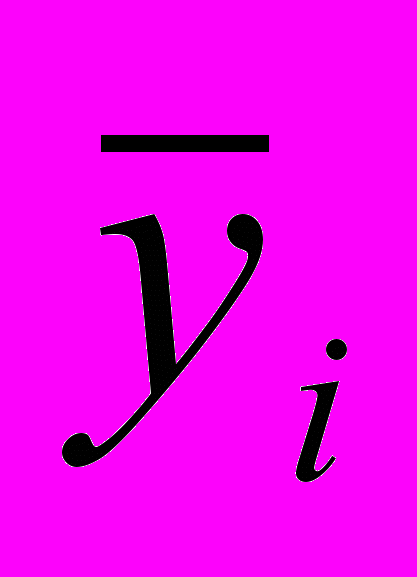– середнє значення результуючої ознаки в i-групі.

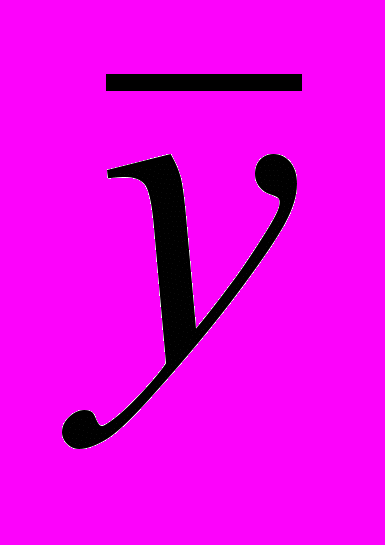– загальне середнє значення результуючої ознаки у вибірці.

Кореляційне відношення змінюється від 0 до 1. Якщо зв'язок відсутній, то кореляційне відношення дорівнює нулю. У цьому випадку дисперсія групових середніх буде дорівнює нулю, тоді всі її групові середні будуть рівні між собою і між групової варіації не буде. Якщо зв'язок функціональний, то кореляційне відношення буде дорівнює одиниці. У цьому випадку дисперсія групових середніх дорівнює загальної дисперсії. Чим більше значення кореляційного відношення наближається до одиниці, тим ближче до функціональної залежність між ознаками.

При перевірці можливості використання лінійної залежності для опису форми зв'язку між досліджуваними факторами використовують наступне правило: визначають різницю квадратів 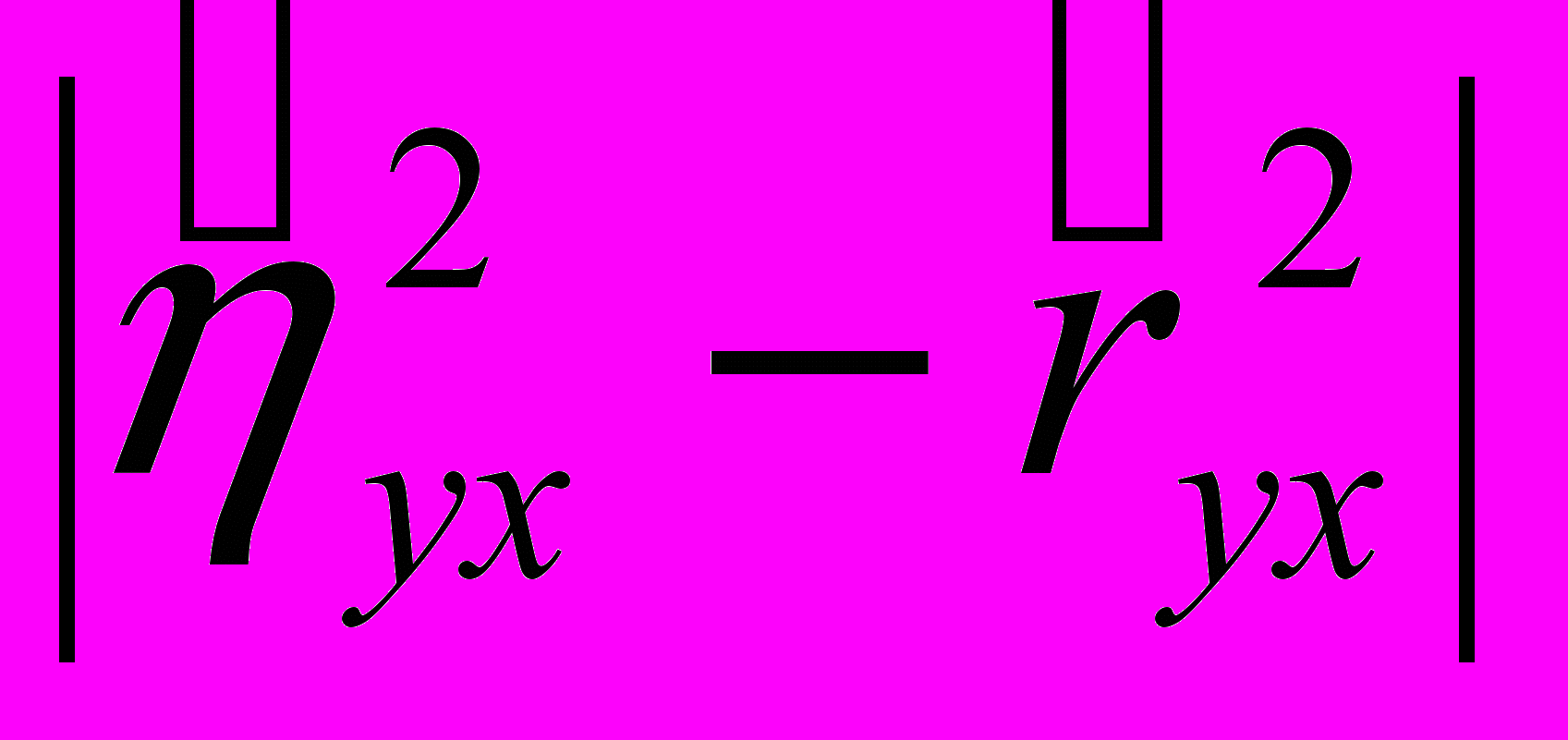, якщо ця різниця менше 0,1; то вважається можливим застосувати лінійне рівняння для опису залежності. Крім цього, існує загальне правило: якщо значення кореляційного відношення перевищує абсолютне значення коефіцієнта кореляції, то є підстава припускати, що між досліджуваними величинами існує нелінійний зв'язок.


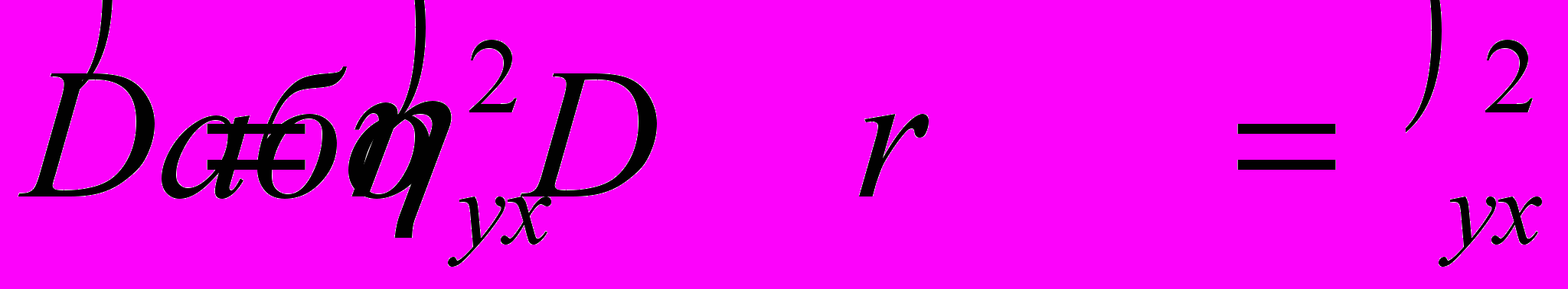. (4.5)


Коефіцієнт детермінації визначає частку загальної варіації результуючої ознаки, що пояснюється зміною ознаки - фактору. Цей показник може приймати значення від 0 до 1.

Матриця коефіцієнтів кореляції динамічних рядів динаміки виробництва сталі в різних країнах представлено в табл. 4.1. Як видно із цієї таблиці, між ринками різних країн існує досить тісний зв’язок. Але між ринками України та США та Росії та США існує зворотній зв'язок .


Табл. 4.1 Матриця кореляції динамічних рядів динаміки виробництва сталі

 
Україна
Росія
Німеччина
Італія
Туреччина
США
Бразилія
Китай
Японія
Південна Корея
Індія

Україна
1
0,96
0,45
0,61
0,62
-0,14
0,68
0,71
0,72
0,42
0,65

Росія
0,96
1
0,45
0,71
0,67
-0,09
0,70
0,76
0,79
0,44
0,71

Німеччина
0,45
0,45
1
0,82
0,76
0,72
0,72
0,75
0,63
0,75
0,78

Італія
0,61
0,71
0,82
1
0,83
0,57
0,71
0,90
0,72
0,73
0,88

Туреччина
0,62
0,67
0,76
0,83
1
0,47
0,94
0,94
0,48
0,96
0,96

США
-0,14
-0,09
0,72
0,57
0,47
1
0,41
0,43
0,30
0,51
0,46

Бразилія
0,68
0,70
0,72
0,71
0,94
0,41
1
0,81
0,45
0,91
0,85

Китай
0,71
0,76
0,75
0,90
0,94
0,43
0,81
1
0,64
0,83
0,98

Японія
0,72
0,79
0,63
0,72
0,48
0,30
0,45
0,64
1
0,32
0,58

Південна Корея
0,42
0,44
0,75
0,73
0,96
0,51
0,91
0,83
0,32
1
0,87

Індія
0,65
0,71
0,78
0,88
0,96
0,46
0,85
0,98
0,58
0,87
1



Висновки


1. Починаючи з 2002 року світове виробництво сталі повільно зростає. Всі розглянуті країни збільшують виробництво сталі. Лідирують Китай, США, Японія, Німеччина, Росія. Серед світових регіонів Азія залишається найбільшим виробником сталі (39 %), на другому місці - Америка, на третьому - Європа.

2. Аналізуючи сучасний стан світового ринку чорних металів, можна відзначити, що існує величезне число незалежних виробників і наявність надлишкових потужностей зараз робить світовий ринок чорних металів практично неконтрольованим. Це призводить до цінових війн, антидемпінгових процесів і циклічних змін зростання і падіння.

3. У 2007 році встановлено історичний рекорд у світовому виробництві стали - 1343,5 млн. т. У порівнянні з 2006 р. цей показник збільшився на 7,5%. Для основних країн – виробників сталі за 12 місяців 2007 р. із процентними змінами в дужках відносно 2006 р.: Україна - 42,83 млн. т (+1,93%); Росія - 72,22 млн. т. (+1,39%); Германія - 48,55 млн. т. (+1,33%); Італія - 37,99 млн. т. (+0,37%); Туреччина - 25,76 млн. т. (+2,45%); США - 98,18 млн. т. (-0,38%); Бразилія - 33,78 млн. т. (+2,88%); Китай - 489,241 млн. т. (+66,58%); Японія - 120,196 млн. т. (+3,97%); Південна Корея - 51,367 млн. т. (+2,91%); Індія - 53,08 млн. т. (+3,63%);

4. Українська чавуноливарна та сталеливарна галузь міцно зав'язані на експорті, а тому на їх розвиток справляють значний вплив тенденції на світовому ринку. Серед основних ризиків діяльності металургійної галузі – несприятлива кон`юнктура на світових ринках, зменшення попиту на метали.

5. Вітчизняна чорна металургія має низьку конкурентоспроможність на зовнішніх ринках і недостатній інноваційний потенціал галузі.


СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

1. steel.org

2. “Годовой обор развития металлургической отрасли в Украине” //Бизнес, 2002, № 34, с.32-25.

3. Сергей Кукин. Долгое прощание с мартеном // Эксперт, 2007. №28. С. 58 – 63.

4. “Світовий ринок чорних металів: сучасний стан та перспективи розвитку” // “Метал України”, 2007, № 25, с.11-17

5. Буркинський Б. Інноваційний рівень виробництва та конкурентоспроможність чорної металургії України // v.ua/file/link/78897/file/Burkinski_4_06_U.pdf

6. ссылка скрыта

7. torg.ru/

8. Брантд З. Анализ данных: статистические и вычислительные методы для научных работников и инженеров. – М.: Мир, АСТ, 2003. – 686 с.