Geum.ru

Графічне інтегрування

Вид материалаДокументы

Содержание


Зразок виконання завдання.
Завдання для самостійної роботи
Подобный материал:
Графічне інтегрування


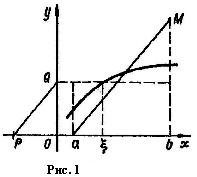
Наближене обчислення інтеграла методом графічного інтегрування застосовується тоді, коли підінтегральна функція задана графічно. Нехай на [a; b] задана неперервна крива, рівняння якої y=f(x). На підставі теореми про середнє значення для певного інтеграла існує така точка ξ [a; b], що 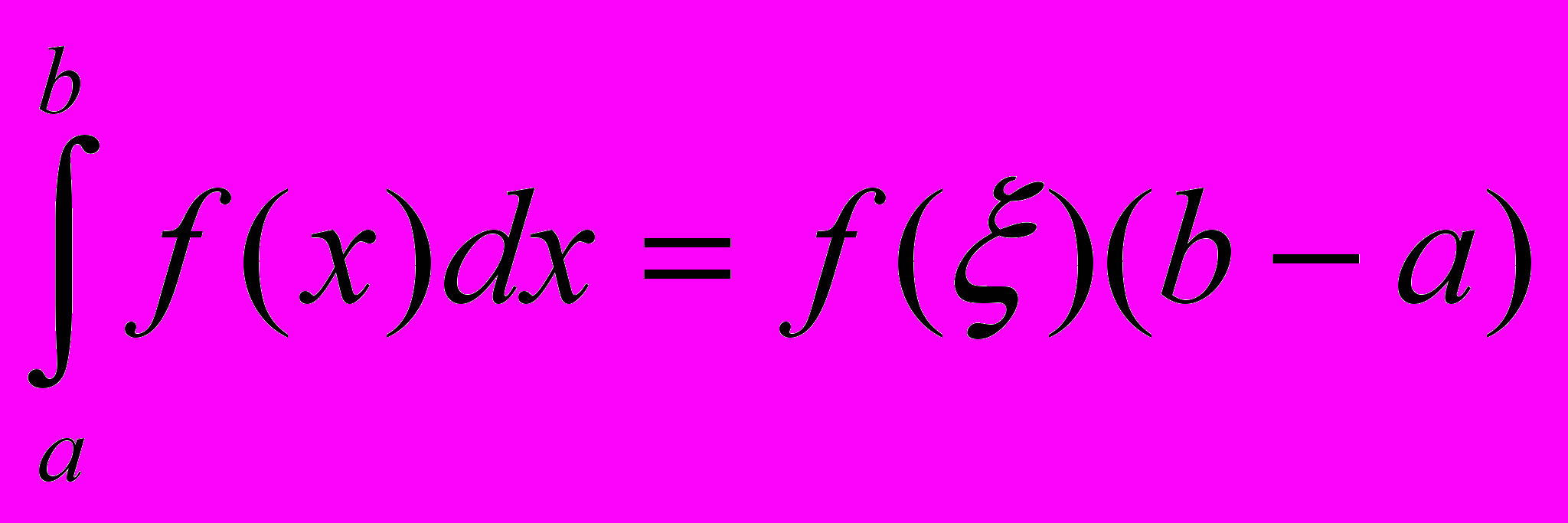. Геометрично це означає, що площа криволінійної трапеції чисельно дорівнює площі прямокутника з основою [a; b] і висотою f(ξ). Розглянемо криволінійну трапецію (рис. 1) і проведемо горизонтальну пряму приблизно так, щоб одержати необхідний прямокутник. Абсцисами точок перетину прямої і кривої будуть ті точки ξ, про які згадується в теоремі про середнє значення. Відкладемо на осі Ох ліворуч від початку координат одиничний відрізок ОР і продовжимо проведену горизонтальну пряму до перетину віссю ординат (якщо а<0, то краще спочатку ліворуч від а провести вертикальну пряму й при подальших діях замінити вісь Oy цією прямою). Нехай пряма перетне вісь Oy у точці Q, тоді OQ= f(ξ). З'єднаємо точки Р и Q і із точки а проведемо пряму аМ, паралельну РQ, до перетинання в точці М з вертикаллю, проведеної із точки b. Покажемо, що b= 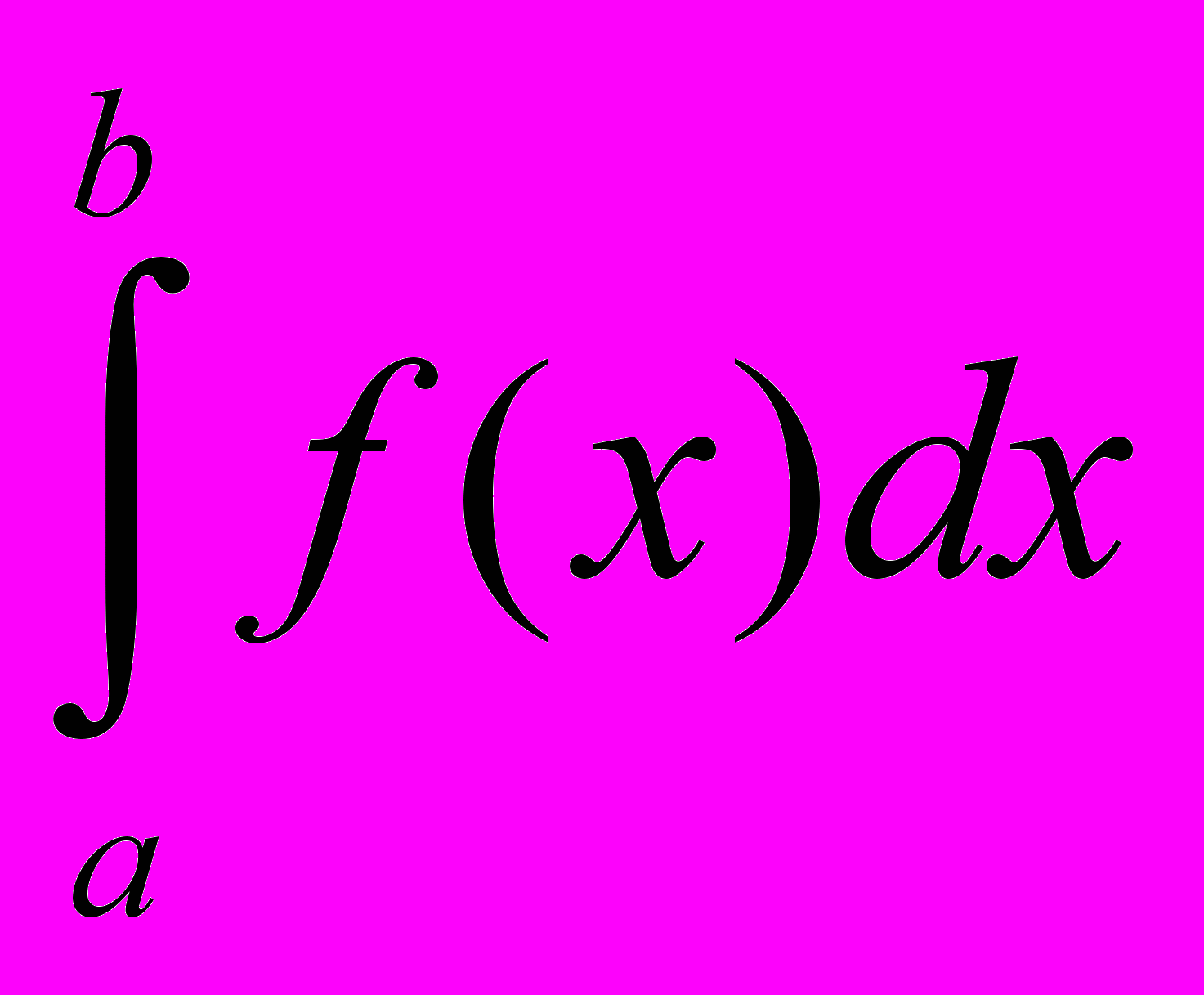, тобто величина побудованого відрізка чисельно дорівнює значенню певного інтеграла. Дійсно, ∆ PQO ~ ∆ aMb. Звідси

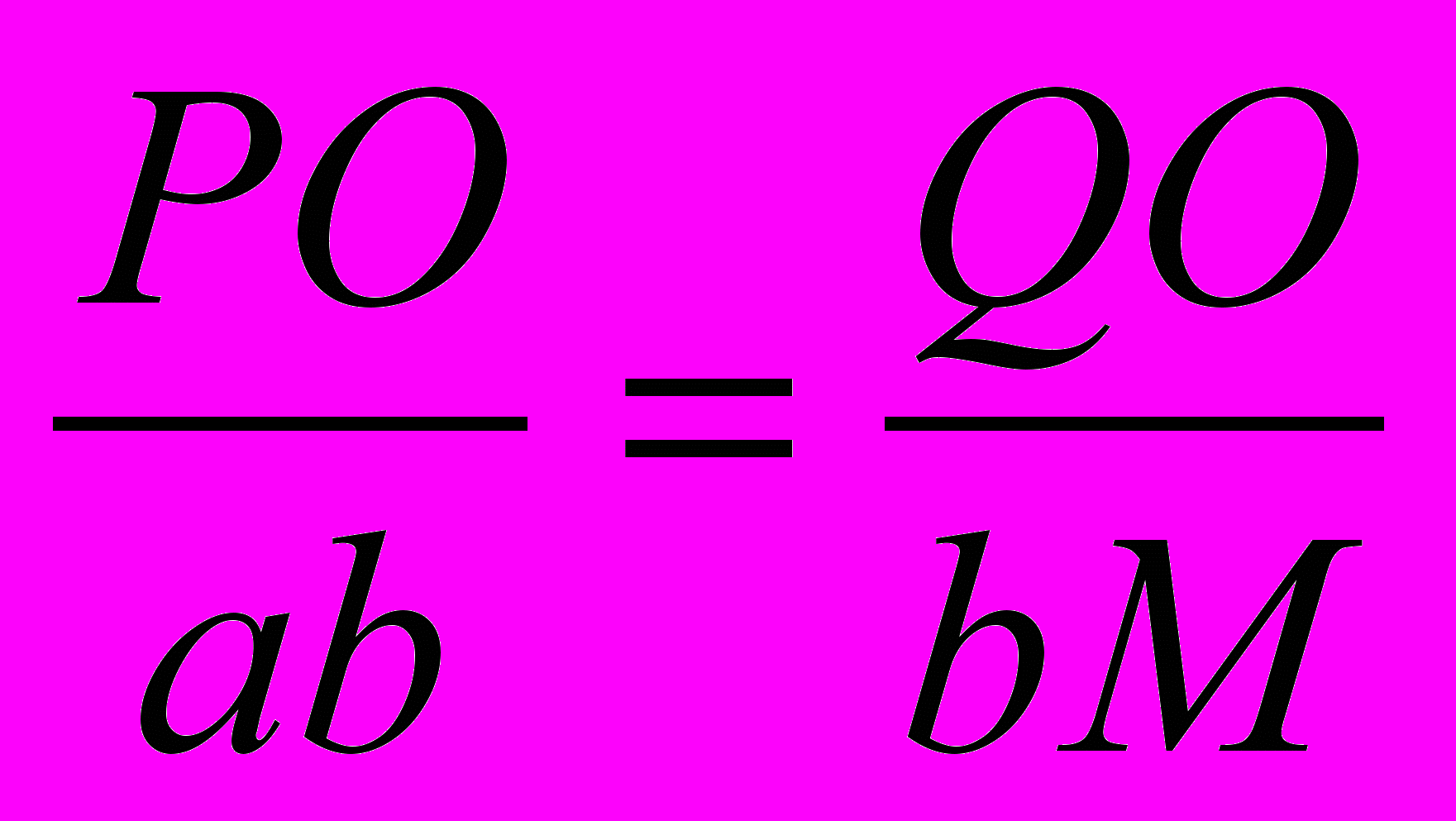, bM=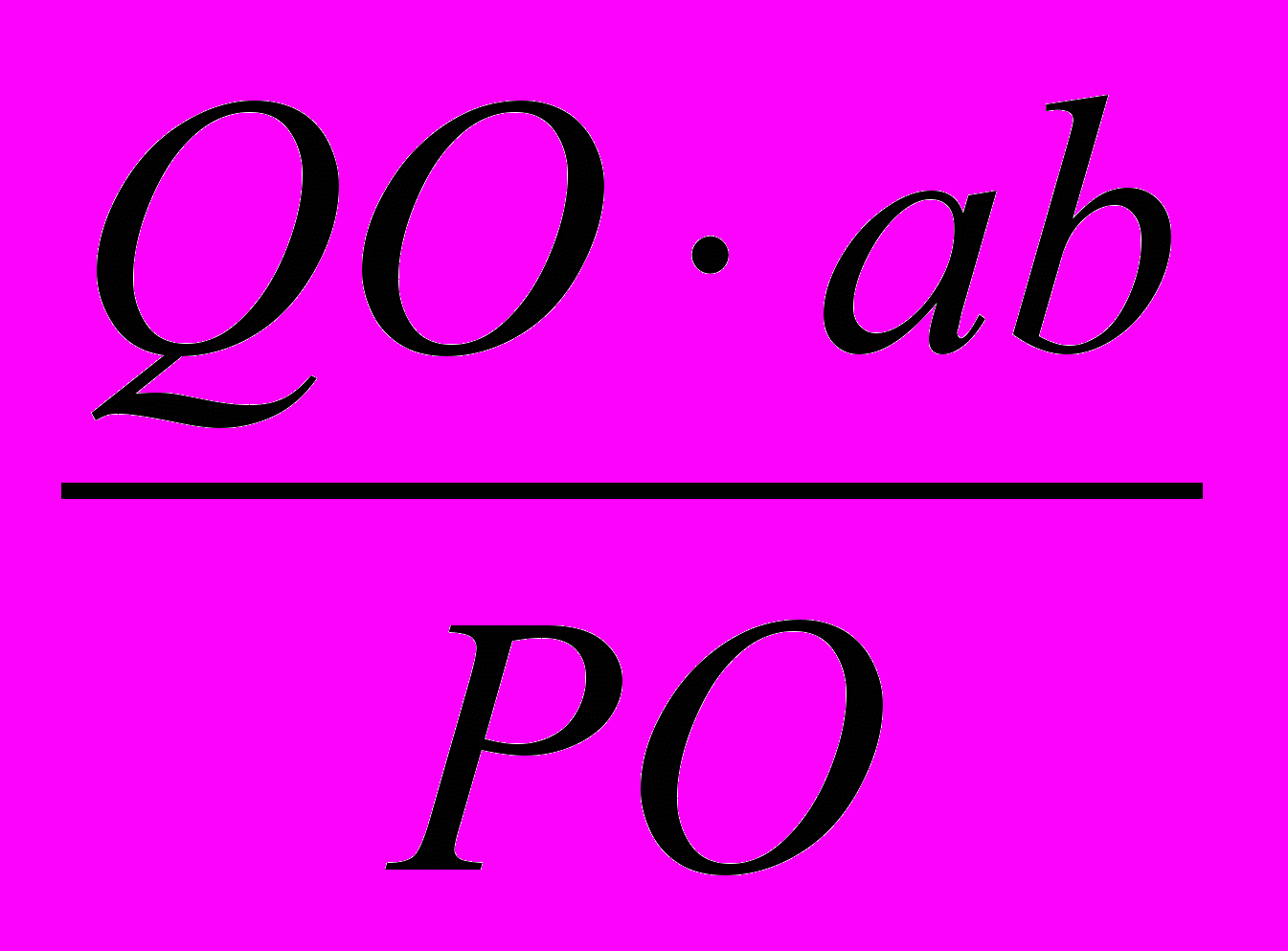= f(ξ)(b - a)= .

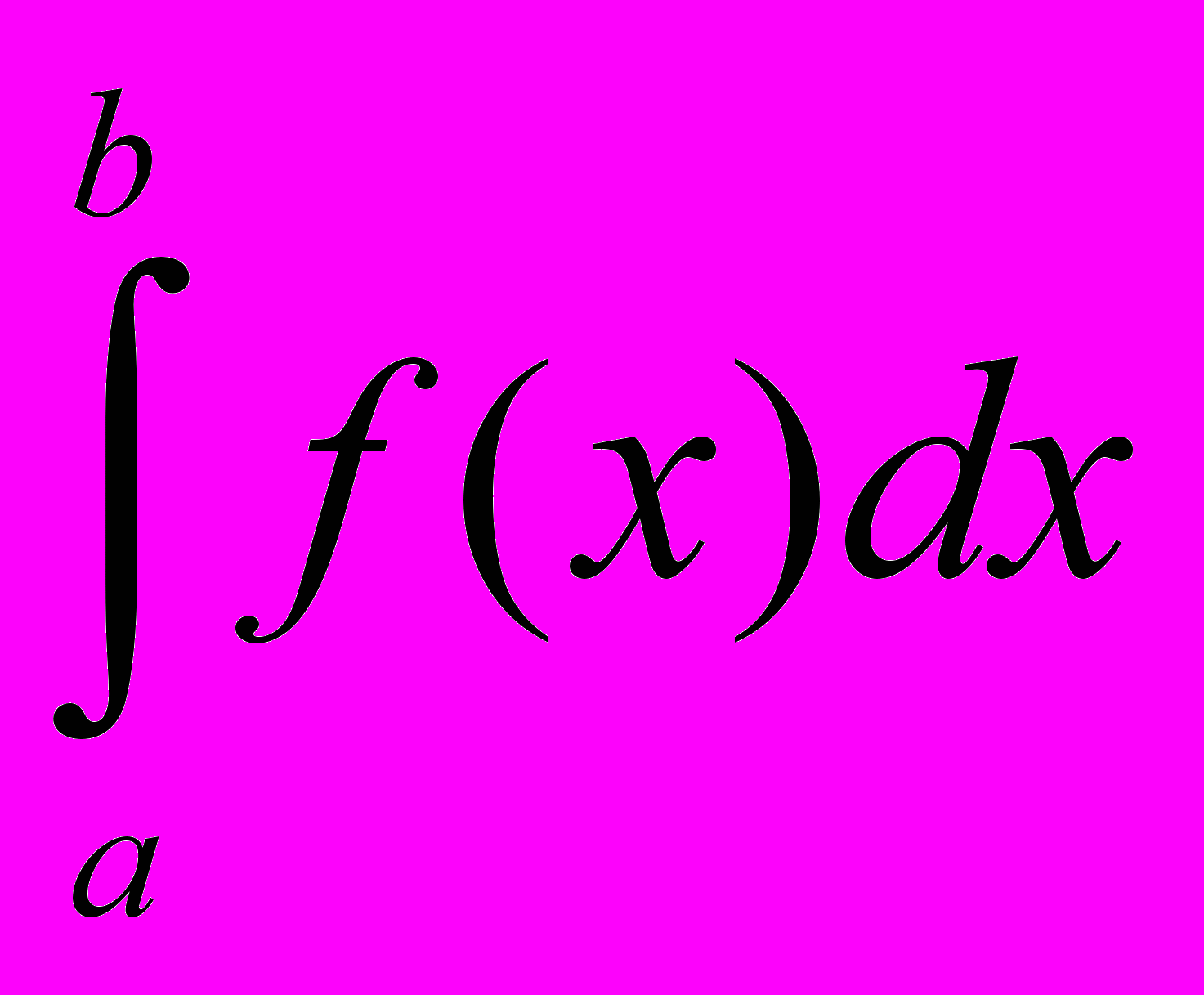З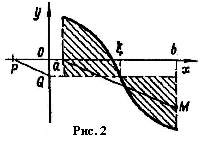ауваження. На рис. 1 функція f(x)>0. Однак отриманий результат має місце для будь-якої неперервної на [a; b] функції y=f(x). Наприклад, на рис. 2 функція f(x) міняє знак на [a; b]. Заштриховані площі приблизно рівні. Оскільки площа частини криволінійної трапеції, розташованої нижче осі Ох, більша, то 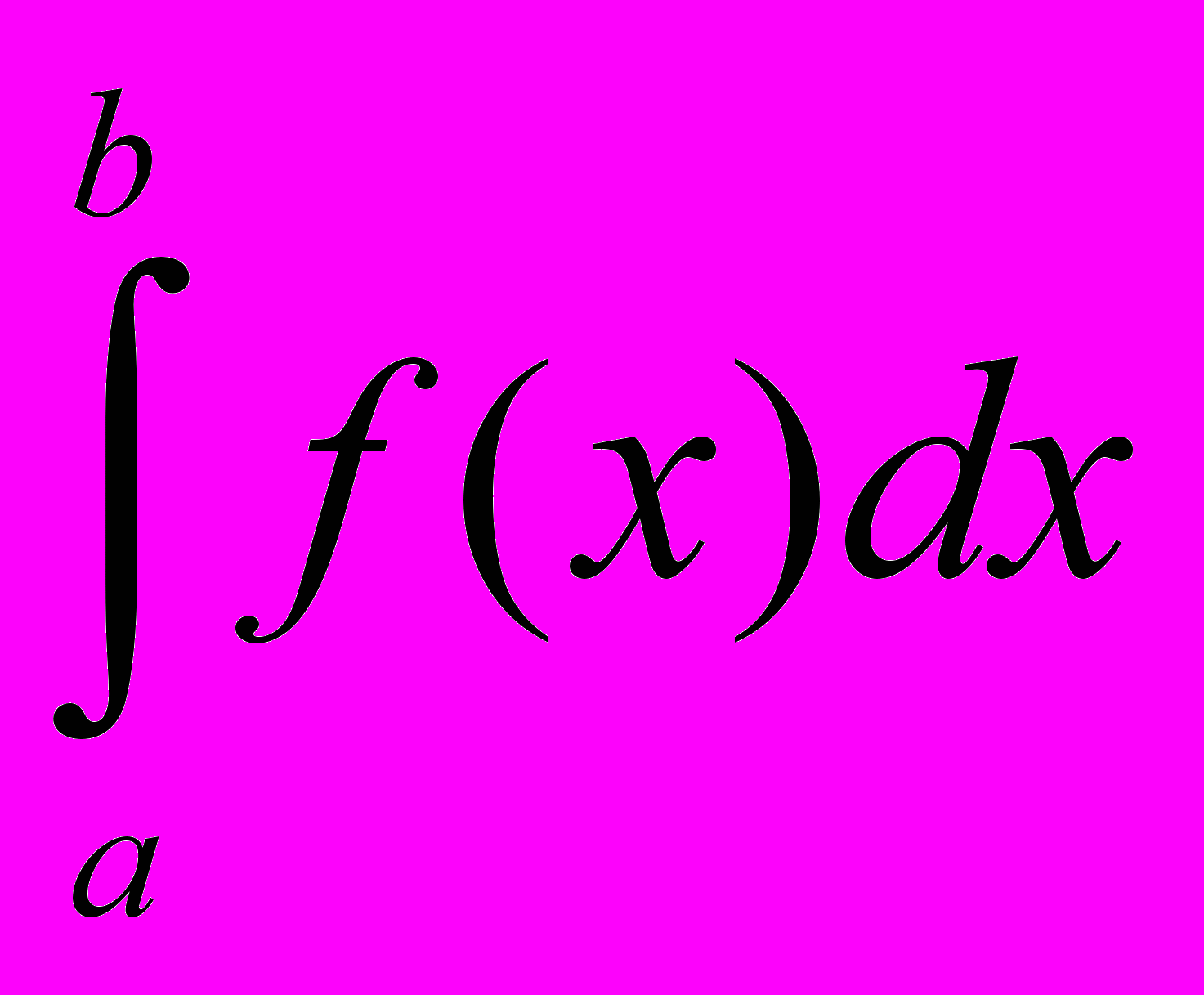буде від’ємний. Провівши попередні побудови, одержуємо відрізок b, величина якого від’ємна, і тут b= .

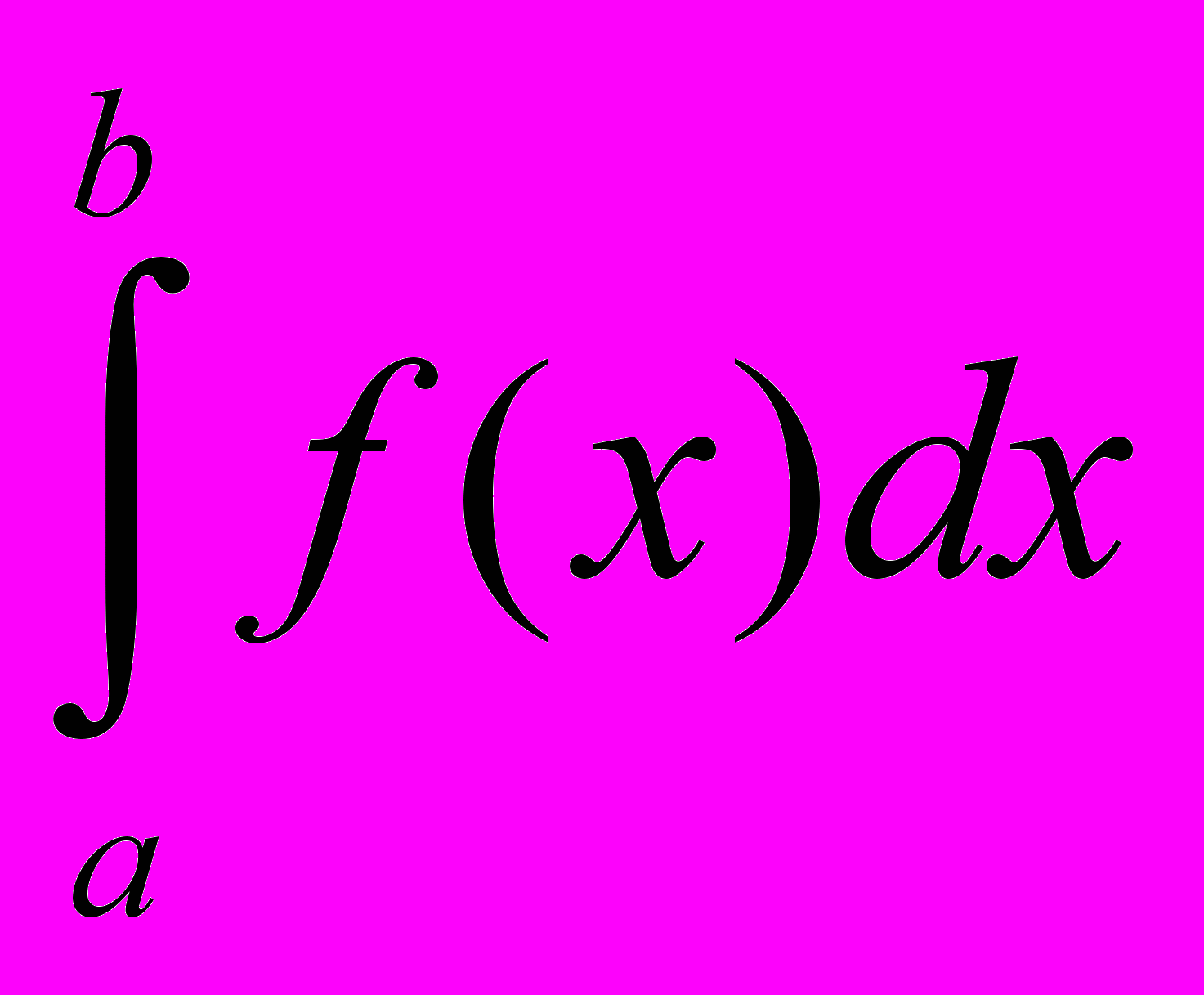На підставі проведеної побудови і здійснюється графічне інтегрування. Метод графічного інтегрування проілюстрований далі на прикладі.


Зразок виконання завдання.

Завдання. Функція представлена графічно на відрізку [0; b]=[0; 12]. Побудувати графік її інтеграла F(x)=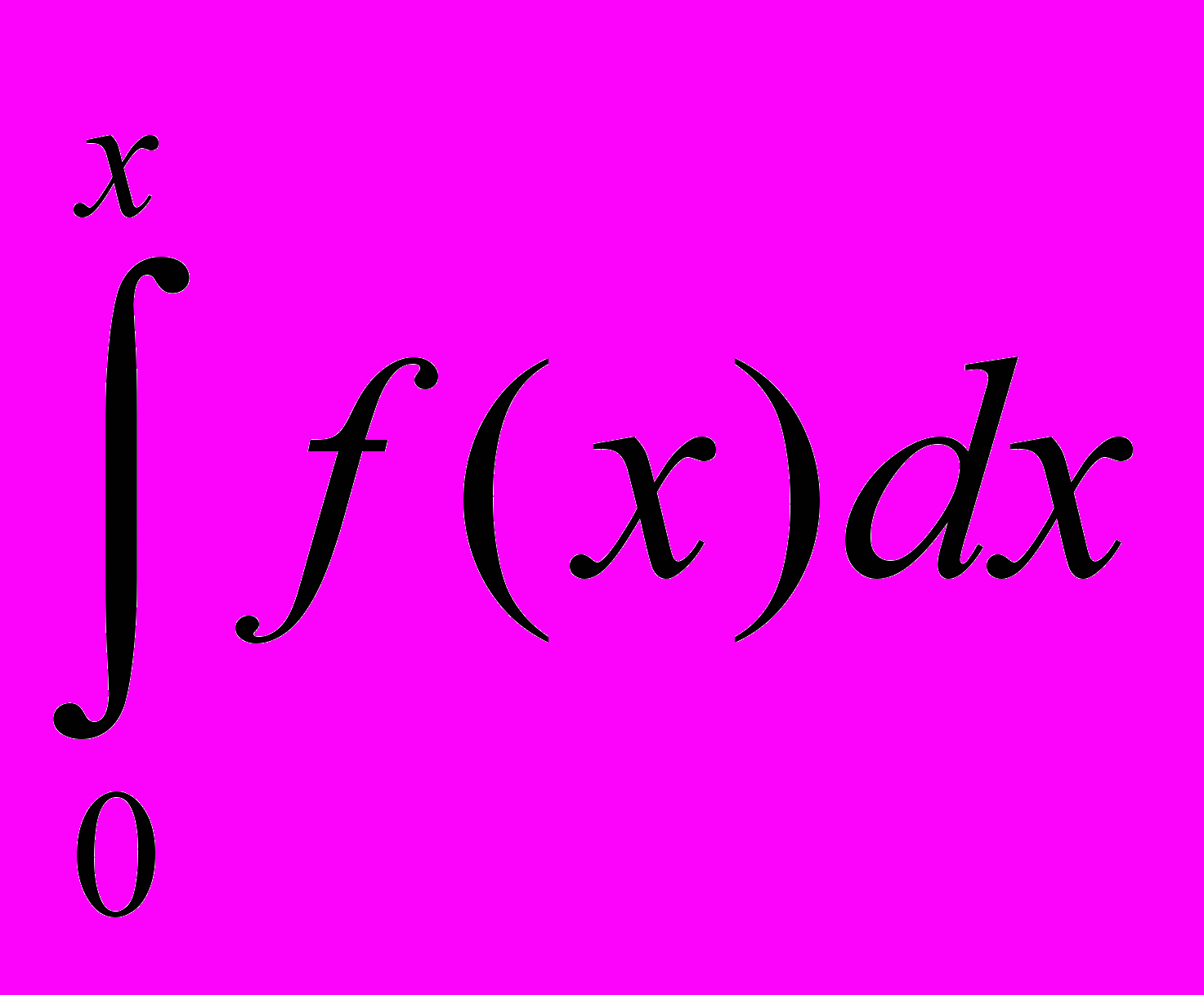, 0 ≤ x ≤ b. Визначити за графіком величину .

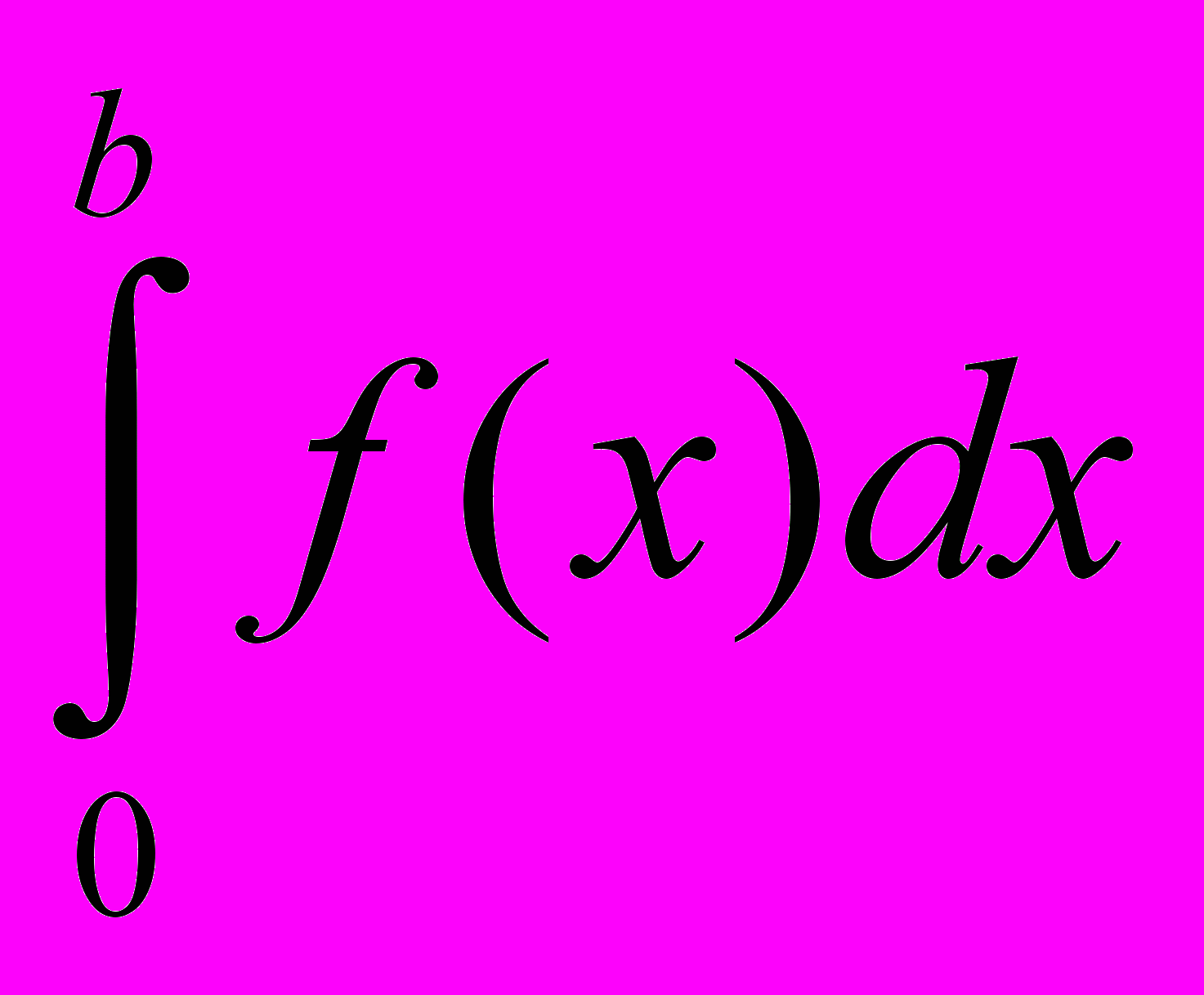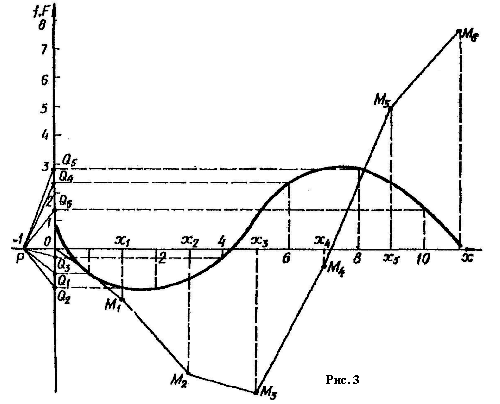
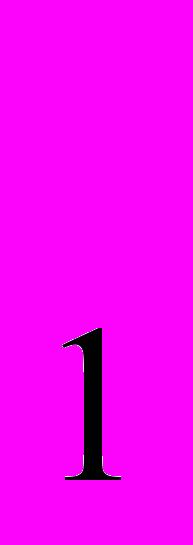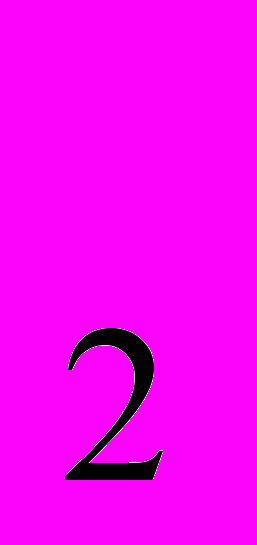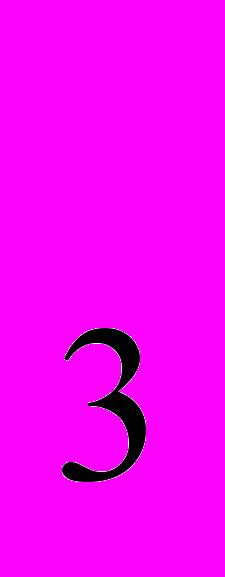Розв’язання. Розділимо відрізок [0; 12] на часткові відрізки (див. рис. 3). У даному прикладі взяті 6 часткових відрізків і точки поділу х=0, х, х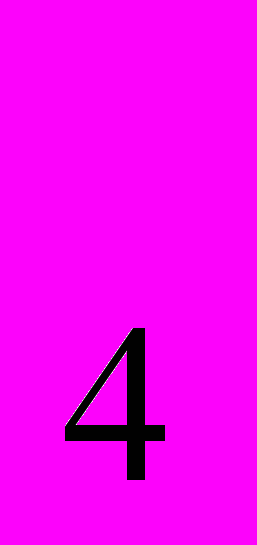, х, х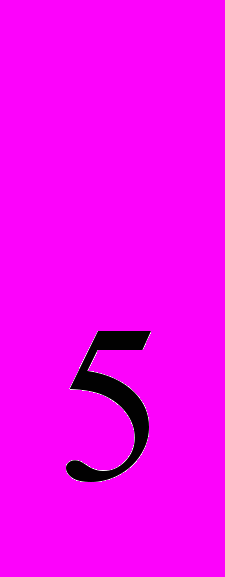, х, х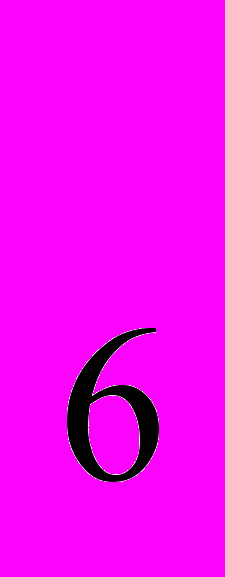=12 відзначені на рис. 3. Відкладаємо від точки О ліворуч по осі Ох одиничний відрізок. Визначаємо середину часткового відрізка 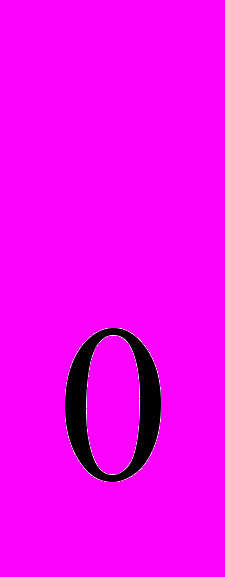[х; х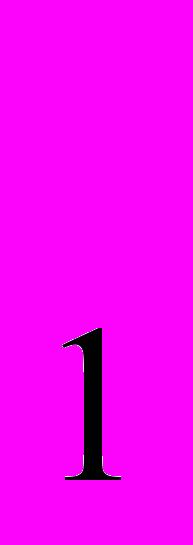 ] і ординату графіка функції f(x) у цій точці проектуємо на вісь Оу. Одержимо точку Q 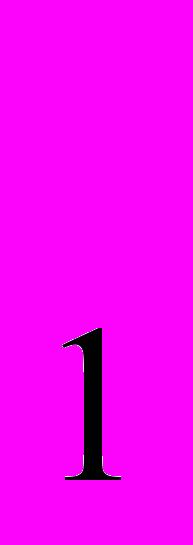. Проводимо РQ 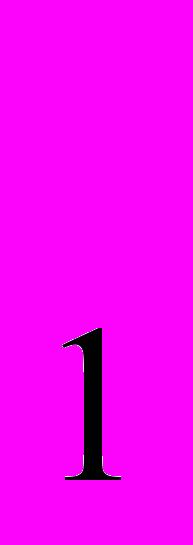, а потім ОМ 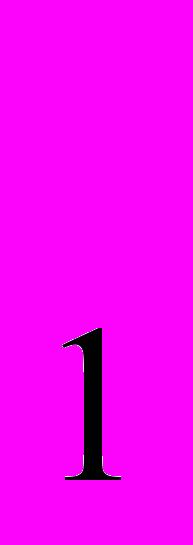паралельно РQ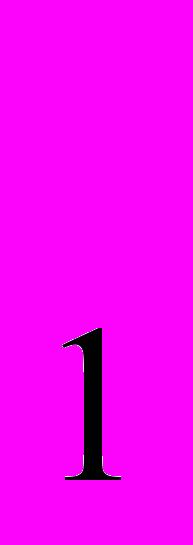. При цьому

х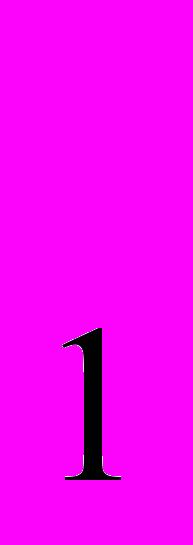М ≈.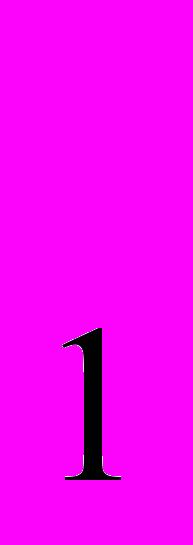

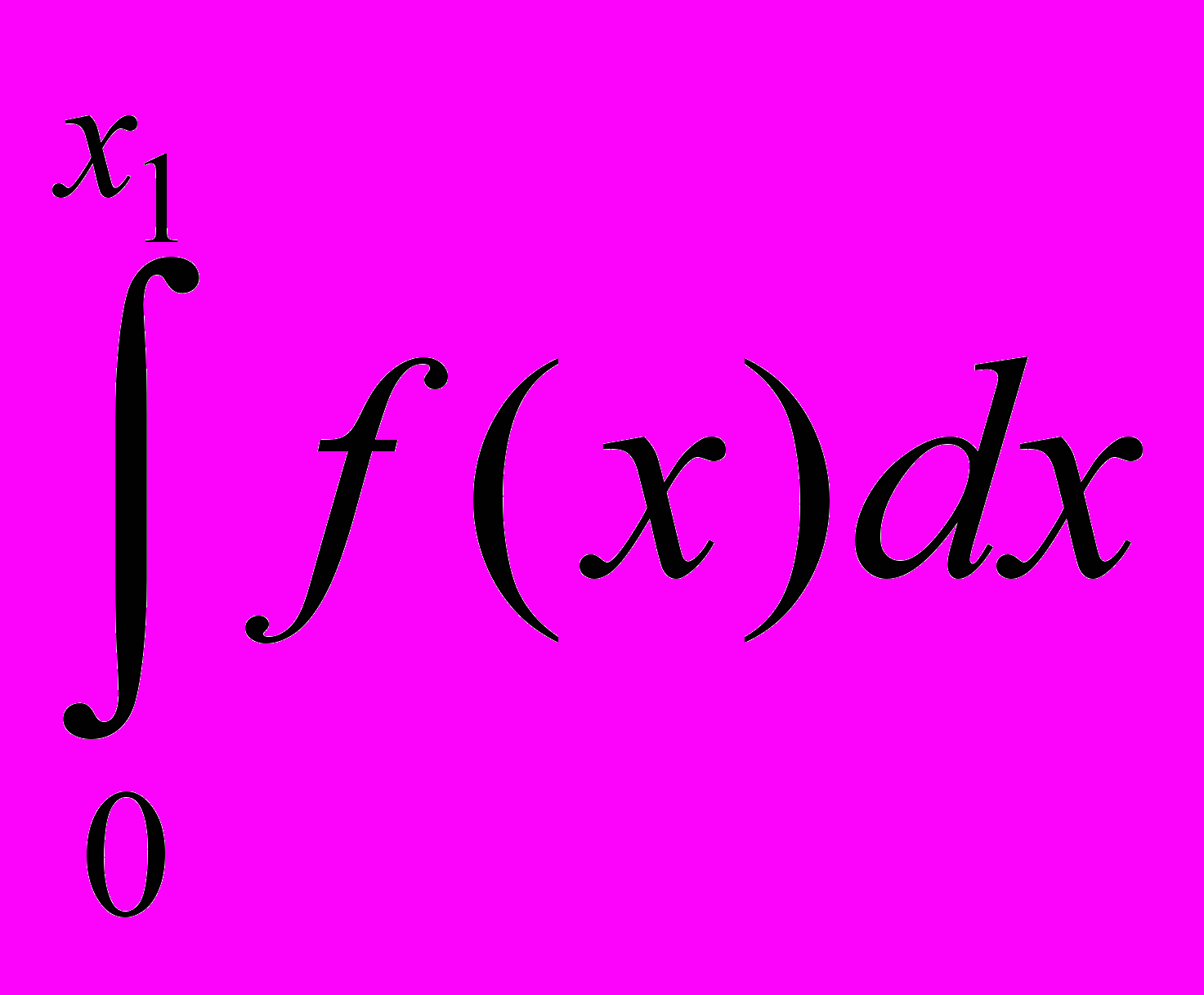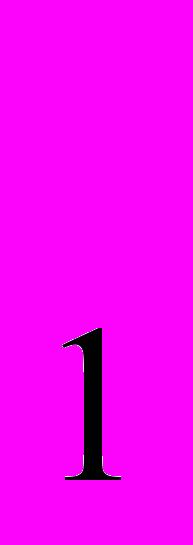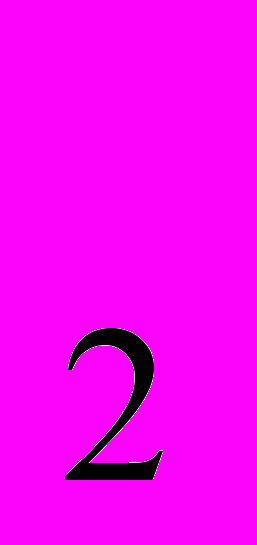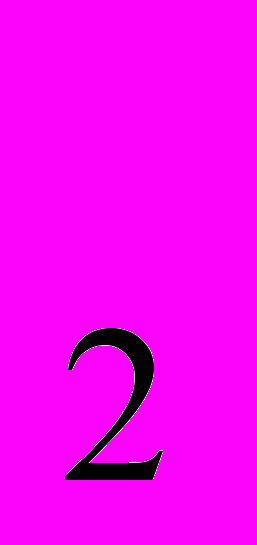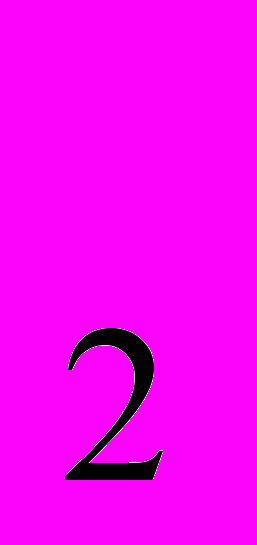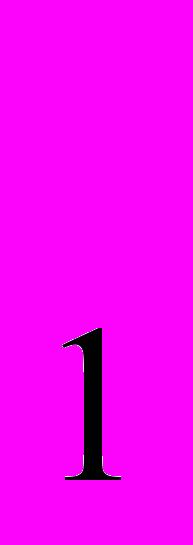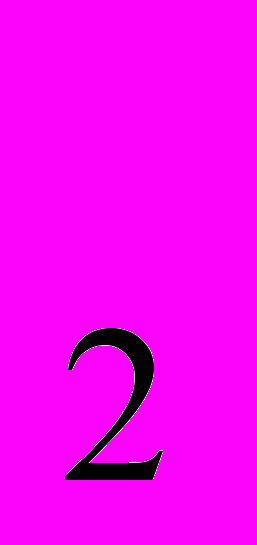Визначаємо середину часткового відрізка [х; х]. Ордината графіка в цій точці проектується на відрізок ОQ. З'єднуємо Р з Q і будуємо ММ ||РQ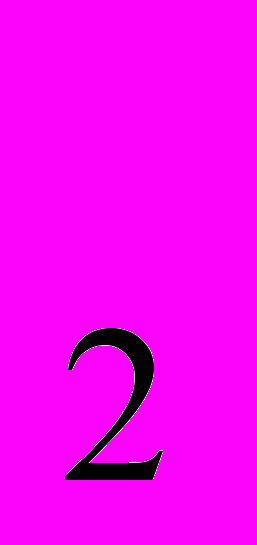. Тоді х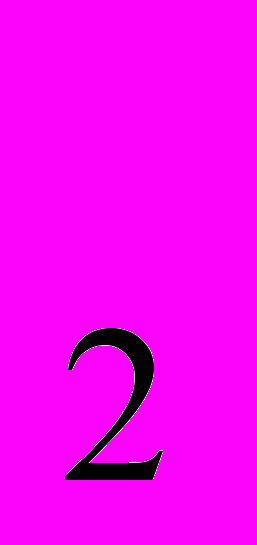М≈.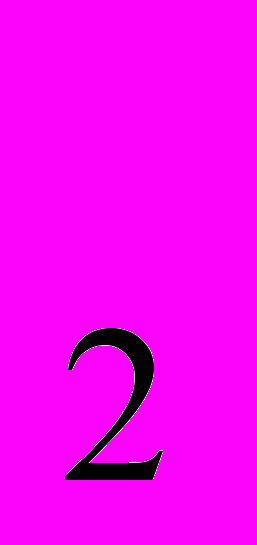

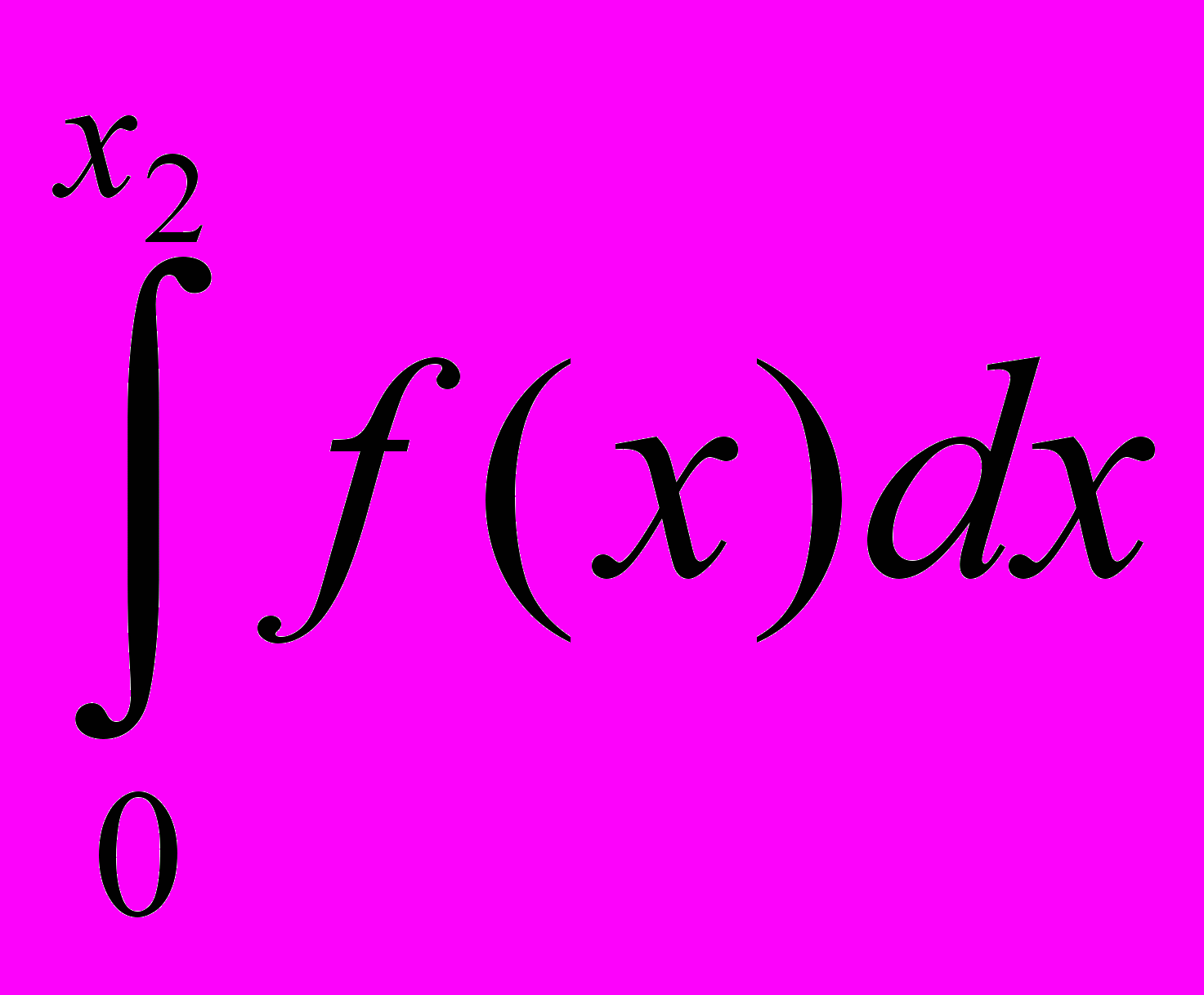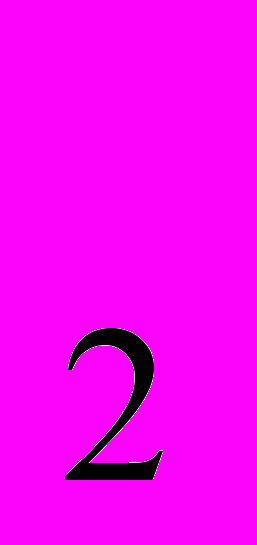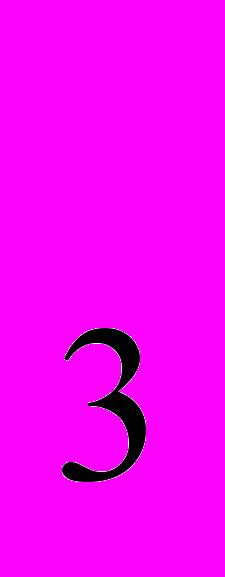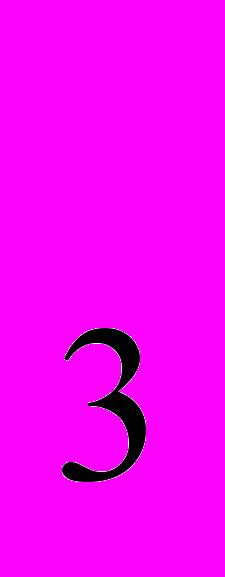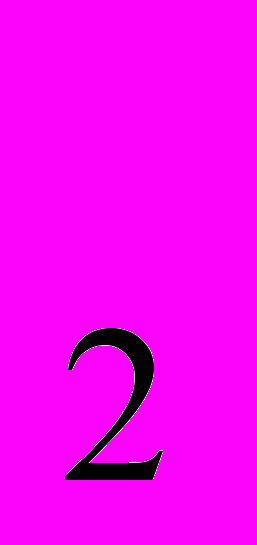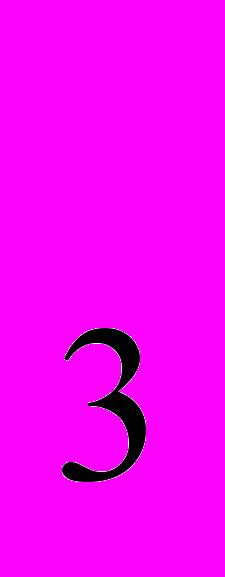Відзначаємо середину відрізка [х ; х ], потім ОQ і проводимо ММ ||РQ. Маємо хМ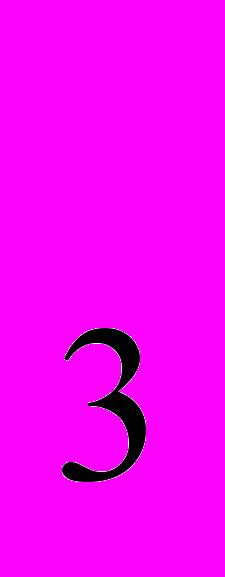≈ 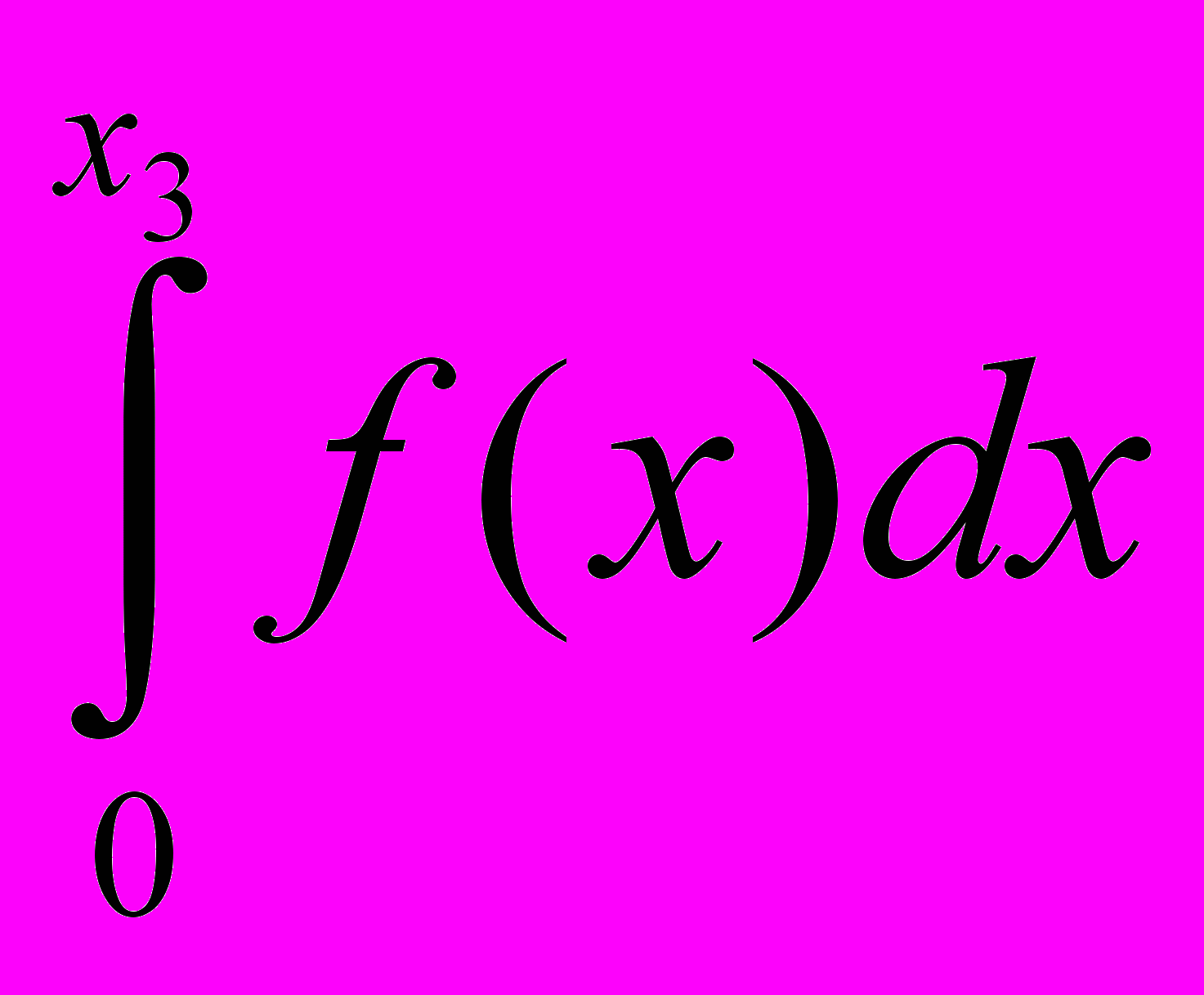і т.д., поки не одержимо точку М. 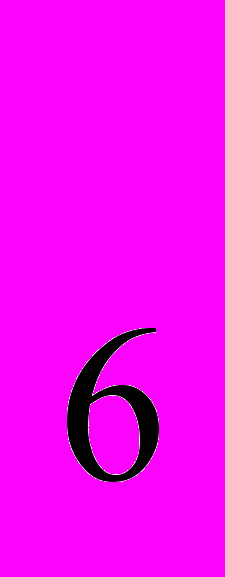Ламана О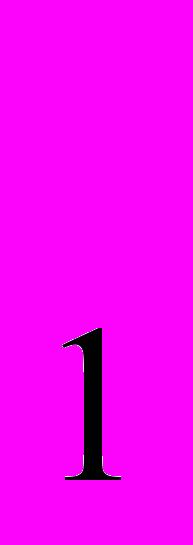М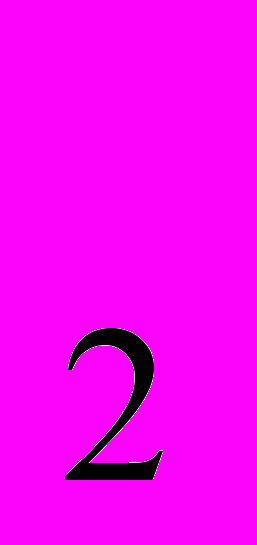М…М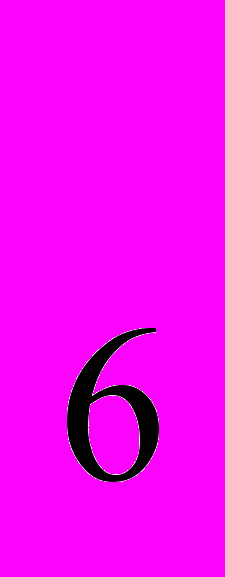 — графік первісної для функції, представленої на рис. 3.

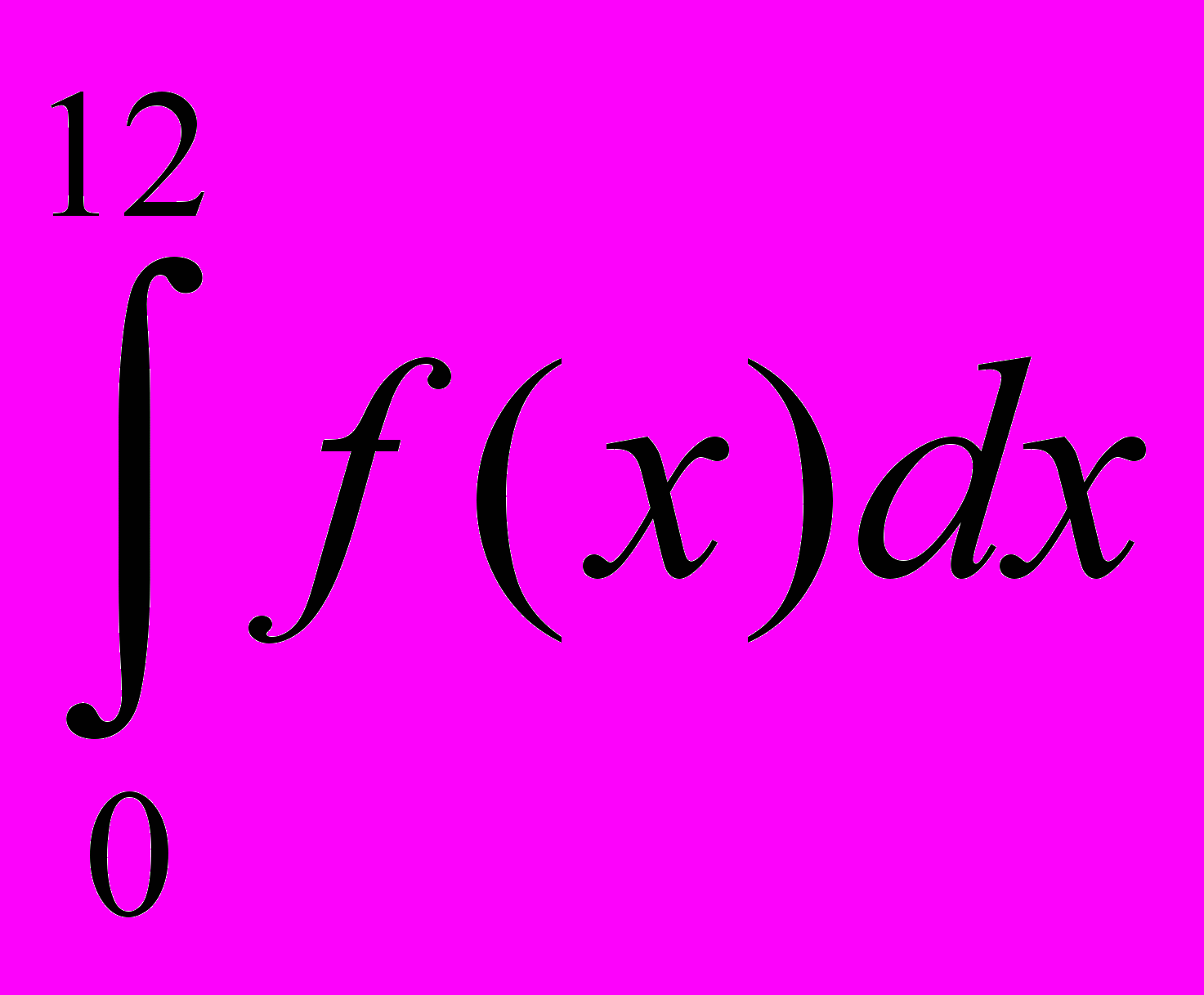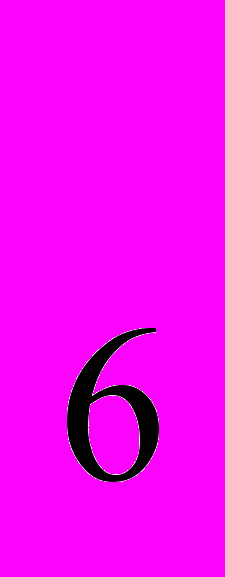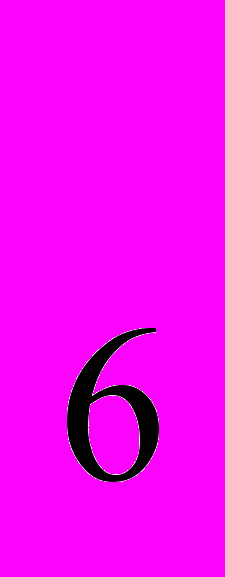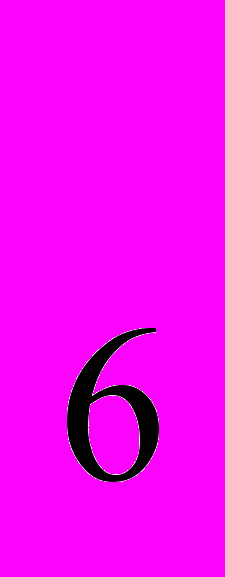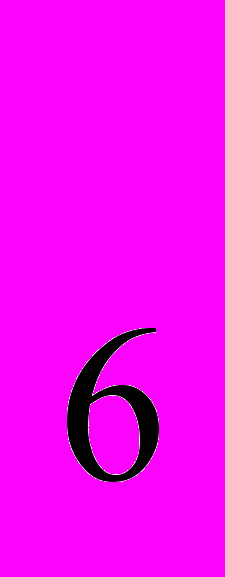Наближене значення дорівнює ординаті хМ. За графіком знаходимо х М ≈7,8.


Завдання для самостійної роботи

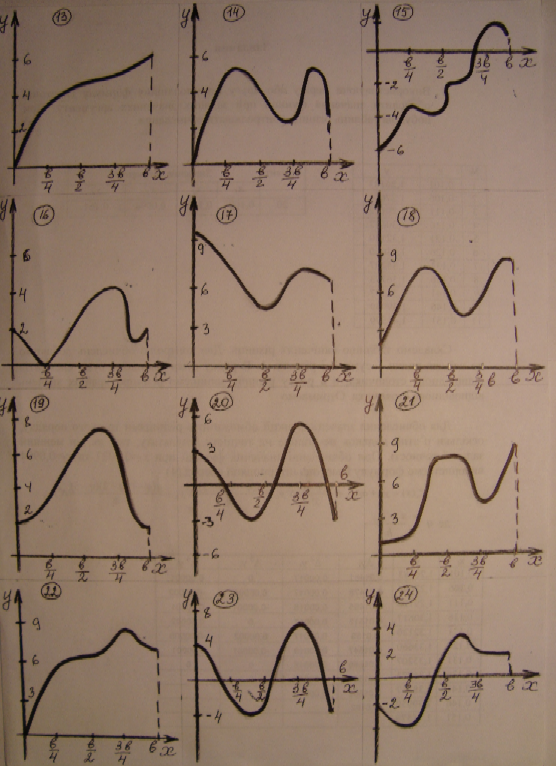
Функція задана графічно на відрізку [0; b]. Побудувати графік її інтеграла F(x)=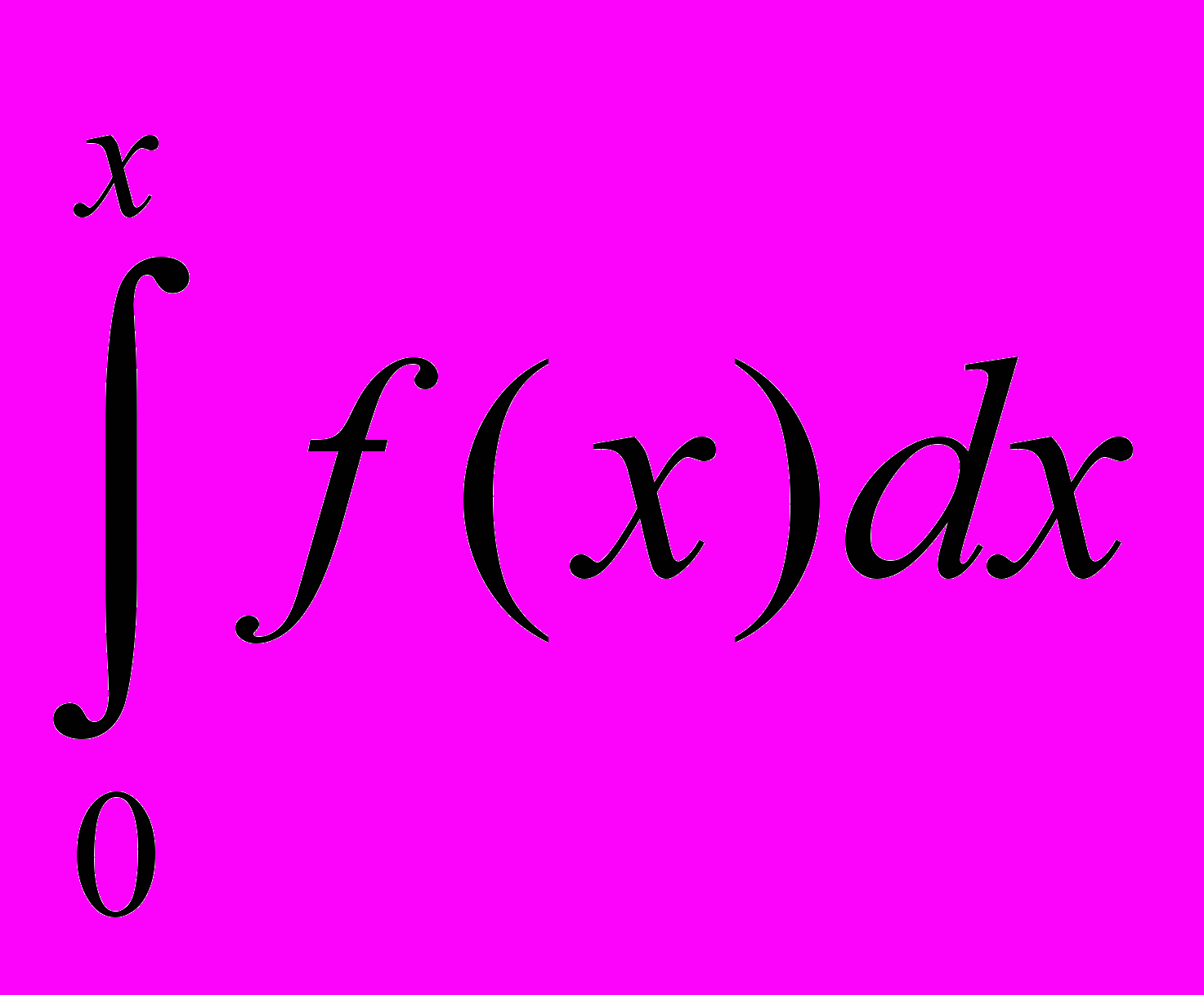, 0 ≤ x ≤ b. Визначити за графіком величину 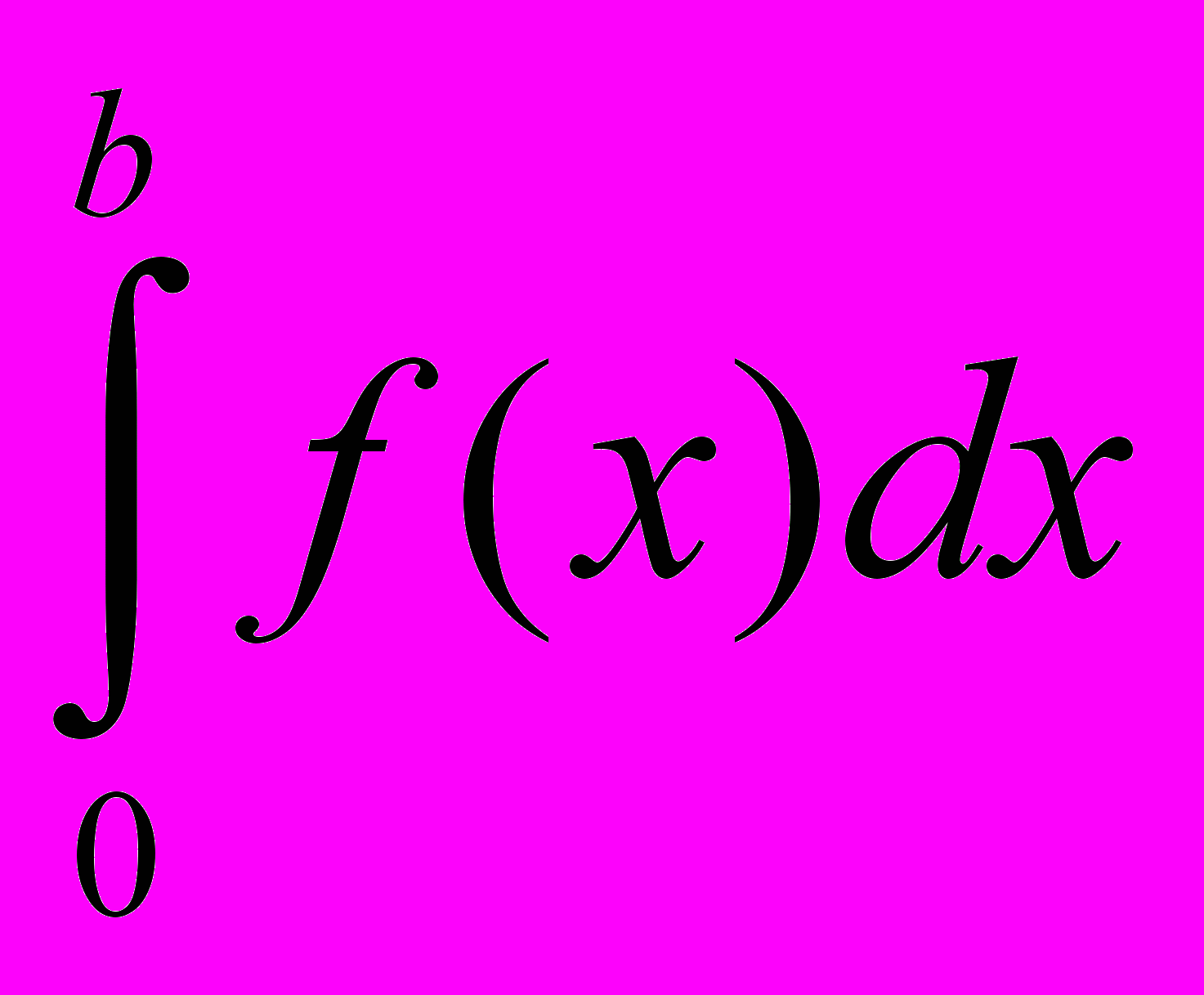. Значення b варто взяти з таб. 1.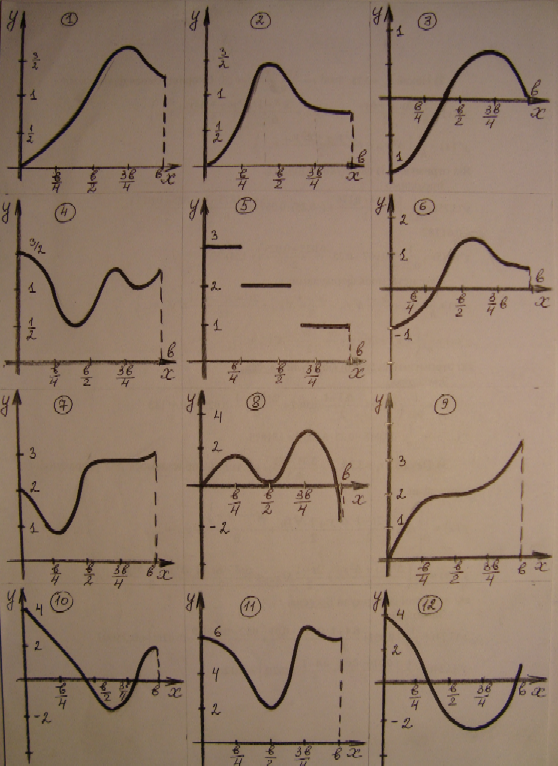











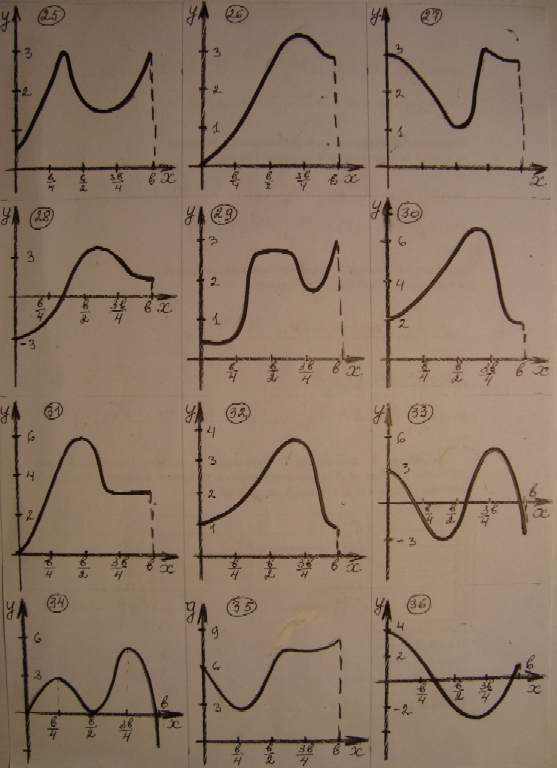
Таблиця 1

Варіант
b
Варіант
b
Варіант
b

1
4,4
13
9,2
25
6,8

2
4,8
14
9,6
26
7,2

3
5,2
15
10,0
27
7,6

4
5,6
16
10,4
28
8,0

5
6,0
17
10,8
29
8,4

6
6,4
18
11,2
30
8,8

7
6,8
19
11,6
31
10,4

8
7,2
20
12,0
32
10,8

9
7,6
21
12,4
33
11,2

10
8,0
22
12,8
34
11,6

11
8,4
23
13,2
35
12,0

12
8,8
24
13,6
36
12,4