P. у таблиці 1 наведено математичні сподівання густини пресовок за різних тисків пресування – від 100 до 700 мпа. Графічне зображення експериментальних даних, наведене на рисунку 1, дає змогу передбачити наявність лінійної кореляційної залежності г/см
| Вид материала | Документы |
СодержаниеТаблиця 1 Вихідні дані та допоміжні розрахунки Допоміжні дані |
- Могилянська Академія " Реферат з курсу, 44.73kb.
- Комп’ютерна графіка, 233.55kb.
- Інтерфейс системи керування базами даних access. Створення бази даних. Таблиці. Запити, 156.05kb.
- А. М. Тема V, 524.73kb.
- Як перевірити наявність коду imei телефону у базі даних кодів imei, 61.57kb.
- Назва реферату: Оформлення документації по оприбуткуванню готової продукції Розділ, 129.19kb.
- Сенюра оксана володимирівна, 25.32kb.
- Методичні рекомендації до вивчення теми 4 Державний стандарт освіти «Бази даних. Системи, 1008.1kb.
- Роботу з об'єктами, до яких відносяться таблиці бази даних, запити, а також об'єкти, 623.25kb.
- Способи формування та характеристики зображення, 72.17kb.
ДО УВАГИ СТУДЕНТІВ!!!
Шановні студенти, велике прохання до Вас, дуже поважно віднесіться до виконання контрольної роботи.
В даному файлі знаходиться приклад розрахункового завдання та після прикладу наведені необхідні формули для його розрахунку.
Як оформлено цей приклад, так і повинно бути оформлена розрахункова частина у Вашій контрольній роботі.
Приклад синтезу лінійної регресійної моделі
Розглянемо приклад синтезу лінійної регресійної моделі за даними експериментального дослідження залежності густини пресовок із порошку міді γ від тиску пресування P. У таблиці 1 наведено математичні сподівання густини пресовок за різних тисків пресування – від 100 до 700 МПа. Графічне зображення експериментальних даних, наведене на рисунку 1, дає змогу передбачити наявність лінійної кореляційної залежності
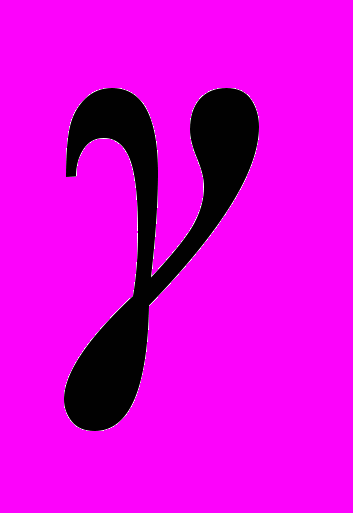 (г/см3) від Р(МПа).
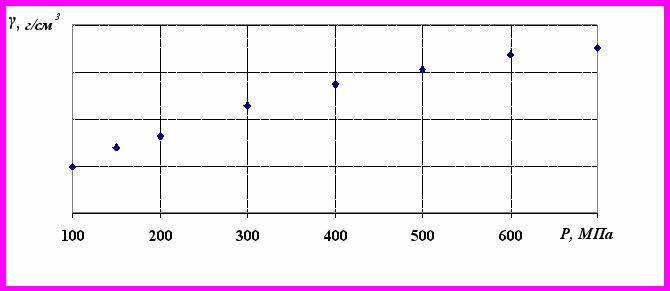
(г/см3) від Р(МПа).Вихідні дані для обчислення коефіцієнтів рівняння регресії і допоміжні розрахунки наведено в табл.1 і графічно зображено на рисунку 1.
4
5
6
7
Рис 1. Вихідні дані залежності густини пресовок
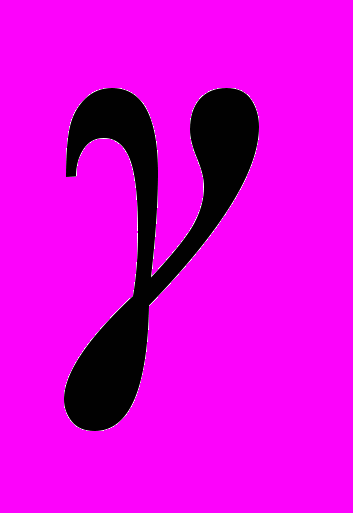 від тиску пресування Р
від тиску пресування РВиконуємо обчислення коефіцієнтів рівняння регресії за формулами (6.8) і 6.9).
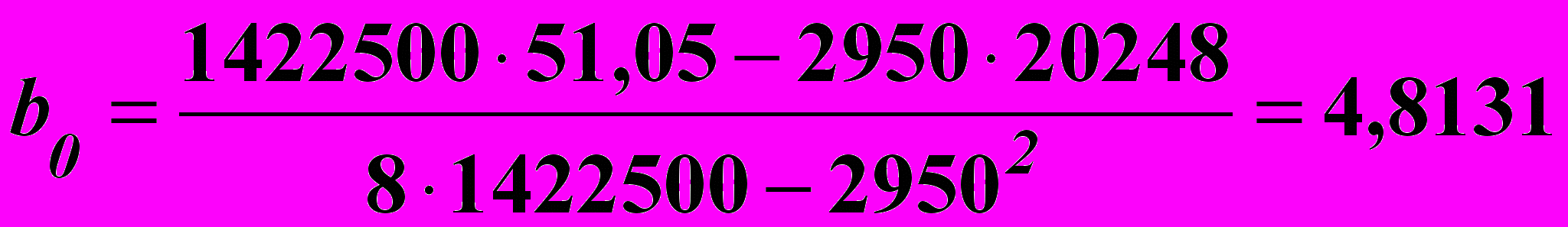 ;
;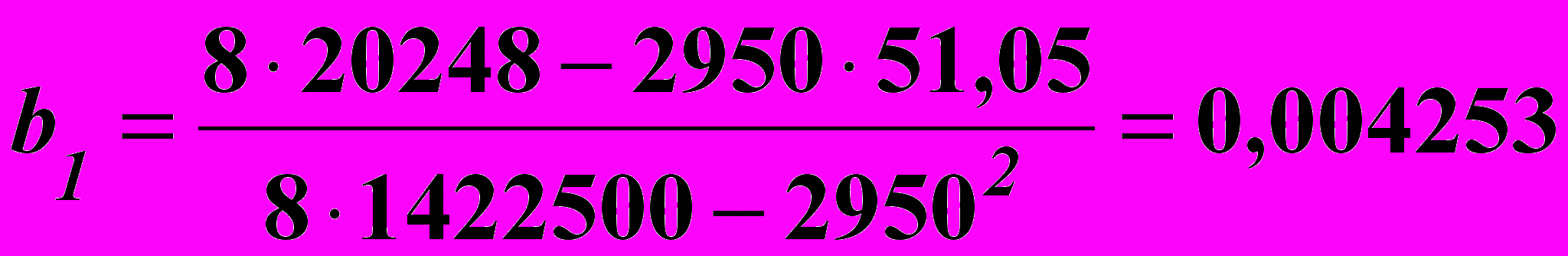 .
.Таблиця 1
Вихідні дані та допоміжні розрахунки
| № досліду | Тиск Р, МПа | Густина 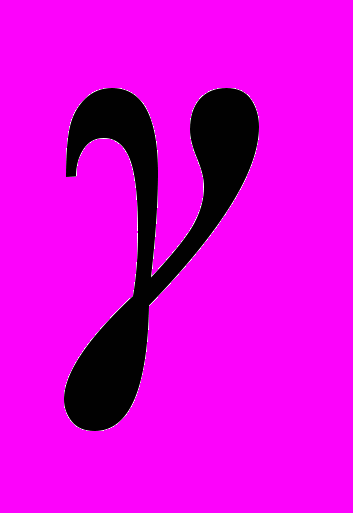 , г/см3 , г/см3 | Допоміжні дані | ||||
| хi |  | yi | 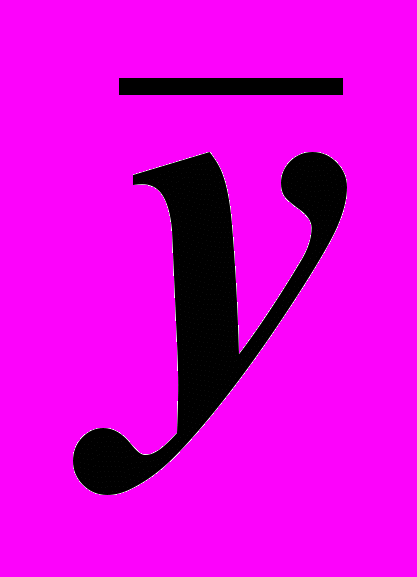 | xi yi | 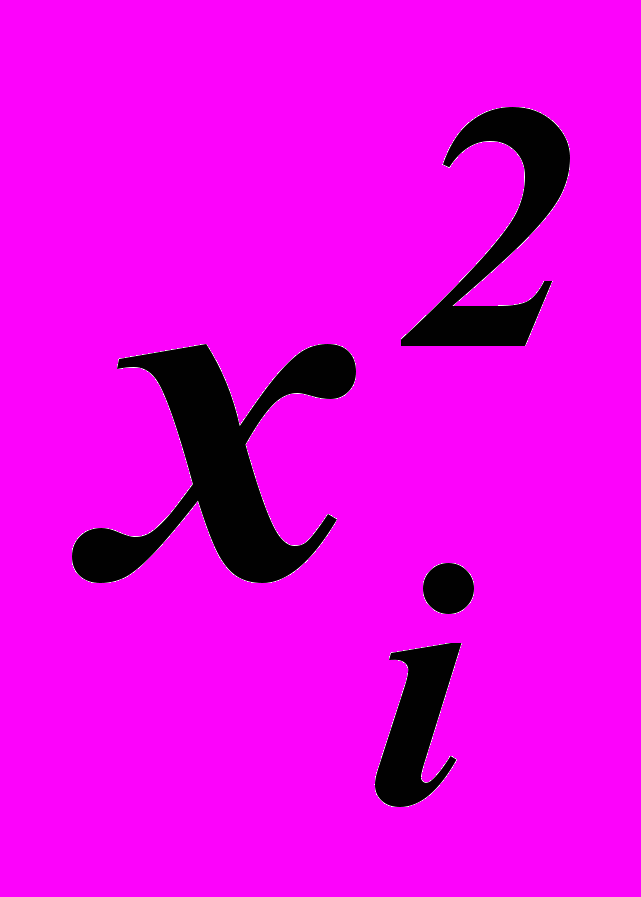 | 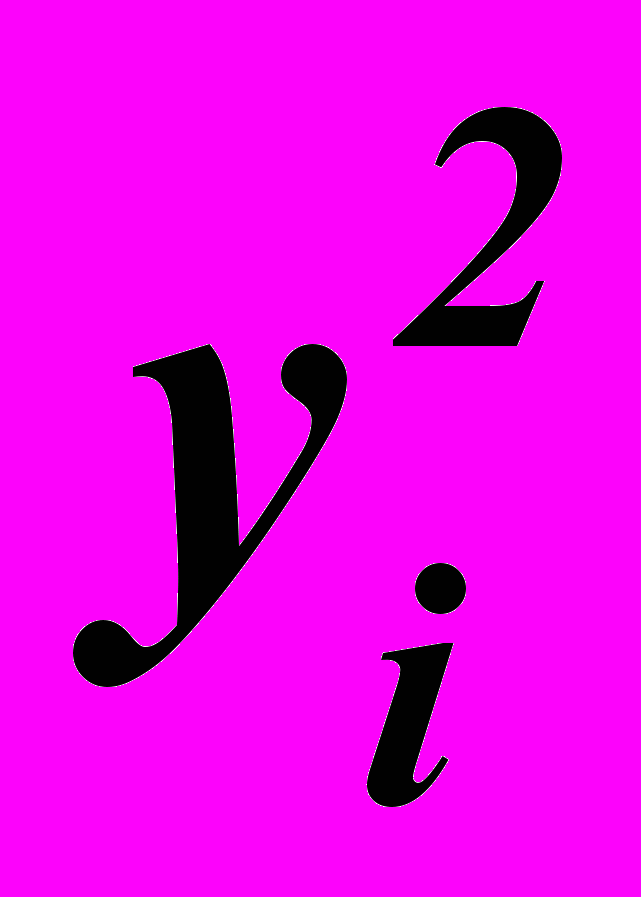 | |
| 1 | 100 | 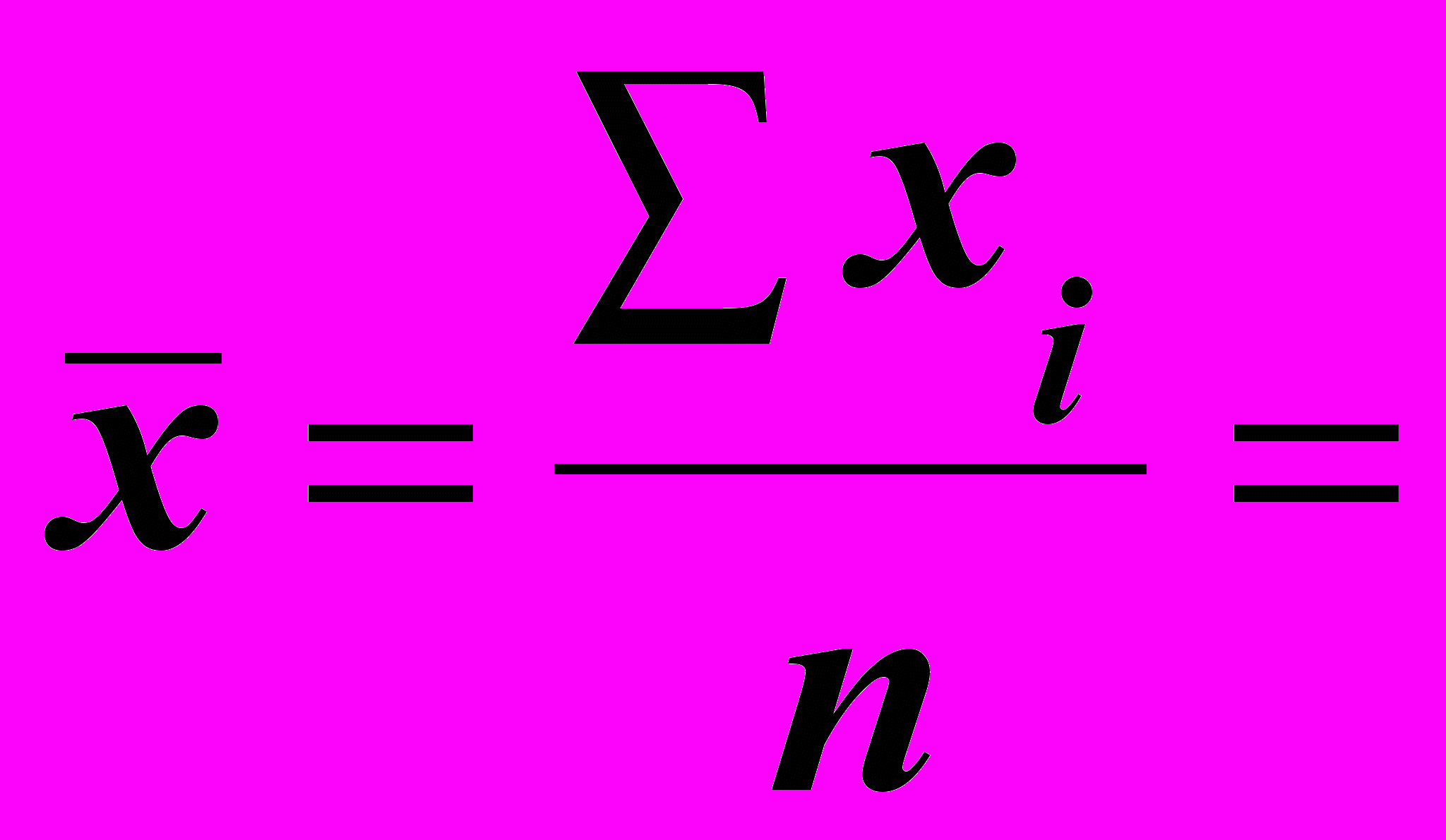 = 368,75 | 5,00 | 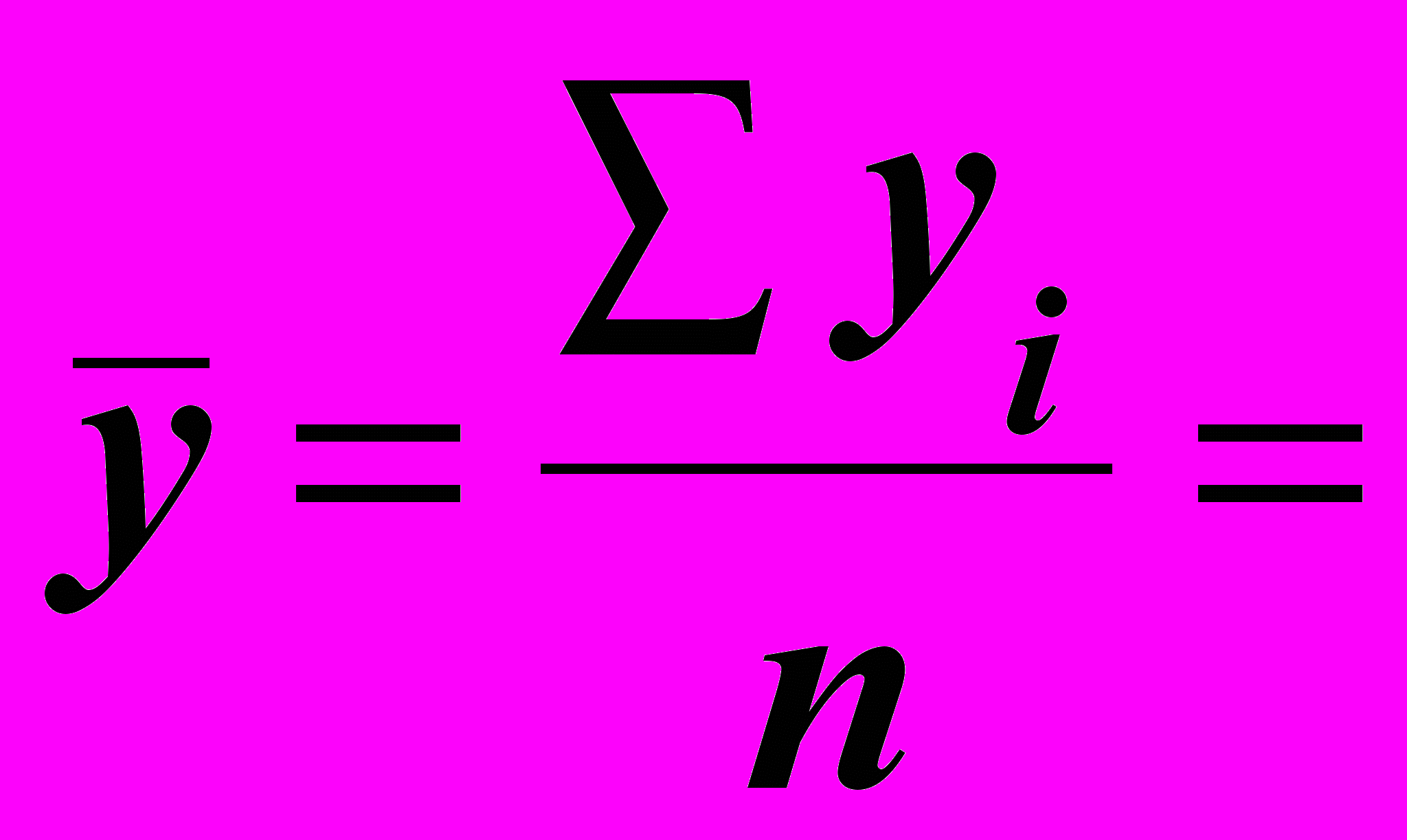 6,38125 6,38125 | 500 | 10000 | 25,0000 |
| 2 | 150 | 5,40 | 810 | 22500 | 29,1600 | ||
| 3 | 200 | 5,65 | 1130 | 40000 | 31,9225 | ||
| 4 | 300 | 6,30 | 1890 | 90000 | 39,6900 | ||
| 5 | 400 | 6,74 | 2696 | 160000 | 45,4276 | ||
| 6 | 500 | 7,06 | 3530 | 250000 | 49,8436 | ||
| 7 | 600 | 7,38 | 4428 | 360000 | 54,4644 | ||
| 8 | 700 | 7,52 | 5264 | 490000 | 56,5504 | ||
| n = 8 |  = 2950 = 2950 | | 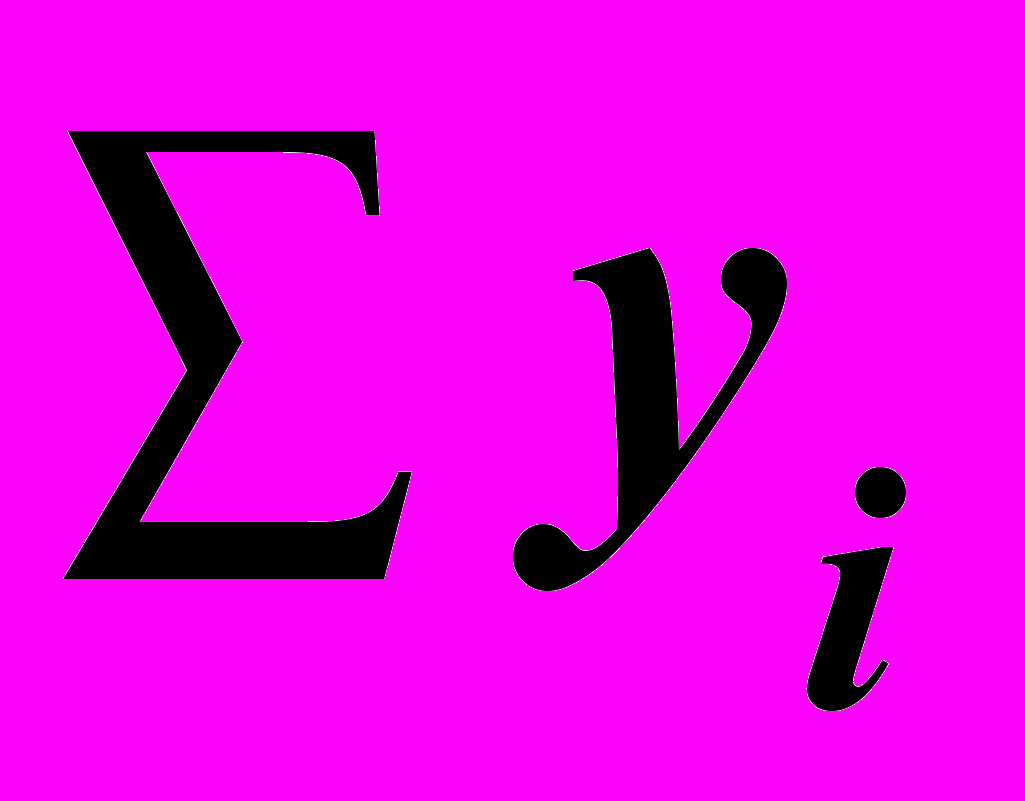 = 51,05 = 51,05 | | 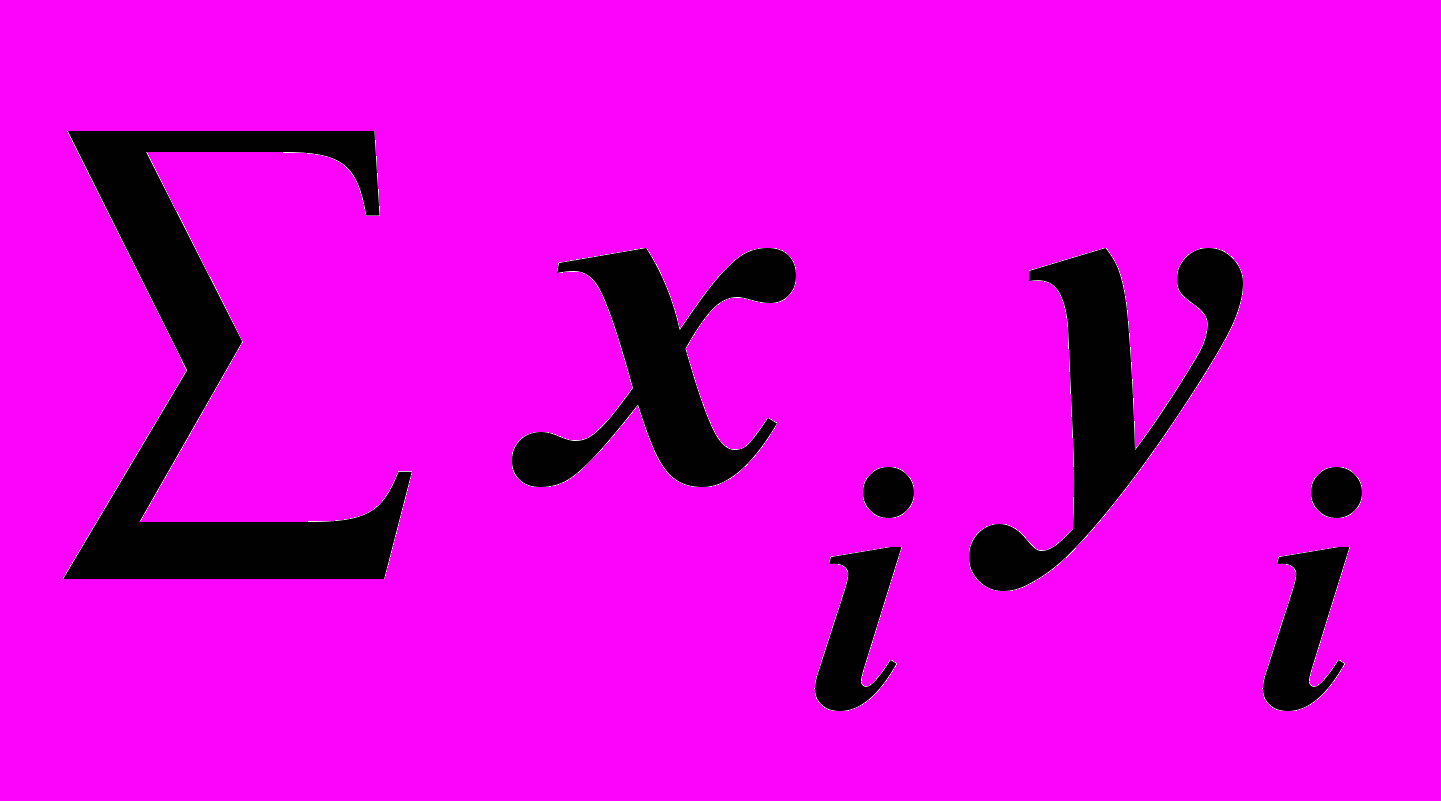 = 20248 = 20248 | 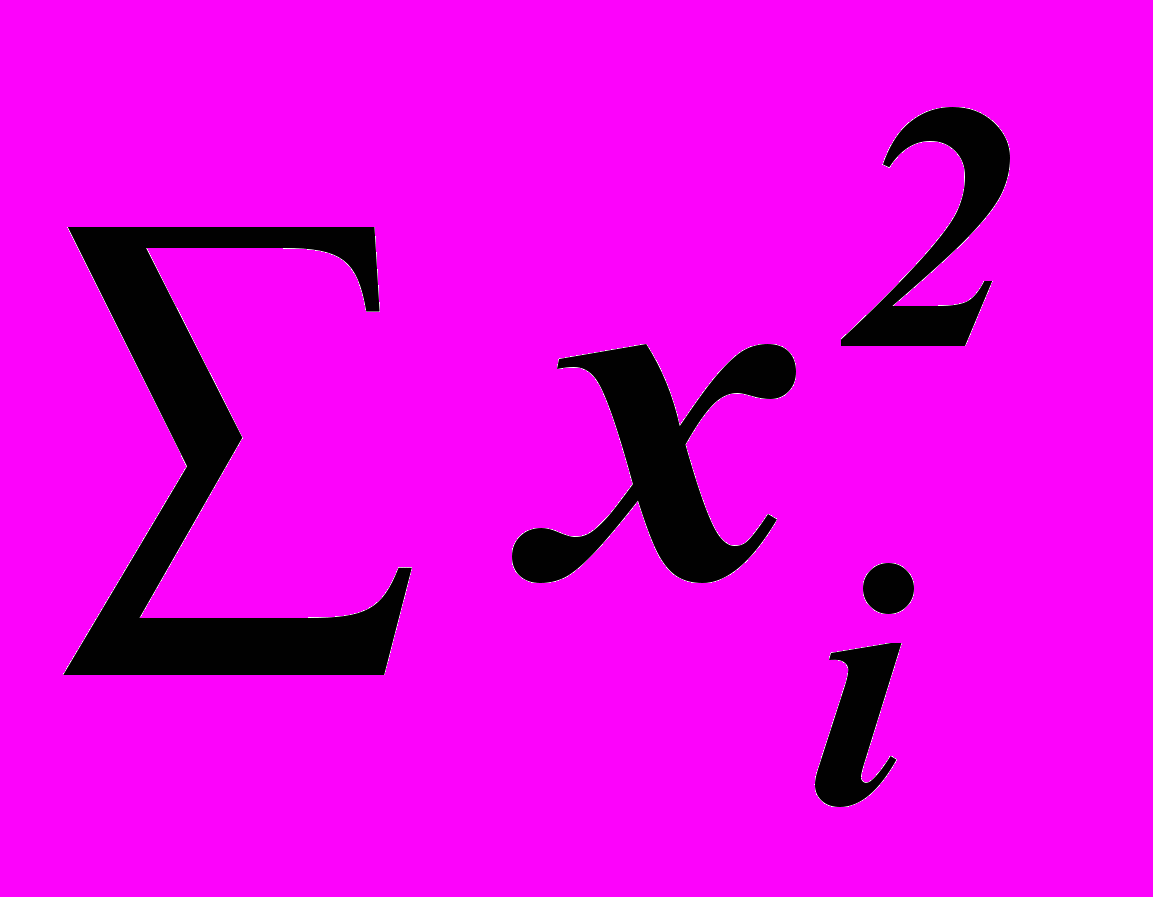 = 1422500 = 1422500 |  = 332,0585 = 332,0585 |
Щоб перевірити гіпотезу про статистичну значущість коефіцієнтів рівняння регресії, виконуємо обчислення значень критерію tрозрах. за формулою (6.10), заздалегідь визначивши величину стандартної похибки коефіцієнтів рівняння регресії за формулою (6.11).
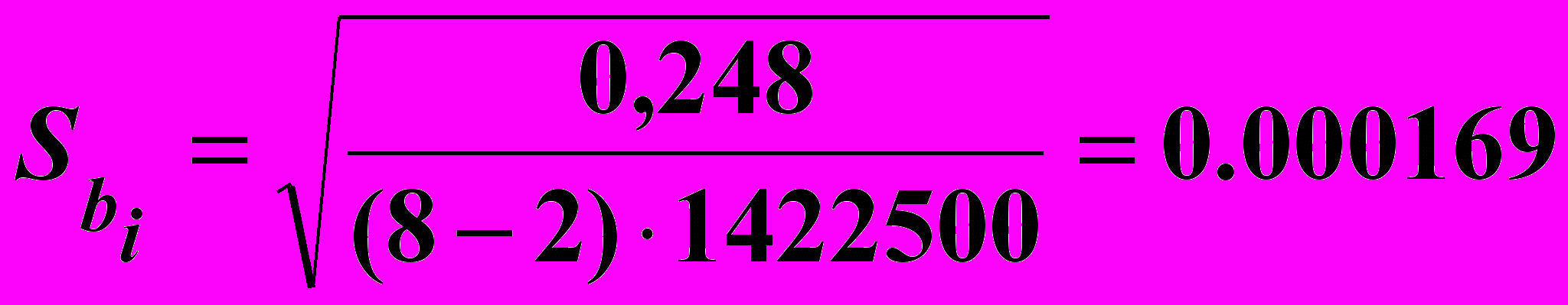 ;
;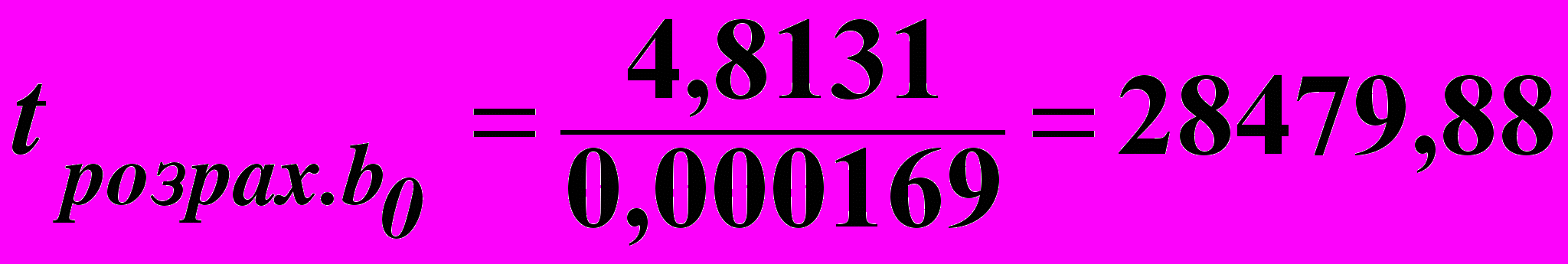 ;
;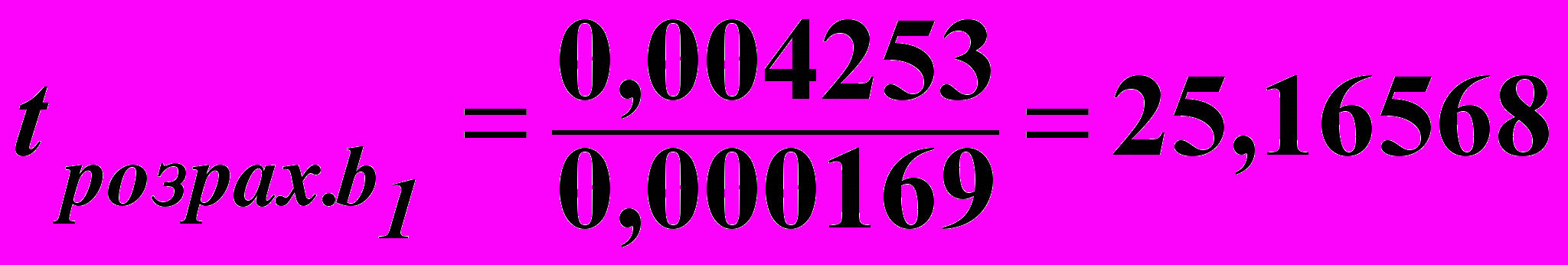 .
.Розрахункові значення коефіцієнтів
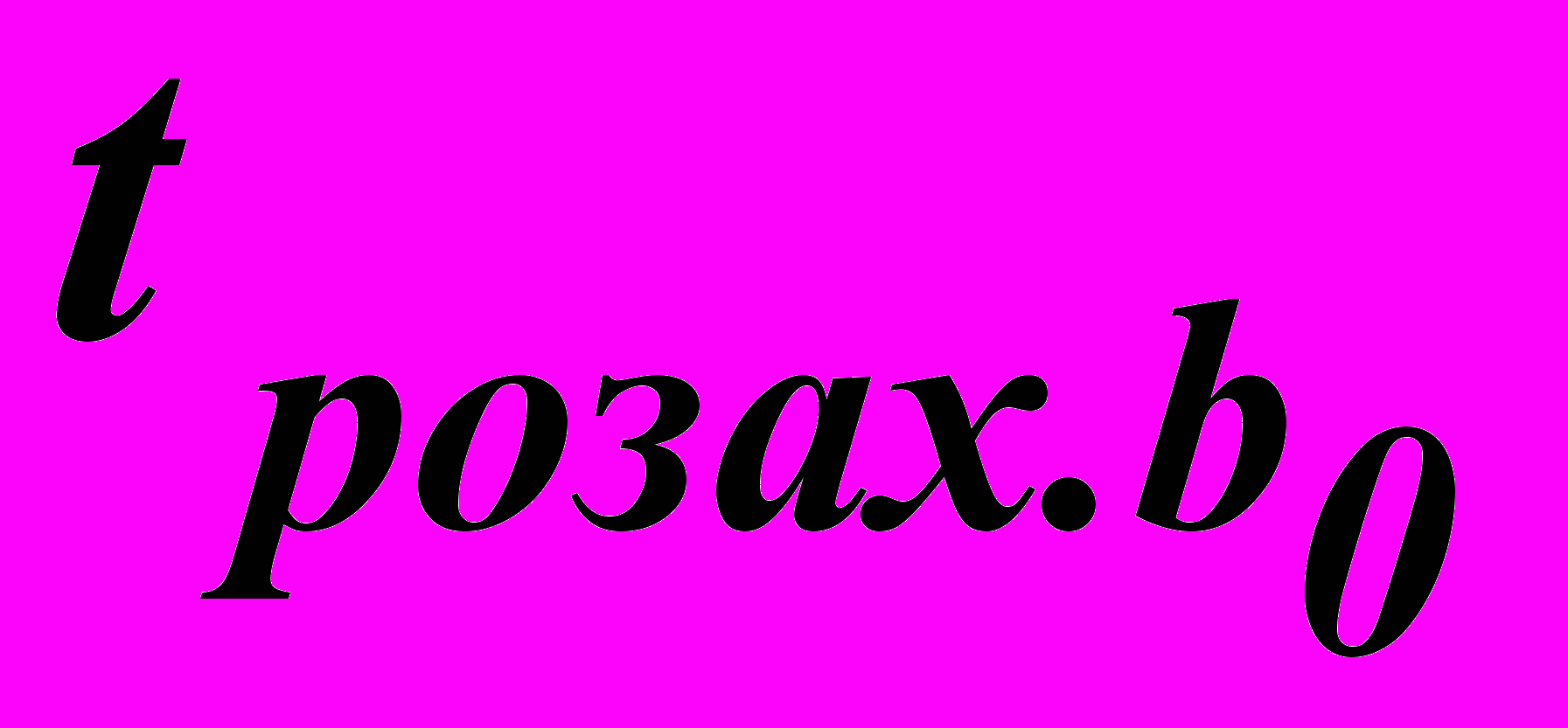 і
і 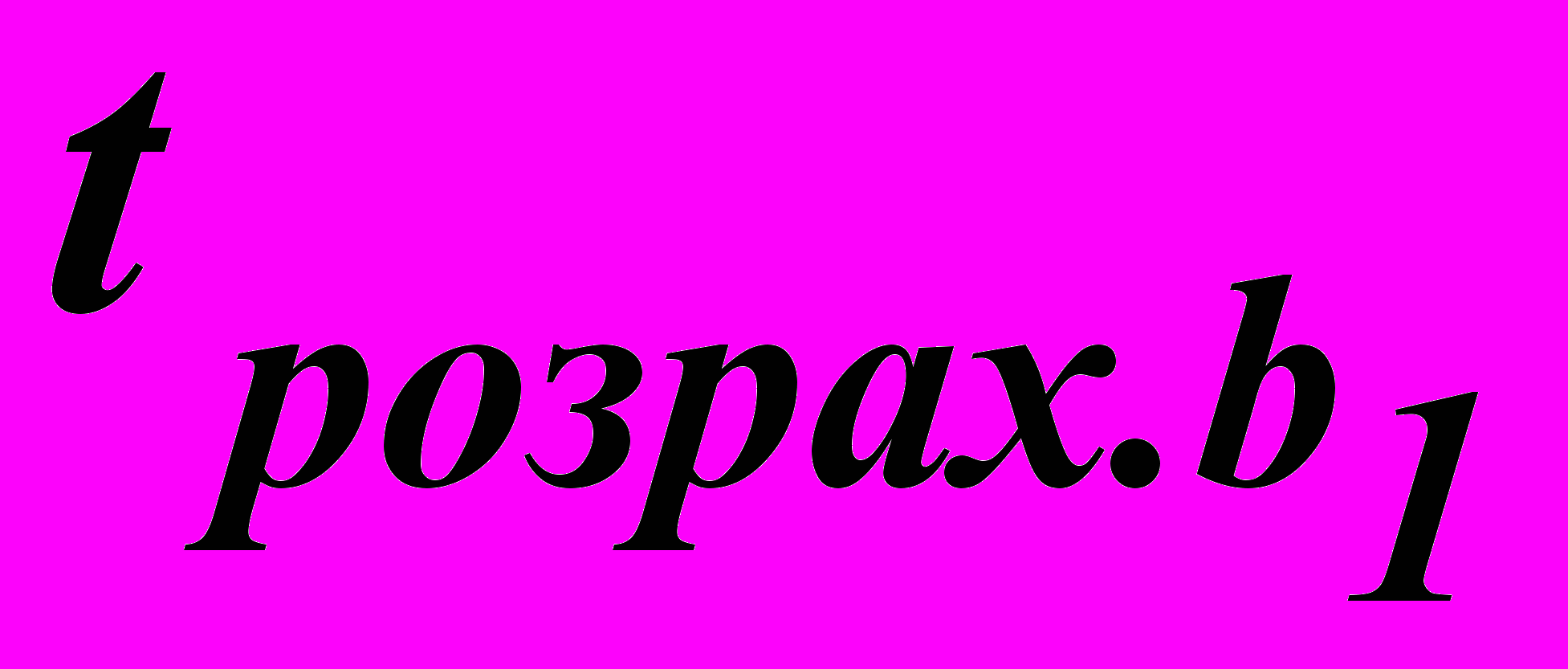 перевищують табличне, що дорівнює 2,45 при рівні значущості
перевищують табличне, що дорівнює 2,45 при рівні значущості = 0,05 та числі степенів свободи f = n – 2 = 6. Отже, коефіцієнти рівняння регресії b0 і b1 статистично значущі.
Можна записати лінійне рівняння регресії:
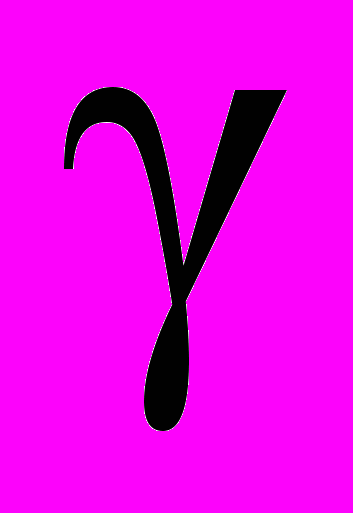 = 4,8131 + 0,004253 Р, г/см3 .
= 4,8131 + 0,004253 Р, г/см3 .На рисунку 2 графічно зображено результати вимірювань густини пресовок (їх математичні сподівання) при різних тисках пресування і нанесено лінію регресії
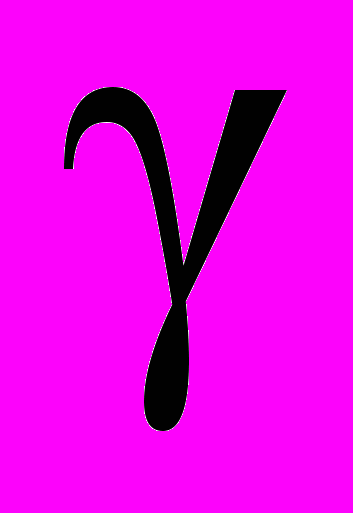 на Р відповідно до виконаних обчислень параметрів її рівняння.
на Р відповідно до виконаних обчислень параметрів її рівняння.Визначаємо величину коефіцієнта парної кореляції за формулою (6.18).
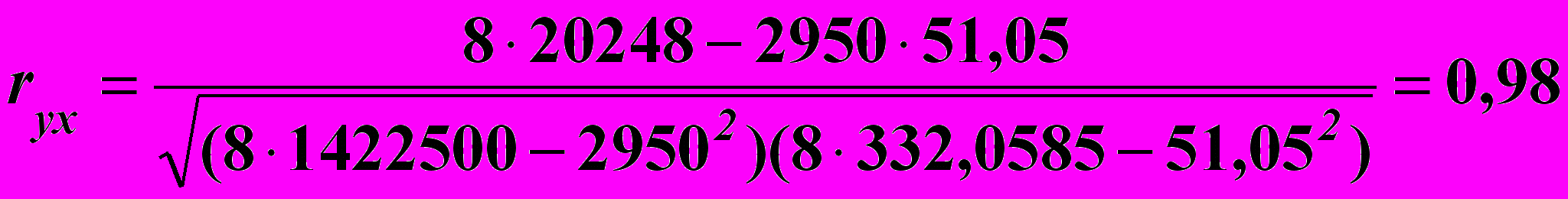 .
.Оскільки коефіцієнт ryx близький до одиниці, можна, навіть не виконуючи перевірки його статистичної значущості, зробити висновок про наявність щільного лінійного кореляційного зв’язку параметрів
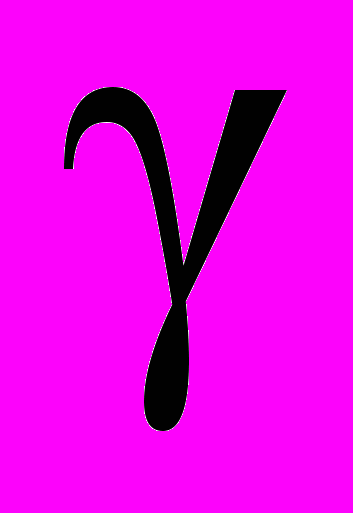 і Р.
і Р.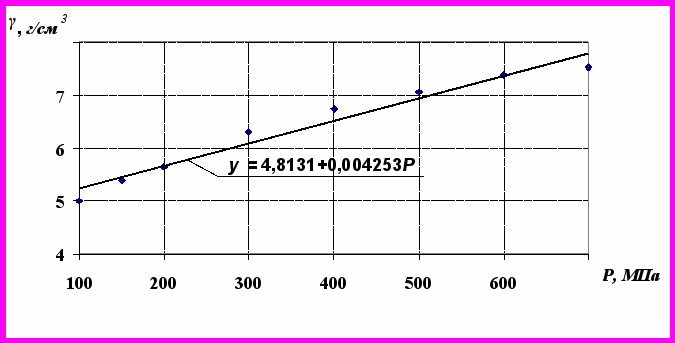
Рис 2. Залежність густини пресовок
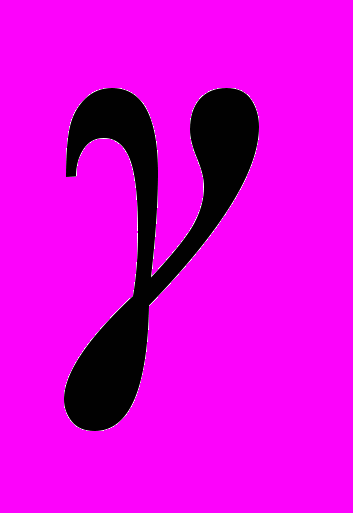
від тиску пресування Р
Для перевірки гіпотези про адекватність одержаного рівняння регресії експериментальним даним виконуємо обчислення величини критерію Фішера Fрозрах., використовуючи допоміжні дані, наведені в таблиці 3.
Таблиця 3
Дані допоміжних розрахунків для обчислення Fрозрах.
| xi | yi | 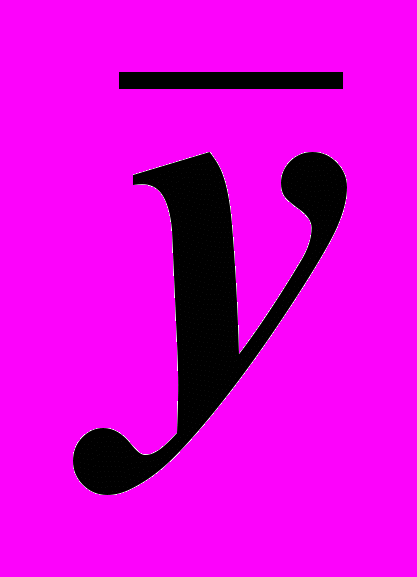 |  | 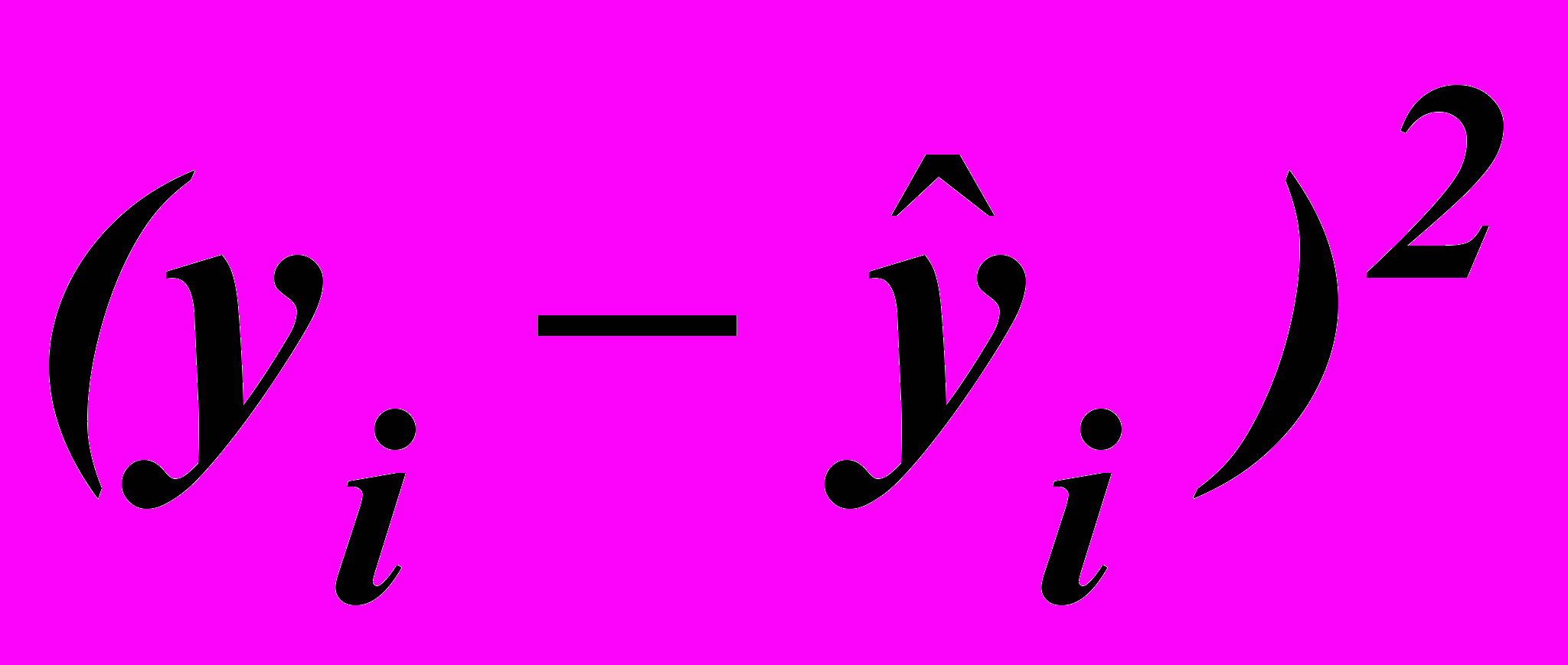 | 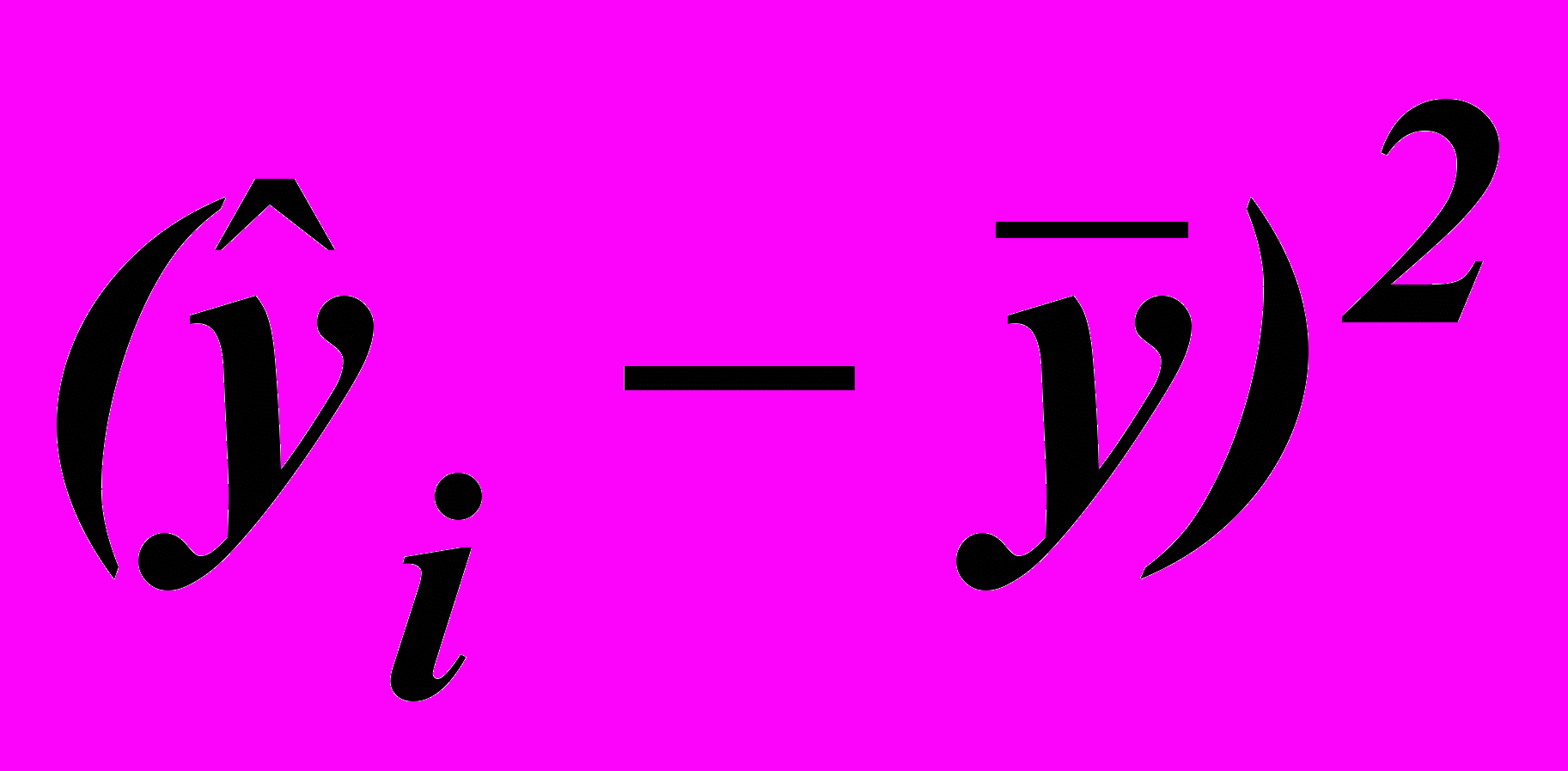 |
| 100 | 5,00 | 6,38125 | 5,2384 | 0,05684 | 1,30611 |
| 150 | 5,40 | 5,4511 | 0,00261 | 0,86527 | |
| 200 | 5,65 | 5,6637 | 0,00019 | 0,51488 | |
| 300 | 6,30 | 6,0890 | 0,04452 | 0,08541 | |
| 400 | 6,74 | 6,5143 | 0,05094 | 0,01770 | |
| 500 | 7,06 | 6,9396 | 0,01449 | 0,31175 | |
| 600 | 7,38 | 7,3649 | 0,00023 | 0,96757 | |
| 700 | 7,52 | 7,7902 | 0,07301 | 1,98514 | |
| | | | |  = == 0,24822 | 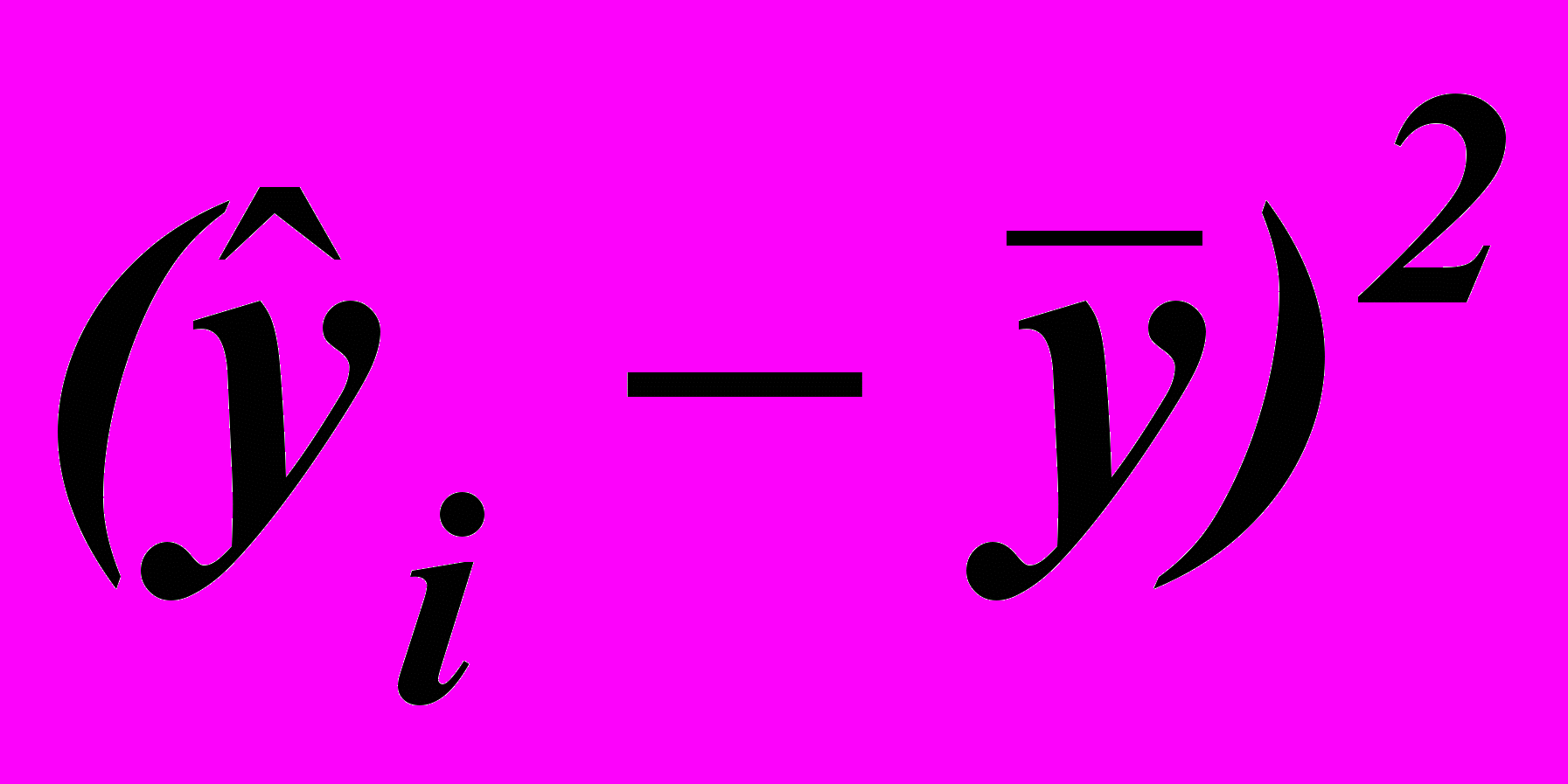 = == 6,05383 |
Обчислюємо величину F -критерію за формулою (6.27).
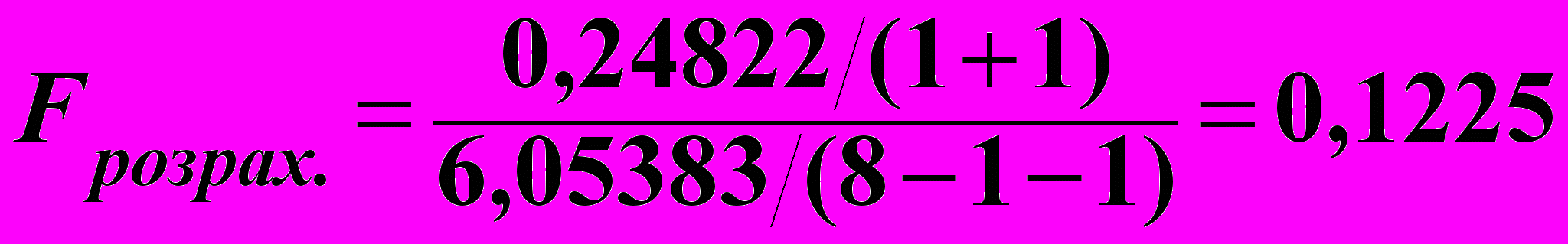 .
.При = 0,05; f1 = k + 1 = 2; f2 = n – k – 1 = 8 – 1 – 1 = 6;
k – кількість факторів.
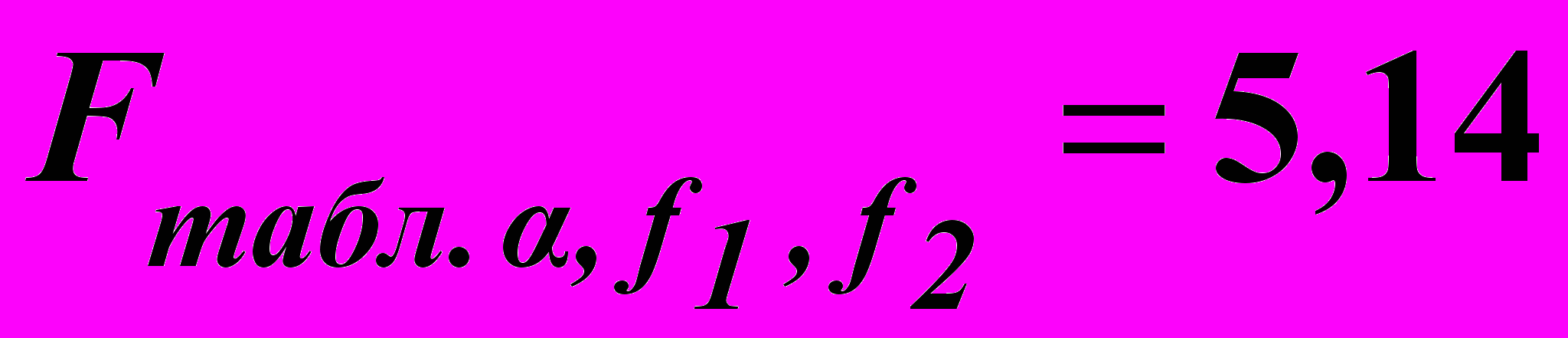 .
.Оскільки
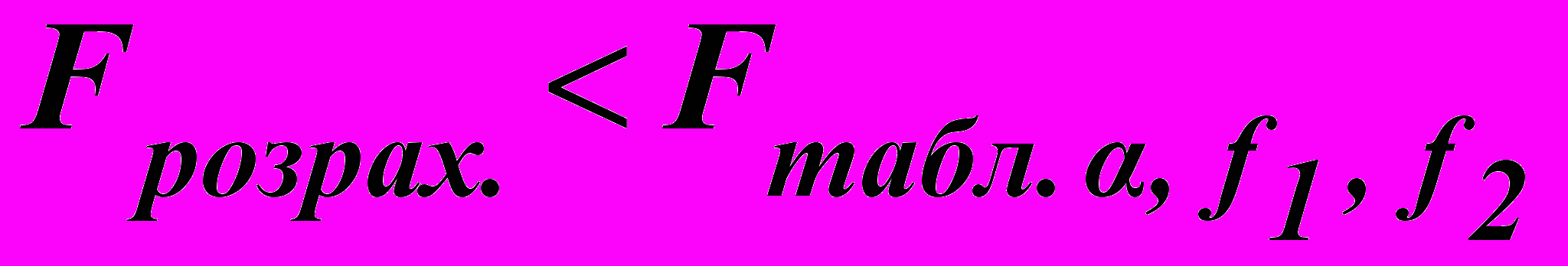 , робимо висновок, що рівняння регресії адекватне експериментальним даним і може бути математичною моделлю досліджуваної залежності густини пресовок з порошку міді від тиску пресування. Використовуючи цю модель, можна передбачити значення густини пресовок міді у разі зміни тиску пресування у досліджених межах, тобто від 100 до 700 МПа.
, робимо висновок, що рівняння регресії адекватне експериментальним даним і може бути математичною моделлю досліджуваної залежності густини пресовок з порошку міді від тиску пресування. Використовуючи цю модель, можна передбачити значення густини пресовок міді у разі зміни тиску пресування у досліджених межах, тобто від 100 до 700 МПа.Стандартна похибка передбачення значень густини пресовок за регресійною моделлю згідно з формулою (6.29) становитиме:
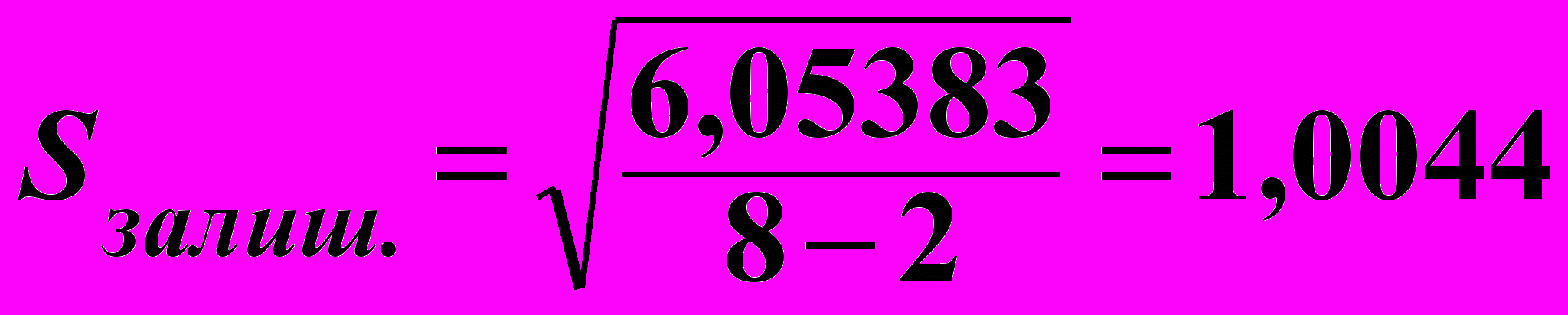 , г/см3.
, г/см3.Середня відносна похибка передбачення значень густини пресовок за регресійною моделлю згідно з формулою (6.30) становитиме:
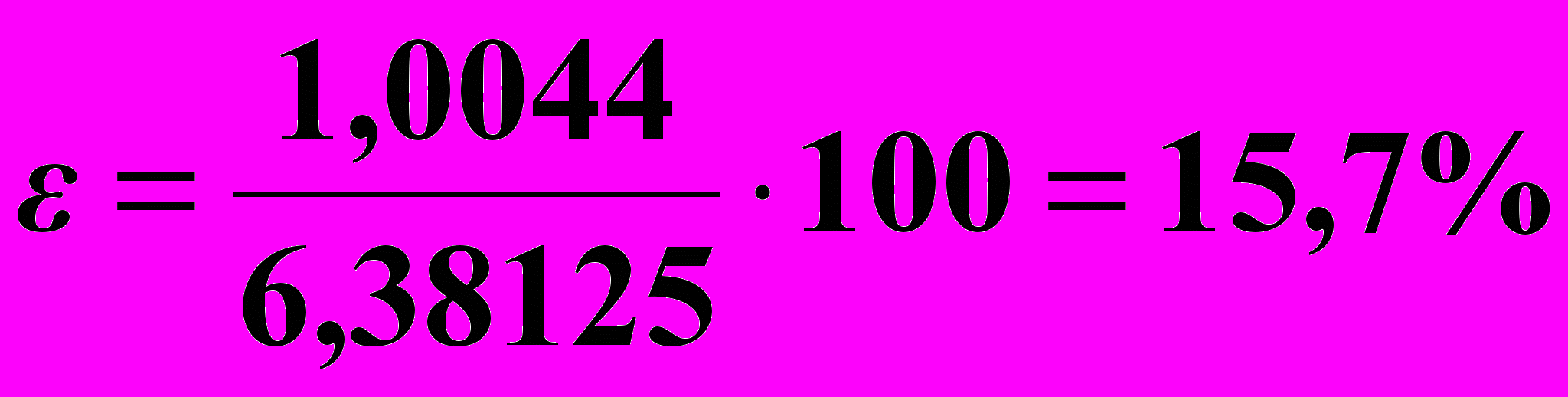 .
.Коефіцієнт детермінації згідно з формулою (6.24) становить: dyx = 0,982 100, тобто 96%.
Можна зробити висновок, що спостережувані експериментально зміни густини пресовок на 96% були зумовлені відповідними змінами тиску пресування.
Формули, що необхідні для виконання розрахункового завдання
Значення параметрів рівняння регресії знаходять за формулами:
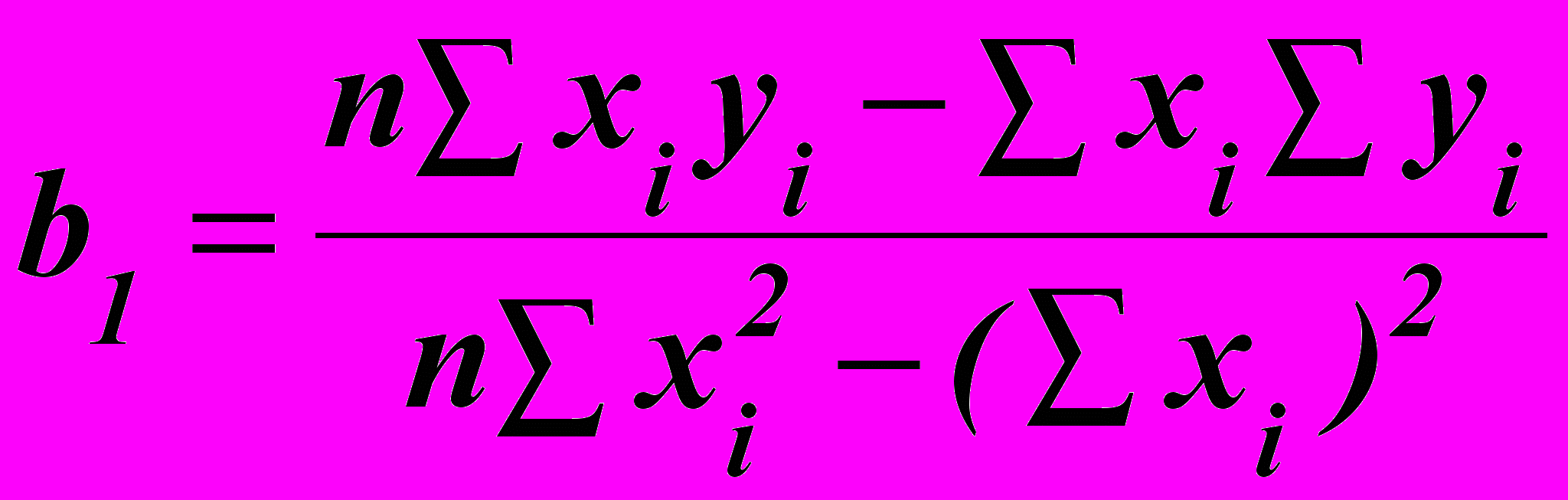 ; (6.8)
; (6.8)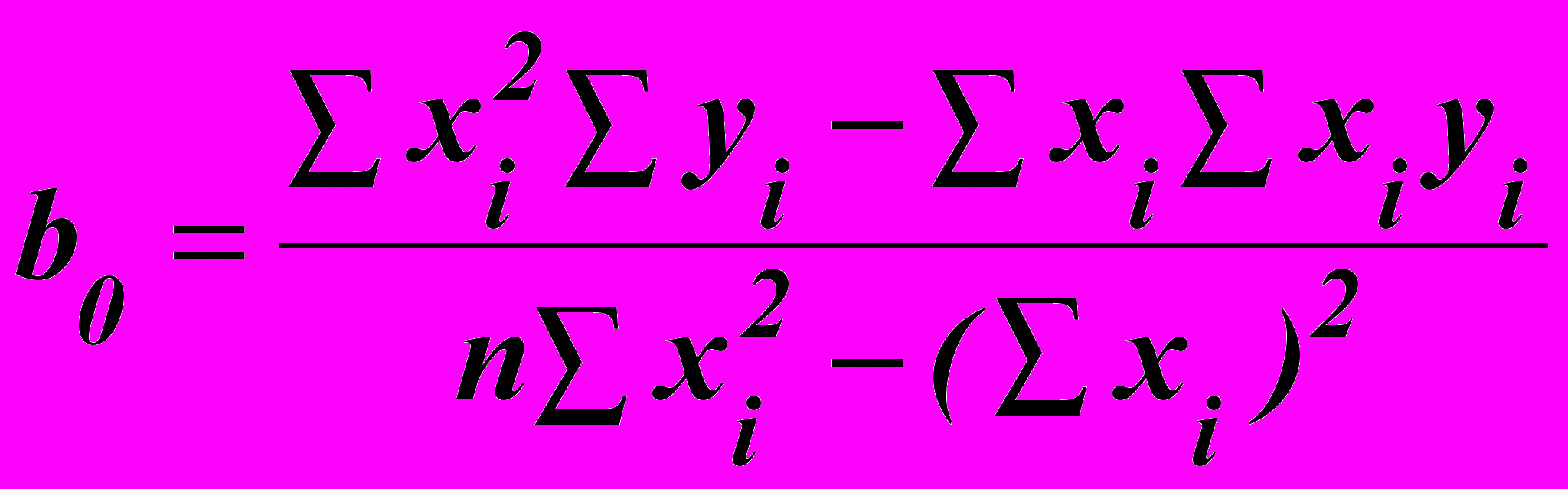 . (6.9)
. (6.9)Слід перевірити гіпотезу про статистичну значущість коефіцієнтів регресії, інакше кажучи, перевірити, чи суттєво їхня величина відрізняється від 0.
Оцінку статистичної значущості коефіцієнтів регресії роблять на основі t-критерію Стьюдента. Розрахункове значення t-критерію визначають для кожного коефіцієнта регресії з нерівності:
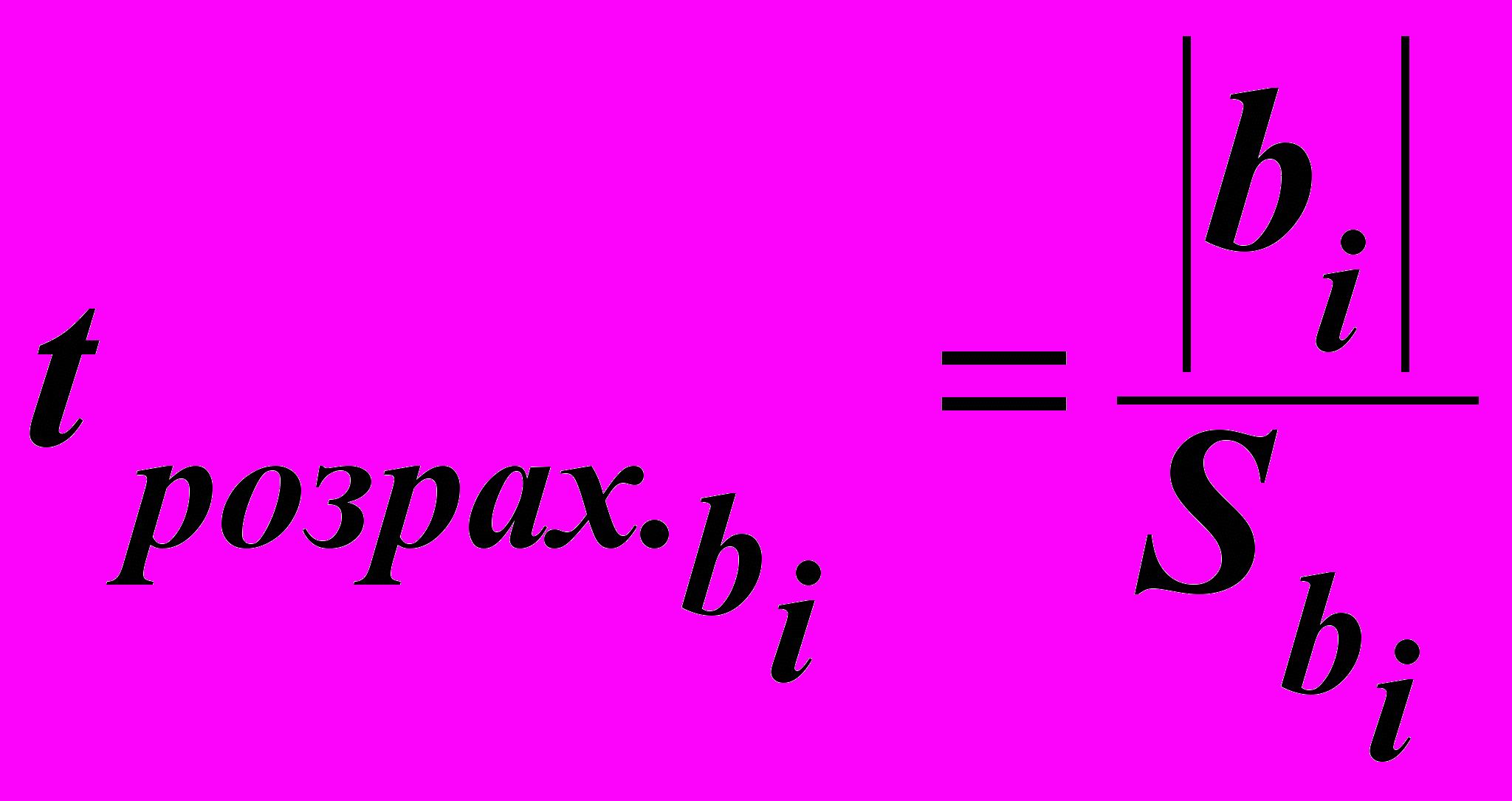 , (6.10)
, (6.10)де
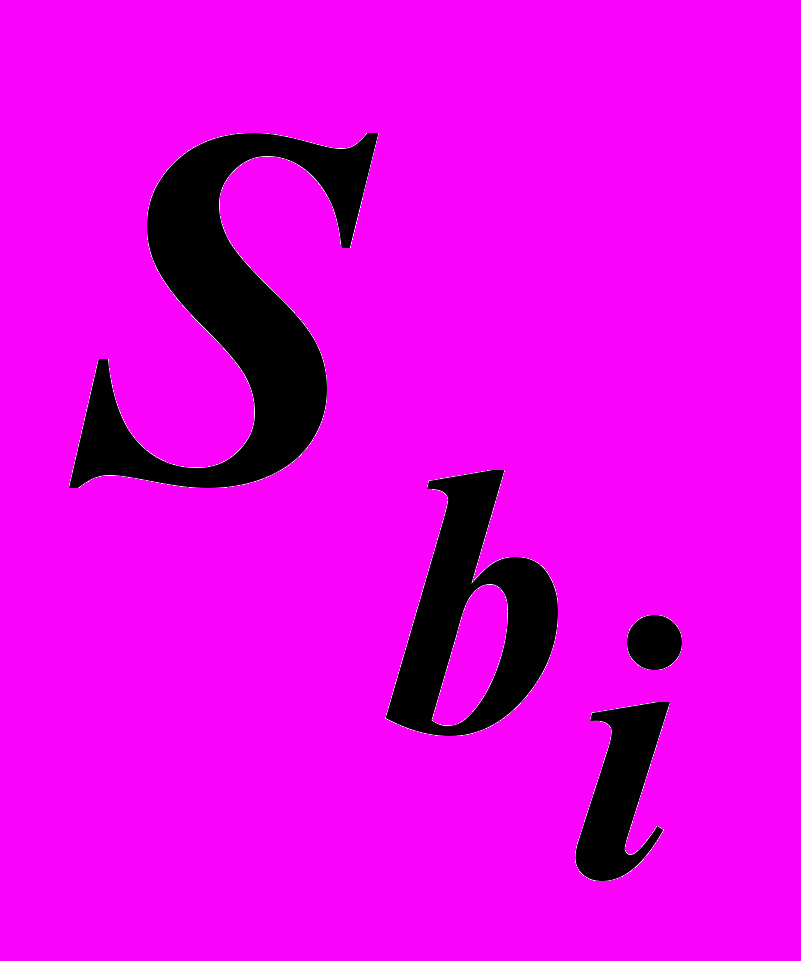 – стандартна похибка коефіцієнта bi, величина якої в загальному випадку може бути визначена за формулою:
– стандартна похибка коефіцієнта bi, величина якої в загальному випадку може бути визначена за формулою: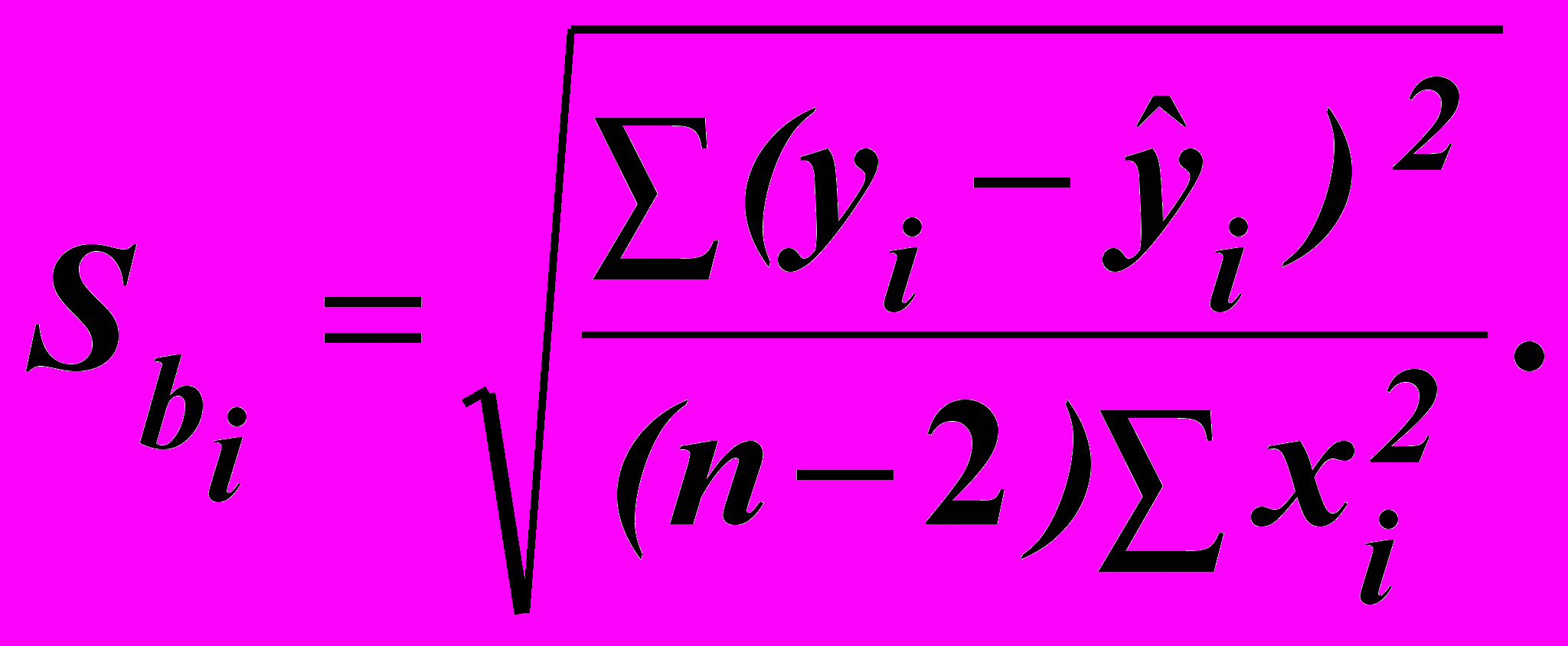 (6.11)
(6.11)Якщо виконується нерівність:
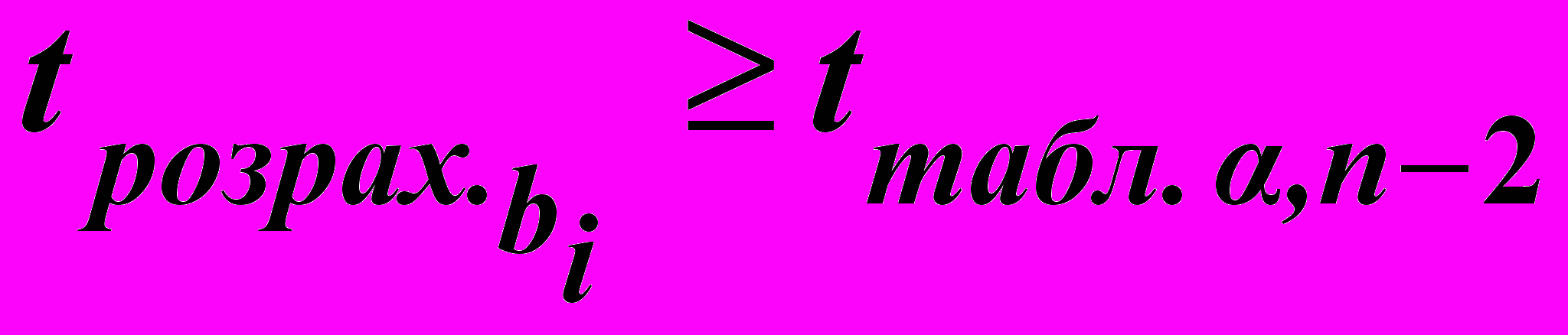 , (6.12)
, (6.12) то коефіцієнт регресії bi вважається статистично значущим для вибраного рівня значущості α. Якщо ж ця нерівність не виконується, то коефіцієнт bi вважається незначущим. Отже, відповідним доданком у рівнянні регресії можна знехтувати.
Коефіцієнт парної коpеляції ryx може бути визначений за однією за такою формулою:
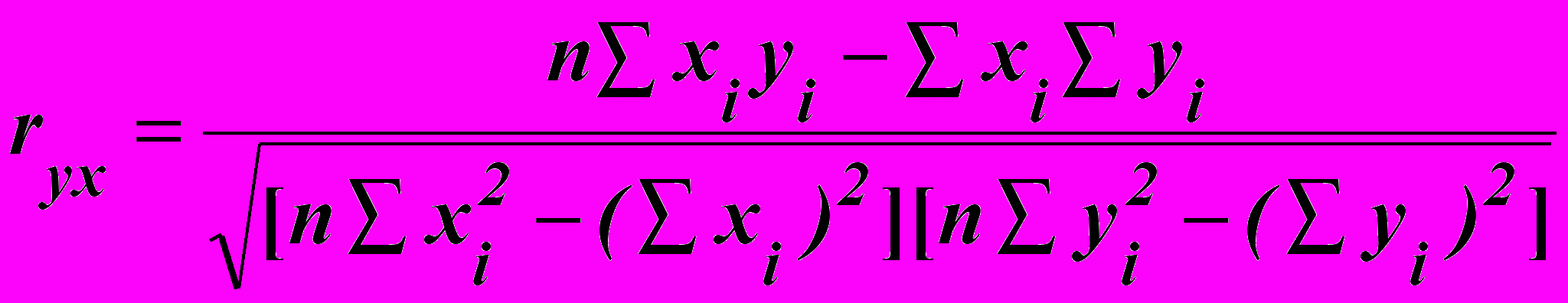 . (6.18)
. (6.18)Оцінювання адекватності рівняння регресії виконують за допомогою критерію Фішера, який визначається як відношення дисперсії, зумовленої регресією, тобто дисперсії адекватності:
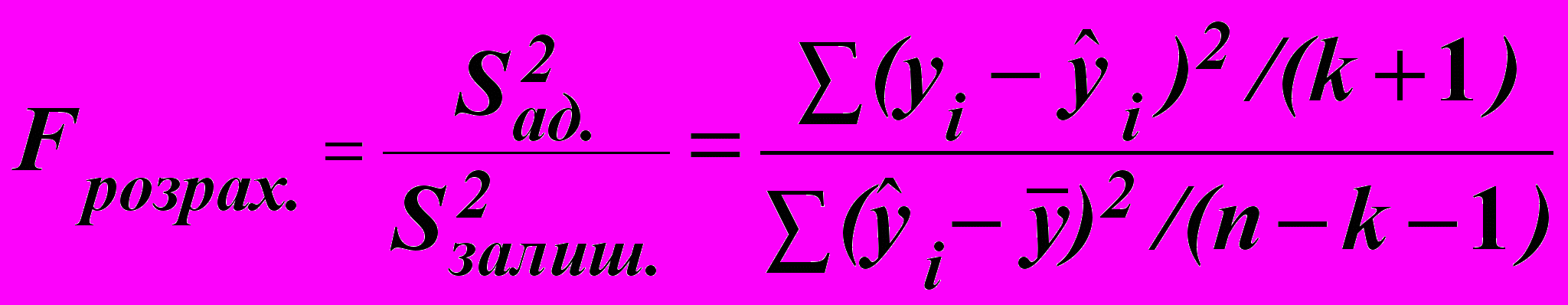 , (6.27)
, (6.27)де (k + 1) = f1 – число степенів свободи дисперсії адекватності;
(n – k – 1) = f2 – число степенів свободи залишкової дисперсії;
k – кількість факторів (у даному Вашому випадку – 1 фактор – тиск пресування, тобто k = 1).
У разі парної лінійної регресії f1 = 2; f2 = n – 2.
Розрахункове значення критерію Фішера Fрозрах. порівнюють з табличним за вибраного рівня значущості α. Якщо виконується нерівність
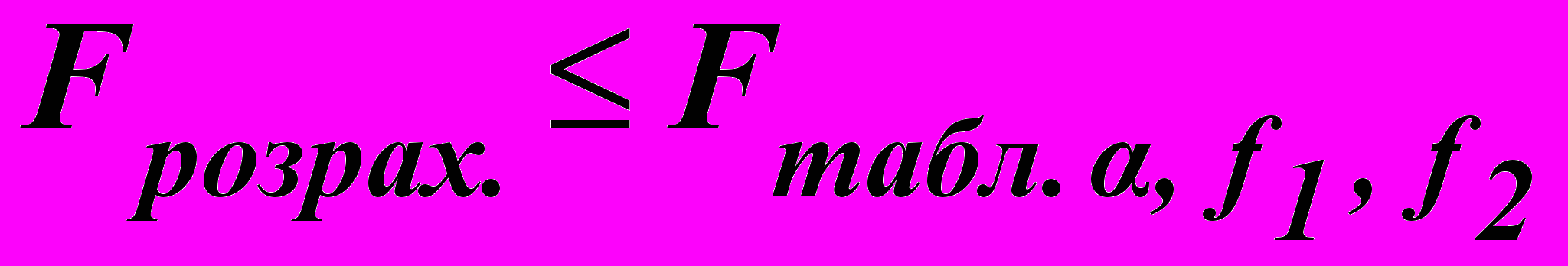 , (6.28)
, (6.28)то регресійна модель визнається адекватною і може бути використана для передбачення значень залежної змінної Y при всіх значеннях незалежної змінної Х у межах спостережуваних в експерименті значень останньої.
Визначають стандартну похибку апроксимації, тобто різницю
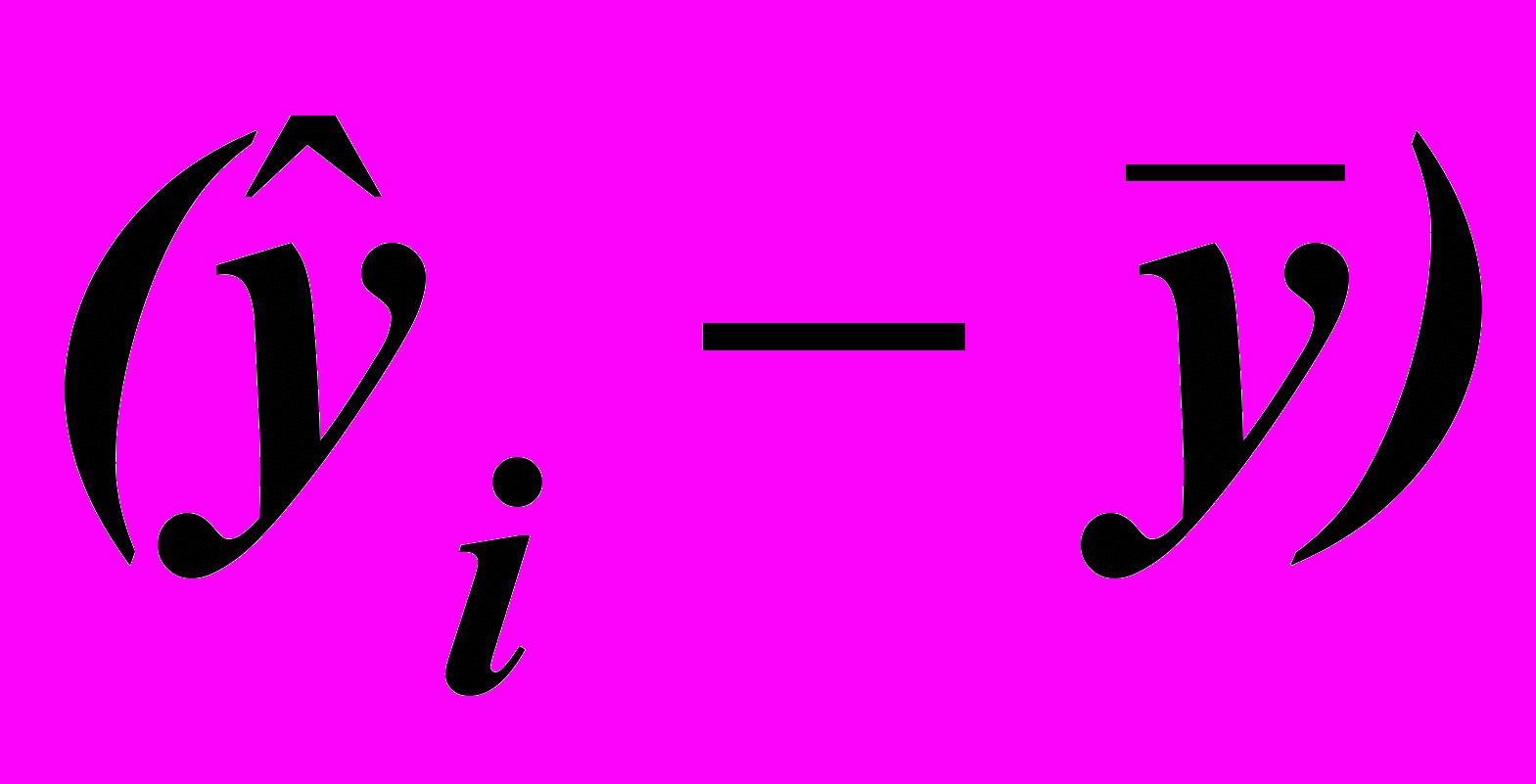 , яку можна використати для оцінки похибки передбачень залежної змінної Y за регресійною лінійною моделлю:
, яку можна використати для оцінки похибки передбачень залежної змінної Y за регресійною лінійною моделлю: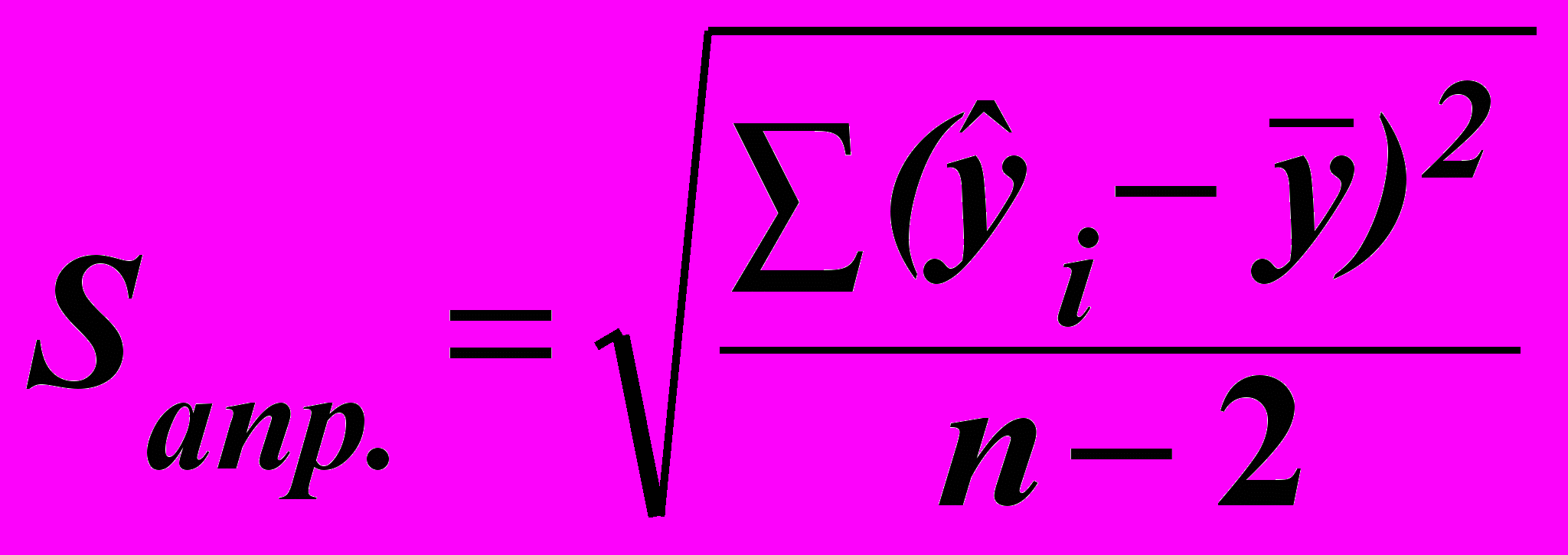 . (6.29)
. (6.29)Обчислюють також середню відносну похибку апроксимації (в % від середньої величини залежної змінної Y) за формулою:
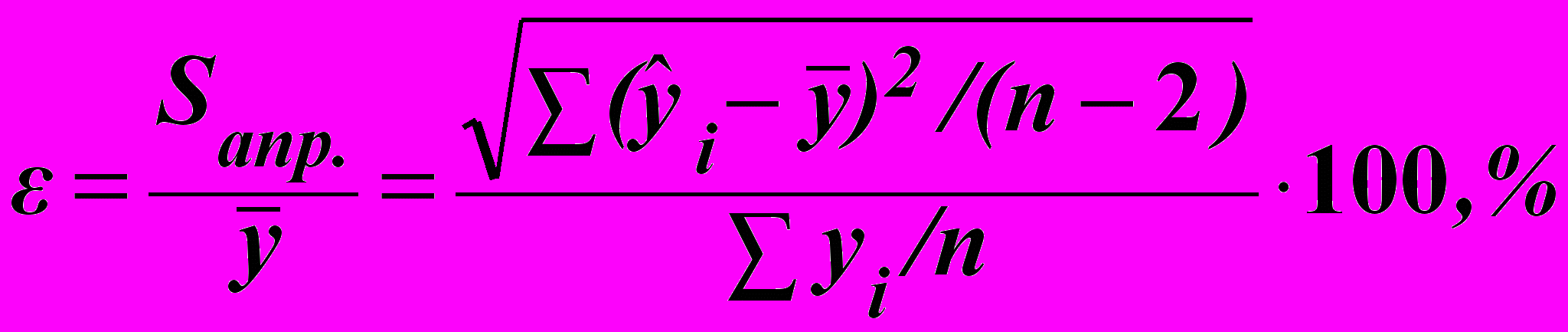 . (6.30)
. (6.30)Чим менша величина ε, тим точнішими будуть передбачення значень змінної Y за рівнянням регресії.
