О. О. Метешкін, д-р техн наук, проф. Харківського військового університету; > Н. А. Кизим, д-р екон. наук, проф. Харківського

Вид материала

Документы

Содержание СТАТИСТИЧНа Обробка ДАНИХ АПРОКСИМАЦІЯ та ІНТЕРПОЛЯЦІЯ Лінійна інтерполяція КУБІЧНА сплайн-інтерполяція Лінейне передбачення.

Подобный материал:

• А. В. Ковалевська Рецензенти: доцент, канд екон наук, доцент Харківського національного, 739.76kb.
• А. А. Гвоздев руководительтемы; доктора техн наук, 3579.39kb.
• Інформаційні технології в журналістиці: вітчизняний І світовий досвід Київ 2002, 8272.38kb.
• Дипломных проектов по специальностям, 283.96kb.
• Конкурс-захист проходив на базі Харківського національного університету ім. В. Н. Каразіна,, 342.15kb.
• «Сторінки історії Харківського університету за архівними документами», 72.28kb.
• Міжнародна журналістика – 2002 київ 2002, 2743.9kb.
• Приглашение и программа разнообразие почв и биоты северной и центральной азии, 521.14kb.
• Строительные нормы и правила бетонные и железобетонные конструкции, 3448.03kb.
• Надійності та безпеки в будівництві, 692.13kb.

СТАТИСТИЧНа Обробка ДАНИХ

• Апроксимація та інтерполяція;
  
• лінійна інтерполяція;
  
• кубічна сплайн-інтерполяція;
  
• інтерполяція функції двох змінних;
  
• регресія.
  

1. АПРОКСИМАЦІЯ та ІНТЕРПОЛЯЦІЯ

Дуже часто економічна інформація подається у вигляді набору деяких статистичних даних за певні періоди. Для аналізу цих даних часто виникає потреба визначити відсутні значення в проміжках між цими періодами або спрогнозувати розвиток подій на подальші періоди.

Для цих цілей статистичні дані варто апроксимувати, тобто побудувати деяку досить просту функцію, яка в зазначених точках буде приймати значення з наявного статистичного ряду. Тоді можна обчислити значення цієї функції між заданими точками (тобто зробити інтерполяцію даних) і за їх границями (екстраполяція).

MathCAD дозволяє провести апроксимацію даних за допомогою побудови лінійної функції і за допомогою кубічного полінома.

2. ЛІНІЙНА ІНТЕРПОЛЯЦІЯ

Лінійна інтерполяція дозволяє розрахувати проміжні значення за лінійною залежністю. Це означає з’єднання заданих точок ряду відрізками прямих. Для такої кусково-лінійної інтерполяції в MathCAD призначена функція linterp( ). Формат функції:


Linterp(vx,vy,x),


де vx, vy – вектори вихідних даних, причому дані мають бути упорядковані за зростанням, x – аргумент, для якого повертається значення y.

Приклад 1.

Є такі виробничі показники:

Кількість виробів	12	13	14	16	17	18	25	26	28
Витрата ресурсу	37	32	31	34	35	41	45	44	40

Потрібно провести лінійну інтерполяцію наявної залежності для того, щоб обчислити значення для х=15, х=20, х=30.

Розв’язання.



Тоді для побудованої функціональної залежності y(x) (кусково-лінійної) можна обчислити значення



Для цілей екстраполяції функція linterp( ) практично не призначена, тому значення в точці х = 30 обчислювати не будемо.

3. КУБІЧНА сплайн-інтерполяція

Лінійна інтерполяція дає досить грубе наближення (особливо для невеликого числа точок). У вузлових точках спостерігаються різкі перегини, за границями області визначення функція непередбачена.

MathCAD надає можливість апроксимувати вихідні дані іншим способом – відрізками кубічних поліномів, – так звана кубічна сплайн-інтерполяція.

Кубічна сплайн-інтерполяція дозволяє провести через набір точок гладку криву так, щоб у цих точках були неперервні перша й друга похідні. Інтерполяція здійснюється у два етапи:

• спочатку обчислюється вектор других похідних vs у точках, що розглядаються;
  
• потім обчислюється значення функції в точці x за допомогою функції interp(vs,vx,vy,x).
  

Для обчислення вектора других похідних vs у MathCAD існує цілих три функції. Вони відрізняються одна від одної тільки граничними умовами:

cspline(vx,vy) наближає криву у вузлових точках до кубічного поліному;

pspline(vx,vy) наближає криву в опорних точках до параболи;

lspline(vx,vy) наближає криву в заданих точках до прямої.

Приклад 2. Інтерполюємо ті ж вихідні дані за допомогою кубічної сплайн-інтерполяції. Скористаємося для першого етапу функцією cspline(vx,vy):



Обчисліть другі похідні двома способами, що залишилися. Побудуйте для всіх трьох способів розрахунку вектора vs графіки відповідної кубічної сплайн-інтерполяції. Порівняйте візуально відмінності всіх трьох графіків.





Порівняйте також значення в точках х=15, 20, 30 для всіх трьох функцій, що утворилися:





Інтерполяція вектора точок.

Ми могли б побудувати інтерполяційну таблицю з однаковим кроком, використовуючи оператор векторизації. Наприклад, для розглянутої задачі нам потрібно укласти таблицю значень функції на інтервалі від 5 до 6.




Лінейне передбачення.

У MathCAD є функція predict(v, m, n), яка дозволяє зробити передбачення поведінки функції поза інтервалом її задання. Ця функція використовує лінійний алгоритм передбачення. Тут v – вектор даних, m – кількість послідовних точок вихідного вектора, що використовуються для передбачення (усі точки задані з однаковим кроком), n – кількість передбачуваних точок.

Подивимося, як за допомогою цієї функції можна передбачити значення для розглянутої задачі.










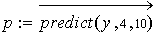
Функція використовує останні m точок, щоб обчислити коефіцієнти передбачення, після чого обчислює координати n точок вперед.