О. О. Метешкін, д-р техн наук, проф. Харківського військового університету; > Н. А. Кизим, д-р екон. наук, проф. Харківського

Вид материала

Документы

Содержание Числове диференціювання Символьне ДИФЕРЕНЦІЮВАННЯ Символіка / Обчислення / Символьно Символіка / Змінна / Диференціювати. ДИФЕРЕНЦІЮВАННЯ В частинних ПОХІДНИХ ЗАСТОСУВАННЯ похідних ПРИ Розв’язаннІ ЕКОНОМІЧНИХ ЗАДАЧ Розрахунок продуктивності праці Аналіз виробничих функцій К(х) – функція, що встановлює залежність витрат виробництва від кількості х U(x) – виторг від продажів х Питання для самоконтролю Практична робота № 5

Подобный материал:

• А. В. Ковалевська Рецензенти: доцент, канд екон наук, доцент Харківського національного, 739.76kb.
• А. А. Гвоздев руководительтемы; доктора техн наук, 3579.39kb.
• Інформаційні технології в журналістиці: вітчизняний І світовий досвід Київ 2002, 8272.38kb.
• Дипломных проектов по специальностям, 283.96kb.
• Конкурс-захист проходив на базі Харківського національного університету ім. В. Н. Каразіна,, 342.15kb.
• «Сторінки історії Харківського університету за архівними документами», 72.28kb.
• Міжнародна журналістика – 2002 київ 2002, 2743.9kb.
• Приглашение и программа разнообразие почв и биоты северной и центральной азии, 521.14kb.
• Строительные нормы и правила бетонные и железобетонные конструкции, 3448.03kb.
• Надійності та безпеки в будівництві, 692.13kb.

ДИФЕРЕНЦІЮВАННЯ

• Похідна;
  
• числове й символьне диференціювання;
  
• застосування похідних при розрахунку продуктивності праці, граничних витрат виробництва, еластичності, при аналізі виробничих функцій.
  

1. ДИФЕРЕНЦІЮВАННЯ

Для обчислення похідної достатньо поставити функцію під знак

Цей знак уводиться або з панелі математичного аналізу, або за допомогою клавіші ? (англ. мовою).

2. ЧИСЛОВЕ ДИФЕРЕНЦІЮВАННЯ

Для числового диференціювання:

• спочатку присвойте значення аргументу;
  
• потім уставте знак похідної та функцію, що диференціюється, й натисніть =.
  

3. Символьне ДИФЕРЕНЦІЮВАННЯ

Для символьного диференціювання можна запропонувати декілька способів:

А) уставити знак диференціювання та вираз, що диференціюється, і натиснути знак символьної рівності  (або з панелі інструментів Символіка, або за допомогою клавіатури: Ctrl+.);

Б) уставити знак диференціювання і вираз, що диференціюється, виділити увесь вираз (синім кутком) і вибрати меню Символіка / Обчислення / Символьно (або комбінацію клавіш Shift+F9);

В) надрукувати лише вираз, що диференціюється, виділити змінну, за якою диференціюємо, і вибрати меню Символіка / Змінна / Диференціювати.




Перший спосіб відрізняється від двох наступних тим, що вони вразливі до присвоєння значення змінній, що диференціюється. Якщо перед диференціюванням визначити значення змінної, то отримаємо числове значення похідної:



Цього ж результату можна досягти, використовуючи звичайний знак рівності:



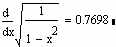
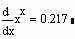Перевіримо: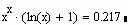


Другий і третій способи видають похідну в символьному вигляді, навіть якщо перед цим змінній, що диференціюється, було присвоєне значення. Наприклад, присвоїмо х:=10 і викличемо команду Символіка / Обчислення / Символьно для виділеного виразу :




Приклад. Обчислити значення похідної третього порядку функції y(x)=sin⁵ x + ln x у точках х=3 та х=10. Побудувати графіки функції та її третьої похідної.

4. ДИФЕРЕНЦІЮВАННЯ В частинних ПОХІДНИХ

Аналогічно здійснюється диференціювання в частинних похідних. Для цього слід в знаку диференціювання зазначити ту зі змінних, за якою диференціюємо:

5. ЗАСТОСУВАННЯ похідних ПРИ Розв’язаннІ ЕКОНОМІЧНИХ ЗАДАЧ

Поняття похідної дуже широко застосовується в економічних розрахунках та задачах. Так, похідна дозволяє визначити продуктивність праці, проаналізувати різні виробничі функції або визначити еластичність чинників при аналізі функцій попиту та споживання. Крім того, за допомогою диференціювання розв’язується величезний клас оптимізаційних задач.

РОЗРАХУНОК ПРОДУКТИВНОСТІ ПРАЦІ

Нехай функція виражає кількість зробленої продукції за час . Потрібно знайти продуктивність праці в момент часу t₀.

За відрізок часу від t₀ до кількість зробленої продукції зміниться від значення до значення . Тоді середня продуктивність праці за цей час буде дорівнювати .

Продуктивність праці в момент часу визначається граничним значенням середньої продуктивності праці за проміжок часу від до при , тобто: .

Таким чином, продуктивність праці в момент – це похідна обсягу виробленої продукції за часом у цей момент t₀.

АНАЛІЗ ВИРОБНИЧИХ ФУНКЦІЙ

Виробничою функцією називається аналітичне співвідношення, що пов’язує змінні величини витрат (чинників, ресурсів) із величиною випуску продукції (виторгу, витрат виробництва та ін.). Ці функції використовуються для встановлення залежностей виторгу від продажу товару, випуску продукції від витрат ресурсів, витрат виробництва від обсягу продукції тощо. Їх диференціальні характеристики пов’язані із поняттям похідної.

Якщо К(х) – функція, що встановлює залежність витрат виробництва від кількості х продукції, що випускається, то границя



називається граничними витратами виробництва. Величина характеризує (приблизно) додаткові витрати на виробництво одиниці додаткової продукції.

Якщо U(x) – виторг від продажів х одиниць товару, то границя



називається граничним виторгом.

Якщо виробнича функція y=f(x) установлює залежність випуску продукції y від витрат ресурсу x, то границя



називається граничним продуктом.

ЕЛАСТИЧНІСТЬ

У багатьох задачах зручніше обчислювати відсоток (відносний приріст) від приросту залежної змінної, відповідний відсотку приросту незалежної змінної. Це приводить до поняття еластичності функції, яку іноді називають відносною похідною.

Еластичністю функції відносно змінної х називається границя відношення відносного приросту цієї функції до відносного приросту змінної х при :





Еластичність звичайно позначається Е_x(y).

Таким чином, еластичність відносно х є наближений процентний приріст функції (підвищення або зниження), що відповідає приросту незалежної змінної на 1%.




Основні властивості еластичності функції

1. Еластичність функції дорівнює добутку незалежної змінної х на темп зміни функції , тобто: .
   
2. Еластичність добутку (або частки) двох функцій дорівнює сумі (різниці) еластичності цих функцій:
   

,

.

3. Якщо , то: .
   

Еластичність функції застосовується при аналізі попиту і споживання. Наприклад, еластичність попиту відносно ціни х (або прибутку) – коефіцієнт, що показує приблизно, на скільки відсотків зміниться попит (обсяг споживання) при зміні ціни (або прибутку) на 1%.

Якщо еластичність попиту за абсолютною величиною більша за одиницю, то попит вважається еластичним, якщо дорівнює одиниці – нейтральним, якщо менший за одиницю – нееластичним щодо ціни (або прибутку).

Високий коефіцієнт еластичності означає слабкий ступінь задоволення потреби; низький – велику потребу в даному товарі.

ПИТАННЯ ДЛЯ САМОКОНТРОЛЮ

1. Які можливості диференціювання є в MathCAD?
   
2. Як організувати числове диференціювання виразу?
   
3. Які способи символьного диференціювання в MathCAD Ви знаєте?
   
4. У чому відмінність символьного диференціювання за допомогою меню Символіка і за допомогою знака символьної рівності?
   
5. Як обчислити похідну другого, третього й більш високих порядків?
   
6. Як розрахувати часткову похідну?
   
7. Які Ви знаєте економічні задачі, що вимагають для свого розв’язання узяття похідних?
   
8. Як розраховується еластичність функції?
   
9. Які властивості еластичності функції?
   
10. Що таке граничні витрати, граничний продукт? Як вони розраховуються?
    

ПРАКТИЧНА РОБОТА № 5

Завдання 1.

Нехай функція K(x)=20x–x²/20 встановлює залежність витрат виробництва від кількості х продукції, що випускається. Знайти граничні витрати виробництва й коефіцієнт еластичності, якщо обсяг продукції становить 100 одиниць, 20 одиниць. Побудувати графіки виробничої функції, її еластичності та граничних витрат виробництва.

Розв’язання.

1. Графік виробничої функції:
   

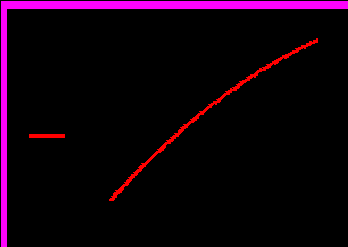
2. Граничні витрати виробництва: K′ (x) =
   

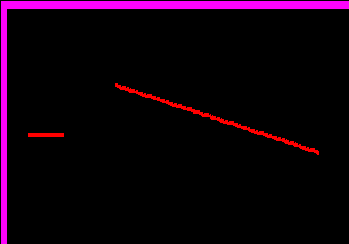
За x = 100 та x = 20 – граничні витрати виробництва відповідно дорівнюють 10 та 18.

Чим більше виробляється продукції, тим повільніше зростають витрати на її випуск.

3. Еластичність функції дорівнює:
   

Графік еластичності:




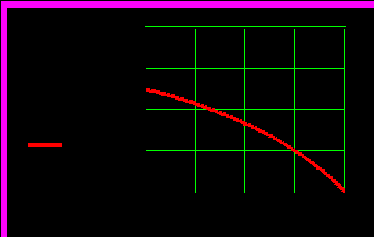
При х = 100 – еластичність функції дорівнює:

При х = 20 – еластичність функції дорівнює: :

Відповідь: при обсязі випуску в 100 одиниць, якщо кількість продукції, що випускається, збільшиться на 1%, тобто на одиницю, то відносні витрати виробництва збільшаться на 0,67%; при обсязі в 20 одиниць збільшення випуску продукції на 1% спричинить збільшення відносних витрат приблизно на 0,95%.


Завдання 2.

Побудувати графік та ізокванти виробничої функції, яка задає залежність результатів виробництва від двох факторних показників – праці й капіталу: 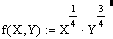. Обчислити граничні продукти праці й капіталу, а також коефіцієнт замінності ресурсів.


Розв’язання.

1. Графік виробничої функції:
   

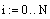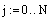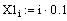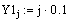2. Для побудови графіка ізоквант (або виробничих кривих байдужості – ліній, що відповідають однаковому випуску продукції) виберіть при побудові графіка в MathCAD меню Вставка / Графік / Контурний графік:
   

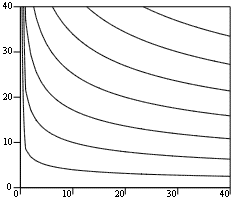
3. Обчислимо граничний продукт праці:
   

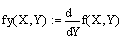
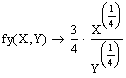
4. Обчислимо граничний продукт капіталу:
   

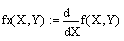
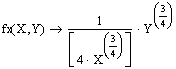
5. Обчислимо коефіцієнт замінності ресурсів:
   

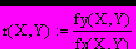
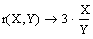
Завдання 3.

Фірма виробляє два види товарів і продає їх за ціною 1000 грош. од. і 800 грош. од. відповідно. Обсяги випуску товарів – Q₁ и Q₂. Функція витрат має вигляд C(Q₁,Q₂) = 2Q₁²+2Q₁Q₂+Q₂². Потрібно визначити, за яких обсягів випуску товару прибуток буде максимальним. Знайти цей прибуток. Побудувати графік залежності прибутку від обсягів випуску.

Розв’язання.

1. Сумарний доход від продажу товарів: R(Q₁,Q₂) = 1000Q₁+800Q₂. Тоді прибуток (різниця між доходом і витратами):

P(Q₁,Q₂) = R(Q₁,Q₂) – C(Q₁,Q₂).

.

1. Для пошуку максимуму прибутку P(Q₁,Q₂) визначимо стаціонарні точки (у яких часткові похідні дорівнюють нулю):
   

Прирівнявши ці похідні до нуля, одержуємо систему рівнянь:




Таким чином, стаціонарна точка М₀(100; 300).

2. Перевіримо, чи є дана точка точкою максимуму. Для цього знаходимо часткові похідні другого порядку.
   
3. Прибуток при обсягах випуску товарів 100 і 300 відповідно буде дорівнювати (грош. од.).
   
4. Побудуємо графік залежності прибутку від обсягів випуску: