О. О. Метешкін, д-р техн наук, проф. Харківського військового університету; > Н. А. Кизим, д-р екон. наук, проф. Харківського

Вид материала

Документы

Содержание Задачі оптимізації ПОШУК екстремумів ФУНКЦІЙ ЗАДАЧі ЛІНІЙНОГО, НЕЛІНІЙНОГО, цілочислового ПРОГРАМУВАННЯ Питання для самоконтролю Практична робота № 6 Задача 3А. Задача 3Б. Пошук розв’язку Задача 4Б.

Подобный материал:

• А. В. Ковалевська Рецензенти: доцент, канд екон наук, доцент Харківського національного, 739.76kb.
• А. А. Гвоздев руководительтемы; доктора техн наук, 3579.39kb.
• Інформаційні технології в журналістиці: вітчизняний І світовий досвід Київ 2002, 8272.38kb.
• Дипломных проектов по специальностям, 283.96kb.
• Конкурс-захист проходив на базі Харківського національного університету ім. В. Н. Каразіна,, 342.15kb.
• «Сторінки історії Харківського університету за архівними документами», 72.28kb.
• Міжнародна журналістика – 2002 київ 2002, 2743.9kb.
• Приглашение и программа разнообразие почв и биоты северной и центральной азии, 521.14kb.
• Строительные нормы и правила бетонные и железобетонные конструкции, 3448.03kb.
• Надійності та безпеки в будівництві, 692.13kb.

ЗАДАЧІ ОПТИМІЗАЦІЇ

• Задачі оптимізації;
  
• функції maximize( ) й minimize( );
  
• лінійне програмування (ЛП);
  
• задача оптимального завантаження виробничих потужностей;
  
• транспортна задача (відкрита, закрита);
  
• цілочислове програмування;
  
• задача про комівояжера;
  
• нелінійне програмування (НЛП).
  

1. ПОШУК екстремумів ФУНКЦІЙ

Термін оптимізація має дуже широкий ужиток, а тому може залежати від контексту. Будемо розуміти оптимізацію як процес знаходження екстремуму (максимального або мінімального значення) економічних функцій, тобто вибір найкращого варіанта з можливих.

У MathCAD існують дві функції спеціально для пошуку максимумів і мінімумів – maximize( ) та minimize( ). Перед використанням цих функцій треба присвоїти початкове значення (наближення) аргументу функції, що оптимізується. Загальний вигляд функцій: maximize (f, x₁, x₂,…), де f – назва функції f(x₁, x₂,…), що максимізується, а x₁, x₂, … – аргументи, за якими шукається максимум (аналогічно для мінімуму).

Якщо в задачі є обмеження, то їх треба зазначити перед викликом цих функцій, попередивши їх ключовим словом given.

Можливість запису перед функціями maximize( ) та minimize( ) системи обмежень у вигляді нерівностей і рівностей дозволяє розв’язувати в середовищі MathCAD широкий клас оптимізаційних задач під назвою задачі лінійного програмування.

2. ЗАДАЧі ЛІНІЙНОГО, НЕЛІНІЙНОГО, цілочислового ПРОГРАМУВАННЯ

Задача лінійного програмування (ЛП) у загальному вигляді формулюється в такий спосіб:

потрібно знайти екстремум (мінімум або максимум) цільової функції



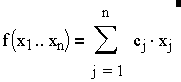
за обмежень:



,

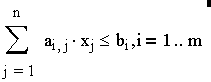
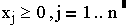де c_j – витрати або прибуток (у випадку мінімізації або максимізації відповідно);

a_ij – питомі витрати i-го ресурсу на одиницю випуску j-го продукту;

b_i – ліміти ресурсів або кількісне вираження попиту;

(a_ij, b_i, c_j – задані числові значення)

x_j – шукані кількості j-го продукту;

f(x₁,…, x_n) називається цільовою функцією.

Обмеження говорять про таке: у випадку мінімізаційної задачі (за обмеженості ресурсів) витрата ресурсів не може перевищувати їх наявність; у випадку максимізаційної задачі: потреби (попит) повинні бути цілком задоволені або перевищені.

У тому випадку, якщо обмеження задачі записані у вигляді рівностей (рівнянь), задача називається канонічною.

До задач ЛП відносяться задачі планування виробництва (задачі про використання ресурсів), задачі про суміші (про упорядкування раціону), про використання потужностей (про завантаження устаткування) тощо.

Однією із задач ЛП, що часто зустрічаються, є задача з розробки раціонального плану транспортних перевезень – так звана транспортна задача. Метою організації перевезень при цьому зазвичай є мінімізація витрат.

У загальному вигляді транспортна задача формулюється таким чином: потрібно перевезти певну кількість деяких вантажів із m пунктів відправлення до n пунктів призначення. При цьому необхідно мінімізувати сукупні витрати на транспортування всіх партій вантажу:



Обмеження



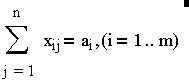
описують вимоги того, що весь вантаж має бути вивезений, а обмеження:



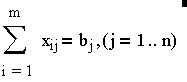
вимоги того, що має бути задоволена потреба у вантажах в кожному пункті призначення. Крім того, кількість перевезеного вантажу не може бути від’ємною:



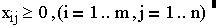
де c_ij – витрати на транспортування одиниці вантажу з і-го пункту відправлення до j-го пункту призначення;

a_i – загальна кількість вантажу в i-му пункті відправлення;

b_j – загальна потреба у вантажі в j-му пункті призначення;

x_ij – кількість вантажу, перевезеного з i-го пункту відправлення до

j -го пункту призначення (невідомі величини, які треба знайти).

Якщо виконується умова:

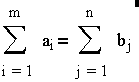(сумарна наявність вантажу збігається із сумарною потребою), то транспортна задача називається закритою. Інакше транспортна задача – відкрита. Розв’язання відкритої транспортної задачі в математиці зазвичай зводиться до розв’язання закритої задачі шляхом уведення ще одного (фіктивного) пункту призначення або споживання, який бере на себе різницю між наявністю вантажу й потребою. Однак для Excel або MathCAD відкритість або закритість задачі не є принциповим моментом.

Ще одна типова задача ЛП – задача оптимального завантаження виробничих потужностей. Постановка цієї задачі залежить від того, взаємозамінні чи ні розглянуті групи устаткування.

Якщо групи устаткування не взаємозамінні, то задаються а_ij – коефіцієнти витрат часу на обробку на i-му устаткуванні j-х виробів (деталей, вузлів), А_i – фонд часу по кожній групі устаткування у верстато- або машино-годинах, с_j – ефективність виробництва j-го виробу, а також часто зазначаються мінімально необхідні потреби в j-х виробах (В_mj) та верхні обмеження випуску (B_Mj), обумовлювані лімітами на матеріали. Шукане число виробів, оброблюваних на устаткуванні, приймається за x_j.

Тоді модель ЛП для невзаємозамінних груп устаткування буде мати вигляд:



, j=1,…,m

B_mj≤x_j≤B_Mj, j=1,…,m


Різновидом задачі ЛП є цілочислова задача, у якій всі елементи x_i – цілі числа. Класичним прикладом цілочислової задачі є задача про комівояжера (задача про призначення, про розподіл замовлень, розстановку персоналу тощо). Задачу про комівояжера можна застосувати при визначенні оптимальної послідовності обробки деталей, розвезення товарів, підведення електроенергії до робочих місць тощо.

Для розв’язання задачі про комівояжера за невідомі приймаються змінні x_ij, рівні або 1 (i-а деталь оброблюється на j-му верстаті), або 0 (не оброблюється). У матриці, складеній з таких змінних x_ij, у кожному рядку й у кожному стовпці має міститися рівно по одній одиниці.

На жаль, MathCAD не вміє розв’язувати задачі цілочислового програмування. Однак, як у Excel, до нього можна підключити пакет аналізу Solving and Optimization Extension Pack (Expert Solver), який надасть цю й багато інших додаткових можливостей розв’язання оптимізаційних задач.

Задачі лінійного програмування (ЛП) – окремий випадок задач нелінійного програмування (НЛП). В останніх і цільова функція, й обмеження можуть бути нелінійними функціями. Узагальнено задача НЛП має вигляд:

F(x₁,…, x_n)  max(min);

g_i(x₁,…, x_n)≤b_i, i=1,…,m;

x_j≥0, j=1,…,n.

ПИТАННЯ ДЛЯ САМОКОНТРОЛЮ

1. Яким чином у математичному аналізі функцій організований пошук екстремумів (максимумів, мінімумів)? Яку роль при цьому відіграють перша й друга похідні?
   
2. Які функції в MathCAD призначені спеціально для пошуку мінімумів і максимумів?
   
3. У чому відмінність задач лінійного й нелінійного програмування?
   
4. Запишіть загальний вигляд задачі лінійного програмування.
   
5. Які принципові характеристики задач цілочислового програмування?
   
6. Як роз’вязувати в MathCAD задачі цілочислового програмування?
   
7. Що таке задача про комівояжера? Сформулюйте її.
   
8. Сформулюйте умови й вимоги транспортної задачі.
   
9. Що значить відкрита (закрита) транспортна задача?
   
10. Сформулюйте умови й вимоги задачі оптимального завантаження виробничих потужностей.
    
11. Запишіть загальний вигляд задачі нелінійного програмування.
    
12. Які засоби Excel для розв’язання задач оптимізації Вам відомі?
    

ПРАКТИЧНА РОБОТА № 6

Задача 1.

Припустімо, що виробнича функція залежить тільки від чисельності персоналу фірми (так звана однофакторна модель виробництва) і має вигляд Q(L) = 20L² – 0,2L³, де Q – кількість продукції, що випускається, а L – число працівників. Потрібно визначити чисельність персоналу, при якій випуск Q досягає максимального значення.

Побудуйте графік функції. Урахуйте, що графік функції необхідно будувати не для всіх значень L від – до + (подумайте, які обмеження треба врахувати?). Визначити за графіком кількість екстремальних точок та їх тип (min, max).

Розв’язання 1.

1. Для знаходження L, при якому досягається екстремум, знайдіть похідну функції й дорівняйте її до 0 (виконайте символьне розв’язання). Вийде рівняння, коренем якого буде значення L.
   
2. Для розв’язання такого рівняння скористайтеся функцією polyroots (або root). Як визначити, максимальний чи мінімальний випуск продукції при цьому значенні L? (наприклад, знайдіть значення другої похідної функції при цьому значенні L і переконайтеся в її від’ємності).
   

Розв’язання 2.

Розв’язати ту ж задачу за допомогою функції maximize. Не забудьте обмеження на додатність аргументу.

Чи відрізняються результати розв’язання, отримані 1 і 2 способами?

Розв’язання 3.

MathCAD не вміє розв’язувати цілочислові задачі. От і в цих двох випадках: яке значення є розв’язком – 66 чи 67 осіб?

Розв’язати цю задачу (цілочислово) в Excel за допомогою механізму пошуку розв’язку. Чи збігається результат із результатом MathCAD?


Задача 2. Задача про оптимальний план випуску.

Підприємство може випускати вироби двох типів. Норма прибутку для кожного виробу – 8 і 12 умовних одиниць відповідно. Під це замовлення виділено матеріальні й людські ресурси. Відомо, скільки ресурсів йде на виготовлення кожного виробу.

Вироби	Ресурс 1	Ресурс 2	Ресурс 3
1	2	0.5	2
2	4	0.25	2.5
Наявність ресурсів на складі	490	65	320

Питається, як потрібно спланувати виробництво виробів, щоб а) випустити їх максимальну кількість, або б) максимізувати одержуваний прибуток.

Вказівка. Спочатку розв’язати задачу для цільової функції Кількість, а потім – ту ж задачу для цільової функції Прибуток. Не забудьте обмеження!

Зверніть увагу, що в першому випадку виходить цілочисловий розв’язок (випадково!), а в другому – ні. Розв’язати цю ж задачу 2б) (цілочислово!) в Excel. Уставте діапазон розв’язку з Excel у документ MathCAD. Порівняєте цілочисловий розв’язок Excel із розв’язком MathCAD. Зверніть увагу, що розв’язок цілочислової задачі не є округленням нецілочислового розв’язку.




Задача 3. Транспортна задача.

У транспортній задачі нерівності в обмеженнях замінено на рівності. Утворюється система лінійних алгебраїчних рівнянь, але не з одним, а з множиною розв’язань, одне з яких оптимізує цільову функцію.


Задача 3А.

Необхідно щодня з першого складу перевозити в два магазини 50 товарів, а з другого складу – 70. При цьому перший магазин продає за день 40 товарів, а другий – 80 (=50+70–40).

Відомі витрати на перевезення однієї одиниці товару зі складів до магазинів (чотири константи: 1200 у. о. під час перевезення одного товару з першого складу до першого магазину, 1600 – з першого складу до другого магазину, 800 – з другого складу до першого магазину і 1000 – з другого складу до другого магазину).

Питається, як потрібно організувати перевезення (знайти значення змінних с1м1, с1м2, с2м1 і с2м2), щоб витрати були мінімальними?

Примітка. Зверніть увагу, що за найдешевшим маршрутом нічого не перевозиться. Тобто інтуїтивне розв’язання задачі: завантажити спочатку найдешевший маршрут, а вантаж, що залишився, привезти маршрутами, що залишилися, – неправильне, бо призведе до максимізації витрат.


Задача 3Б.

Розв’язати задачу про перевезення однорідних вантажів (запчастин, матеріалів, комплектуючих тощо) зі складів у Донецьку, Києві та Львові на заводи в Харкові, Полтаві, Кіровограді, Рівному й Запоріжжі, мінімізувавши витрати на перевезення. Вартість витрат пропорційна відстаням. За одну поїздку перевозиться 5 тонн вантажу.

Таблиця відстаней:

	Харків	Полтава	Вінниця	Рівне	Запоріжжя
Донецьк	283	391	812	1064	243
Київ	487	343	266	324	568
Львів	1042	898	369	215	1014

Наявність вантажу на складах:

Донецьк	310
Київ	260
Львів	280

Потреба у вантажі на заводах:

Харків	Полтава	Вінниця	Рівне	Запоріжжя
180	80	200	160	220

Розв’язання.

Вихідні дані:

			Донецьк
			Київ
			Львів

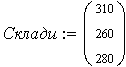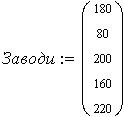i := 0..2 j := 0..4 Кількість_i,j


Цільова функція:



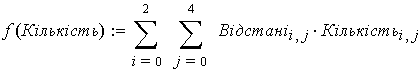
Пошук розв’язку:


Given

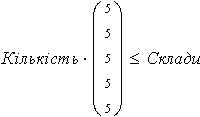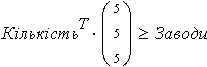	Кількість  0

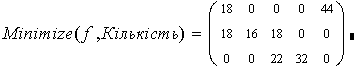
Задача 4. Задача про розміщення


Задача 4А. Є 11 будинків, в одному з яких потрібно розмістити вбудований магазин так, щоб мінімізувати суму відстаней до нього від усіх інших будинків. Координати будинків наведені в таблиці. Визначити, до якого з них треба прибудовувати магазин.

	41. 733	21. 836
	25. 851	34.81
	21. 311	21. 834
	47. 467	28. 893
	27. 477	31. 433
	23. 586	25. 207
	42. 348	34. 788
	22. 805	9. 498
	49. 147	8. 919
	36. 959	22. 873
	9.8	4. 876

Побудуйте графік, на якому відзначте всі будинки й окремим маркером – той із них, до якого буде прибудовуватися магазин.

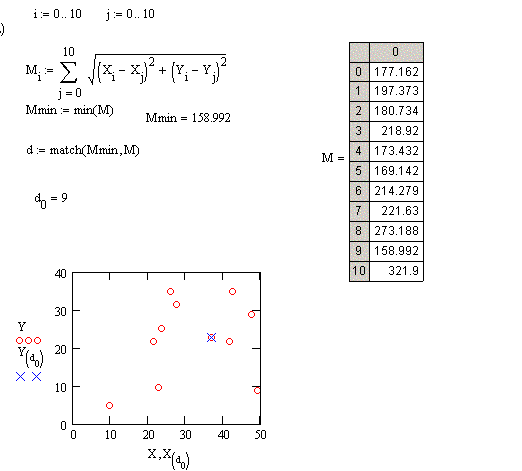
Вказівка. Сформуйте вектор із 11 елементів, заповнивши його сумами відстаней від даного будинку до всіх інших. Знайдіть його мінімальний елемент (функція min). Порядковий номер цього елемента вектора допоможе знайти функція match (z, A):

match (z, A) – шукає значення z у масиві або векторі А і знаходить його координати. При цьому результат роботи цієї функції – також вектор, тому що дане значення може міститися в масиві неодноразово. У цьому випадку координати елементів А будуть названі в порядку появи за рядками.


Розв’язання.





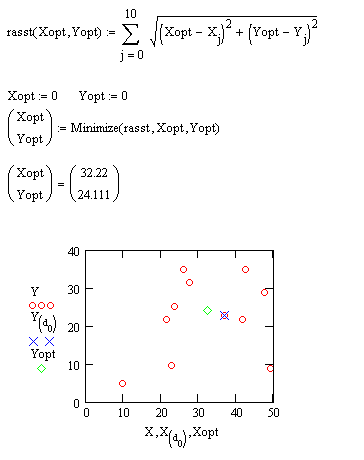
Задача 4Б. Розв’язати ту ж задачу, але тепер магазин повинен бути окремою будівлею (як і раніше треба мінімізувати відстані до всіх 11 будинків). Перемістіть попередній графік униз і доповніть його маркером із координатами нового магазину.


Розв’язання.




Задача 5. Задача про завантаження устаткування.

Побудувати модель оптимального розміщення працівників на ділянці за умови, що кожний із трьох працівників може виконувати будь-яку з трьох операцій і їх виробіток за операціями характеризується таким чином:

	Працівник 1	Працівник 2	Працівник 3
Операція 1	5	4	6
Операція 2	7	8	5
Операція 3	3	6	5

Позначимо x_ij зайнятість j-го працівника на i-й операції. Модель, за якою можна знайти таке розміщення працівників, щоб загальна продуктивність праці була найбільшою, має вигляд:

5x₁₁+4x₁₂+6x₁₃+7x₂₁+8x₂₂+5x₂₃+3x₃₁+6x₃₂+5x₃₃max

x
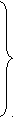
ці обмеження говорять про те, що кожний працівник виконує тільки одну операцію, і що кожну операцію буде здійснювати тільки один працівник.
₁₁+x₁₂+x₁₃=1

x₂₁+x₂₂+x₂₃=1

x₃₁+x₃₂+x₃₃=1

x₁₁+x₂₁+x₃₁=1

x₁₂+x₂₂+x₃₂=1

x₁₃+x₂₃+x₃₃=1


це обмеження говорить про те, що x_ij може набувати значень тільки 0 або 1.



x_ij(x_ij–1)=0


Розв’яжемо цю задачу в Excel і MathCAD. В Excel, щоб зазначити, що тільки x_ij = 0 або x_ij = 1, можна додати обмеження: x_ij цілочислові і ≥ 0 і ≤ 1.

У MathCAD доведеться сформувати матрицю значень x_ij(x_{ij –} 1) і вимагати у блоці given, щоб ця матриця = 0.

Розв’язання.

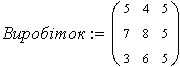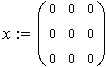		i := 0..2, j := 0..2.

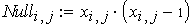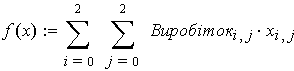
Given







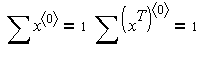
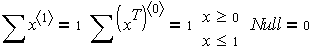
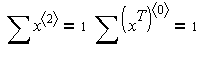
x:=Maximize(f,x)

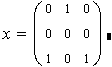	операція 1	(№ стовпця матриці відповідає порядковому номеру працівника).
	операція 2
	операція 3