Geum.ru

О. О. Метешкін, д-р техн наук, проф. Харківського військового університету; > Н. А. Кизим, д-р екон. наук, проф. Харківського

Вид материалаДокументы

Содержание


ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ ДО рОзДІЛУ 3
Подобный материал:
1   ...   18   19   20   21   22   23   24   25   26

ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

ДО рОзДІЛУ 3



Завдання 1. Розв’язати систему лінійних рівнянь: а) матричним способом; б) за допомогою функції lsolve; в) за допомогою матричних функцій в Excel (уставити фрагмент аркуша Excel у документ MathCAD).

Завдання 2. Розв’язати задачу в MathCAD і Excel (уставити фрагмент аркуша Excel у документ MathCAD). Увести змістові позначення (у тому числі в Excel – імена діапазонів).

Завдання 3. Перевірити, чи задана матриця може бути структурною матрицею торгівлі декількох країн. У випадку позитивної відповіді – знайти співвідношення національних доходів цих країн для збалансованої торгівлі.

Завдання 4. Перевірити, чи є задана матриця витрат продуктивною, застосувавши такий критерій продуктивності: матриця є продуктивною тоді і тільки тоді, коли всі властиві значення матриці А за модулем менші за одиницю.


Варіанти вихідних даних


Варіант 1.

1.

.

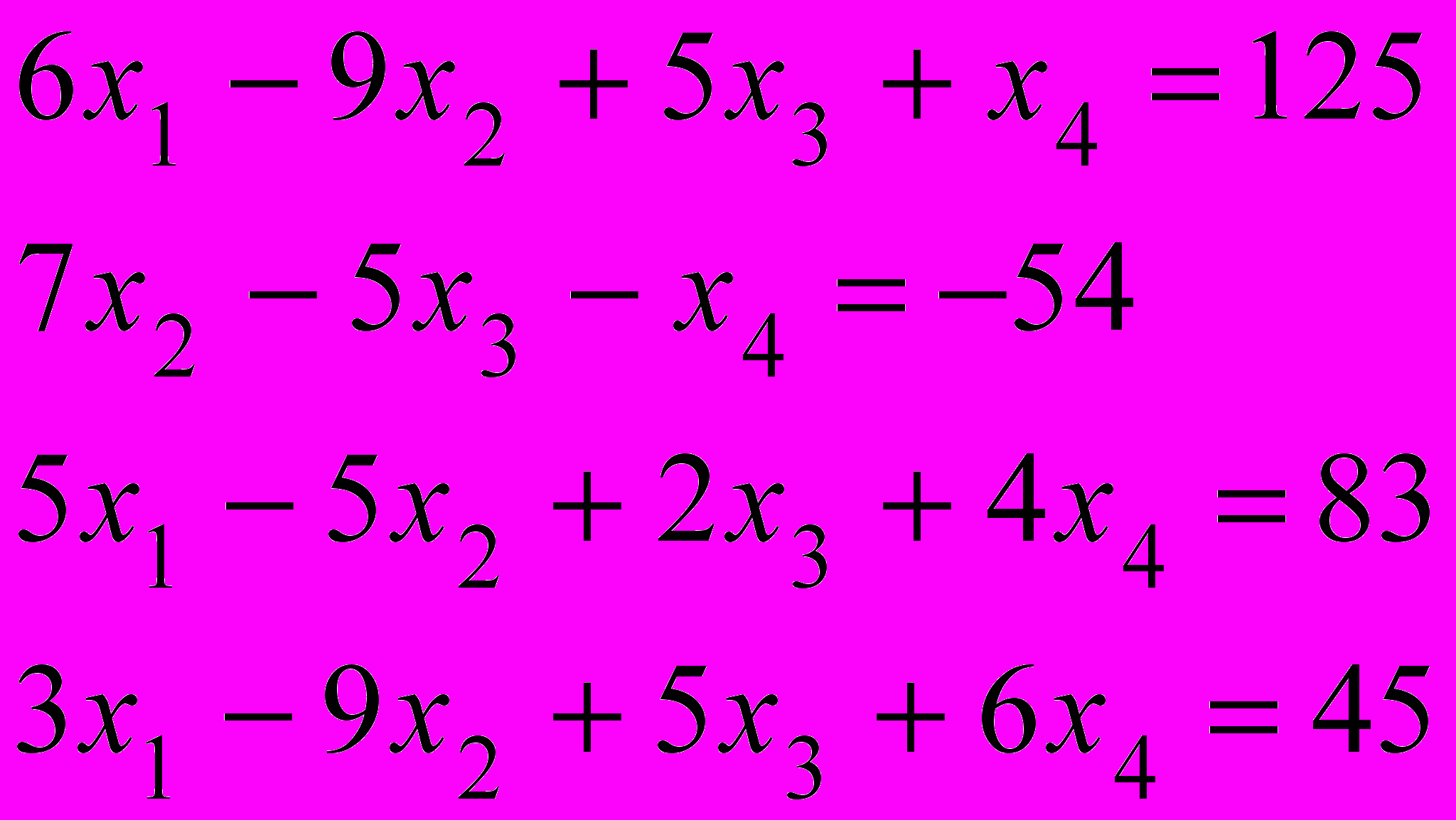
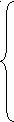2. Із пункту А в пункт В необхідно перевезти устаткування трьох типів: I типу – 2096 од., II – 2336 од., III – 2426 од. Для перевезення завод може замовити три види транспорту. Кількість устаткування кожного типу, що вміщується на певний вид транспорту, наведено в таблиці:


Тип

устаткування
Вид транспорту

Т1
Т2
Т3

I
82
72
62

II
92
62
72

III
82
102
92


Установити, скільки одиниць транспорту кожного виду необхідно для перевезення устаткування з пункту А в пункт В.


3. Матриця має вигляд:


0,319
0,303
0,641
0

0,313
0
0,176
0

0,03
0,143
0,029
0,122

0,338
0,554
0,154
0,878


4. Матриця витрат має вигляд:


0,087209
0,33853
0
0,082411

0,129845
0,494432
0,255339
0,105781

0,170543
0,321826
0,513463
0,114391

0,062016
0,231626
0,465181
0,04059



  1. Матриця міжгалузевих зв'язків, вектор цін та обсяг кінцевої продукції:

X
p
Y

37
42
289
111
3,12
47

453
288
546
388
2,4
0

76
0
281
145
1,2
39

48
541
345
249
35,7
222


Варіант 2.

1.

.

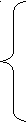
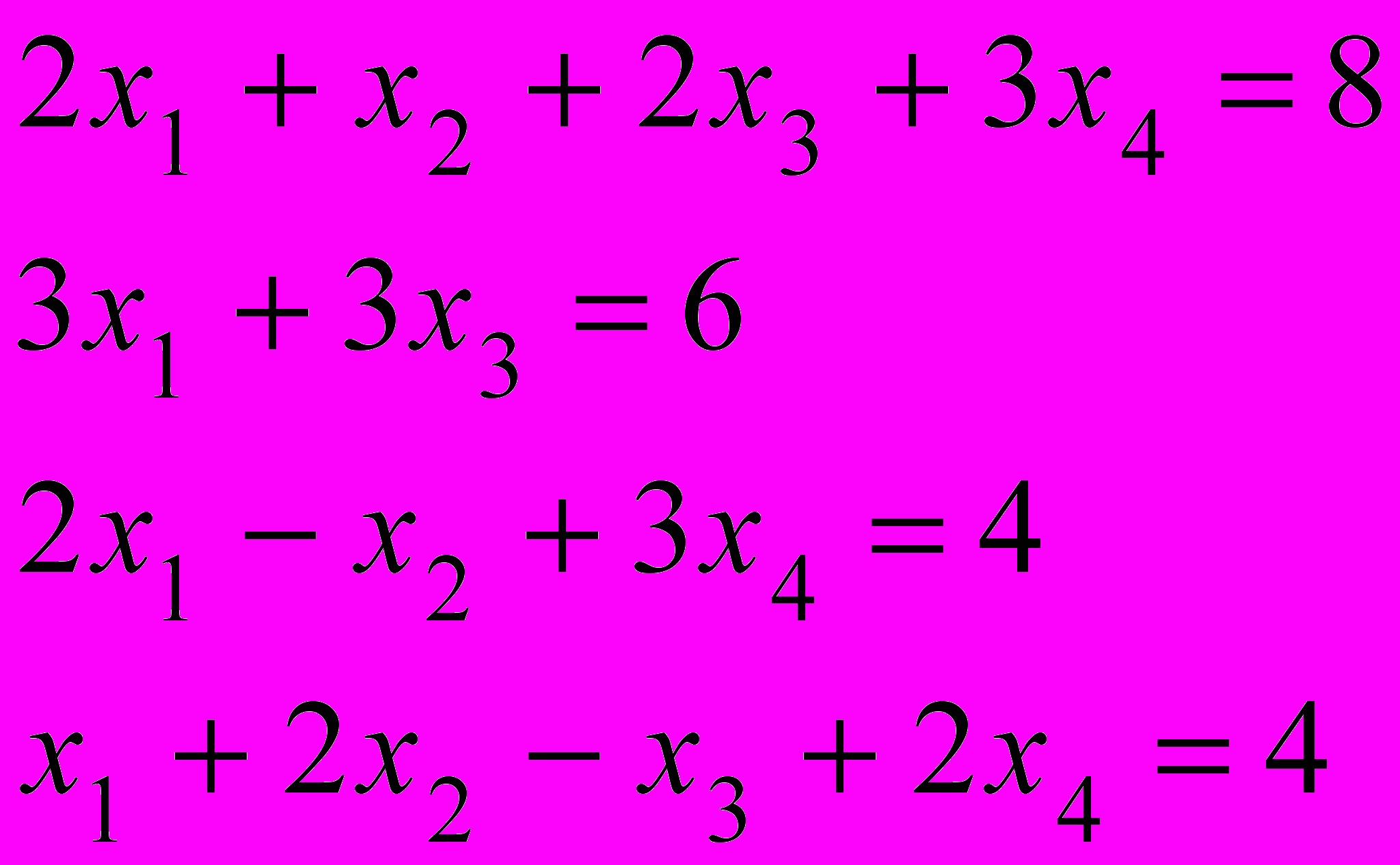2. Підприємство випускає вироби трьох видів: I, II, III. При цьому використовується сировина трьох типів: S1, S2, S3. Норми витрат кожного з типів сировини на один виріб і обсяг витрат сировини на один день задані таблицею:


Вид сиро-вини
Норми витрат на один виріб, у. о.
Витрати сировини за один день, у. о.

I
II
III

S1
1
2
5
1100

S2
3
4
3
1800

S3
5
6
2
2600


Знайти щоденний обсяг випуску кожного виду виробу.


3. Матриця має вигляд:


0,52351
0,1
0,4485
0

0,02156
0
0,1229
0,155

0,2187
0,212
0,321154
0,2354

0,236144
0,688
0,1075
0,6096


4. Матриця витрат має вигляд:


0,087209
0,2059839
0
0,01204735

0,213397
0,4944321
0,13530576
0,02541435

0,528929
0,6073265
0,51346332
0,05186378

0,424222
0,9640864
1,02600682
0,04059041


5. Матриця міжгалузевих зв’язків, вектор цін і обсяг кінцевої продукції:

x
p
Y

108
122
89
43
45,3
202

235
234
90
108
28,9
90

200
359
36
122
17,1
186

216
163
25
76
32,0
36


Варіант 3.

1.

.


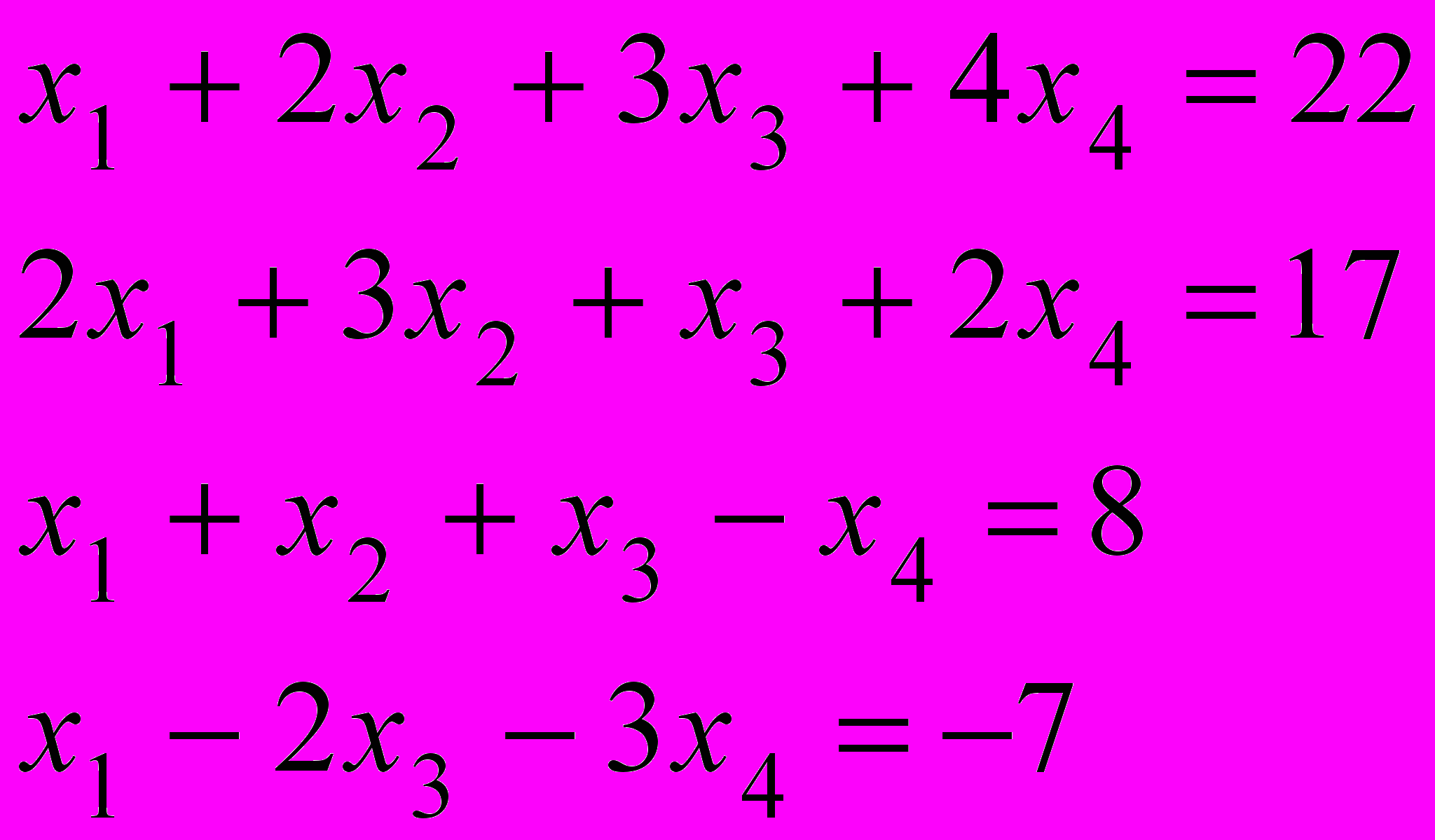
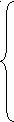2. Є три банки, кожний із яких нараховує вкладнику деякий річний відсоток (свій для кожного банку). На початку року внесок розміром 6000 грош. од. вклали в банки: 1/3 внеску – у банк 1, 1/2 внеску – у банк 2 і частину, що залишилася, – у банк 3, під кінець року сума цих внесків зросла до 7250 грош. од. Якби спочатку 1/6 внеску вклали в банк 1, 2/3 – у банк 2 і частину, що залишилася, – у банк 3, то під кінець року сума внеску склала б 7200 грош. од.; якби 1/2 внеску поклали в банк 1, 1/6 – у банк 2 і 1/3 – у банк 3, то сума внесків наприкінці року склала б 7250 грош. од. Визначити, який відсоток виплачує кожний банк?

3. Матриця має вигляд:


0,641
0,428
0,303
0,319

0,176
0,221
0,554
0,313

0,154
0,229
0
0,03

0,029
0,122
0,143
0,338

4. Матриця витрат має вигляд:


0,070342
0,032597
1,014035
0,006905

0,662474
0,17194
1,473684
0,018565

0,201813
0
0,379217
0,003469

1,044165
4,804403
13,85121
0,177224


5. Матриця міжгалузевих зв’язків, вектор цін і обсяг кінцевої продукції:

x
p
Y

59
45
56
36
4,74
73

76
121
94
43
1,66
144

69
201
34
55
2,07
62

82
69
22
77
6,8
72


Варіант 4.

1.

.

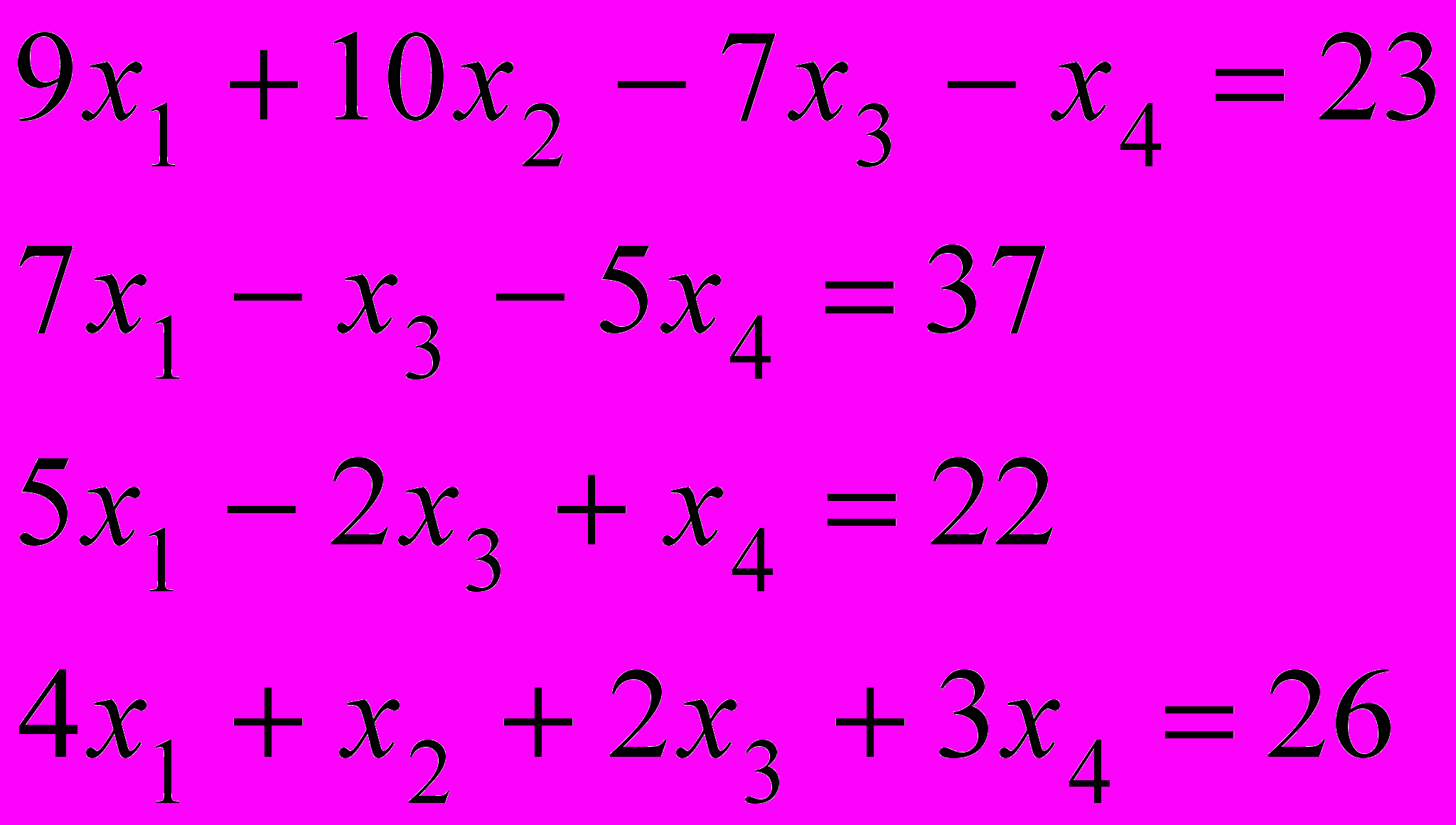
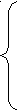2. Підприємство випускає вироби трьох видів: I, II, III. При цьому використовується сировина трьох типів: S1, S2, S3. Норми витрат кожного з типів сировини на один виріб і обсяг витрат сировини на один день задані таблицею:


Вид сировини
Норми витрат на один виріб, у. о.
Витрати сировини на один день, у. о.

I
II
III

S1
2
7
1
390

S2
4
5
2
420

S3
6
3
1
350


Знайти щоденний обсяг випуску кожного виду виробів.


3. Матриця має вигляд:


0,21173
0,6096
0,236188
0,107506

0,688270
0,155
0,218742
0,4485

0,1
0,2354
0,52351
0,321154

0
0
0,02156
0,12284

4. Матриця затрат має вигляд:


0,070342
0,025075
0,390013
0,079004

0,861217
0,17194
0,736842
0,276157

0,524715
0
0,379217
0,103203

0,091255
0,322985
0,465587
0,177224


5. Матриця міжгалузевих зв’язків, вектор цін і обсяг кінцевої продукції:


x
p
Y

101
89
98
45
45,7
45

19
90
54
121
37,8
28

25
36
72
201
39,4
17

87
25
43
69
33
32


Варіант 5.

1.

.

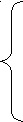2. Із двох заводів поставляються автомобілі для двох автогосподарств, потреби яких відповідно 200 й 300 автомобілів. Перший завод випустив 350 автомобілів, а другий – 150 автомобілів. Витрати на перевезення автомобілів із заводів у кожне автогосподарство задані таблицею:


Завод
Витрати на перевезення в автогосподарство,

грош. од.




Автогосподар-ство 1
Автогосподар-ство 2

Завод 1
15
20

Завод 2
8
25


Мінімальні витрати на перевезення дорівнюють 7950 грош. од. Знайдити оптимальний план перевезення автомобілів.

3. Матриця має вигляд:


0,122
0,176
0,303
0,03

0,229
0,641
0,554
0,313

0,221
0,154
0
0,319

0,428
0,029
0,143
0,338

4. Матриця витрат має вигляд:


0,242105263
0,022508
0,021799
0,0043859

2,39196836
0,169149
0,334082
0

5,466334043
0,070209
0,032239
0,034611

19,83751141
2,377795
0,825706
0,0422535


5. Матриця міжгалузевих зв’язків, вектор цін і обсяг кінцевої продукції:


x
p
Y

34
555
52
84
5,6
29

77
251
81
0
9,8
10

235
234
90
108
41,3
15

37
44
55
95
33,3
66