О. О. Метешкін, д-р техн наук, проф. Харківського військового університету; > Н. А. Кизим, д-р екон. наук, проф. Харківського

Вид материала

Документы

Подобный материал:

• А. В. Ковалевська Рецензенти: доцент, канд екон наук, доцент Харківського національного, 739.76kb.
• А. А. Гвоздев руководительтемы; доктора техн наук, 3579.39kb.
• Інформаційні технології в журналістиці: вітчизняний І світовий досвід Київ 2002, 8272.38kb.
• Дипломных проектов по специальностям, 283.96kb.
• Конкурс-захист проходив на базі Харківського національного університету ім. В. Н. Каразіна,, 342.15kb.
• «Сторінки історії Харківського університету за архівними документами», 72.28kb.
• Міжнародна журналістика – 2002 київ 2002, 2743.9kb.
• Приглашение и программа разнообразие почв и биоты северной и центральной азии, 521.14kb.
• Строительные нормы и правила бетонные и железобетонные конструкции, 3448.03kb.
• Надійності та безпеки в будівництві, 692.13kb.

Варіант 6.

1.

.

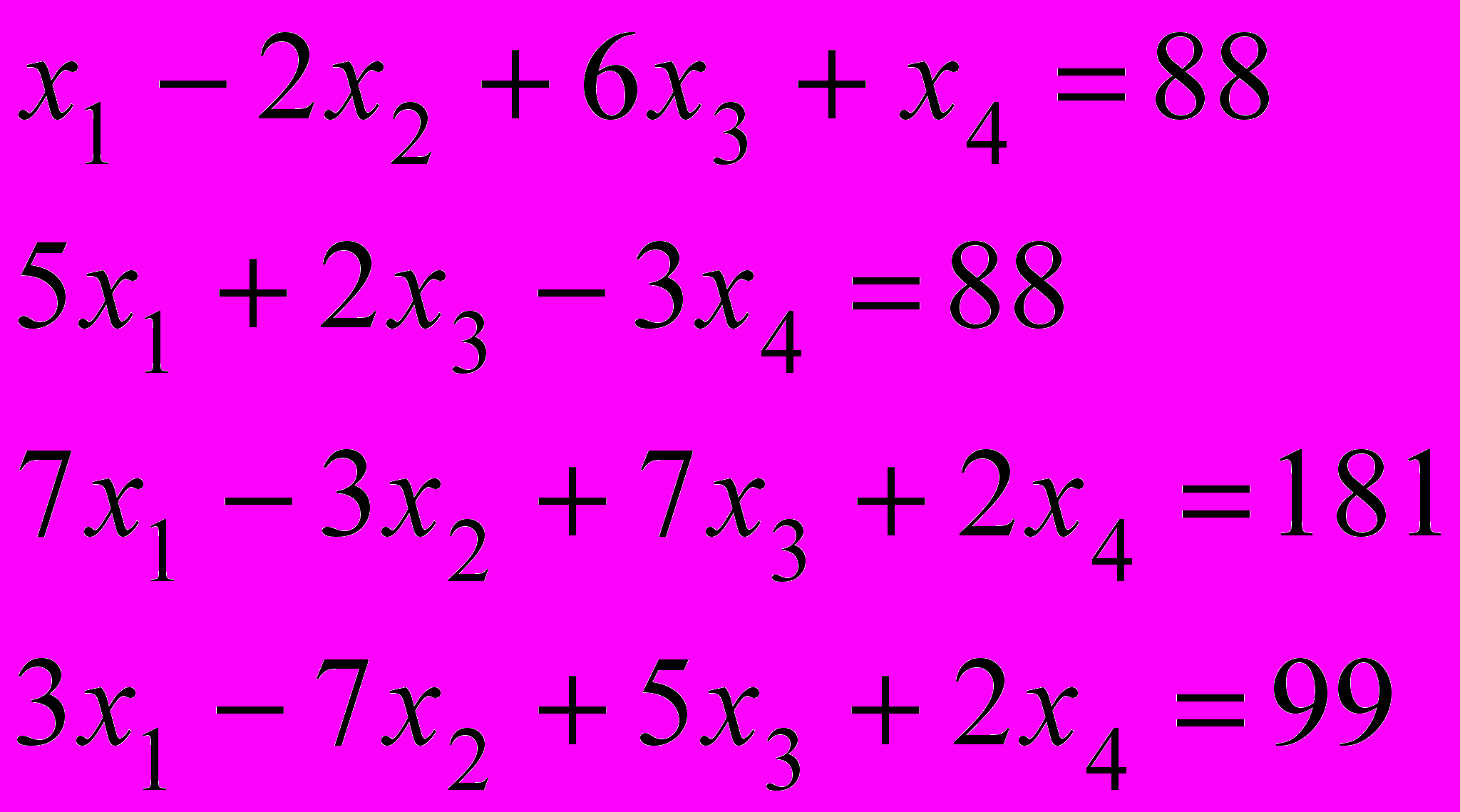
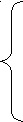2. Підприємство випускає продукцію трьох видів А, В, С. Рівень випуску лімітується обмеженістю ресурсів. Усі числові дані наведені в таблиці:

Ресурси	Запас ресурсу	Норма затрат на одиницю продукції
		А	В	С
Сировина, кг	24	5	7	4
Матеріали, кг	75	10	5	20
Устаткування, од.	10	5	2	1

Знайти план випуску продукції.

3. Матриця має вигляд:

0.155	0.236188	0.1	0.107506
0.6096	0.52351	0	0.4485
0.2354	0.218742	0.21173	0.321154
0	0.02156	0.68827	0.12284

4. Матриця затрат має вигляд:

0,242105263	0,114166	0,188256	0,2599232
0,471578947	0,169149	0,568797	0
0,632982456	0,041237	0,032239	0,237516
0,334736842	0,203513	0,120322	0,0422535

5. Матриця міжгалузевих зв’язків, вектор цін і обсяг кінцевої продукції:

x				p	Y
45	304	0	67	3,45	100
67	444	275	86	5,67	26
88	289	553	93	10,7	54
32	208	501	33	23,6	39

Варіант 7.

1.

.

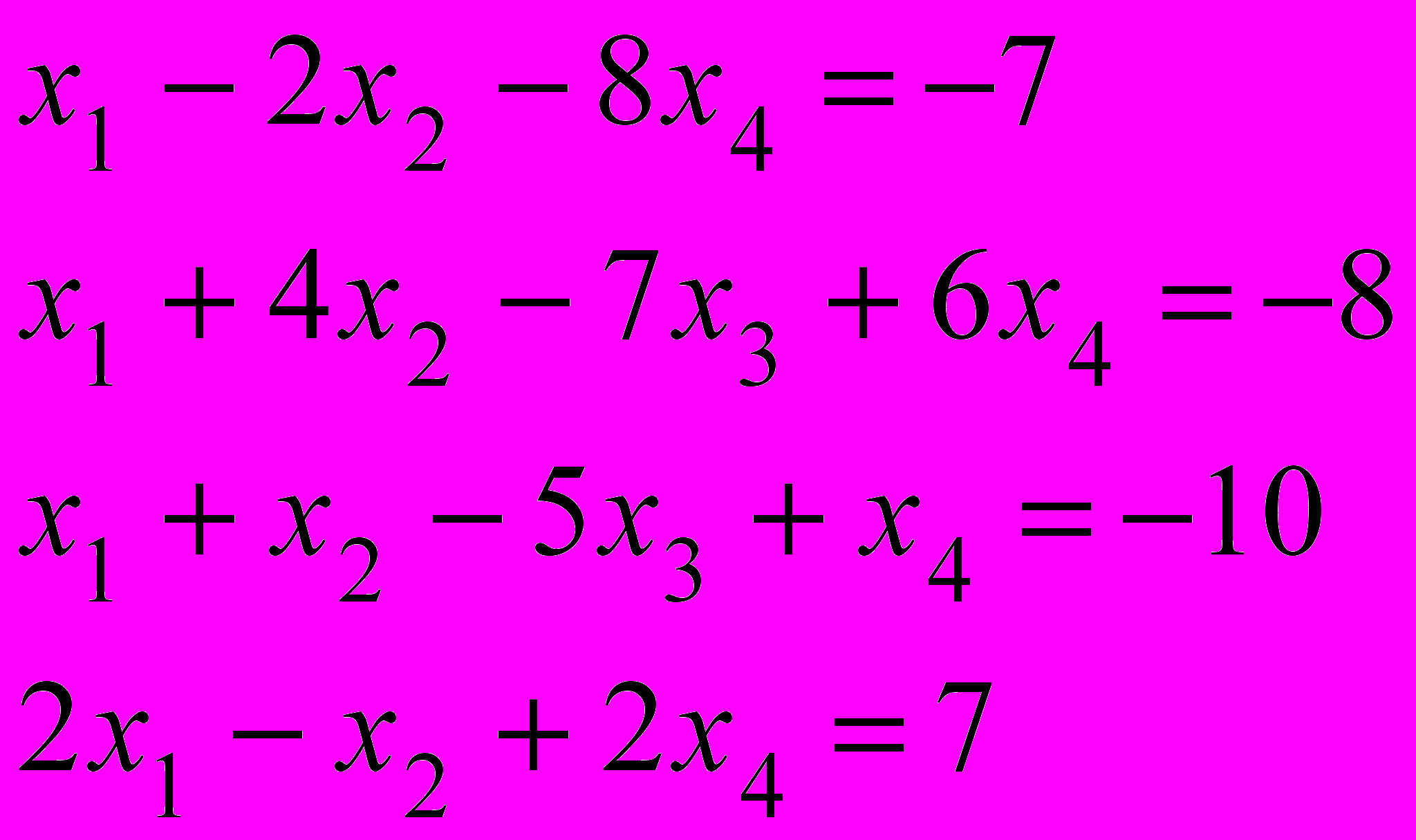
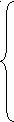2. Цех випускає 3 види виробів: I, II, III. При цьому застосовуються три виробничі процеси: штампування, складання і фарбування. Інтенсивність (у людино-годинах за період) даних процесів становить відповідно 40, 40 і 80, а трудомісткість кожного процесу при виробництві продукції задається матрицею:


,

де a_ij – кількість людино-годин, потрібна для i-го процесу обробки одиниці виробу j-го виду. Потужності кожного процесу обробки використовуються цілком. Написати в матричній формі систему рівнянь, що характеризує рівність використовуваних і наявних потужностей для кожного процесу. Визначити, який випуск кожного виду продукції.

3. Матриця має вигляд:

0,338	0,428	0,176	0,303
0,03	0,122	0,029	0,554
0,319	0,221	0,641	0,143
0,313	0,229	0,154	0

4. Матриця витрат має вигляд:





5. Матриця міжгалузевих зв’язків, вектор цін і обсяг кінцевої продукції:

x				p	Y
378	0	0	29	41,7	92
200	0	172	35	3,66	100
45	144	37	331	1,23	48
123	88	39	86	33,8	76

Варіант 8.

1.

.

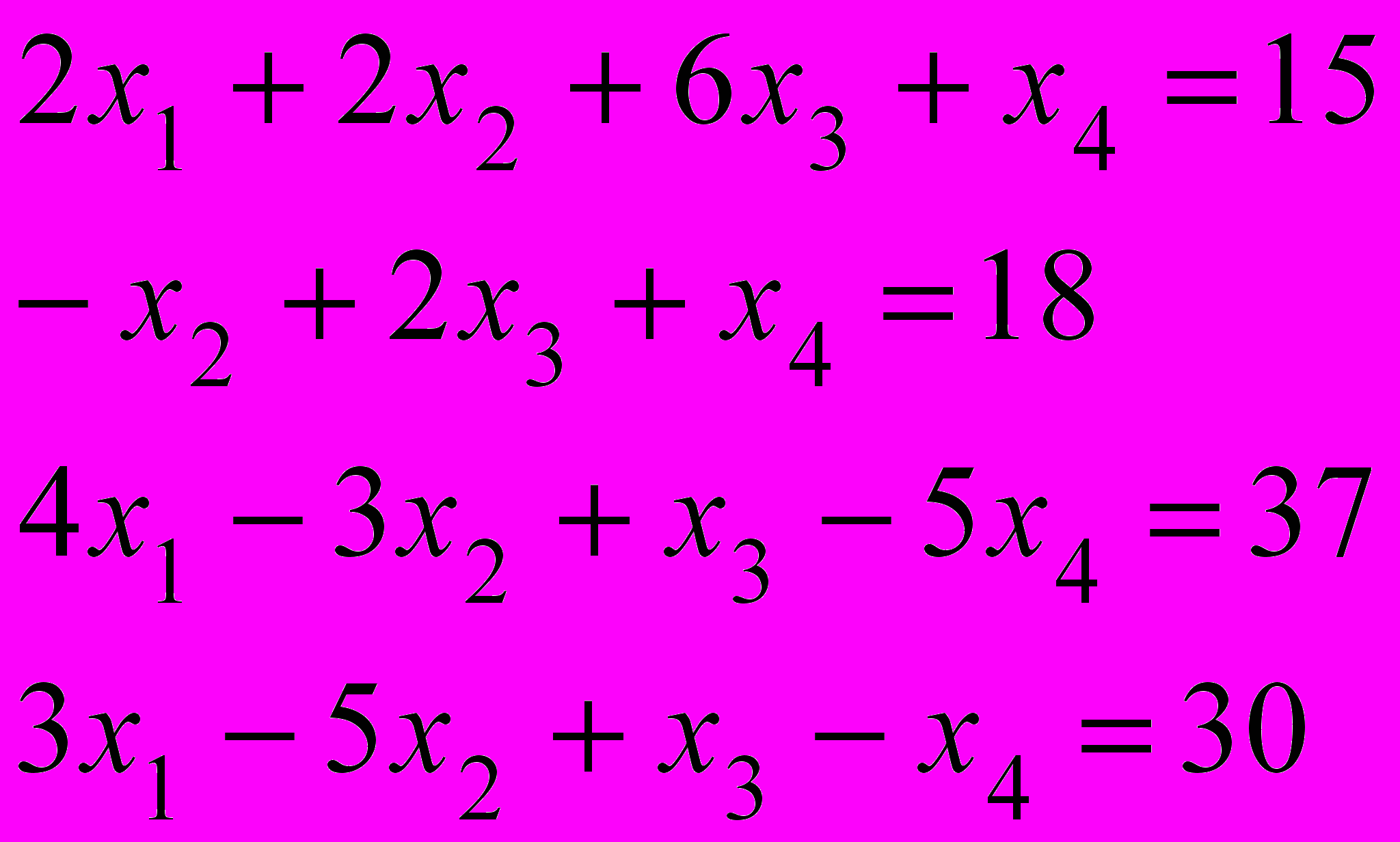
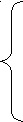2. Є три банки, кожний із яких нараховує вкладнику деякий річний відсоток (свій для кожного банку). На початку року внесок розміром 6000 грош. од. вклали в банки: 1/3 внеску – у банк 1, 1/2 внеску – у банк 2 і частину, що залишилася, – у банк 3, під кінець року сума цих внесків збільшилася до 7250 грош. од. Якби спочатку 1/6 внеску вклали в банк 1, 2/3 – у банк 2 і частину, що залишилася, – у банк 3, то під кінець року сума внесків склала б 7200 грош. од.; якби 1/2 внеску поклали в банк 1, 1/6 – у банк 2 і 1/3 – у банк 3, то сума внесків наприкінці року склала б 7250 грош. од. Визначити, який відсоток виплачує кожний банк?

3. Матриця має вигляд:

0,21173	0,107506	0,6096	0,236188
0	0,12284	0,2354	0,218742
0,1	0,321154	0,155	0,02156
0,68827	0,4485	0	0,52351

4. Матриця витрат має вигляд:





5. Матриця міжгалузевих зв’язків, вектор цін і обсяг кінцевої продукції:

x				p	Y
266	67	63	137	0,54	196
191	488	106	49	0,99	99
77	251	81	0	9	109
49	17	33	188	23,4	300

Варіант 9.

1.



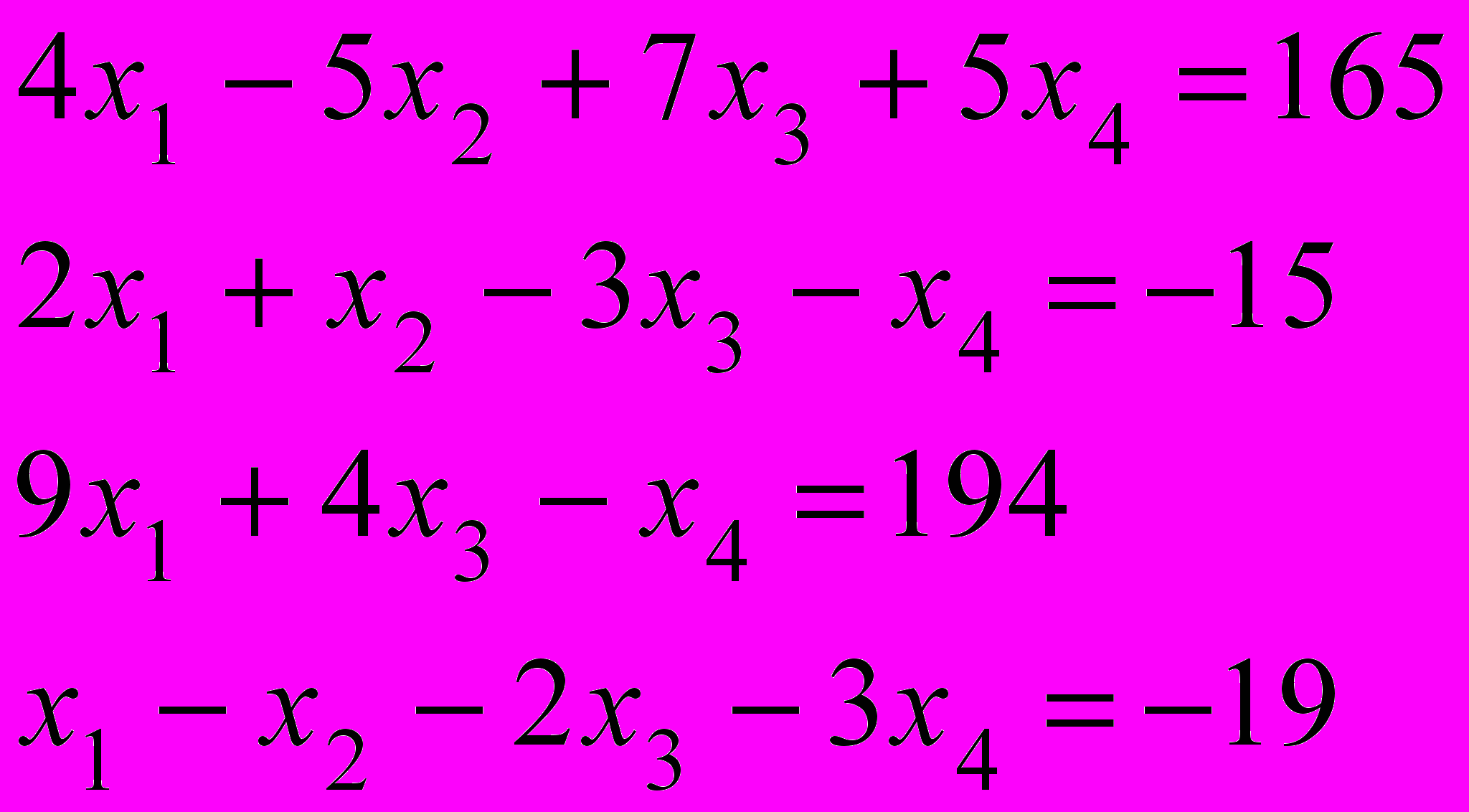
2. Із двох заводів поставляються агрегати для двох господарств, потреби яких відповідно 200 й 300 агрегатів. Перший завод випустив 350 агрегатів, а другий – 150 агрегатів. Витрати на перевезення цих агрегатів із заводів у кожне господарство задані таблицею:

Завод	Витрати на перевезення в автогосподарство, грош. од.
	Господарство 1	Господарство 2
Завод 1	15	20
Завод 2	8	25

Мінімальні витрати на перевезення дорівнюють 7950 грош. од. Знайти оптимальний план перевезення агрегатів.

3. Матриця має вигляд:

0,7	0,5	0
0,1	0,5	0,1
0,2	0	0,9

4. Матриця затрат має вигляд:

0,070342	0,025075	0,390013	0,079004
0,861217	0,17194	0,736842	0,276157
0,524715	0	0,379217	0,103203
0,091255	0,322985	0,465587	0,177224

5. Матриця міжгалузевих зв’язків, вектор цін і обсяг кінцевої продукції:

x				p	Y
0	18	36	144	3,12	47
72	17	55	58	2,40	0
37	43	43	99	1,20	039
39	43	15	0	35,7	222

Варіант 10.

1.

.

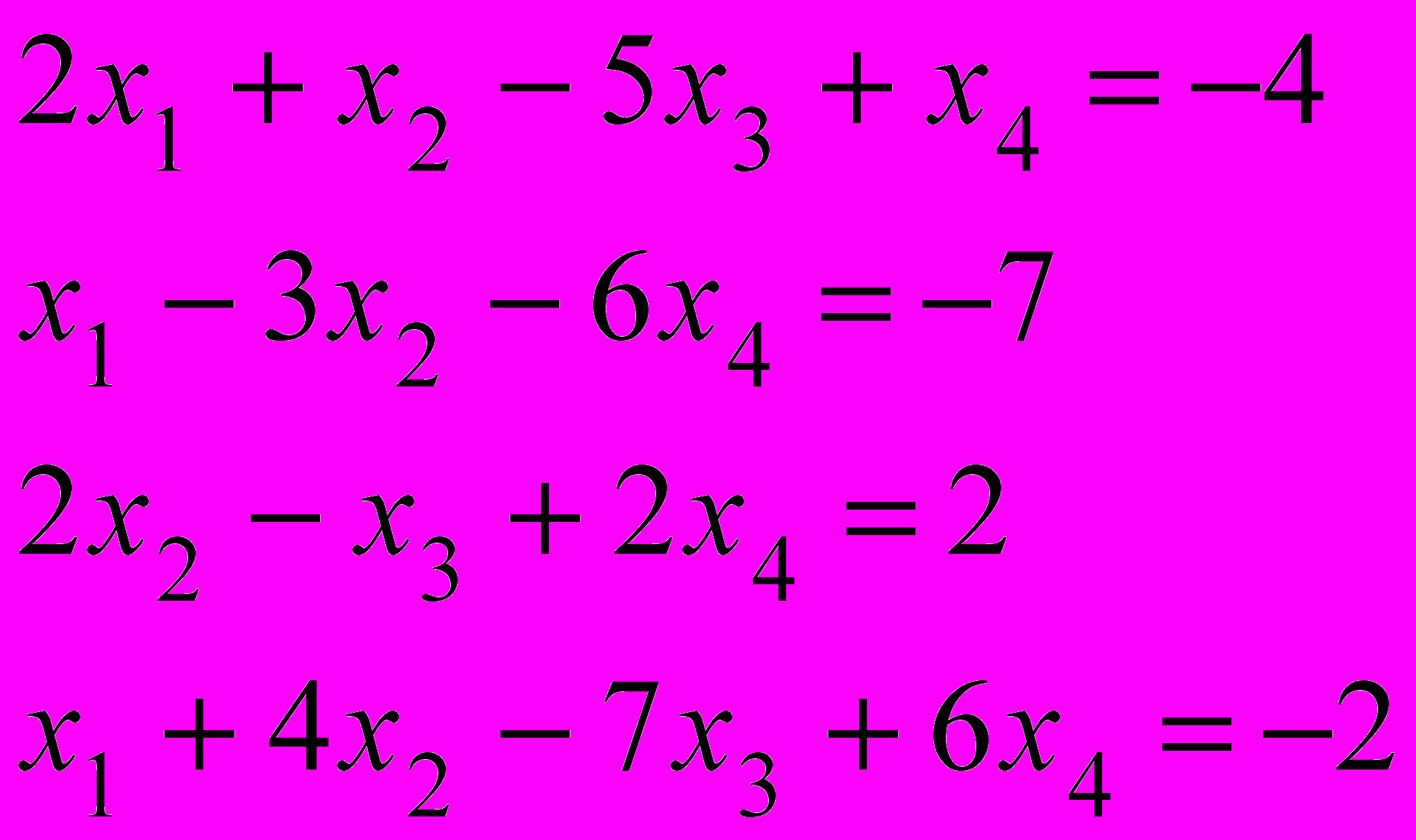
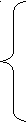2. В економіці й господарській діяльності важливу роль відіграє припущення, що механізм ринкової конкуренції зрушує ціну на продукт настільки, що попит і пропозиція стають рівними одне одному. Припустімо, що функція попиту на товари для деякого періоду часу має вигляд: x1=12000–5x2, де x1 – ціна товару, а x2 – відповідна його кількість. Нехай функція пропозиції має вигляд: x1=3000–x2. Визначити, за яких умов x1 і x2 настає рівновага? Розв’язати задачу матричним методом.

3. Матриця має вигляд:

0.338	0.176	0.428	0.554
0.319	0.641	0.221	0.303
0.03	0.029	0.122	0.143
0.313	0.154	0.229	0

4. Матриця витрат має вигляд:

0,087209	0,2059839	0	0,01204735
0,213397	0,4944321	0,13530576	0,02541435
0,528929	0,6073265	0,51346332	0,05186378
0,424222	0,9640864	1,02600682	0,04059041

5. Матриця міжгалузевих зв’язків, вектор цін і обсяг кінцевої продукції:

x				p	Y
27	0	0	98	45,7	100
39	74	0	54	37,8	324
67	88	77	72	39,4	265
55	66	23	43	33	456

Варіант 11.

1.



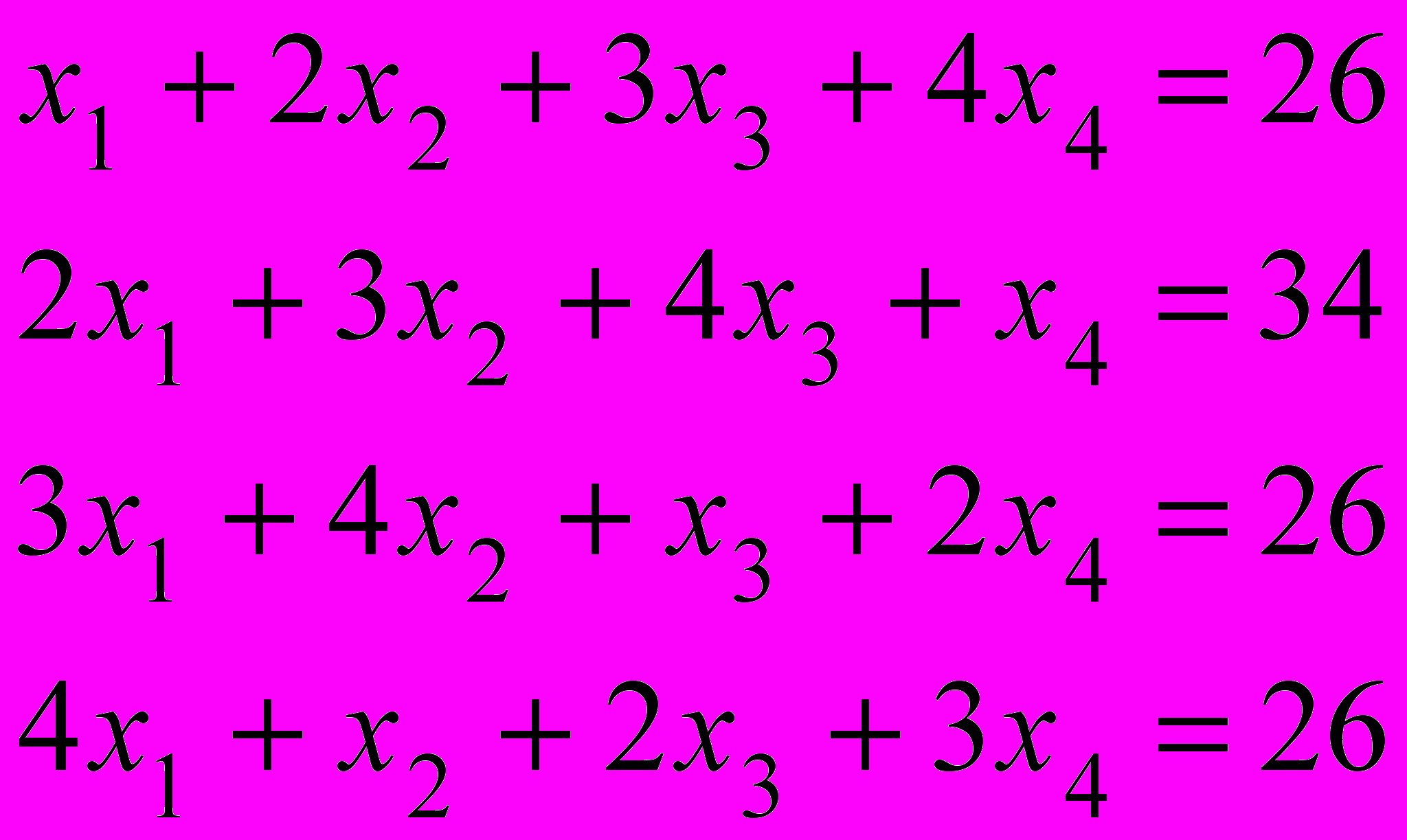
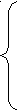
2. Підприємство випускає продукцію трьох видів А, В, С. Рівень випуску лімітується обмеженістю ресурсів. Усі числові дані наведені в таблиці:

Ресурси	Запас ресурсу	Норма затрат на одиницю продукції
		А	В	С
Сировина, кг	24	5	7	4
Матеріали, кг	75	10	5	20
Устаткування, од.	10	5	2	1

Знайти план випуску продукції.

3. Матриця має вигляд:

0,1550	0	0,4485	0,236188
0	0,211730	0,321154	0,218742
0,2354	0,68827	0,12284	0,02156
0,6096	0,1	0,107506	0,52351

4. Матриця затрат має вигляд:

0,242105263	0,022508	0,021799	0,0043859
2,39196836	0,169149	0,334082	0
5,466334043	0,070209	0,032239	0,034611
19,83751141	2,377795	0,825706	0,0422535

5. Матриця міжгалузевих зв’язків, вектор цін і обсяг кінцевої продукції:

x				p	Y
108	122	89	43	5,3	222
235	234	90	108	8,9	90
200	359	36	122	7,1	180
216	163	25	76	2,0	39

Варіант 12.

1.

.

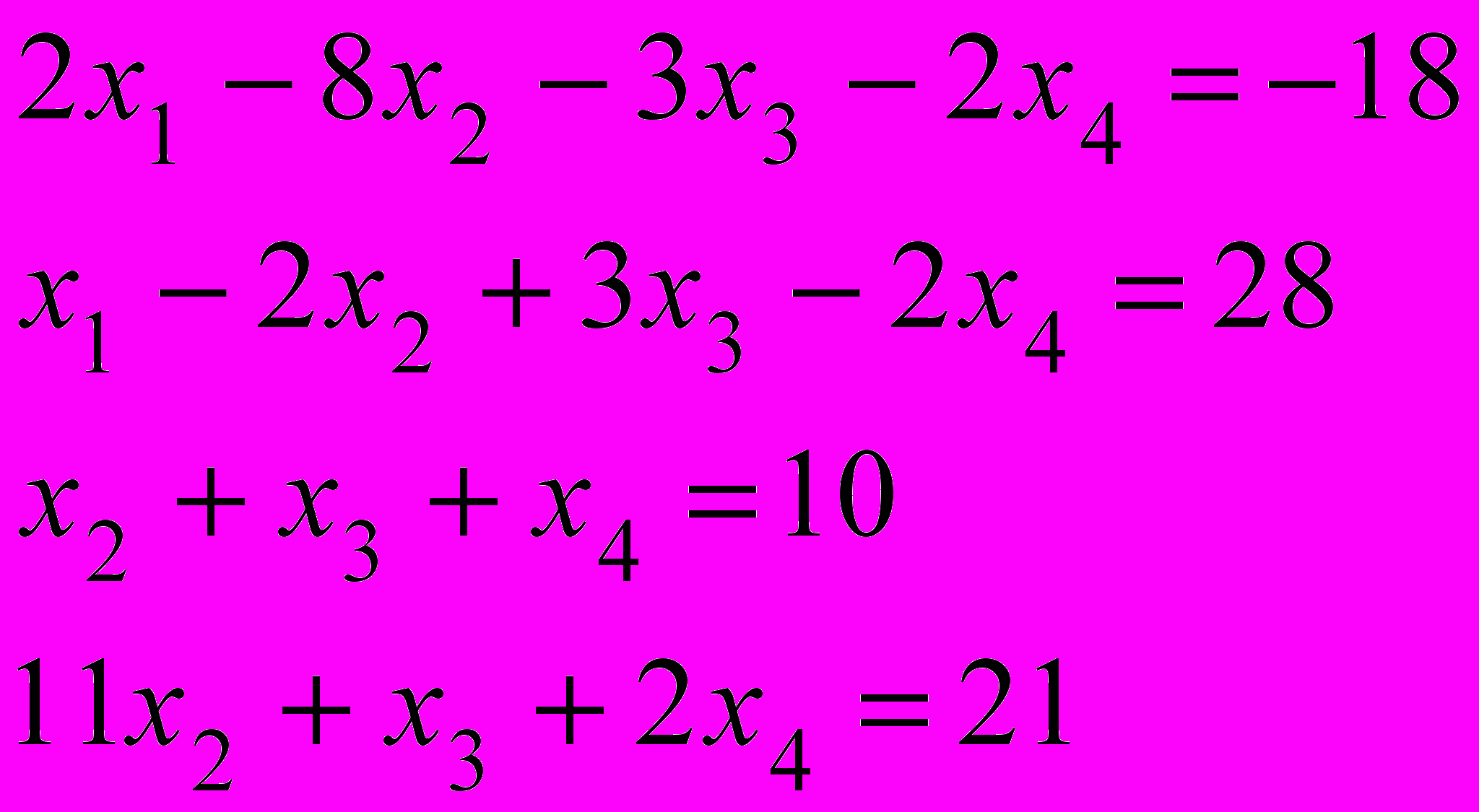
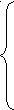2. Із пункту А в пункт В необхідно перевезти устаткування трьох типів: I – 95 од., II – 100 од., III – 185 од. Для перевезення завод може замовити три види транспорту. Кількість устаткування кожного типу, що вміщується на певний вид транспорту, наведено в таблиці:

Тип устаткування	Вид транспорту
	Т1	Т2	Т3
I	3	2	1
II	4	1	2
III	3	5	4

Установити, скільки одиниць транспорту кожного виду необхідно для перевезення устаткування з пункту А в пункт В.

3. Матриця має вигляд:

1/4	1/2	1/3
1/2	1/2	1/3
1/4	0	1/3

4. Матриця витрат має вигляд:

0,087209	0,2059839	0	0,01204735
0,213397	0,4944321	0,13530576	0,02541435
0,528929	0,6073265	0,51346332	0,05186378
0,424222	0,9640864	1,02600682	0,04059041

5. Матриця міжгалузевих зв’язків, вектор цін і обсяг кінцевої продукції:

x				p	Y
59	45	56	36	45,3	202
76	121	94	43	28,9	90
69	201	34	55	171,1	186
82	69	22	77	32,0	36

Варіант 13.

1.



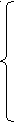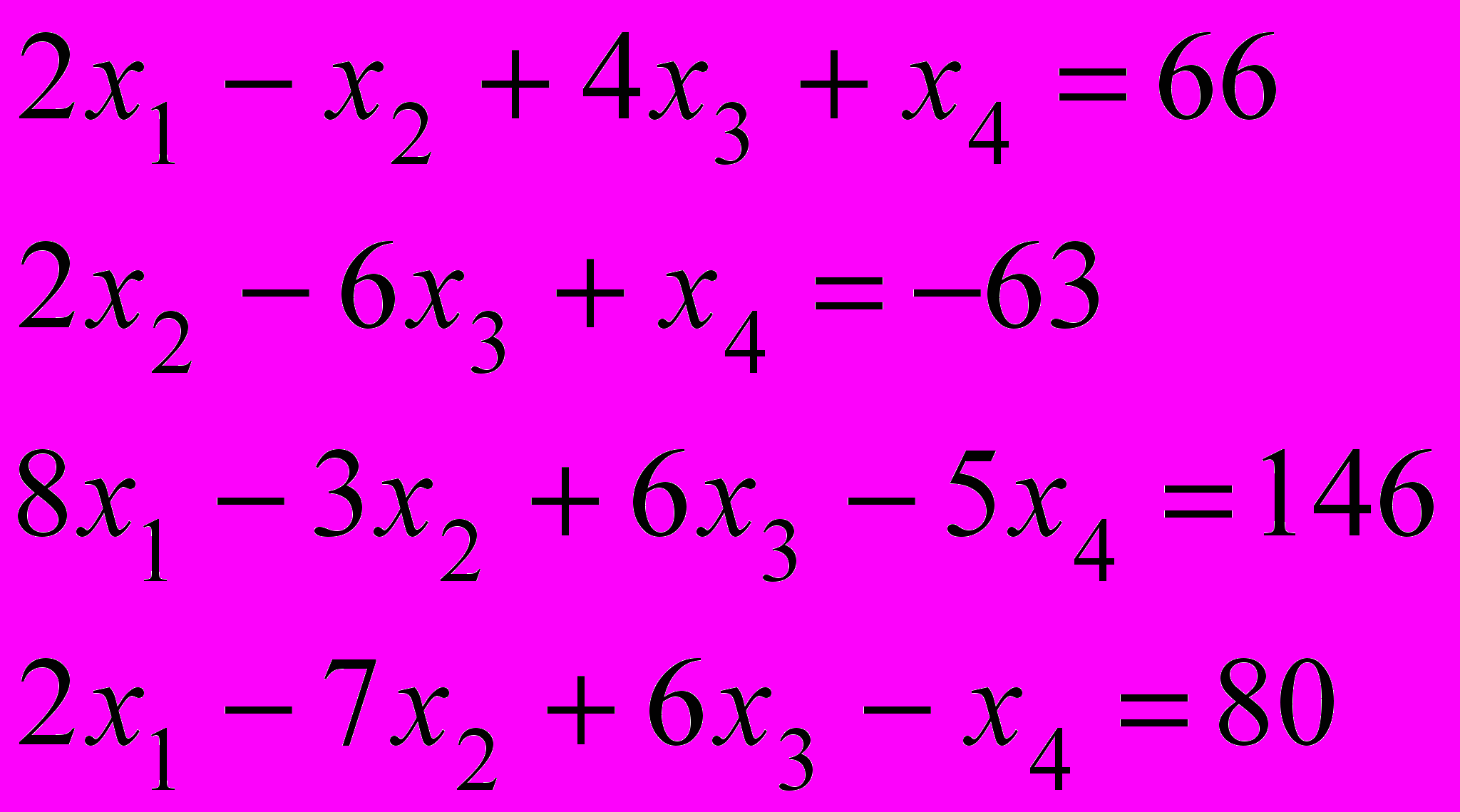
2. Підприємство випускає продукцію трьох видів А, В, С. Рівень випуску лімітується обмеженістю ресурсів. Усі числові дані наведені в таблиці:

Ресурси	Запас ресурсу	Норма затрат на одиницю продукції
		А	В	С
Сировина, кг	24	5	7	4
Матеріали, кг	75	10	5	20
Устаткування, од.	10	5	2	1

Знайти план випуску продукції.

3. Матриця має вигляд:

0,21173	0	0,321154	0,236188
0	0,155	0,4485	0,218742
0,1	0,2354	0,12284	0,02156
0,68827	0,6096	0,107506	0,52351

4. Матриця витрат має вигляд:

0,242105263	0,022508	0,021799	0,0043859
2,39196836	0,169149	0,334082	0
5,466334043	0,070209	0,032239	0,034611
19,83751141	2,377795	0,825706	0,0422535

5. Матриця міжгалузевих зв’язків, вектор цін і обсяг кінцевої продукції:

x				p	Y
34	555	52	84	15,6	39
77	251	81	0	29,8	19
235	234	90	108	1,3	19
37	44	55	95	3,3	60

Варіант 14.

1.

.

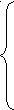2. Із пункту А в пункт В необхідно перевезти устаткування трьох типів: I – 95 од., II – 100 од., III – 185 од. Для перевезення завод може замовити три види транспорту. Кількість устаткування кожного типу, що вміщується на певний вид транспорту, наведено в таблиці:

Тип устаткуван-ня	Вид транспорту
	Т1	Т2	Т3
I	3	2	1
II	4	1	2
III	3	5	4

Установити, скільки одиниць транспорту кожного виду необхідно для перевезення устаткування з пункту А в пункт В.

3. Матриця має вигляд:

0,6	0,8	0
0,3	0,1	0,2
0,1	0,1	0,8

4. Матриця витрат має вигляд:

0,070342	0,025075	0,390013	0,079004
0,861217	0,17194	0,736842	0,276157
0,524715	0	0,379217	0,103203
0,091255	0,322985	0,465587	0,177224

5. Матриця міжгалузевих зв’язків, вектор цін і обсяг кінцевої продукції:

x				p	Y
27	0	67	98	14,2	27
39	74	0	54	22,1	39
67	88	77	72	17,8	65
55	66	23	43	9,5	18

Варіант 15.

1.

.

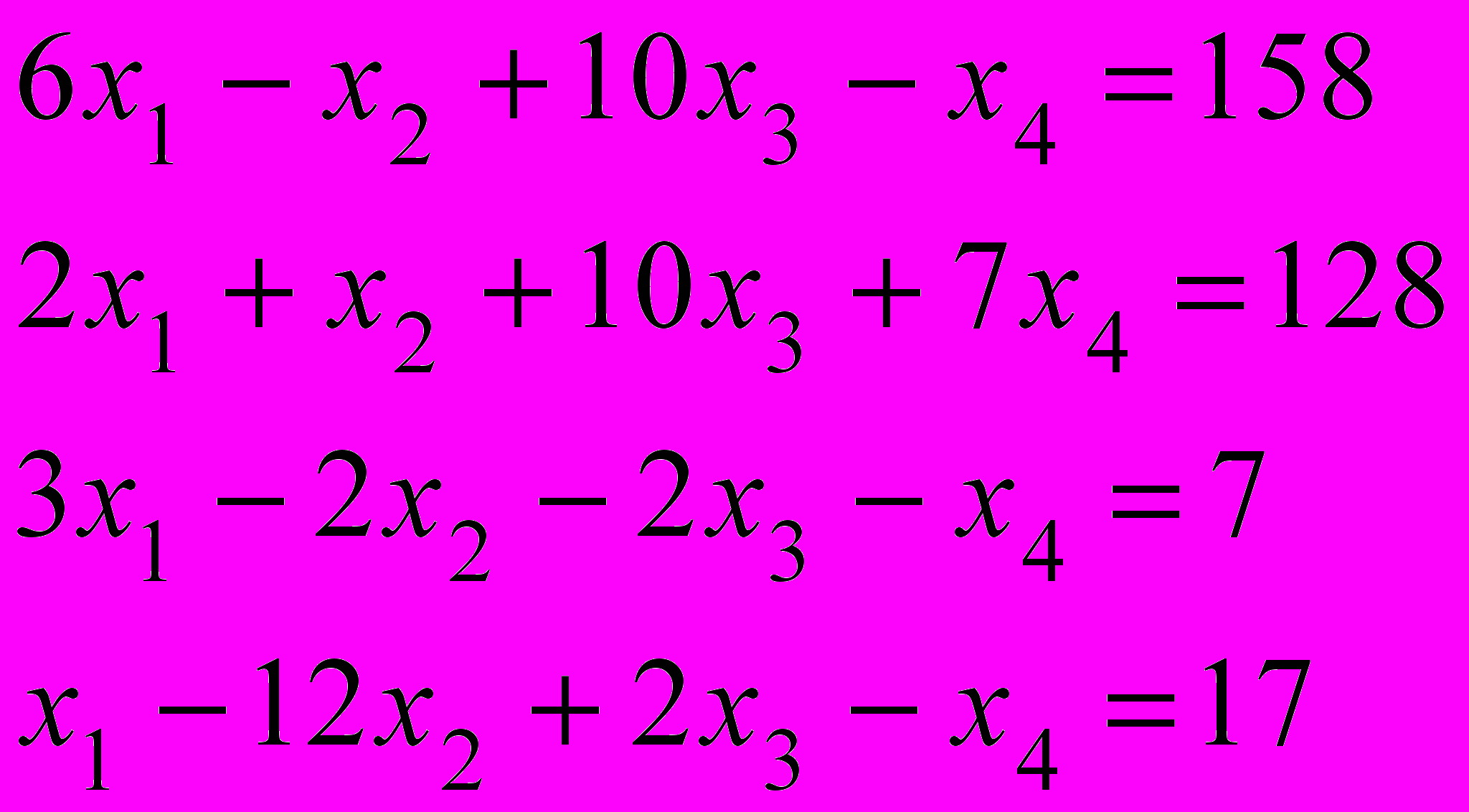
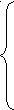2. Підприємство випускає вироби трьох видів: I, II, III. При цьому використовується сировина трьох типів: S1, S2, S3. Норми витрат кожного з типів сировини на один виріб і обсяг витрат сировини на один день задані таблицею:

Вид сировини	Норми витрат на один виріб, у. о.			Витрати сировини на один день, у. о.
	I	II	III
S1	9	3	4	820
S2	7	1	6	820
S3	5	2	2	460

Знайти щоденний обсяг випуску кожного виду виробів.

3. Матриця має вигляд:

0,338	0,176	0,8780	0,554
0,319	0,641	0	0,303
0,03	0,029	0,122	0,143
0,313	0,154	0	0

4. Матриця витрат має вигляд:

0.21173	0.107506	0.6096	0.236188
0	0.12284	0.2354	0.218742
0.1	0.321154	0.155	0.02156
0.68827	0.4485	0	0.52351

5. Матриця міжгалузевих зв’язків, вектор цін і обсяг кінцевої продукції:

x				p	Y
47	42	289	111	5,1	57
453	277	530	388	2,40	0
276	0	281	145	1,20	39
48	539	345	249	5,7	200

Варіант 16.

1.

.

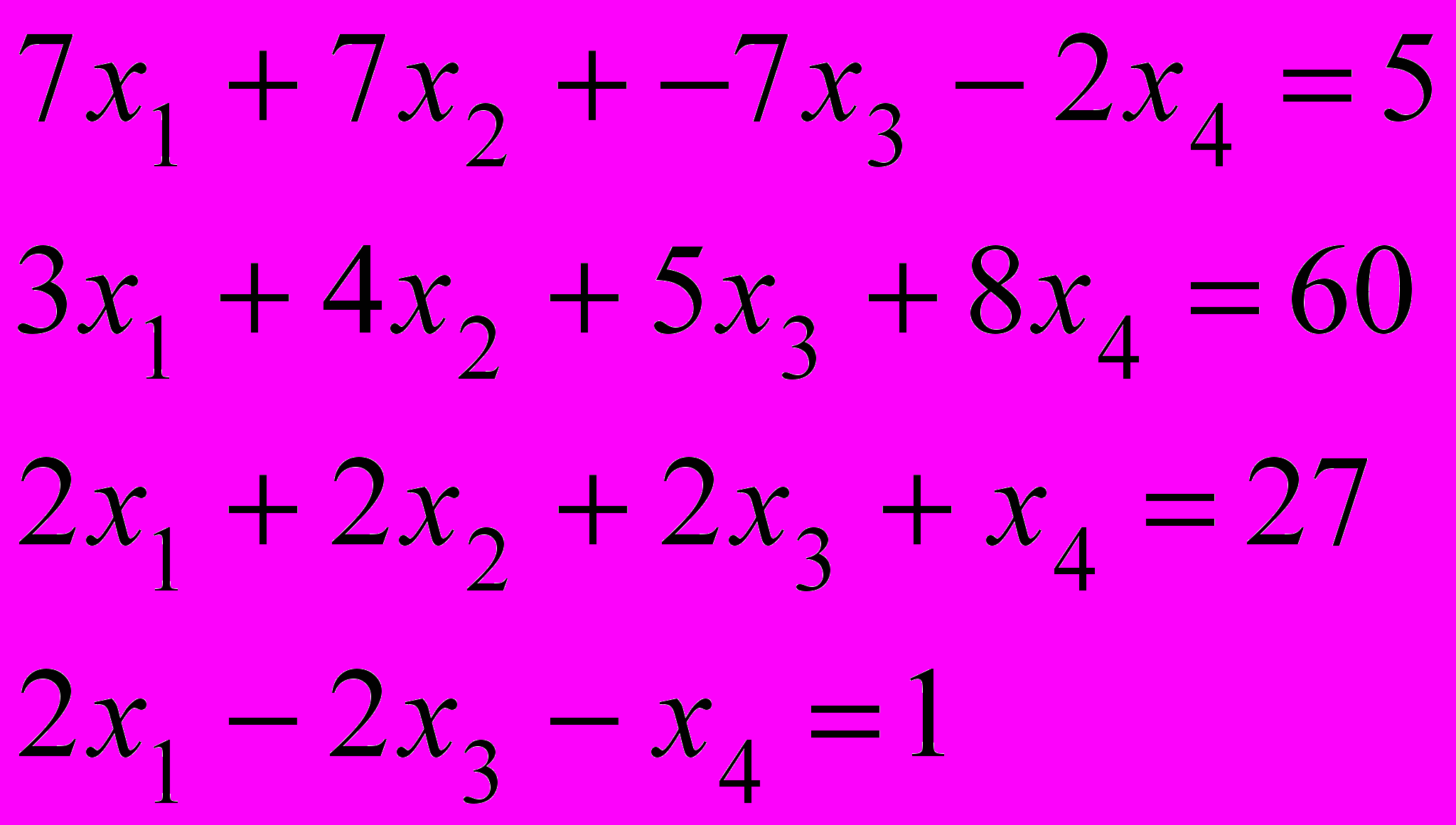
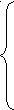2. Із двох заводів поставляється устаткування для двох підприємств, потреби яких відповідно 200 й 300 одиниць устаткування. Перший завод випустив 350 одиниць устаткування, а другий – 150 одиниць устаткування. Витрати на перевезення устаткування із заводів на кожне підприємство задані таблицею:

Завод	Витрати на перевезення на підприємства, грош. од.
	Підприємство 1	Підприємство 2
Завод 1	15	20
Завод 2	8	25

Мінімальні витрати на перевезення дорівнюють 7950 грош. од. Знайти оптимальний план перевезення устаткування.

3. Матриця має вигляд:

0.52351	0.21173	0.4485	0
0.218742	0	0.12284	0.2354
0.02156	0.1	0.321154	0.155
0.236188	0.68827	0.107506	0.6096

4. Матриця витрат має вигляд:

0,242105263	0,114166	0,188256	0,2599232
0,471578947	0,169149	0,568797	0
0,632982456	0,041237	0,032239	0,237516
0,334736842	0,203513	0,120322	0,0422535

5. Матриця міжгалузевих зв’язків, вектор цін і обсяг кінцевої продукції:

x				p	Y
378	0	0	29	1,7	82
200	0	172	35	3,66	121
45	144	37	331	1,23	68
123	88	39	86	3,8	86

Варіант 17.

1.



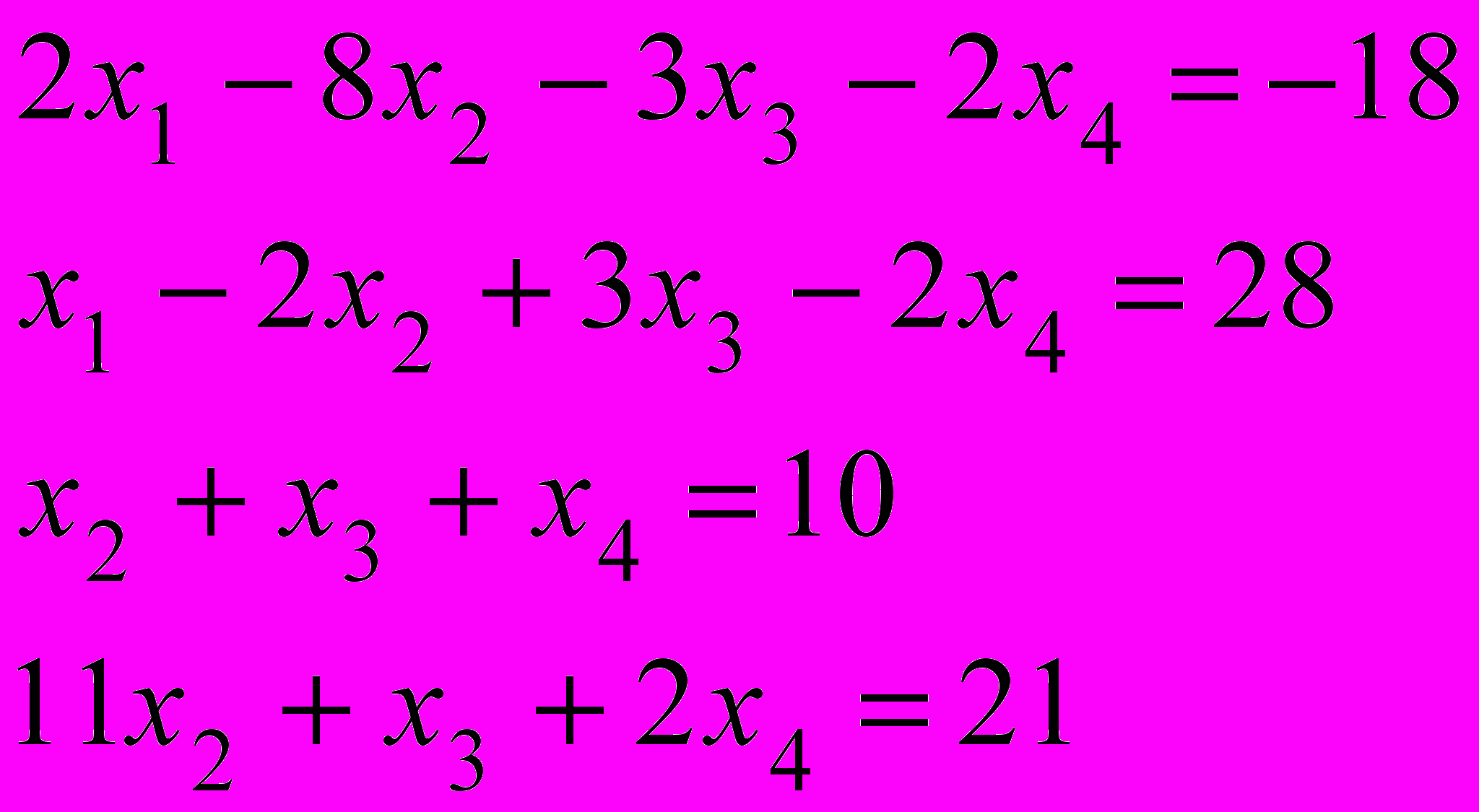
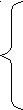
2. В економіці й господарській діяльності важливу роль відіграє припущення, що механізм ринкової конкуренції зрушує ціну на продукт настільки, що попит і пропозиція стають рівними одне одному. Припустімо, що функція попиту на холодильники для деякого періоду часу має вигляд: x1=12000–5x2, де x1 – ціна холодильника, а x2 – відповідна їх кількість. Нехай функція пропозиції має вигляд: x1=3000–x2. Визначити, за яких умов x1 і x2 настає рівновага? Розв’язати задачу матричним методом.


3. Матриця має вигляд:

0,1550	0	0,4485	0,236188
0	0,211730	0,321154	0,218742
0,2354	0,68827	0,12284	0,02156
0,6096	0,1	0,107506	0,52351

4. Матриця витрат має вигляд:

0,242105263	0,022508	0,021799	0,0043859
2,39196836	0,169149	0,334082	0
5,466334043	0,070209	0,032239	0,034611
19,83751141	2,377795	0,825706	0,0422535

5. Матриця міжгалузевих зв’язків, вектор цін і обсяг кінцевої продукції:

x				p	Y
266	67	63	137	0,54	177
191	488	106	49	0,99	106
77	251	81	0	9	89
49	17	33	188	23,4	280